Maya kalender

Maya -kalendern är ett system av kalendrar som används i förcolumbianska Mesoamerika och i många moderna samhällen i de guatemalanska högländerna, Veracruz , Oaxaca och Chiapas , Mexiko.

Det väsentliga i Maya-kalendern är baserad på ett system som hade varit i vanligt bruk i hela regionen, som går tillbaka till åtminstone 500-talet f.Kr. Den delar många aspekter med kalendrar som använts av andra tidigare mesoamerikanska civilisationer, såsom Zapotec och Olmec och samtida eller senare såsom de mixtekiska och aztekiska kalendrarna .

Av Maya-mytologiska traditionen, som dokumenterats i Colonial Yucatec-berättelser och rekonstruerade från senklassiska och postklassiska inskriptioner, tillskrivs gudomen Itzamna ofta för att föra kunskapen om det kalendriska systemet till de förfäders Maya, tillsammans med att skriva i allmänhet och andra grundläggande aspekter av Mayakultur.

Översikt

Ytterligare information: Maya astronomi

Mayakalendern består av flera cykler eller räkningar av olika längd. 260-dagarsräkningen är känd för forskare som Tzolkin eller Tzolk'in . Tzolkin kombinerades med ett 365-dagars vagt solår känt som Haab' för att bilda en synkroniserad cykel som varar i 52 Haab', kallad kalenderrundan . Kalenderrundan används fortfarande av många grupper i det guatemalanska höglandet.

En annan kalender användes för att spåra längre tidsperioder och för inskription av kalenderdatum (dvs. identifiera när en händelse inträffade i förhållande till andra). Detta är den långa räkningen . Det är ett antal dagar sedan en mytologisk utgångspunkt. Enligt korrelationen mellan Long Count och västerländska kalendrar som accepteras av den stora majoriteten av Maya-forskare (känd som Goodman-Martinez-Thompson, eller GMT, korrelation), är denna utgångspunkt likvärdig med den 11 augusti 3114 f.Kr. i proleptiken gregoriansk kalender eller 6 september, i den julianska kalendern (−3113 astronomisk). GMT-korrelationen valdes av John Eric Sydney Thompson 1935 på grundval av tidigare korrelationer av Joseph Goodman 1905 (11 augusti), Juan Martínez Hernández 1926 (12 augusti) och Thompson själv 1927 (13 augusti). Genom sin linjära natur kunde den långa räkningen utvidgas till att hänvisa till vilket datum som helst långt in i det förflutna eller framtiden. Denna kalender involverade användningen av ett positionsbeteckningssystem , där varje position betecknade en ökande multipel av antalet dagar. Mayas siffersystem var i huvudsak vigesimalt (dvs bas -20) och varje enhet av en given position representerade 20 gånger enheten för positionen som föregick den. Ett viktigt undantag gjordes för andra ordningens platsvärde, som istället representerade 18 × 20, eller 360 dagar, närmare solåret än 20 × 20 = 400 dagar. Långräkningens cykler är oberoende av solåret.

Många Maya Long Count-inskriptioner innehåller en tilläggsserie , som ger information om månfasen , numret på den nuvarande lunationen i en serie om sex och vilken av de nio nattens herrar regler.

Mindre vanliga eller dåligt förstådda cykler, kombinationer och kalenderförlopp spårades också. En 819-dagarsräkning intygas i några få inskriptioner. Upprepande uppsättningar av 9 dagar (se nedan "Nio herrar av natten") förknippade med olika grupper av gudar , djur och andra viktiga begrepp är också kända.

Tzolkʼin

Huvudartikel: Tzolkʼin

Tzolkʼin (i modern Maya- ortografi ; också vanligen skriven tzolkin ) är det namn som vanligtvis används av mayanistiska forskare för Maya Heliga Runda eller 260 - dagarskalendern. Ordet tzolkʼin är en neologism myntad i Yucatec Maya , för att betyda "räkning av dagar" (Coe 1992). De olika namnen på denna kalender som används av precolumbian Maya-folk diskuteras fortfarande av forskare. Den aztekiska kalendermotsvarigheten kallades Tōnalpōhualli , på Nahuatl -språket.

Tzolkʼin-kalendern kombinerar tjugo dagars namn med de tretton dagarna för att producera 260 unika dagar. Det används för att bestämma tidpunkten för religiösa och ceremoniella händelser och för spådom. Varje efterföljande dag numreras från 1 upp till 13 och börjar sedan igen vid 1. Separat från detta ges varje dag ett namn i följd från en lista med 20 dagnamn:

Tzolkʼin-kalender: namngivna dagar och tillhörande glyfer

Sekv. Num. 1	Dagens namn 2	Glyfexempel 3 _	1600-talet. Yucatec 4	Quiché	Rekonstruerad Classic Maya 5		Sekv. Num. 1	Dagens namn 2	Glyfexempel 3 _	1600-talet. Yucatec 4	Quiché	Rekonstruerad Classic Maya 5
01	Imix		Imix	Imox	Imix (?) / Haʼ (?)		11	Chuwen		Chuen	B'atz'	(okänd)
02	Ikʼ		Ik	Iqʼ	Ikʼ		12	Eb'		Eb	Eʼ	(okänd)
03	Akʼbʼal		Akbal	Aq'ab'al	Akʼbʼal (?)		13	B'en		Ben	Aj	C'klab
04	K'an		Kan	K'at	K'an (?)		14	Ix		Ix	Jag, Balam	Hej X (?)
05	Chikchan		Chicchan	Kan	(okänd)		15	Män		Män	Tzikin	(okänd)
06	Kimi		Cimi	Kame	Cham (?)		16	Kʼibʼ		Cib	Ajmaq	(okänd)
07	Manikʼ		Manik	Kej	Manichʼ (?)		17	Kab'an		Caban	Nej'j	Chabʼ (?)
08	Lamat		Lamat	Qʼanil	Ekʼ (?)		18	Etz'nab'		Etznab	Tijax	(okänd)
09	Muluk		Muluc	Toj	(okänd)		19	Kawak		Cauac	Kawoq	(okänd)
10	Ok		Oc	Tzʼiʼ	(okänd)		20	Ajaw		Ahau	Ajpu	Ajaw
ANMÄRKNINGAR: Sekvensnumret för den namngivna dagen i Tzolkʼin-kalendern Dagens namn, i den standardiserade och reviderade ortografin av Guatemalas Academia de Lenguas Mayas Ett exempel glyf ( logogram ) för den namngivna dagen. Observera att för de flesta av dessa finns flera olika former registrerade; de som visas här är typiska för snidade monumentala inskriptioner (dessa är " cartouche "-versioner) Dagens namn, som registrerats från 1500-talets Yucatec Maya- konton, främst Diego de Landa ; denna ortografi har (tills nyligen) använts flitigt I de flesta fall är det faktiska dagsnamnet som talades under den klassiska perioden (ca 200–900) då de flesta inskriptioner gjordes inte känt. De versioner som ges här (i Classic Maya , inskrifternas huvudspråk) är rekonstruerade på basis av fonologiska bevis, om sådana finns tillgängliga; ett '?' symbolen indikerar att rekonstruktionen är preliminär.

Vissa system startade räkningen med 1 Imix, följt av 2 Ikʼ, 3 Akʼbʼal, etc. upp till 13 Bʼen. Dagsnumren börjar sedan igen vid 1 medan den namngivna dagsekvensen fortsätter framåt, så nästa dag i sekvensen är 1 Ix, 2 Men, 3 Kʼibʼ, 4 Kabʼan, 5 Etzʼnabʼ, 6 Kawak och 7 Ajaw. Med alla tjugo namngivna dagar använda började dessa nu upprepa cykeln medan nummersekvensen fortsätter, så nästa dag efter 7 är Ajaw 8 Imix. Upprepningen av dessa sammankopplade 13- och 20-dagarscykler tar därför 260 dagar att slutföra (det vill säga för varje möjlig kombination av nummer/namngiven dag att inträffa en gång).

Den tidigaste kända inskriptionen med en Tzolkʼin är en olmekisk öronspole med 2 Ahau 3 Ceh - 6.3.10.9.0, 2 september -678 (Julian astronomisk).

Haabʼ

Haab' månader : namn och glyfer i följd

Sekv. Num.	Yucatec namn	Hieroglyf	Klassisk period glyph tecken	Betydelsen av glyph	Rekonstruerad klassisk Maya
1	Pop			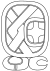	k'anjalaw
2	Woʼ				ik'at
3	Smutta				chakat
4	Sotz'			fladdermus	sotz'
5	Sek				kaseew
6	Xul				chikin
7	Yaxkʼin			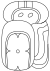	yaxk'in
8	Mol			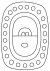	mol
9	Chʼen			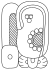svart	jag'siho'm
10	Yax			grön	yaxsiho'm
11	Sak			vit	saksiho'm
12	Keh			röd	chaksiho'm
13	Mak				mak
14	K'ank'in				uniiw
15	Muwan				muwaan
16	Pax				paxiil
17	Kʼayab			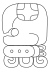	k'anasiiy
18	Kumkʼu			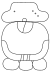	ohl
19	Wayebʼ			fem olyckliga dagar	wayhaab

Huvudartikel: Haabʼ

Haab'en bestod av arton månader om tjugo dagar vardera plus en period på fem dagar ("namnlösa dagar") i slutet av året, känt som Wayeb' (eller Uayeb i 1500-talets ortografi). Wayebs fem dagar ansågs vara en farlig tid. Foster (2002) skriver: "Under Wayeb upplöstes portaler mellan dödsriket och underjorden. Inga gränser hindrade de illvilliga gudarna från att orsaka katastrofer." För att avvärja dessa onda andar hade Maya seder och ritualer de utövade under Wayebʼ. Till exempel undvek människor att lämna sina hus och tvätta eller kamma håret. Bricker (1982) uppskattar att Haab' först användes omkring 550 f.Kr. med startpunkten för vintersolståndet .

Haabs månadsnamn är idag kända av sina motsvarande namn i kolonialtidens Yukatek Maya , som transkriberats av källor från 1500-talet (särskilt Diego de Landa och böcker som Chilam Balam från Chumayel). Fonemiska analyser av Haabs glyfnamn i pre-columbianska Maya-inskriptioner har visat att namnen för dessa tjugodagarsperioder varierade avsevärt från region till region och från period till period, vilket återspeglar skillnader i basspråk och användning i klassisk och Postklassiska epoker som föregick deras inspelning av spanska källor.

Varje dag i Haabs kalender identifierades med ett dagnummer i månaden följt av månadens namn. Dagssiffror började med en glyf översatt som "platsen för" en namngiven månad, vilket vanligtvis betraktas som dag 0 i den månaden, även om en minoritet behandlar det som dag 20 i månaden före den namngivna månaden. I det senare fallet är Pops sittande dag 5 av Wayebʼ. För majoriteten var årets första dag 0 Pop (Pops plats). Detta följdes av 1 Pop, 2 Pop så långt som 19 Pop sedan 0 Wo, 1 Wo och så vidare.

Eftersom Haabʼ hade 365 dagar och det tropiska året är 365,2422 dagar, sammanföll inte Haabʼs dagar med det tropiska året.

Kalenderrunda

Ett kalenderrundadatum är ett datum som ger både Tzolkʼin och Haabʼ. Detta datum kommer att upprepas efter 52 Haab' år eller 18 980 dagar, en kalenderrunda. Till exempel började den nuvarande skapandet på 4 Ahau 8 Kumkʼu. När detta datum återkommer kallas det för en kalenderrunda.

Aritmetiskt är varaktigheten av kalenderrundan den minsta gemensamma multipeln av 260 och 365; 18 980 är 73 × 260 Tzolk'in-dagar och 52 × 365 Haab'-dagar.

Inte alla möjliga kombinationer av Tzolkʼin och Haabʼ kan förekomma. För Tzolkʼin-dagarna Imix, Kimi, Chuwen och Kibʼ kan Haabʼ-dagen bara vara 4, 9, 14 eller 19; för Ikʼ, Manikʼ, Ebʼ och Kabʼan kan Haabʼ-dagen endast vara 0, 5, 10 eller 15; för Akbʼalʼ, Lamat, Bʼen och Etzʼnabʼ kan Haabʼ-dagen endast vara 1, 6, 11 eller 16; för K'an, Muluk, Ix och Kawak kan Haab'-dagen bara vara 2, 7, 12 eller 17; och för Chikchan, Ok, Men och Ajaw kan Haab'-dagen bara vara 3, 8, 13 eller 18.

Årsbärare

     En "Årsbärare" är ett Tzolkʼin -dagsnamn som förekommer på 0 Pop, Haabʼs första dag . Eftersom det finns 20 Tzolkʼin-dagnamn, 365 dagar i Haabʼ, och resten av 365 dividerat med 20 är 5 ( 365 = 18×20 + 5 ), kommer Tzolkʼin-dagsnamnet för varje på varandra följande 0 Pop att vara 5 senare i cykeln av Tzolk'in-dagens namn. På samma sätt, eftersom det finns 13 Tzolk'in-dagar, och resten av 365 dividerat med 13 är 1 ( 365 = 28×13 + 1 ), kommer Tzolk'in-dagtalet för varje på varandra följande 0 Pop att vara 1 större än tidigare. Som sådan är sekvensen av Tzolk'in-datum som motsvarar Haab'-datum 0 Pop följande:

• 1 Ikʼ
• 2 Manikʼ
• 3 Ebʼ
• 4 Kabʼan
• 5 Ikʼ
• ...
• 19 Eb'
• 20 Kab'an
• 1 Ik'
• ...

Årsbärarna är alltså de fyra Tzolk'in-dagsnamnen som förekommer i denna sekvens: Ik', Manik', Eb' och Kab'an.

"Year Bearer" översätter bokstavligen ett mayakoncept. Dess betydelse ligger i två fakta. För det första är de fyra åren som leds av Årsbärarna uppkallade efter dem och delar deras egenskaper; därför har de också sina egna prognostikationer och skyddsgudar. Dessutom, eftersom årsbärarna är geografiskt identifierade med gränsmarkörer eller berg, hjälper de till att definiera det lokala samhället.

Det klassiska systemet med årbärare som beskrivs ovan finns i Tikal och i Dresden Codex . Under den sena klassiska perioden användes en annan uppsättning årbärare i Campeche. I detta system var årsbärarna Tzolkʼin som sammanföll med 1 Pop. Dessa var Ak'b'al, Lamat, B'en och Edznab. Under den post-klassiska perioden i Yucatán var ett tredje system i bruk. I detta system var årbärarna de dagar som sammanföll med 2 Pop: K'an, Muluc, Ix och Kawak. Detta system finns i Chronicle of Oxkutzcab. Dessutom, precis innan den spanska erövringen i Mayapan började Maya att räkna Haabʼs dagar från 1 till 20. I detta system är årsbärarna desamma som i 1 Pop – Campeche-systemet. Classic Year Bearer-systemet används fortfarande i det guatemalanska höglandet och i Veracruz, Oaxaca och Chiapas, Mexiko.

Lång räkning

Östra sidan av Stela C, Quirigua med det mytiska skapelsedatumet för 13 baktuns, 0 katuns, 0 tuns, 0 uinals, 0 kins, 4 Ahau, 8 Cumku – 11 augusti 3114 f.Kr. i den proleptiska gregorianska kalendern

Huvudartikel: Mesoamerican Long Count-kalender

Eftersom kalenderrunda datum upprepas var 18 980:e dag, ungefär 52 solår, upprepas cykeln ungefär en gång varje livstid, så en mer förfinad dateringsmetod behövdes om historien skulle registreras korrekt. För att ange datum över perioder längre än 52 år använde mesoamerikaner Long Count-kalendern.

Mayanamnet för en dag var kʼin . Tjugo av dessa kʼiner är kända som en winal eller uinal . Arton winals gör en tun . Tjugo tuns är kända som en k'atun . Tjugo kʼatuns gör en bʼakʼtun .

The Long Count-kalendern identifierar ett datum genom att räkna antalet dagar från Mayas skapelsedatum 4 Ahaw, 8 Kumkʼu (11 augusti 3114 f.Kr. i den proleptiska gregorianska kalendern eller 6 september i den julianska kalendern -3113 astronomisk datering). Men istället för att använda ett bas-10-schema ( decimal ) räknades Långräkningsdagarna i ett modifierat bas-20-schema. Således är 0.0.0.1.5 lika med 25 och 0.0.0.2.0 är lika med 40. Eftersom vinstenheten återställs efter att endast räknat till 18, använder Long Count konsekvent bas-20 endast om tunen anses vara den primära enheten för mätning, inte kʼin; där kʼin- och winal-enheterna är antalet dagar i tun. Long Count 0.0.1.0.0 representerar 360 dagar, snarare än 400 i ett rent bas-20 ( vigesimalt ) antal.

Det finns också fyra sällan använda högre ordningscykler: piktun , kalabtun , kʼinchiltun och alautun .

Eftersom de långa grevens datum är entydiga var den långa greven särskilt väl lämpad att använda på monument. De monumentala inskriptionerna skulle inte bara inkludera de 5 siffrorna i den långa greven, utan skulle också inkludera de två tzolkʼin-tecken följt av de två haabʼ-tecken.

Feltolkning av den mesoamerikanska långräkningskalendern var grunden för en populär tro att en katastrof skulle äga rum den 21 december 2012 . Den 21 december 2012 var helt enkelt dagen då kalendern gick till nästa bʼakʼtun , vid Long Count 13.0.0.0.0. Datumet för starten av nästa b'ak'tun (Long Count 14.0.0.0.0) är den 26 mars 2407. Datumet för starten av nästa piktun (en komplett serie av 20 b'ak'tuns), vid Long Count 1.0 .0.0.0.0, är ​​13 oktober 4772.

Tabell över långa räkningsenheter

Long Count enhet	Lång räkningsperiod	dagar	Ungefärliga solår
1 Kʼin		1
1 Winal	20 Kʼin	20
1 Tun	18 Winal	360	1
1 K'atun	20 Tun	7 200	20
1 Bʼakʼtun	20 K'atun	144 000	394
1 Piktun	20 Bʼakʼtun	2 880 000	7,885
1 Kalabtun	20 Piktun	57 600 000	157,704
1 Kʼinchiltun	20 Kalabtun	1 152 000 000	3,154,071
1 Alautun	20 Kʼinchiltun	23 040 000 000	63,081,429

Kompletterande serie

Många klassiska periodinskriptioner inkluderar en serie glyfer som kallas tilläggsserien. Funktionen av denna serie utarbetades till stor del av John E. Teeple . Tilläggsserien består oftast av följande element:

Nattens herrar

Huvudartikel: Lords of the Night

Varje natt styrdes av en av underjordens nio herrar. Denna niodagarscykel skrevs vanligtvis som två glyfer: en glyf som refererade till de nio herrarna som en grupp, följt av en glyf för den herre som skulle härska nästa natt.

Lunar-serien

En månserie skrivs i allmänhet som fem glyfer som ger information om den aktuella månen , numret på månen i en serie om sex, den nuvarande härskande månguden och längden på den nuvarande månens mån.

Månens ålder

Mayan räknade antalet dagar i den nuvarande lunationen. De använde två system för nolldatumet för måncykeln: antingen första natten kunde de se den tunna halvmånen eller första morgonen när de inte kunde se den avtagande månen. Månens ålder avbildades av en uppsättning glyfer som mayanister myntade glyferna D och E:

• En nymåneglyph användes för dag noll i måncykeln.
• D-glyfer användes för månålder för dag 1 till 19, med antalet dagar som hade gått från nymånen.
• För månåldern 20 till 30 användes en E-glyph, med antalet dagar från 20.

Count of Lations

Mayan räknade lunationerna. Denna cykel visas i månserien som två glyfer som moderna forskare kallar "C" och "X" glyferna. C-glyfen kan föregås med ett nummer som indikerar lunationen. Inget prefix betydde en, medan siffrorna två till sex angav de andra lunationerna. Det fanns också en del av C-glyfen som indikerade var detta föll i en större cykel av 18 lunationer. Till C-glyfen fanns "X"-glyfen som visade ett liknande mönster av 18 lunationer.

Lunationslängd

nuvarande erans månsynodiska period är cirka 29,5305877 _{medelsoldagar} eller cirka 29 dagar 12 timmar 44 minuter och 2+ ^7/9 sekunder. Som ett heltal kommer antalet dagar per lunation att vara antingen 29 eller 30 dagar, där 30-dagarsintervallen nödvändigtvis inträffar något oftare än 29-dagarsintervallen. Maya skrev om månmånaden var 29 eller 30 dagar som två glyfer: en glyf för lunation längd följt av antingen en glyf som består av en mån glyf över en bunt med suffixet 9 för en 29-dagars lunation eller en mån glyf med suffixet 10 för en 30-dagars lunation. Eftersom Maya inte använde bråk, uppskattades lunationer genom att använda formeln att det fanns 149 lunationer som slutfördes på 4400 dagar, vilket gav en ganska kort medelmånad på exakt 4400 / 149 = 29+ 79 ^/ 149 _dagar = ²⁹ dagar ₁₂ timmar 43 minuter och 29+ ⁵⁹ / ₁₄₉ sekunder, eller cirka 29,5302 dagar.

819 dagar

Vissa Maya-monument inkluderar glyfer som registrerar en räkning på 819 dagar i deras inledande serie. Dessa kan också hittas i Dresden codex . Detta beskrivs i Thompson. Fler exempel på detta finns i Kelley. Varje grupp på 819 dagar var associerad med en av fyra färger och den kardinalriktning som den var associerad med – svart motsvarade väst, rött mot öst, vitt mot norr och gult mot söder.

Antalet 819 dagar kan beskrivas på flera sätt: De flesta av dessa hänvisas till med en "Y"-glyph och ett nummer. Många har också en glyf för Kʼawill – guden med en rykande spegel i huvudet. K'awill har föreslagits ha en länk till Jupiter. I Dresden codex almanacka 59 finns Chaacs av ​​de fyra färgerna. De medföljande texterna börjar med en riktningsglyf och ett verb för 819-dagars-fraser. Anderson ger en detaljerad beskrivning av antalet 819 dagar.

Kort räkning

  Under den sena klassiska perioden började Maya att använda en förkortad kort räkning istället för den långa räkningen. Ett exempel på detta finns på altare 14 i Tikal. I kungadömena i det postklassiska Yucatán användes den korta räkningen istället för den långa räkningen. Den cykliska Short Count är en räkning av 13 kʼatuns (eller 260 tuns), där varje kʼatun fick sitt namn efter sin avslutande dag, Ahau ('Herre'). 1 Imix valdes som den återkommande "första dagen" i cykeln, motsvarande 1 Cipactli i antalet aztekiska dagar. Cykeln räknades från katun 11 Ahau till katun 13 Ahau. Eftersom en katun är 20 × 360 = 7200 dagar lång, och resten av 7200 dividerat med 13 är 11 ( 7200 = 553×13 + 11 ), är dagnumret för den avslutande dagen för varje efterföljande katun 9 större än tidigare (omslag) runt vid 13, eftersom endast 13 dagars nummer används). Det vill säga att börja med katunen som börjar med 1 Imix, är sekvensen av avslutande dagnummer 11, 9, 7, 5, 3, 1, 12, 10, 8, 6, 4, 2, 13, 11, .. ., alla med namnet Ahau. Den avslutande dag 13 Ahau följdes av återinträdet första dag 1 Imix. Detta är systemet som finns i Chilam Balams koloniala böcker . På karakteristiskt mesoamerikanskt sätt projicerar dessa böcker cykeln på landskapet, med 13 Ahauob "Lordships" som delar upp landet Yucatán i 13 "riken".

Se även

• 2012 års fenomen
• Maya religion
• Mayanism
• Tres Zapotes#Stela C
• Maya astronomi
• Aztekisk kalender

Anteckningar

•    Aveni, Anthony F. (2001). Skywatchers (ursprungligen publicerad som: Skywatchers of Ancient Mexico [1980], reviderad och uppdaterad utgåva). Austin: University of Texas Press . ISBN 0-292-70504-2 . OCLC 45195586 .
• Boot, Erik (2002). En preliminär klassisk Maya-engelska/engelska-klassiska Maya-vokabulär för hieroglyfiska läsningar ( PDF) . Mesoweb . Hämtad 2006-11-10 .
•     Bricker, Victoria R. (februari 1982). "Ursprunget till Mayas solkalender". Aktuell antropologi . Chicago, IL: University of Chicago Press , sponsrad av Wenner-Gren Foundation for Anthropological Research . 23 (1): 101–103. doi : 10.1086/202782 . ISSN 0011-3204 . OCLC 62217742 . S2CID 143962107 .
•   Chambers, David Wade (1965). "Kände Maya den metoniska cykeln". Isis . 56 (3): 348–351. doi : 10.1086/350004 . S2CID 145711182 .
•   Coe, Michael D. (1965). "En modell av forntida Maya-gemenskapsstruktur i Maya-låglandet". Southwestern Journal of Anthropology . 21 . doi : 10.1086/soutjanth.21.2.3629386 . S2CID 130245359 .
•    Coe, Michael D. (1987). Maya (4:e reviderade upplagan). London och New York: Thames & Hudson . ISBN 0-500-27455-X . OCLC 15895415 .
•    Coe, Michael D. (1992). Att bryta Mayakoden . London: Thames & Hudson . ISBN 0-500-05061-9 . OCLC 26605966 .
•    Foster, Lynn V. (2002). Handbok till livet i den antika Mayavärlden . med förord ​​av Peter Mathews. New York: Fakta om filen . ISBN 0-8160-4148-2 . OCLC 50676955 .
•    Ivanoff, Pierre (1971). Mayan Enigma: The Search for a Lost Civilization . Elaine P. Halperin (översättning) (översättning av Découvertes chez les Mayas , engelsk upplaga). New York: Delacorte Press. ISBN 0-440-05528-8 . OCLC 150172 .
•   Jones, Christopher (1984). Dechiffrera Maya-hieroglyfer . Carl P. Beetz (illus.) (förberedd för Weekend Workshop 7 och 8 april 1984, 2:a uppl.). Philadelphia: University Museum, University of Pennsylvania . OCLC 11641566 .
• Kettunen, Harri; Christophe Helmke (2020). Introduktion till Maya-hieroglyfer: 17:e upplagan (PDF) . Couvin, Belgien: Wayeb . Hämtad 2020-10-06 .
• Linden, John H. (1996). Deity Head-varianter av C Glyph . The Eight Palenque Round Table, 1993. s. 343–356.
•   MacDonald, G. Jeffrey (27 mars 2007). "Förutspår Maya-kalendern 2012 års apokalyps?" . USA idag . McLean, VA: Gannett Company . ISSN 0734-7456 . Arkiverad från originalet 2008-03-16 . Hämtad 2009-05-28 .
•    Milbrath, Susan (1999). Star Gods of the Maya: Astronomy in Art, Folklore, and Calendars . Linda Schele-serien i Maya och förcolumbianska studier. Austin: University of Texas Press . ISBN 0-292-75225-3 . OCLC 40848420 .
•    Miller, Mary ; Karl Taube (1993). Gudarna och symbolerna för det antika Mexiko och Maya: En illustrerad ordbok över mesoamerikansk religion . London: Thames och Hudson. ISBN 0-500-05068-6 . OCLC 27667317 .
• Rice, Prudence M., Maya Calendar Origins: Monuments, Mythistory, and the Materialization of Time (Austin, TX: University of Texas Press, 2007).
•    Robinson, Andrew (2000). Berättelsen om att skriva: Alfabet, hieroglyfer och piktogram . London och New York: Thames & Hudson . ISBN 0-500-28156-4 . OCLC 59432784 .
• Roys, Ralph L. (1967). Boken av Chilam Balam av Chumayel . Norman: University of Oklahoma Press .
•    Schele, Linda ; David Freidel (1992). A Forest of Kings: The Untold Story of the Ancient Maya (ursprungligen publicerad New York: Morrow, 1990, pbk reprint ed.). New York: Harper Perennial . ISBN 0-688-11204-8 . OCLC 145324300 .
• Schele, Linda; Nickolai Grube; Federico Fahsen (oktober 1992). "Lunar Series in Classic Maya Inscriptions: New Observation and Interpretations". Texas Notes on Precolumbian Art, Writing and Culture (29).
•    Tedlock, Barbara (1992). Time and the Highland Maya (rev. red.). Albuquerque: University of New Mexico Press . ISBN 0-8263-0577-6 . OCLC 7653289 .
• Teeple, John E. (november 1931). "Maya Astronomy" (PDF) . Bidrag till amerikansk arkeologi . Vol. I (Pub. 403 uppl.). Washington DC: Carnegie Institution of Washington. s. 29–116.
•    Tedlock, Dennis , red. (1985). Popol Vuh: Den definitiva utgåvan av Mayaboken om livets gryning och gudarnas och kungens härlighet . Översatt av Tedlock, Dennis. med kommentarer baserade på den gamla kunskapen om den moderna Quiché Maya. New York: Simon & Schuster . ISBN 0-671-45241-X . OCLC 11467786 .
•   Thomas, Cyrus (1897). "Dagsymboler för Mayaåret" . I JW Powell (red.). Sextonde årsrapporten från Bureau of American Ethnology till Secretary of the Smithsonian Institution, 1894–1895 ( E-bok onlinereproduktion). Washington DC: Bureau of American Ethnology , Smithsonian Institution ; US Government Printing Office . s. 199–266. OCLC 14963920 . Arkiverad från originalet den 22 januari 2007 – via Project Gutenberg .
•    Thompson, J. Eric S. (1971). Maya Hieroglyphic Writing: An Introduction, 3:e upplagan . Civilization of the American Indian Series, nr 56 (3:e upplagan). Norman: University of Oklahoma Press . ISBN 0-8061-0447-3 . OCLC 275252 .
•   Tozzer, Alfred M. , red. (1941). Landas Relación de las cosas de Yucatán: en översättning . Papers of the Peabody Museum of American Archaeology and Ethnology, Harvard University vol. 18. Översatt av Tozzer, Alfred M. Charles P. Bowditch och Ralph L. Roys (ytterligare översättning) (översättning av Diego de Landas Relación de las cosas de Yucatán [original ca 1566], med anteckningar, kommentarer och bilagor som innehåller översatta utdrag av verk av Gaspar Antonio Chi , Tomás López Medel, Francisco Cervantes de Salazar och Antonio de Herrera y Tordesillas . Engelska red.). Cambridge, MA: Peabody Museum of Archaeology and Ethnology . OCLC 625693 .
•    Voss, Alexander (2006). "Astronomi och matematik". I Nikolai Grube (red.). Maya: Divine Kings of the Rain Forest . Eva Eggebrecht och Matthias Seidel (assistentred.). Köln, Tyskland: Könemann. s. 130–143. ISBN 978-3-8331-1957-6 . OCLC 71165439 .

externa länkar

• Dagsymboler för Mayaåret vid Project Gutenberg 1897 text av Cyrus Thomas
• datumomvandlare på FAMSI Denna omvandlare använder den julianska/gregorianska kalendern och inkluderar 819 dagars cykel och månålder.
• Interaktiva Maya-kalendrar