Mesoamerikansk långräkningskalender

Östra sidan av stela C, Quirigua med det mytiska skapelsedatumet för 13 baktuns , 0 katuns, 0 tuns, 0 uinals, 0 kins, 4 Ahau 8 Cumku – 11 augusti 3114 f.Kr. i den proleptiska gregorianska kalendern .

Mesoamerican Long Count-kalendern är en icke-repeterande bas-20- och bas-18-kalender som används av flera förcolumbianska mesoamerikanska kulturer, särskilt Maya . Av denna anledning är den ofta känd som Maya Long Count-kalendern . Med hjälp av en modifierad vigesimal räkning identifierar Long Count-kalendern en dag genom att räkna antalet dagar som gått sedan ett mytiskt skapelsedatum som motsvarar den 11 augusti 3114 f.Kr. i den proleptiska gregorianska kalendern . The Long Count-kalendern användes flitigt på monument.

Bakgrund

De två mest använda kalendrarna i det precolumbianska Mesoamerika var 260-dagars Tzolkʼin och 365-dagars Haabʼ . Motsvarande aztekiska kalendrar är kända i Nahuatl som Tonalpohualli och Xiuhpohualli .

Kombinationen av ett Haabʼ och ett Tzolkʼin-datum identifierar en dag i en kombination som inte inträffar igen på 18 980 dagar (52 Haabʼ-cykler på 365 dagar motsvarar 73 Tzolkʼin-cykler på 260 dagar, ungefär 52 år), en period som kallas kalenderrundan . För att identifiera dagar över perioder längre än detta använde mesoamerikaner Long Count-kalendern.

Långa räkningsperioder

Detalj som visar kolumner med glyfer från en del av 200-talet e.Kr. La Mojarra Stela 1 . Den vänstra kolumnen visar ett Long Count-datum 8.5.16.9.7, eller 156 e.Kr. De andra synliga kolumnerna är glyfer från Epi-Olmec-skriptet .

Långräkningskalendern identifierar ett datum genom att räkna antalet dagar från ett startdatum som i allmänhet beräknas vara 11 augusti 3114 f.Kr. i den proleptiska gregorianska kalendern eller 6 september i den julianska kalendern (eller -3113 i astronomisk årsnumrering). Det har varit mycket debatt om den exakta korrelationen mellan de västerländska kalendrarna och de långa räkningskalendrarna. Datumet 11 augusti är baserat på GMT-korrelationen.

Fullbordandet av 13 b'ak'tuns (11 augusti 3114 fvt) markerar skapandet av människors värld enligt Maya. Den här dagen orsakade Upphöjd-Himmel-Lord tre stenar som sattes av tillhörande gudar på Ligg-Ned-Himmel, Första-Tre-Sten-Place. Eftersom himlen fortfarande låg på urhavet var den svart. Inställningen av de tre stenarna centrerade kosmos som gjorde att himlen kunde höjas och avslöja solen .

Istället för att använda ett bas 10-schema räknades Long Count-dagarna i ett modifierat bas-20-schema. I ett rent bas 20-schema är 0.0.0.1.5 lika med 25 och 0.0.0.2.0 är lika med 40. Den långa räkningen är dock inte ren bas-20, eftersom den andra siffran från höger (och bara det) siffra) rullar över till noll när den når 18. [ citat behövs ] Således representerar 0.0.1.0.0 inte 400 dagar, utan snarare bara 360 dagar och 0.0.0.17.19 representerar 359 dagar.

Namnet bʼakʼtun uppfanns av moderna forskare. Den numrerade långa greven var inte längre i bruk när spanjorerna anlände till Yucatánhalvön, även om onumrerade k'atuns och tuns fortfarande var i bruk. Istället använde Maya en förkortad Short Count .

Tabell över långa räkningsenheter

Long Count enhet
Lång räkningsperiod 		dagar
Ungefärliga solår
1 Kʼin   1  
1 Winal 20 Kʼin 20  
1 Tun 18 Winal 360 1
1 K'atun 20 Tun 7 200 20
1 Bʼakʼtun 20 K'atun 144 000 394
1 Piktun 20 Bʼakʼtun 2 880 000 7,885
1 Kalabtun 20 Piktun 57 600 000 157,704
1 Kʼinchiltun 20 Kalabtun 1 152 000 000 3,154,071
1 Alautun 20 Kʼinchiltun 23 040 000 000 63,081,429
1 Hablatun 20 Alautun 460 800 000 000 1,261,628,585

Mesoamerikanska siffror

Maya siffror

Long Count-datum skrivs med mesoamerikanska siffror, som visas i den här tabellen. En punkt representerar 1 medan en stapel är lika med 5 . Skalglyfen användes för att representera nollkonceptet. The Long Count-kalendern krävde användningen av noll som platshållare och presenterar en av de tidigaste användningarna av nollbegreppet i historien .

På Maya-monument är Long Count-syntaxen mer komplex. Datumsekvensen ges en gång, i början av inskriptionen och inleds med den så kallade ISIG (Introductory Series Initial Glyph) som läser tzik-a(h) habʼ [beskyddare av Haabʼ månad] (" vördad var årsräkningen med beskyddaren [månadens]"). Därefter kommer de 5 siffrorna i den långa räkningen, följt av kalenderrundan (tzolkʼin och Haabʼ) och kompletterande serier . Tilläggsserien är valfri och innehåller måndata, till exempel månens ålder på dagen och den beräknade längden på den aktuella månen . Texten fortsätter sedan med vilken aktivitet som helst som inträffade det datumet.

En ritning av en fullständig Maya Long Count-inskription visas nedan .

Tidigast långa räkningar

Den tidigaste samtida Long Count-inskriften som hittills upptäckts finns på Stela 2 i Chiapa de Corzo , Chiapas , Mexiko, och visar ett datum på 36 f.Kr., även om Stela 2 från Takalik Abaj , Guatemala kan vara tidigare. [1] Takalik Abaj Stela 2:s mycket misshandlade Long Count-inskription visar 7 bak'tuns , följt av k'atuns med en preliminär 6-koefficient, men det kan också vara 11 eller 16, vilket ger intervallet för möjliga datum att falla mellan 236 och 19 f.Kr. [ citat behövs ]

Även om Takalik Abaj Stela 2 förblir kontroversiell, inkluderar denna tabell den, såväl som sex andra artefakter med de åtta äldsta Long Count-inskriptionerna enligt Dartmouth-professorn Vincent H. Malmström (två av artefakterna innehåller två datum och Malmström inkluderar inte Takalik Abaj Stela 2). Tolkningen av inskriptioner på vissa artefakter skiljer sig åt.

Arkeologisk utgrävning namn gregoriansk datum

GMT (584283) korrelation

Lång räkning Plats
Takalik Abaj Stela 2 236 – 19 f.Kr 7.(6,11,16).?.?.? Retalhuleu , Guatemala
Chiapa de Corzo Stela 2
6 december 36 f.Kr. eller 9 oktober 182 e.Kr
7.16.3.2.13 eller 8.7.3.2.13 		Chiapas, Mexiko
Tres Zapotes Stela C 1 september 32 fvt 7.16.6.16.18 Veracruz , Mexiko
El Baúl Stela 1 11 - 37 e.Kr


7.18.9.7.12, 7.18.14.8.12, 7.19.7.8.12 eller 7.19.15.7.12 		Escuintla , Guatemala
Takalik Abaj Stela 5
31 augusti 83 e.Kr. eller 19 maj 103 e.Kr
8.2.2.10.15 eller 8.3.2.10.15 		Retalhuleu, Guatemala
Takalik Abaj Stela 5 3 juni 126 e.Kr 8.4.5.17.11 Retalhuleu, Guatemala
La Mojarra Stela 1 19 maj 143 e.Kr 8.5.3.3.5 Veracruz, Mexiko
La Mojarra Stela 1 11 juli 156 e.Kr 8.5.16.9.7 Veracruz, Mexiko
Nära La Mojarra Tuxtla statyett 12 mars 162 e.Kr 8.6.2.4.17 Veracruz, Mexiko

Av de sex platserna ligger tre i den västra kanten av Mayas hemland och tre ligger flera hundra kilometer längre västerut, vilket leder till att vissa forskare tror att Long Count-kalendern föregår Maya. La Mojarra Stela 1, Tuxtla-statyetten, Tres Zapotes Stela C och Chiapa Stela 2 är alla inskrivna i en Epi-Olmec , inte Maya-stil. El Baúl Stela 2, å andra sidan, skapades i Izapan -stil.

Den första otvetydiga Maya-artefakten är Stela 29 från Tikal , med Long Count-datumet 292 CE (8.12.14.8.15), mer än 300 år efter Stela 2 från Chiapa de Corzo.

På senare tid, med upptäckten i Guatemala av stenblockstexten San Bartolo ( omkring 300 f.Kr.), har det hävdats att den här texten firar ett kommande slutfirande för en period. Denna tidsperiod kan ha beräknats sluta någon gång mellan 7.3.0.0.0 och 7.5.0.0.0 - 295 respektive 256 f.Kr. Förutom att detta är den tidigaste Maya-hieroglyftexten som hittills avslöjats, skulle det utan tvekan vara det tidigaste glyfiska beviset hittills på Long Count-notation i Mesoamerika.

Korrelationer mellan västerländska kalendrar och den långa räkningen


Baksidan av Stela C från Tres Zapotes , en arkeologisk plats i Olmec. Detta är det näst äldsta Long Count-datumet som hittills upptäckts. Siffrorna 7.16.6.16.18 översätts till 1 september 32 fvt (gregorianska). Glyferna som omger datumet är vad som tros vara ett av de få bevarade exemplen på Epi-Olmec-manus .

Maya- och västerländska kalendrar är korrelerade genom att använda ett julianskt dagnummer (JDN) för startdatumet för den nuvarande skapelsen - 13.0.0.0.0, 4 Ajaw , 8 Kumkʼu. Detta kallas en "korrelationskonstant". Den allmänt accepterade korrelationskonstanten är den modifierade Thompson 2, " Goodman –Martinez- Thompson ", eller GMT-korrelationen på 584 283 dagar. Med hjälp av GMT-korrelationen började den nuvarande skapelsen den 6 september -3113 ( Juliansk astronomisk) - 11 augusti 3114 f.Kr. i den proleptiska gregorianska kalendern . Studiet av att korrelera Maya-kalendern och den västerländska kalendern kallas för korrelationsfrågan. GMT-korrelationen kallas även 11.16- korrelationen.

I Breaking the Maya Code skriver Michael D. Coe : "Trots oceaner av bläck som har spillts på ämnet, finns det nu inte den minsta chansen att dessa tre forskare (sammanblandade med GMT när man pratar om korrelationen) inte var höger ...". Bevisen för GMT-korrelationen är historiska, astronomiska och arkeologiska:

Historiskt : Kalenderrunda datum med ett motsvarande julianskt datum finns registrerade i Diego de Landas Relación de las cosas de Yucatán (skriven cirka 1566), Chronicle of Oxcutzkab och Chilam Balams böcker . De Landa spelar in ett datum som är en Tun som slutar i Short Count . Oxkutzcab innehåller 12 Tun-slut. Bricker och Bricker finner att endast GMT-korrelationen överensstämmer med dessa datum. Chilam Balams bok från Chumayel innehåller den enda koloniala hänvisningen till klassiska långräkningsdatum. Det julianska kalenderdatumet 11.16.0.0.0 (2 november 1539) bekräftar GMT-korrelationen.

The Annals of the Cakchiquels innehåller många Tzolkʼin-datum korrelerade med europeiska datum. Dessa bekräftar GMT-korrelationen. Weeks, Sachse och Prager transkriberade tre spådomskalendrar från höglandet Guatemala. De fann att 1772 års kalender bekräftar GMT-korrelationen. Fallet av Aztekrikets huvudstad Tenochtitlan inträffade den 13 augusti 1521. Ett antal olika krönikörer skrev att detta var en Tzolkʼin ( Tonalpohualli ) av 1 Snake.

Forskare efter erövringen som Sahagún och Durán registrerade Tonalpohualli- datum med ett kalenderdatum. Många inhemska samhällen i de mexikanska delstaterna Veracruz, Oaxaca och Chiapas och i Guatemala, främst de som talar mayaspråken Ixil, Mam, Pokomchí och Quiché, behåller Tzolkʼin och i många fall Haabʼ. Dessa överensstämmer alla med GMT-korrelationen. Munro Edmonsen studerade 60 mesoamerikanska kalendrar, varav 20 har kända korrelationer till europeiska kalendrar, och fann anmärkningsvärd överensstämmelse bland dem och att endast GMT-korrelationen passar de historiska, etnografiska och astronomiska bevisen.

Astronomisk : Varje korrekt korrelation måste matcha det astronomiska innehållet i klassiska inskriptioner. GMT-korrelationen gör ett utmärkt jobb med att matcha måndata i tilläggsserien . Till exempel: En inskription vid Solens tempel i Palenque registrerar att på Long Count 9.16.4.10.8 var det 26 dagar fullbordade i en 30 dagars lunation. Denna långa räkning är också inträdesdatumet för förmörkelsetabellen i Dresden Codex .

Med den tredje metoden (Palenque-systemet) skulle nymånen ha varit den första kvällen då man kunde se västerut efter solnedgången och se den tunna halvmånen. Med tanke på vår moderna förmåga att veta exakt var de ska leta, när halvmånen är fördelaktigt placerad, från en utmärkt plats, vid sällsynta tillfällen, med hjälp av en kikare eller ett teleskop, kan observatörer se och fotografera halvmånen mindre än en dag efter konjunktion. I allmänhet kan de flesta observatörer inte se nymånen med blotta ögat förrän den första kvällen när månfasdagen är minst 1,5. Om man antar att nymånen är den första dagen då månfasdagen är minst 1,5 klockan sex på kvällen i tidszonen UTC−6 (tidszonen i Mayaområdet) kommer GMT-korrelationen att matcha många måninskriptioner exakt. I det här exemplet var månfasdagen 27,7 (26 dagar räknat från noll) kl. 18.00 efter en konjunktion kl. 01.25 den 10 oktober 755 och en nymåne när månfasdagen var 1.7 kl. 18.00 den 11 oktober 755 (Juliansk kalender). Detta fungerar bra för många men inte alla måninskriptioner.

Moderna astronomer hänvisar till konjunktionen mellan solen och månen (den tid då solen och månen har samma ekliptiska longitud) som nymånen. Mesoamerikansk astronomi var observationsmässig inte teoretisk. Befolkningen i Mesoamerika visste inte om kopernikanska natur - de hade ingen teoretisk förståelse av himmelkropparnas orbitala natur. Vissa författare analyserar månens inskriptioner baserat på denna moderna förståelse av månens rörelser, men det finns inga bevis för att mesoamerikanerna gjorde det.

Den första metoden verkar ha använts för andra inskriptioner som Quirgua stela E (9.17.0.0.0). Med den tredje metoden bör den ha en månålder på 26 dagar när den faktiskt registrerar en nymåne. Om man använder GMT-korrelationen klockan sex på morgonen i tidszon -6, skulle detta vara 2,25 dagar före konjunktion, så det kunde registrera den första dagen då man inte kunde se den avtagande månen.

Fuls analyserade dessa inskriptioner och fann starka bevis för Palenque-systemet och GMT-korrelationen, men han varnade: "Analys av Lunar Series visar att minst två olika metoder och formler användes för att beräkna månens ålder och position i sexmånaderscykeln ..." som ger förmörkelsesäsonger när månen är nära sin uppåtgående eller nedåtgående nod och en förmörkelse sannolikt kommer att inträffa. Datum konverterade med hjälp av GMT-korrelationen överensstämmer nära med Dresden Codex-förmörkelsetabellerna. Dresden Codex innehåller en Venus- tabell som registrerar de heliakala uppgångarna av Venus. Med hjälp av GMT-korrelationen överensstämmer dessa nära med moderna astronomiska beräkningar.

Arkeologiskt : Olika föremål som kan associeras med specifika Long Count-datum har isotopdaterats . År 1959 koldaterade University of Pennsylvania prover från tio träöverliggare från Tikal . Dessa ristades med ett datum motsvarande 741 AD, med hjälp av GMT-korrelationen. Det genomsnittliga koldatumet var 746±34 år. Nyligen analyserades en av dessa, Lintel 3 från Temple I, igen med mer exakta metoder och visade sig stämma överens med GMT-korrelationen.

Om en föreslagen korrelation bara måste överensstämma med en av dessa bevis kan det finnas många andra möjligheter. Astronomer har föreslagit många korrelationer, till exempel: Lounsbury , Fuls, et al. , Böhm och Böhm och Stock.

Idag, 5 mars 2023 ( UTC ), i Long Count är 13.0.10.6.6 (med GMT-korrelation).



JDN-korrelationer till Mayas skapelsedatum (efter Thompson 1971, et al. och Aveni 1980)
namn Korrelation
Bowditch 394,483
Willson 438,906
Smiley 482 699
Makemson 489,138
Modifierad Spinden 489,383
Spinden 489,384
Teeple 492,622
Dinsmoor 497,879
−4CR 508,363
−2CR 546,323
Stock 556,408
Bra man 584,280
Martinez-Hernandez 584,281
GMT 584,283
Ändrad Thompson 1 584,284
Thompson (Lounsbury) 584,285
Pogo 588,626
+2CR 622,243
Böhm & Böhm 622,261
Kreichgauer 626,927
+4CR 660,203
Fuls, et al. 660 208
Hochleitner 674,265
Schultz 677,723
Escalona–Ramos 679,108
Vaillant 679,183
Weitzel 774 078
Lång räkning
(proleptisk före 1582) Gregorianskt datum GMT (584 283) korrelation
Julians dagnummer
0.0.0.0.0 Tors 1 april 8239 fvt -1 287 717
1.0.0.0.0 Sön 4 juli 7845 fvt -1 143 717
2.0.0.0.0 Onsdag 7 oktober 7451 f.Kr -999 717
3.0.0.0.0 Lör den 9 januari 7056 fvt -855 717
4.0.0.0.0 tis 14 april 6662 fvt -711 717
5.0.0.0.0 Fre den 17 juli 6268 fvt -567 717
6.0.0.0.0 mån den 20 oktober 5874 f.Kr -423 717
7.0.0.0.0 Tors den 22 januari 5479 fvt -279 717
8.0.0.0.0 Sön 26 april 5085 fvt -135 717
9.0.0.0.0 Onsdag 30 juli 4691 f.Kr 8,283
10.0.0.0.0 Lör den 1 november 4297 fvt 152,283
11.0.0.0.0 tis den 3 februari 3902 fvt 296,283
12.0.0.0.0 Fre den 8 maj 3508 fvt 440,283
13.0.0.0.0 mån 11 augusti 3114 f.Kr 584,283
1.0.0.0.0 Tors den 13 november 2720 f.Kr 728,283
2.0.0.0.0 Sön 16 februari 2325 fvt 872,283
3.0.0.0.0 Onsdagen den 21 maj 1931 f.Kr 1 016 283
4.0.0.0.0 Lör den 23 augusti 1537 fvt 1,160,283
5.0.0.0.0 tis den 26 november 1143 fvt 1,304,283
6.0.0.0.0 Fre den 28 februari 748 fvt 1,448,283
7.0.0.0.0 mån 3 juni 354 f.Kr 1,592,283
8.0.0.0.0 tor 5 sep 41 e.Kr 1,736,283
9.0.0.0.0 Sön 9 december 435 1,880,283
10.0.0.0.0 Ons 13 mars 830 2,024,283
11.0.0.0.0 Lör den 15 juni 1224 2,168,283
12.0.0.0.0 Tis 18 september 1618 2,312,283
13.0.0.0.0 Fre 21 december 2012 2,456,283
14.0.0.0.0 mån 26 mars 2407 2,600,283
15.0.0.0.0 Tors den 28 juni 2801 2,744,283
16.0.0.0.0 Sön 1 oktober 3195 2,888,283
17.0.0.0.0 Onsdag 3 januari 3590 3,032,283
18.0.0.0.0 Lör den 7 april 3984 3,176,283
19.0.0.0.0 Tis den 11 juli 4378 3,320,283
1.0.0.0.0.0 Fre den 13 oktober 4772 3,464,283

2012 och den långa greven

Huvudartikel: 2012 års fenomen

Enligt Popol Vuh , en bok som sammanställer detaljer om skapelseberättelser kända för K'iche' Maya från kolonialtidens högland, lever mänskligheten i den fjärde världen. Popol Vuh beskriver de tre första skapelserna som gudarna misslyckades med att skapa och skapandet av den framgångsrika fjärde världen där människor placerades. I Maya Long Count slutade den tidigare skapelsen i slutet av en 13:e bʼakʼtun.

Den tidigare skapelsen slutade på en långräkning av 12.19.19.17.19. Ytterligare en 12.19.19.17.19 inträffade den 20 december 2012 (gregoriansk kalender), följt av starten av den 14:e bʼakʼtun, 13.0.0.0.0, den 21 december 2012. Det finns bara två referenser till den nuvarande skapelsens 13:e bʼakʼ den fragmentariska Maya-korpusen: Tortuguero Monument 6, en del av en linjalinskription och den nyligen upptäckta La Corona Hieroglyphic Stairway 2, Block V.

Maya-inskriptioner hänvisar ibland till framtida förutspådda händelser eller minneshögtider som skulle inträffa på datum som ligger efter 2012 (det vill säga efter fullbordandet av den 13:e b'akʼtunen av den nuvarande eran). De flesta av dessa är i form av "distansdatum" där något Long Count-datum anges, tillsammans med ett Distansnummer som ska läggas till Long Count-datumet för att komma fram till detta framtida datum.

Till exempel, på den västra panelen vid Temple of Inscriptions i Palenque , projicerar en del av texten in i framtiden till 80-årsdagen av den berömda Palenque-härskaren K'inich Janaab ' Pakals trontillträde (CR) 80-årsdagen ( Pakals anslutning inträffade på ett kalenderrunda datum 5 Lamat 1 Mol, vid långräkning 9.9.2.4.8 motsvarande den 27 juli 615 CE i den proleptiska gregorianska kalendern ). Den gör detta genom att börja med Pakals födelsedatum 9.8.9.13.0 8 Ajaw 13 Pop (24 mars 603 CE gregoriansk ) och lägga till avståndsnumret 10.11.10.5.8.

Denna beräkning kommer fram till den 80:e kalenderrundan sedan hans tillträde, en dag som också har ett CR-datum på 5 Lamat 1 Mol , men som ligger över 4 000 år i framtiden från Pakals tid – dagen 21 oktober år 4772. Inskriften noterar [ citat behövs ] att denna dag skulle infalla åtta dagar efter fullbordandet av den 1:a piktunen (sedan skapandet eller nolldatumet för systemet med långa räkningar), där piktunen är den näst högsta ordningen över b'ak'tunen i den långa räkningen. Om slutdatumet för den piktunen – 13 oktober 4772 – skulle skrivas ut med långräkning, skulle det kunna representeras som 1.0.0.0.0.0. 80-årsdagen för CR, åtta dagar senare, skulle vara 1.0.0.0.0.8 5 Lamat 1 Mol.

Trots publiciteten som genererades av datumet 2012, uttalade Susan Milbrath, curator för latinamerikansk konst och arkeologi vid Florida Museum of Natural History , att "Vi har inga uppgifter eller vetskap om att [Maya] skulle tro att världen skulle gå under " år 2012. USA Today skriver " 'För den forntida Maya var det ett stort firande att ta sig till slutet av en hel cykel', säger Sandra Noble, verkställande direktör för Foundation for the Advancement of Mesoamerican Studies i Crystal River , Florida . Att framställa den 21 december 2012 som en undergångshändelse eller ett ögonblick av kosmiska förändringar, säger hon, är "ett komplett påhitt och en chans för många människor att tjäna pengar på." " Det kommer att bli en annan cykel", säger hon. E. Wyllys Andrews V, chef för Tulane University Middle American Research Institute (MARI). "Vi vet att Maya trodde att det fanns en före detta, och det betyder att de var bekväma med tanken på en annan efter detta."

Konvertera mellan långräkningen och västerländska kalendrar

Beräknar ett västerländskt kalenderdatum från en lång räkning

Det är viktigt att känna till skillnaden mellan den julianska och gregorianska kalendern när man beräknar ett västerländskt kalenderdatum från ett Long Count-datum.

Använd som ett exempel Long Count-datumet 9.10.11.17.0 (Long Count-datum som nämns på Palenque Palace Tablet), beräkna först antalet dagar som har gått sedan nolldatumet (11 augusti 3114 f.Kr.; GMT-korrelation, i den proleptiska gregorianska kalendern , 6 september −3113 Julian astronomical).

9 × 144 000 = 1 296 000
10 × 7 200 = 72 000
11 × 360 = 3,960
17 × 20 = 340
0 × 1 = 0
Totalt antal dagar = 1 372 300

Lägg sedan till GMT-korrelationen till det totala antalet dagar.

1 372 300 + 584 283 = 1 956 583

Detta nummer är en juliansk dag .

Så här konverterar du en juliansk dag till ett proleptiskt gregoriansk kalenderdatum :

Från detta tal, subtrahera det närmaste mindre julianska dagtalet (i tabellen nedan), i detta fall 1 940 206, vilket motsvarar år 600 e.Kr.

år JDN: år JDN:
1 1 721 060 1100 2,122,827
100 1,757,585 1200 2,159,351
200 1,794,109 1300 2,195,876
300 1,830,633 1400 2 232 400
400 1,867,157 1500 2,268,924
500 1,903,682 1600 2,305,448
600 1,940,206 1700 2,341,973
700 1,976,730 1800 2,378,497
800 2 013 254 1900 2,415,021
900 2 049 779 2000 2,451,545
1000 2,086,303
1 956 583 – 1 940 206 = 16 377

Dela sedan detta antal med 365 dagar (vagt år).

16 377 / 365 = 44,86849

Resten är 44,86849 år, vilket är 44 år och 317 dagar. Helårsdatumet är 644 e.Kr. Beräkna nu månads- och dagnummer, med hänsyn till skottdagar under de 44 åren. I den gregorianska kalendern är vart fjärde år ett skottår med undantag för århundraden som inte är jämnt delbara med 400 (t.ex. 100, 200, 300). När året är delbart med 400 (t.ex. 400, 800, etc.), lägg inte till en extra dag. Det beräknade året är 644 e.Kr. Antalet skottdagar, med tanke på att år 600 inte är ett skottår, är 10. Subtrahera det från 317 återstående dagar är 307; med andra ord, den 307:e dagen av år 644 e.Kr., vilket är 3 november. För att sammanfatta: Långräkningsdatumet 9.10.11.17.0 motsvarar 3 november 644 e.Kr. i den proleptiska gregorianska kalendern .

För att konvertera en juliansk dag till ett julianskt/gregorianskt astronomiskt datum ( proleptisk juliansk kalender före 46 f.Kr.):

Meeus -metoden för att konvertera den julianska dagen till ett julianskt/gregorianskt datum med astronomisk datering av negativa år:

I det här exemplet:


           
          

  
    

    
    
    
    






   

 
    

    

 
    

    

 ingång:  Julian dag  J  J  =  J  + 0,5  // 1 956 583,5  Z  = heltalsdel av  J  // 1 956 583  F  = bråkdel av  J  // 0,5  om  Z  < 2 299 161  då  // Julian?  A  =  Z  else  alpha  = floor((  Z  - 1 867 216,25) / 36 524,25)  // 15  A  =  Z  + 1 +  alpha  - floor(  alpha  / 4,0)  // 2 436 129  // Golvoperationen avrundar ett decimaltal nedåt till det näst lägsta heltal.  // Till exempel, floor(1.5) = 1 och floor(−1.5) = -2  end if  B  =  A  + 1524  // 1.958.107  C  = floor((  B  - 122.1) / 365.25)  // 5.360  D  = floor(365.25) ×  C  )  // 1 957 740  E  = golv((  B  -  D  ) / 30,6001)  // 11  dagar  =  B  -  D  - golv(30,6001 ×  E  ) +  F  // 31,5  om  E  < 14  sedan  månad  =  E  - 1  // 10  annan  månad  =  E  - 13  slut om  om  månad  > 2  sedan  år  =  C  - 4716  // 644  annat  år  =  C  - 4715  slut om  retur  (  år  ,  månad  ,  dag  )

I det här exemplet är det julianska datumet 12.00 den 31 oktober 644. Meeus -metoden är inte giltig för negativa årtal (astronomiska), så en annan metod som Peter Baums metod bör användas.

Beräknar ett fullständigt Long Count-datum

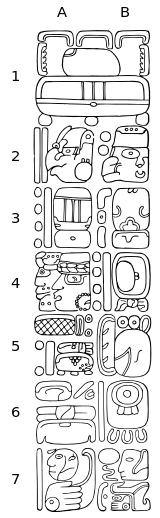
Chichen Itza Initial Series inskription. Detta datum (glyfer A2, B2, ..., A5) är 10.2.9.1.9 9 Muluk 7 Sak, motsvarande 28 juli 878 (GMT gregoriansk).

Ett fullständigt Long Count-datum inkluderar inte bara de fem siffrorna i Long Count, utan även Tzolkʼin-datumen med två tecken och Haabʼ-datumen med två tecken. Den femsiffriga långa räkningen kan därför bekräftas med de andra fyra tecknen ("kalendern runda datum").

Som exempel tar vi ett kalenderrunda datum 9.12.2.0.16 (Långt räknat) 5 Kibʼ (Tzolkʼin) 14 Yaxkʼin (Haabʼ). Man kan kontrollera om detta datum är korrekt genom följande beräkning.

Det är kanske lättare att ta reda på hur många dagar det är sedan 4 Ajaw 8 Kumkʼu och visa hur datumet 5 Kibʼ 14 Yaxkʼin härleds.

9 × 144 000 = 1296000
12 × 7200 = 86400
2 × 360 = 720
0 × 20 = 0
16 × 1 = 16
Totalt antal dagar = 1383136

Beräknar Tzolkʼin-datumdelen

Tzolkʼin-datumet räknas framåt från 4 Ajaw. För att beräkna den numeriska delen av Tzolkʼin-datumet, lägg till 4 till det totala antalet dagar som ges av datumet och dividera sedan det totala antalet dagar med 13.

(4 + 1 383 136) / 13 = 106 395 (och 5/13)

Detta betyder att 106 395 hela 13 dagars cykler har slutförts och den numeriska delen av Tzolkʼin-datumet är 5.

För att beräkna dagen, dividera det totala antalet dagar i den långa räkningen med 20 eftersom det finns tjugo dagnamn.

1 383 136 / 20 = 69 156 (och 16/20)

Detta betyder att 16 dagars namn måste räknas från Ajaw. Detta ger Kibʼ. Därför är Tzolkʼin-datumet 5 Kibʼ.

Beräknar Haab's datumdel

Haab's datum 8 Kumk'u är den nionde dagen i artonde månaden. Det är 17 dagar till början av nästa år.

Subtrahera 17 dagar från summan för att ta reda på hur många kompletta Haab' år som finns.

1 383 136 − 17 = 1 
 383 119 gånger 365
1 383 119 / 365 = 3 789 och (134/365)

Därför har 3 789 kompletta Haabʼ passerat och resten 134 är den 135:e dagen i den nya Haabʼ, eftersom en återstod av 0 skulle indikera den första dagen.

Ta reda på vilken månad dagen är i. Att dividera resten med 134 med 20 är sex hela månader och resten av 14, vilket indikerar den 15:e dagen. Så, datumet i Haab' ligger i den sjunde månaden, vilket är Yaxk'in. Den femtonde dagen av Yaxk'in är 14, så Haab's datum är 14 Yaxk'in.

Så datumet för långräkningsdatumet 9.12.2.0.16 5 Kibʼ 14 Yaxkʼin är bekräftat.

Piktuns och högre order

Det finns också fyra sällan använda högre ordningens perioder ovanför bʼakʼtun: piktun , kalabtun , kʼinchiltun och alautun . Alla dessa ord är uppfinningar av mayanister. Var och en består av 20 av de mindre enheterna.

Många inskriptioner anger datumet för den nuvarande skapelsen som ett stort antal 13:or före 13.0.0.0.0 4 Ahau 8 Kumkʼu. Till exempel ett senklassiskt monument från Coba , Stela 1. Skapandedatumet uttrycks som 13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.0.0.0.0, där enheterna är 1, de nitton platserna större än bʼakʼtun. Vissa författare tror att 13:orna var symboliska för en avslutning och inte representerar ett verkligt antal.

De flesta inskriptioner som använder dessa är i form av avståndsdatum och långa räkningar – de ger ett basdatum, ett avståndstal som adderas eller subtraheras och det resulterande långa räkningen.

Det första exemplet nedan är från Schele (1987). Den andra är från Stuart (2005 s. 60, 77)




Palenque Temple of the Cross, tablett, Schele (1987 s.) 12.19.13.4.0 8 Ajaw 18 Tzek i den tidigare eran 6.14.0 Distansnummer som länkar till "erans datum" 13.0.0.0.0 4 Ajaw 8 Kumkʼu




Palenque Temple XIX, South Panel G2-H6 Stuart (2005 s. 60, 77) 12.10.1.13.2 9 Ikʼ 5 Mol (säte för GI i den tidigare eran) 2.8.3.8.0 1.18.5.3.2 9 Ikʼ 15 Keh (återfödelse av GI, detta datum även i Temple of the Cross)




Tabletten med inskriptionerna innehåller denna inskription: 9.8.9.13.0 8 Ajaw 13 Pop 10.11.10.5.8 1.0.0.0.0.8

Dresden -codexen innehåller en annan metod för att skriva avståndsnummer. Dessa är ringnummer. Specifika datum inom Dresden-codexen ges ofta genom beräkningar som involverar ringnummer. Förstemann identifierade dessa, men Wilson (1924) klargjorde senare hur de fungerar. Ringnummer är intervall av dagar mellan Era Base-datum 4 Ajaw 8 Kumkʼu och ett tidigare Ring Base-datum, där platshållaren för antalet dagar i intervallet är inringad av en bild av ett bundet rött band. Till detta tidigare Ring Base-datum läggs ytterligare ett antal dagar framåt, som Thompson refererar till som en lång runda, vilket leder till ett slutdatum inom det långa antalet som anges som ett inträdesdatum för att användas i en specifik tabell i codexen.



Ringnummer (12) 12.12.17.3.1 13 Imix 9 Wo (7.2.14.19 före (13) 13.0.0.0.0) distansnummer (0) 10.13.13.3.2 Long Count 10.6.10.6.3 13 Akinbal 1 Kankʼ


Ringnummer (del av DN föregående era datum) 7.2.14.19 Lägg till Ringnummer till ringnummerdatumet för att nå 13.0.0.0.0

Thompson innehåller en tabell med typiska långa räkningar efter Satterwaite.

"Serpent Numbers" i Dresden codex s. 61–69 är en tabell över datum med basdatumet 1.18.1.8.0.16 i den tidigare eran (5 482 096 dagar).

Se även

Anteckningar

Bibliografi

externa länkar

Hämtad från " https://en.wikipedia.org/w/index.php?title=Mesoamerican_Long_Count_calendar&oldid=1140570051 "