Lista över vanliga polytoper och föreningar

Exempel på vanliga polytoper

Regelbundna (2D) polygoner
Konvex	Stjärna
{5}	{5/2}
Vanliga (3D) polyedrar
Konvex	Stjärna
{5,3}	{5/2,5}
Vanliga 4D polytoper
Konvex	Stjärna
{5,3,3}	{5/2,5,3}
Vanliga 2D-tesselationer
euklidisk	Hyperbolisk
{4,4}	{5,4}
Vanliga 3D-tesselationer
euklidisk	Hyperbolisk
{4,3,4}	{5,3,4}

Denna artikel listar de vanliga polytoperna och vanliga polytopföreningarna i euklidiska , sfäriska och hyperboliska utrymmen.

Schläfli -symbolen beskriver varje regelbunden tessellation av en n -sfär, euklidiska och hyperboliska rum. En Schläfli-symbol som beskriver en n -polytop beskriver ekvivalent en tessellation av en ( n − 1)-sfär. Dessutom uttrycks symmetrin hos en vanlig polytop eller tessellation som en Coxeter-grupp , som Coxeter uttryckte identiskt med Schläfli-symbolen, förutom att avgränsa med hakparenteser, en notation som kallas Coxeter-notation . En annan relaterad symbol är Coxeter-Dynkin-diagrammet som representerar en symmetrigrupp utan ringar, och den representerar vanlig polytop eller tessellation med en ring på den första noden. Till exempel kuben Schläfli-symbolen {4,3}, och med sin oktaedriska symmetri , [4,3] eller , representeras den av Coxeter-diagram .

De vanliga polytoperna är grupperade efter dimension och undergrupperade efter konvexa, icke-konvexa och oändliga former. Ickekonvexa former använder samma hörn som de konvexa formerna, men har skärande fasetter . Oändliga former bildar ett en-lägre dimensionellt euklidiskt rum.

Oändliga former kan utökas för att tessellate ett hyperboliskt utrymme . Hyperboliskt utrymme är som normalt utrymme i liten skala, men parallella linjer divergerar på avstånd. Detta tillåter vertexfigurer att ha negativa vinkeldefekter , som att göra en vertex med sju liksidiga trianglar och låta den ligga platt. Det kan inte göras i ett vanligt plan, men kan vara i rätt skala av ett hyperboliskt plan.

En mer allmän definition av vanliga polytoper som inte har enkla Schläfli-symboler inkluderar vanliga sneda polytoper och vanliga sneda apeirotoper med icke-plana fasetter eller vertexfigurer .

Översikt

Den här tabellen visar en sammanfattning av vanliga polytopräkningar per dimension.

Observera att de euklidiska och hyperboliska plattorna ges en dimension mer än vad som skulle förväntas. Detta beror på en analogi med ändliga polytoper: en konvex regelbunden n -polytop kan ses som en tessellation av ( n −1)-dimensionellt sfäriskt utrymme. Således är de tre regelbundna plattorna på det euklidiska planet (med trianglar, kvadrater och hexagoner) listade under dimension tre snarare än två.

Dämpa.	Ändlig			euklidisk	Hyperbolisk			Föreningar
					Kompakt		Paracompact
	Konvex	Stjärna	Skev	Konvex	Konvex	Stjärna	Konvex	Konvex	Stjärna
1	1	ingen	ingen	1	ingen	ingen	ingen	ingen	ingen
2	$\infty$	$\infty$	$\infty$	1	1	ingen	ingen	$\infty$	$\infty$
3	5	4	?	3	$\infty$	$\infty$	$\infty$	5	ingen
4	6	10	?	1	4	ingen	11	26	20
5	3	ingen	?	3	5	4	2	ingen	ingen
6	3	ingen	?	1	ingen	ingen	5	ingen	ingen
7	3	ingen	?	1	ingen	ingen	ingen	3	ingen
8	3	ingen	?	1	ingen	ingen	ingen	6	ingen
9+	3	ingen	?	1	ingen	ingen	ingen		ingen

Det finns inga euklidiska vanliga stjärntesselationer i hur många dimensioner som helst.

En dimension

Ett Coxeter-diagram representerar spegel-"plan" som noder, och sätter en ring runt en nod om en punkt inte är på planet. En dion { }, , är en punkt p och dess spegelbildspunkt p' , och linjesegmentet mellan dem.

En endimensionell polytop eller 1-polytop är ett slutet linjesegment , begränsat av dess två ändpunkter. En 1-polytop är regelbunden per definition och representeras av Schläfli-symbolen { }, eller ett Coxeter-diagram med en enda ringad nod, . Norman Johnson kallar den en dion och ger den Schläfli-symbolen { }.

Även om den är trivial som en polytop, framstår den som kanterna på polygoner och andra högre dimensionella polytoper. Det används i definitionen av enhetliga prismor som Schläfli-symbolen { }×{p} eller Coxeter-diagram som en kartesisk produkt av ett linjesegment och en vanlig polygon.

Två dimensioner (polygoner)

De tvådimensionella polytoperna kallas polygoner . Regelbundna polygoner är liksidiga och cykliska . En p-gonal regelbunden polygon representeras av Schläfli-symbolen {p}.

Vanligtvis anses endast konvexa polygoner vara regelbundna, men stjärnpolygoner , som pentagrammet , kan också anses vara regelbundna. De använder samma hörn som de konvexa formerna, men ansluter i en alternativ anslutning som passerar runt cirkeln mer än en gång för att slutföras.

Stjärnpolygoner bör kallas icke-konvexa snarare än konkava eftersom de skärande kanterna inte genererar nya hörn och alla hörn finns på en cirkelgräns.

Konvex

Schläfli-symbolen {p} representerar en vanlig p -gon .

namn	Triangel ( 2-simplex )	Fyrkantig ( 2-ortoplex ) ( 2-kub )	Pentagon ( 2-pentagonal polytop )	Sexhörning	Heptagon	Oktogon
Schläfli	{3}	{4}	{5}	{6}	{7}	{8}
Symmetri	D 3 , [3]	D 4 , [4]	D 5 , [5]	D 6 , [6]	D 7 , [7]	D 8 , [8]
Coxeter
bild
namn	Nonagon (Enneagon)	Decagon	Hendecagon	Dodecagon	Tridecagon	Tetradekagon
Schläfli	{9}	{10}	{11}	{12}	{13}	{14}
Symmetri	D 9 , [9]	D 10 , [10]	D 11 , [11]	D 12 , [12]	D 13 , [13]	D 14 , [14]
Dynkin
bild
namn	Pentadekagon	Hexadekagon	Heptadekagon	Octadecagon	Enneadekagon	Icosagon	...p-gon
Schläfli	{15}	{16}	{17}	{18}	{19}	{20}	{ p }
Symmetri	D 15 , [15]	D 16 , [16]	D 17 , [17]	D 18 , [18]	D 19 , [19]	D 20 , [20]	D p , [p]
Dynkin
bild

Sfärisk

Den reguljära digonen {2} kan anses vara en degenererad reguljär polygon. Det kan realiseras icke-degenererat i vissa icke-euklidiska utrymmen, såsom på ytan av en sfär eller torus . Till exempel kan digon realiseras icke-degenererat som en sfärisk lune . En monogon {1} kan också realiseras på sfären som en enda punkt med en stor cirkel genom den. En monogon är dock inte en giltig abstrakt polytop eftersom dess enda kant bara faller in på en vertex snarare än två.

namn	Monogon	Digon
Schläfli symbol	{1}	{2}
Symmetri	D 1 , [ ]	D 2 , [2]
Coxeter diagram	eller
Bild

Stjärnor

Det finns oändligt många vanliga stjärnpolytoper i två dimensioner, vars Schläfli-symboler består av rationella tal { n / m }. De kallas stjärnpolygoner och delar samma vertexarrangemang som de konvexa reguljära polygonerna.

I allmänhet, för alla naturliga tal n , finns det n-uddiga stjärnor regelbundna polygonala stjärnor med Schläfli-symboler { n / m } för alla m så att m < n /2 (strängt taget { n / m }={ n /( n − m )}) och m och n är coprime (som sådana kommer alla stellationer i en polygon med ett primtal av sidor att vara reguljära stjärnor). Fall där m och n inte är coprime kallas sammansatta polygoner .

namn	Pentagram	Heptagram		Oktagram	Enneagram		Dekagram	... n-gram
Schläfli	{5/2}	{7/2}	{7/3}	{8/3}	{9/2}	{9/4}	{10/3}	{ p/q }
Symmetri	D 5 , [5]	D 7 , [7]		D 8 , [8]	D 9 , [9],		D 10 , [10]	D p , [ p ]
Coxeter
bild

Vanliga stjärnpolygoner upp till 20 sidor

{11/2}	{11/3}	{11/4}	{11/5}	{12/5}	{13/2}	{13/3}	{13/4}	{13/5}	{13/6}
{14/3}	{14/5}	{15/2}	{15/4}	{15/7}	{16/3}	{16/5}	{16/7}
{17/2}	{17/3}	{17/4}	{17/5}	{17/6}	{17/7}	{17/8}	{18/5}	{18/7}
{19/2}	{19/3}	{19/4}	{19/5}	{19/6}	{19/7}	{19/8}	{19/9}	{20/3}	{20/7}	{20/9}

Stjärnpolygoner som bara kan existera som sfäriska plattsättningar, på samma sätt som monogonen och digonen, kan finnas (till exempel: {3/2}, {5/3}, {5/4}, {7/4}, {9/ 5}), men dessa verkar inte ha studerats i detalj.

Det finns också misslyckade stjärnpolygoner, såsom piangeln , som inte täcker ytan av en cirkel ändligt många gånger.

Skev polygoner

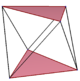
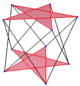
I 3-dimensionellt utrymme kallas en vanlig sned polygon en antiprismatisk polygon , med vertexarrangemanget av ett antiprisma och en delmängd av kanter, sicksackande mellan övre och nedre polygoner.

Exempel på vanliga sneda sicksackpolygoner

Sexhörning	Oktogon	Dekagoner
D 3d , [2 + ,6]	D 4d , [2 + ,8]	D 5d , [2 + ,10]
{3}#{ }	{4}#{ }	{5}#{ }	{5/2}#{ }	{5/3}#{ }

I 4-dimensioner kan en vanlig sned polygon ha hörn på en Clifford-torus och relaterad till en Clifford-förskjutning . Till skillnad från antiprismatiska snedställda polygoner kan snedställda polygoner vid dubbla rotationer innehålla ett udda antal sidor.

De kan ses i Petrie-polygonerna i de konvexa reguljära 4-polytoperna , ses som regelbundna plana polygoner i omkretsen av Coxeter-planprojektionen:

Pentagon	Oktogon	Dodecagon	Triakontagon
5-cell	16-celler	24-celler	600-celler

Tre dimensioner (polyhedra)

I tre dimensioner kallas polytoper polyedrar :

En vanlig polyeder med Schläfli-symbol {p,q}, Coxeter-diagram , har en regelbunden ansiktstyp {p} och regelbunden vertexfigur {q}.

En vertexfigur (av en polyeder) är en polygon, som ses genom att ansluta de hörn som är en kant bort från en given vertex. För vanliga polyedrar är denna vertexfigur alltid en regelbunden (och plan) polygon.

Existensen av en vanlig polyeder {p,q} begränsas av en olikhet, relaterad till vertexfigurens vinkeldefekt :

${\begin{aligned }&{\frac {1}{p}}+{\frac {1}{q}}>{\frac {1}{2}}:{\text{Polyhedron (finns i euklidiskt 3-rum)}} \\[6pt]&{\frac {1}{p}}+{\frac {1}{q}}={\frac {1}{2}}:{\text{Euklidiskt plan plattsättning}}\\ [6pt]&{\frac {1}{p}}+{\frac {1}{q}}<{\frac {1}{2}}:{\text{Hyperbolic plane tiling}}\end{aligned }}$

Genom att räkna upp permutationerna hittar vi fem konvexa former, fyra stjärnformer och tre plana plattsättningar, alla med polygoner {p} och {q} begränsade till: {3}, {4}, {5}, {5/2}, och {6}.

Bortom det euklidiska rymden finns det en oändlig uppsättning vanliga hyperboliska plattsättningar.

Konvex

De fem konvexa regelbundna polyedrarna kallas de platonska fasta kropparna . Hönssiffran anges med varje vertexräkning . Alla dessa polyedrar har en Euler-karaktäristik (χ) på 2.

namn	Schläfli {p,q}	Coxeter	Bild (fast)	Bild (sfär)	Ansikten {p}	Kanter	Vertices {q}	Symmetri	Dubbel
Tetraeder ( 3-simplex )	{3,3}				4 {3}	6	4 {3}	T d [3,3] (*332)	(själv)
Hexaederkub ( 3- kub )	{4,3}				6 {4}	12	8 {3}	O h [4,3] (*432)	Oktaeder
Oktaeder ( 3-ortoplex )	{3,4}				8 {3}	12	6 {4}	O h [4,3] (*432)	Kub
Dodekaeder	{5,3}				12 {5}	30	20 {3}	I h [5,3] (*532)	Icosahedron
Icosahedron	{3,5}				20 {3}	30	12 {5}	I h [5,3] (*532)	Dodekaeder

Sfärisk

I sfärisk geometri existerar regelbundna sfäriska polyedrar ( sfäriska plattor ) som annars skulle vara degenererade som polytoper . Dessa är hosoedrarna {2,n} och deras dubbla dihedrar {n,2}. Coxeter kallar dessa fall "olämpliga" tesselleringar.

De första fallen (n från 2 till 6) listas nedan.

Hosohedra

namn	Schläfli {2,p}	Coxeter diagram	Bild (sfär)	Ansikter {2} π/s	Kanter	Vertices {p}	Symmetri	Dubbel
Digonal hosohedron	{2,2}			2 {2} π/2	2	2 {2} π/2	D 2h [2,2] (*222)	Själv
Trigonal hosohedron	{2,3}			3 {2} π/3	3	2 {3}	D 3h [2,3] (*322)	Trigonal dihedron
Fyrkantig hosohedron	{2,4}			4 {2} π/4	4	2 {4}	D 4h [2,4] (*422)	Fyrkantig dihedron
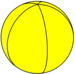
Pentagonal hosohedron	{2,5}			5 {2} π/5	5	2 {5}	D 5h [2,5] (*522)	Pentagonal dihedron
Hexagonal hosohedron	{2,6}			6 {2} π/6	6	2 {6}	D 6h [2,6] (*622)	Hexagonal dihedron

Dihedra

namn	Schläfli {s,2}	Coxeter diagram	Bild (sfär)	Ansikten {p}	Kanter	Vertices {2}	Symmetri	Dubbel
Digonal dihedron	{2,2}			2 {2} π/2	2	2 {2} π/2	D 2h [2,2] (*222)	Själv
Trigonal dihedron	{3,2}			2 {3}	3	3 {2} π/3	D 3h [3,2] (*322)	Trigonal hosohedron
Fyrkantig dihedron	{4,2}			2 {4}	4	4 {2} π/4	D 4h [4,2] (*422)	Fyrkantig hosohedron
Pentagonal dihedron	{5,2}			2 {5}	5	5 {2} π/5	D 5h [5,2] (*522)	Pentagonal hosohedron
Hexagonal dihedron	{6,2}			2 {6}	6	6 {2} π/6	D 6h [6,2] (*622)	Hexagonal hosohedron

Star-dihedra och hosohedra { p / q ,2} och {2, p / q } finns också för alla stjärnpolygoner { p / q }.

Stjärnor

De vanliga stjärnpolyedrarna kallas Kepler–Poinsot-polyedrarna och det finns fyra av dem, baserat på vertexarrangemangen för dodekaedern {5,3} och ikosaedern {3,5}:

Som sfäriska plattsättningar överlappar dessa stjärnaformer sfären flera gånger, kallad dess täthet och är 3 eller 7 för dessa former. Kakelbilderna visar en enda sfärisk polygonyta i gult.

namn	Bild (skelett)	Bild (fast)	Bild (sfär)	Stellationsdiagram _	Schläfli {p,q} och Coxeter	Ansikten {p}	Kanter	Vertices {q} verf.	χ	Densitet	Symmetri	Dubbel
Liten stjärnformad dodekaeder					{5/2,5}	12 {5/2}	30	12 {5}	−6	3	I h [5,3] (*532)	Stor dodekaeder
Stor dodekaeder					{5,5/2}	12 {5}	30	12 {5/2}	−6	3	I h [5,3] (*532)	Liten stjärnformad dodekaeder
Stor stjärnformad dodekaeder					{5/2,3}	12 {5/2}	30	20 {3}	2	7	I h [5,3] (*532)	Stor ikosaeder
Stor ikosaeder					{3,5/2}	20 {3}	30	12 {5/2}	2	7	I h [5,3] (*532)	Stor stjärnformad dodekaeder

Det finns oändligt många misslyckade stjärnpolyedrar. Dessa är också sfäriska plattsättningar med stjärnpolygoner i sina Schläfli-symboler, men de täcker inte en sfär ändligt många gånger. Några exempel är {5/2,4}, {5/2,9}, {7/2,3}, {5/2,5/2}, {7/2,7/3}, {4, 5/2} och {3,7/3}.

Skev polyedrar

Regelbundna sneda polyedrar är generaliseringar till uppsättningen av regelbundna polyhedrar som inkluderar möjligheten till icke-plana vertexfigurer .

För 4-dimensionella sneda polyedrar erbjöd Coxeter en modifierad Schläfli-symbol {l,m|n} för dessa figurer, där {l,m} antyder vertexfiguren , m l - goner runt en vertex och n -gonala hål. Deras vertexfigurer är sneda polygoner , sicksackande mellan två plan.

De vanliga sneda polyedrarna, representerade av {l,m|n}, följer denna ekvation:

2 sin(π/l) sin(π/m) = cos(π/n)

Fyra av dem kan ses i 4-dimensioner som en undergrupp av ytor av fyra vanliga 4-polytoper , som delar samma vertexarrangemang och kantarrangemang :

{4, 6 | 3}	{6, 4 | 3}	{4, 8 | 3}	{8, 4 | 3}

Fyra dimensioner

Vanliga 4-polytoper med Schläfli-symbolen $\{p,q,r\}$ har celler av typen $\{p,q\}$ , ytor av skriv $\{p\}$ , kantfigurer $\{r\}$ och vertexfigurer $\{q,r\}$ .

• En vertexfigur (av en 4-polytop) är en polyeder, sedd av arrangemanget av närliggande hörn runt en given vertex. För vanliga 4-polytoper är denna vertexfigur en vanlig polyeder.
• En kantfigur är en polygon, sedd genom arrangemanget av ytor runt en kant. För vanliga 4-polytoper kommer denna kantfigur alltid att vara en vanlig polygon.

Förekomsten av en vanlig 4-polytop $\{p,q,r\}$ begränsas av förekomsten av de reguljära polyedrarna ${\ displaystil \{p,q\},\{q,r\}}$ . Ett föreslaget namn för 4-polytoper är "polychoron".

Var och en kommer att existera i ett utrymme beroende på detta uttryck:

${\displaystyle \sin \left({\frac {\pi }{p}}\right)\sin \left({\frac { \pi }{r}}\right)-\cos \left({\frac {\pi }{q}}\right)} > {\displaystyle >0} : Hypersfärisk 3-$

$honeycomb$ eller 4-polytop

${ \displaystyle =0}$ : Euklidisk 3-mellanrums honeycomb

$<0$ : Hyperbolisk 3-space honeycomb

Dessa begränsningar tillåter 21 former: 6 är konvexa, 10 är icke-konvexa, en är en euklidisk bikaka med tre utrymmen och 4 är hyperboliska bikakor.

Eulerkarakteristiken $\chi$ för konvexa 4-polytoper är noll: $\displaystyle \chi =V+FEC=0}$ {

Konvex

De 6 konvexa vanliga 4-polytoperna visas i tabellen nedan. Alla dessa 4-polytoper har en Euler-karaktäristik (χ) på 0.

namn	Schläfli {p,q,r}	Coxeter	Celler {p,q}	Ansikten {p}	Kanter {r}	Vertices {q,r}	Dubbel {r,q,p}
5-celler ( 4-simplex )	{3,3,3}		5 {3,3}	10 {3}	10 {3}	5 {3,3}	(själv)
8-celler ( 4-kub ) (Tesseract)	{4,3,3}		8 {4,3}	24 {4}	32 {3}	16 {3,3}	16-celler
16-celler ( 4-ortoplex )	{3,3,4}		16 {3,3}	32 {3}	24 {4}	8 {3,4}	Tesseract
24-celler	{3,4,3}		24 {3,4}	96 {3}	96 {3}	24 {4,3}	(själv)
120-celler	{5,3,3}		120 {5,3}	720 {5}	1200 {3}	600 {3,3}	600-celler
600-celler	{3,3,5}		600 {3,3}	1200 {3}	720 {5}	120 {3,5}	120-celler

5-cell	8-cell	16-celler	24-celler	120-celler	600-celler
{3,3,3}	{4,3,3}	{3,3,4}	{3,4,3}	{5,3,3}	{3,3,5}
Trådram ( Petrie polygon ) snedställda ortografiska projektioner
Solida ortografiska projektioner
tetraedriskt hölje (cell/ vertexcentrerad)	kubiskt kuvert (cellcentrerat)	kubiskt kuvert (cellcentrerat)	kubiktaedriskt hölje (cellcentrerat)	trunkerat rombiskt triakontaederhölje ) (cellcentrerat	Pentakis icosidodecahedral kuvert (vertexcentrerad)
Wireframe Schlegel-diagram ( Perspektivprojektion )
(cellcentrerad)	(cellcentrerad)	(cellcentrerad)	(cellcentrerad)	(cellcentrerad)	(vertexcentrerad)
Wireframe stereografiska projektioner ( hypersfäriska )

Sfärisk

Di-4-toppar och hoso-4-toppar finns som vanliga tesseller av 3-sfären .

Vanliga di-4-toppar (2 fasetter) inkluderar: {3,3,2}, {3,4,2}, {4,3,2}, {5,3,2}, {3,5,2 }, {p,2,2} och deras hoso-4-top- dualer (2 hörn): {2,3,3}, {2,4,3}, {2,3,4}, {2, 3,5}, {2,5,3}, {2,2, p }. 4-polytoper av formen {2, p ,2} är samma som {2,2, p }. Det finns också fallen { p ,2, q } som har dihedriska celler och hosoedriska vertexfigurer.

Vanliga hoso-4-toppar som 3-sfäriska honungskakor

Schläfli {2, p , q }	Coxeter	Celler {2, p } π/ q	Ansikter {2} π/ p ,π/ q	Kanter	Vertices	Vertex figur { p , q }	Symmetri	Dubbel
{2,3,3}		4 {2,3} π/3	6 {2} π/3,π/3	4	2	{3,3}	[2,3,3]	{3,3,2}
{2,4,3}		6 {2,4} π/3	12 {2} π/4,π/3	8	2	{4,3}	[2,4,3]	{3,4,2}
{2,3,4}		8 {2,3} π/4	12 {2} π/3,π/4	6	2	{3,4}	[2,4,3]	{4,3,2}
{2,5,3}		12 {2,5} π/3	30 {2} π/5,π/3	20	2	{5,3}	[2,5,3]	{3,5,2}
{2,3,5}		20 {2,3} π/5	30 {2} π/3,π/5	12	2	{3,5}	[2,5,3]	{5,3,2}

Stjärnor

Det finns tio vanliga stjärna 4-polytoper , som kallas Schläfli–Hess 4-polytoper . Deras hörn är baserade på de konvexa 120-cellerna {5,3,3} och 600-cellerna {3,3,5} .

Ludwig Schläfli hittade fyra av dem och hoppade över de sista sex eftersom han inte skulle tillåta former som inte klarade Euler-karaktäristiken på celler eller vertexfigurer (för nollhåls tori: F+V−E=2). Edmund Hess (1843–1903) fullbordade hela listan på tio i sin tyska bok Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder ( 1883) [1] .

Det finns 4 unika kantarrangemang och 7 unika ansiktsarrangemang från dessa 10 vanliga stjärniga 4-polytoper, visade som ortogonala projektioner :

namn	Wireframe	Fast	Schläfli {p, q, r} Coxeter	Celler {p, q}	Ansikten {p}	Kanter {r}	Vertices {q, r}	Densitet	χ	Symmetrigrupp	Dubbla {r, q,p}
Icosahedral 120-cell (facetterad 600-cell)			{3,5,5/2}	120 {3,5}	1200 {3}	720 {5/2}	120 {5,5/2}	4	480	H4 [5,3,3 ]	Liten stjärnformad 120-cell
Liten stjärnformad 120-cell			{5/2,5,3}	120 {5/2,5}	720 {5/2}	1200 {3}	120 {5,3}	4	−480	H4 [5,3,3 ]	Icosahedral 120-cell
Bra 120-celler			{5,5/2,5}	120 {5,5/2}	720 {5}	720 {5}	120 {5/2,5}	6	0	H4 [5,3,3 ]	Självdubbel
Grand 120-cell			{5,3,5/2}	120 {5,3}	720 {5}	720 {5/2}	120 {3,5/2}	20	0	H4 [5,3,3 ]	Stora 120-celler
Stora 120-celler			{5/2,3,5}	120 {5/2,3}	720 {5/2}	720 {5}	120 {3,5}	20	0	H4 [5,3,3 ]	Grand 120-cell
Grand stellated 120-cell			{5/2,5,5/2}	120 {5/2,5}	720 {5/2}	720 {5/2}	120 {5,5/2}	66	0	H4 [5,3,3 ]	Självdubbel
Stora 120-celler			{5,5/2,3}	120 {5,5/2}	720 {5}	1200 {3}	120 {5/2,3}	76	−480	H4 [5,3,3 ]	Stor ikosaedrisk 120-cell
Stor ikosaedrisk 120-cell (bra fasetterad 600-cell)			{3,5/2,5}	120 {3,5/2}	1200 {3}	720 {5}	120 {5/2,5}	76	480	H4 [5,3,3 ]	Stora 120-celler
Grand 600-cell			{3,3,5/2}	600 {3,3}	1200 {3}	720 {5/2}	120 {3,5/2}	191	0	H4 [5,3,3 ]	Stora stellerade 120-celler
Stora stellerade 120-celler			{5/2,3,3}	120 {5/2,3}	720 {5/2}	1200 {3}	600 {3,3}	191	0	H4 [5,3,3 ]	Grand 600-cell

Det finns fyra misslyckade potentiella permutationer av vanliga stjärna 4-polytoper: {3,5/2,3}, {4,3,5/2}, {5/2,3,4}, {5/2,3,5 /2}. Deras celler och vertexfigurer finns, men de täcker inte en hypersfär med ett begränsat antal repetitioner.

Fem och fler dimensioner

I fem dimensioner kan en vanlig polytop namnges som $\{p,q,r,s\}$ där $\{p, q,r\}$ är 4-ansiktstypen, $\{p,q\}$ är celltypen, $\{p\}$ är ansiktstypen , och $\{s\}$ är ansiktsfiguren, $\{r,s\}$ är kantfiguren och ${\ displaystyle \{q,r,s\}}$ är vertexfiguren.

En vertexfigur (av en 5-polytop) är en 4-polytop, sedd av arrangemanget av närliggande hörn till varje vertex.

En kantfigur (av en 5-polytop) är en polyeder, sedd av arrangemanget av ytor runt varje kant.

En ansiktsfigur (av en 5-polytop) är en polygon som ses av arrangemanget av celler runt varje ansikte.

En vanlig 5-polytop $\{p,q,r,s\}$ finns bara om $\{p,q,r\ }$ och $\{q,r,s\}$ är vanliga 4-polytoper.

Utrymmet det passar i är baserat på uttrycket:

${\displaystyle {\frac {\cos ^{2}\left({\frac {\ pi }{q}}\right)}{\sin ^{2}\left({\frac {\pi}{p}}\right)}}+{\frac {\cos ^{2}\left( {\frac {\pi }{r}}\right)}{\sin ^{2}\left({\frac {\pi }{s}}\right)}}} < 1 {\displaystyle$

$}$ : Sfärisk 4-rymdstessellation eller 5-rymds polytop

$=1$ : Euklidisk 4-rymdstessellation

$>1$ : hyperbolisk 4-rymdstessellation

Uppräkning av dessa begränsningar ger 3 konvexa polytoper, noll icke-konvexa polytoper, 3 4-rymdstessellationer och 5 hyperboliska 4-space-tesselationer. Det finns inga icke-konvexa vanliga polytoper i fem dimensioner eller högre.

Konvex

I dimensionerna 5 och högre finns det bara tre typer av konvexa vanliga polytoper.

namn	Schläfli Symbol {p 1 ,...,p n −1 }	Coxeter	k -ansikten	Fasetttyp _	Vertex figur	Dubbel
n -enkelt	{3 n −1 }	...	${{n+1} \choose {k+1}}$	{3 n −2 }	{3 n −2 }	Självdubbel
n -kub	{4,3 n −2 }	...	$2^{nk}{n \choose k}$	{4,3 n −3 }	{3 n −2 }	n -ortoplex
n -ortoplex	{3 n −2 ,4}	...	$2^{k+1}{n \choose {k+1}}$	{3 n −2 }	{3 n −3 ,4}	n -kub

Det finns också felaktiga fall där vissa siffror i Schläfli-symbolen är 2. Till exempel är {p,q,r,...2} en felaktig regelbunden sfärisk polytop när {p,q,r...} är en regelbunden polytop. sfärisk polytop, och {2,...p,q,r} är en felaktig vanlig sfärisk polytop närhelst {...p,q,r} är en vanlig sfärisk polytop. Sådana polytoper kan också användas som fasetter, vilket ger former såsom {p,q,...2...y,z}.

5 dimensioner

namn	Schläfli Symbol {p,q,r,s} Coxeter	Fasetter {p,q,r}	Celler {p,q}	Ansikten {p}	Kanter	Vertices	Ansiktsfigur {s }	Kantfigur {r,s }	Hönsfigur {q,r , s}
5-simplex	{3,3,3,3}	6 {3,3,3}	15 {3,3}	20 {3}	15	6	{3}	{3,3}	{3,3,3}
5-kub	{4,3,3,3}	10 {4,3,3}	40 {4,3}	80 {4}	80	32	{3}	{3,3}	{3,3,3}
5-ortoplex	{3,3,3,4}	32 {3,3,3}	80 {3,3}	80 {3}	40	10	{4}	{3,4}	{3,3,4}

5-simplex

5-kub

5-ortoplex

6 dimensioner

namn	Schläfli	Vertices	Kanter	Ansikten	Celler	4-ansikten	5-ansikten	χ
6-simplex	{3,3,3,3,3}	7	21	35	35	21	7	0
6-kub	{4,3,3,3,3}	64	192	240	160	60	12	0
6-ortoplex	{3,3,3,3,4}	12	60	160	240	192	64	0

6-simplex

6-kub

6-ortoplex

7 dimensioner

namn	Schläfli	Vertices	Kanter	Ansikten	Celler	4-ansikten	5-ansikten	6-ansikten	χ
7-simplex	{3,3,3,3,3,3}	8	28	56	70	56	28	8	2
7-kub	{4,3,3,3,3,3}	128	448	672	560	280	84	14	2
7-ortoplex	{3,3,3,3,3,4}	14	84	280	560	672	448	128	2

7-simplex

7-kub

7-ortoplex

8 dimensioner

namn	Schläfli	Vertices	Kanter	Ansikten	Celler	4-ansikten	5-ansikten	6-ansikten	7-ansikten	χ
8-simplex	{3,3,3,3,3,3,3}	9	36	84	126	126	84	36	9	0
8-kub	{4,3,3,3,3,3,3}	256	1024	1792	1792	1120	448	112	16	0
8-ortoplex	{3,3,3,3,3,3,4}	16	112	448	1120	1792	1792	1024	256	0

8-simplex

8-kub

8-ortoplex

9 dimensioner

namn	Schläfli	Vertices	Kanter	Ansikten	Celler	4-ansikten	5-ansikten	6-ansikten	7-ansikten	8-ansikten	χ
9-simplex	{3 8 }	10	45	120	210	252	210	120	45	10	2
9-kub	{4,3 7 }	512	2304	4608	5376	4032	2016	672	144	18	2
9-ortoplex	{3 7 ,4}	18	144	672	2016	4032	5376	4608	2304	512	2

9-simplex

9-kub

9-ortoplex

10 dimensioner

namn	Schläfli	Vertices	Kanter	Ansikten	Celler	4-ansikten	5-ansikten	6-ansikten	7-ansikten	8-ansikten	9-ansikten	χ
10-simplex	{3 9 }	11	55	165	330	462	462	330	165	55	11	0
10-kub	{4,3 8 }	1024	5120	11520	15360	13440	8064	3360	960	180	20	0
10-ortoplex	{3 8 ,4}	20	180	960	3360	8064	13440	15360	11520	5120	1024	0

10-simplex

10-kub

10-ortoplex

...

Icke-konvex

Det finns inga icke-konvexa reguljära polytoper i fem dimensioner eller högre, exklusive hosotoper bildade av icke-konvexa reguljära polytoper med lägre dimensioner.

Vanliga projektiva polytoper

En projektiv reguljär ( n +1)-polytop existerar när en ursprunglig regelbunden n -sfärisk tessellation, {p,q,...}, är centralt symmetrisk . En sådan polytop heter hemi-{p,q,...} och innehåller hälften så många element. Coxeter ger en symbol {p,q,...}/2, medan McMullen skriver {p,q,...} _h/2 med h som coxeternummer .

Jämnsidiga regelbundna polygoner har hemi- 2n -gon projektiva polygoner, {2p}/2.

Det finns 4 regelbundna projektiva polyedrar relaterade till 4 av 5 platoniska fasta kroppar .

Hemi-kuben och hemi-oktaedern generaliserar som hemi- n -kuber och hemi- n - ortoplexer i alla dimensioner.

Regelbundna projektiva polyedrar

3-dimensionella vanliga hemi-polytoper

namn	Coxeter McMullen	Bild	Ansikten	Kanter	Vertices	χ
Hemi-kub	{4,3}/2 {4,3} 3		3	6	4	1
Hemi-oktaeder	{3,4}/2 {3,4} 3		4	6	3	1
Hemi-dodekaeder	{5,3}/2 {5,3} 5		6	15	10	1
Hemi-icosahedron	{3,5}/2 {3,5} 5		10	15	6	1

Vanliga projektiva 4-polytoper

I 4-dimensioner genererar 5 av 6 konvexa vanliga 4-polytoper projektiva 4-polytoper. De 3 specialfallen är hemi-24-cell, hemi-600-cell och hemi-120-cell.

4-dimensionella vanliga hemi-polytoper

namn	Coxeter symbol	McMullen symbol	Celler	Ansikten	Kanter	Vertices	χ
Hemi- tesseract	{4,3,3}/2	{4,3,3} 4	4	12	16	8	0
Hemi- 16-cell	{3,3,4}/2	{3,3,4} 4	8	16	12	4	0
Hemi- 24-cell	{3,4,3}/2	{3,4,3} 6	12	48	48	12	0
Hemi- 120-cell	{5,3,3}/2	{5,3,3} 15	60	360	600	300	0
Hemi- 600-cell	{3,3,5}/2	{3,3,5} 15	300	600	360	60	0

Vanliga projektiva 5-polytoper

Det finns bara 2 konvexa reguljära projektiva hemipolytoper i dimensionerna 5 eller högre: de är hemiversionerna av den vanliga hyperkuben och ortoplexen. De är tabellerade nedan i dimension 5, till exempel:

namn	Schläfli	4-ansikten	Celler	Ansikten	Kanter	Vertices	χ
hemi- penterakt	{4,3,3,3}/2	5	20	40	40	16	1
halv- pentacross	{3,3,3,4}/2	16	40	40	20	5	1

Apeirotoper

En apeirotop eller oändlig polytop är en polytop som har oändligt många facetter . En n -apeirotop är en oändlig n -polytop: en 2-apeirotop eller apeirogon är en oändlig polygon, en 3-apeirotop eller apeirohedron är en oändlig polyeder, etc.

Det finns två huvudsakliga geometriska klasser av apeirotop:

• Vanliga honungskakor i n dimensioner, som helt fyller ett n -dimensionellt utrymme.
• Regelbundna skeva apeirotoper , bestående av ett n -dimensionellt grenrör i ett högre utrymme.

En dimension (apeirogoner)

Den raka apeirogonen är en regelbunden tessellation av linjen, som delar upp den i oändligt många lika segment. Den har oändligt många hörn och kanter. Dess Schläfli-symbol är {∞}, och Coxeter-diagrammet .

... ...

Den existerar eftersom gränsen för p -gonen eftersom p tenderar till oändlighet, enligt följande:

namn	Monogon	Digon	Triangel	Fyrkant	Pentagon	Sexhörning	Heptagon	p-gon	Apeirogon
Schläfli	{1}	{2}	{3}	{4}	{5}	{6}	{7}	{ p }	{∞}
Symmetri	D 1 , [ ]	D 2 , [2]	D 3 , [3]	D 4 , [4]	D 5 , [5]	D 6 , [6]	D 7 , [7]	[p]
Coxeter	eller
Bild

Apeirogoner i det hyperboliska planet , mest notably den regelbundna apeirogonen , {∞}, kan ha en krökning precis som ändliga polygoner på det euklidiska planet, med hörn omskrivna av horocykler eller hypercykler snarare än cirklar .

Regelbundna apeirogoner som är skalade för att konvergera i oändligheten har symbolen {∞} och finns på horocykler, medan de mer generellt kan existera på hypercykler.

{∞}	{πi/λ}
Apeirogon på horocykel	Apeirogon på hypercykel

Ovan finns två regelbundna hyperboliska apeirogoner i Poincaré-skivmodellen , den högra visar vinkelräta reflektionslinjer av divergerande fundamentala domäner , åtskilda av längden λ.

Skeva apeirogoner

En sned apeirogon i två dimensioner bildar en sicksacklinje i planet. Om sicksacken är jämn och symmetrisk, är apeirogonen regelbunden.

Skew apeirogons kan konstrueras i valfritt antal dimensioner. I tre dimensioner spårar en vanlig sned apeirogon ut en spiralformad spiral och kan vara antingen vänster- eller högerhänt.

2-dimensioner	3-dimensioner
Sicksack apeirogon	Helix apeirogon

Två dimensioner (apeirohedra)

Euklidiska plattsättningar

Det finns tre vanliga tesselleringar av planet. Alla tre har en Euler-karaktäristik (χ) på 0.

namn	Fyrkantig kakel (quadrille)	Triangulär plattsättning (deltille)	Hexagonal plattsättning (hextile)
Symmetri	p4m, [4,4], (*442)	p6m, [6,3], (*632)
Schläfli {p,q}	{4,4}	{3,6}	{6,3}
Coxeter diagram
Bild

Det finns två felaktiga regelbundna plattor: {∞,2}, en apeirogonal dihedron , gjord av två apeirogoner , som var och en fyller halva planet; och för det andra dess dubbla, {2,∞}, en apeirogonal hosohedron , sedd som en oändlig uppsättning parallella linjer.

{∞,2} ,

{2,∞} ,

Euklidiska stjärntegelplattor

Det finns inga vanliga plana plattsättningar av stjärnpolygoner . Det finns många uppräkningar som passar i planet (1/ p + 1/ q = 1/2), som {8/3,8}, {10/3,5}, {5/2,10}, {12 /5,12}, etc., men ingen upprepas med jämna mellanrum.

Hyperboliska plattor

Tessellations av hyperboliskt 2-mellanrum är hyperboliska plattsättningar . Det finns oändligt många vanliga plattsättningar i H ² . Som nämnts ovan, varje positivt heltalspar { p , q } så att 1/ p + 1/ q < 1/2 ger en hyperbolisk sida. Faktum är att för den allmänna Schwarz-triangeln ( p , q , r ) gäller samma sak för 1/ p + 1/ q + 1/ r < 1.

Det finns ett antal olika sätt att visa det hyperboliska planet, inklusive Poincaré-skivmodellen som mappar planet till en cirkel, som visas nedan. Det bör noteras att alla polygonytorna i plattorna nedan är lika stora och bara verkar bli mindre nära kanterna på grund av den applicerade projiceringen, mycket lik effekten av en kameras fisheye- lins .

Det finns oändligt många platta regelbundna 3-apeirotoper (apeirohedra) som regelbundna plattsättningar av det hyperboliska planet, av formen {p,q}, med p+q<pq/2. (tidigare listad ovan som tesseller)

• {3,7}, {3,8}, {3,9} ... {3,∞}
• {4,5}, {4,6}, {4,7} ... {4,∞}
• {5,4}, {5,5}, {5,6} ... {5,∞}
• {6,4}, {6,5}, {6,6} ... {6,∞}
• {7,3}, {7,4}, {7,5} ... {7,∞}
• {8,3}, {8,4}, {8,5} ... {8,∞}
• {9,3}, {9,4}, {9,5} ... {9,∞}
• ...
• {∞,3}, {∞,4}, {∞,5} ... {∞,∞}

Ett urval:

Vanligt hyperboliskt kakelbord
Sfäriska (olämpliga / platoniska) / euklidiska / hyperboliska (Poincaré-skiva: kompakt / parakompakt / icke-kompakt ) tessellationer med deras Schläfli-symbol
p \ q	2	3	4	5	6	7	8	...	∞	...	iπ/λ
2	{2 , 2}	{2,3}	{2,4}	{2,5}	{2,6}	{2,7}	{2,8}		{2,∞}		{2,iπ/λ}
3	{3,2}	( tetraeder ) {3,3}	( oktaeder ) {3,4}	( ikosaeder ) {3,5}	( deltille ) {3,6}	{3,7}	{3,8}		{3,∞}		{3,iπ/λ}
4	{4,2}	( kub ) {4,3}	( quadrille ) {4,4}	{4,5}	{4,6}	{4,7}	{4,8}		{4,∞}		{4,iπ/λ}
5	{5,2}	( dodekaeder ) {5,3}	{5,4}	{5,5}	{5,6}	{5,7}	{5,8}		{5,∞}		{5,iπ/λ}
6	{6,2}	( hextille ) {6,3}	{6,4}	{6,5}	{6,6}	{6,7}	{6,8}		{6,∞}		{6,iπ/λ}
7	{7,2}	{7,3}	{7,4}	{7,5}	{7,6}	{7,7}	{7,8}		{7,∞}		{7,iπ/λ}
8	{8,2}	{8,3}	{8,4}	{8,5}	{8,6}	{8,7}	{8,8}		{8,∞}		{8,iπ/λ}
...
∞	{∞,2}	{∞,3}	{∞,4}	{∞,5}	{∞,6}	{∞,7}	{∞,8}	{∞,∞}	{∞,iπ/λ}
...
iπ/λ	{iπ/λ,2}	{iπ/λ,3}	{iπ/λ,4}	{iπ/λ,5}	{iπ/λ,6}	{iπ/λ,7}	{iπ/λ,8}	{iπ/λ,∞}	{iπ/λ, iπ/λ}

Plattorna {p, ∞} har idealiska hörn, på kanten av Poincaré-skivmodellen. Deras dualer {∞, p} har idealiska apeirogonala ansikten, vilket betyder att de är inskrivna i horocykler . Man skulle kunna gå längre (som görs i tabellen ovan) och hitta plattsättningar med ultraideala hörn, utanför Poincaré-skivan, som är dubbla till plattor inskrivna i hypercykler ; i det som symboliseras {p, iπ/λ} ovan, passar fortfarande oändligt många brickor runt varje ultraideal vertex. (Parallella linjer i utökat hyperboliskt utrymme möts vid en ideal punkt; ultraparallella linjer möts vid en ultra-ideal punkt.)

Hyperboliska stjärnplattor

Det finns 2 oändliga former av hyperboliska plattsättningar vars ytor eller vertexfigurer är stjärnpolygoner: { m /2, m } och deras dualer { m , m /2} med m = 7, 9, 11, .... Den { m /2, m } plattsättningar är stellationer av { m , 3} plattsättningar medan { m , m /2} dubbla plattsättningar är fasetteringar av {3, m } plattsättningar och förhöjningar av { m , 3} plattsättningar.

Mönstren { m /2, m } och { m , m /2} fortsätter för udda m < 7 som polyedrar : när m = 5 får vi den lilla stellerade dodekaedern och den stora dodekaedern , och när m = 3 degenererar fallet till en tetraeder . De andra två Kepler-Poinsot-polyedrarna (den stora stjärnbildade dodekaedern och den stora ikosaedern ) har inga vanliga analoger med hyperboliska plattor. Om m är jämnt, beroende på hur vi väljer att definiera { m /2}, kan vi antingen erhålla degenererade dubbelbeläggningar av andra plattsättningar eller sammansatta plattsättningar.

namn	Schläfli	Coxeter diagram	Bild	Ansiktstyp {p}	Hönsfigur {q}	Densitet	Symmetri	Dubbel
Order-7 heptagrammisk plattsättning	{7/2,7}			{7/2}	{7}	3	*732 [7,3]	Heptagonal plattsättning av heptagrammisk ordning
Heptagonal plattsättning av heptagrammisk ordning	{7,7/2}			{7}	{7/2}	3	*732 [7,3]	Order-7 heptagrammisk plattsättning
Order-9 enneagrammisk plattsättning	{9/2,9}			{9/2}	{9}	3	*932 [9,3]	Enneagrammisk ordning enneagonal plattsättning
Enneagrammisk ordning enneagonal plattsättning	{9,9/2}			{9}	{9/2}	3	*932 [9,3]	Order-9 enneagrammisk plattsättning
Order-11 hendecagrammic plattsättning	{11/2,11}			{11/2}	{11}	3	*11.3.2 [11,3]	Hendecagrammic-order hendecagonal plattsättning
Hendecagrammic-order hendecagonal plattsättning	{11,11/2}			{11}	{11/2}	3	*11.3.2 [11,3]	Order-11 hendecagrammic plattsättning
Ordnings- p p -grammisk plattsättning	{ p /2, p }			{ p /2}	{ p }	3	* s 32 [s, 3]	p -grammisk ordning p -gonal plattsättning
p -grammisk ordning p -gonal plattsättning	{ p , p /2}			{ p }	{ p /2}	3	* s 32 [s, 3]	Ordnings- p p -grammisk plattsättning

Skev apeirohedra i euklidiskt 3-utrymme

Det finns tre vanliga skeva apeirohedra i euklidiska 3-rum, med regelbundna sneda polygonvertexfigurer . De delar samma vertexarrangemang och kantarrangemang av 3 konvexa enhetliga bikakor .

• 6 rutor runt varje hörn: {4,6|4}
• 4 hexagoner runt varje vertex: {6,4|4}
• 6 hexagoner runt varje vertex: {6,6|3}

12 "rena" apeirohedra i euklidiskt 3-rum baserat på strukturen av den kubiska bikakan , {4,3,4}. En π petrie-dubbeloperator ersätter ytor med petriepolygoner ; δ är en dubbeloperator som vänder om hörn och ytor; φ _k är en k: te fasetteringsoperator; η är en halveringsoperator och σ skevningshalveringsoperator.

Vanliga sneda polyedrar
{4,6|4}	{6,4|4}	{6,6|3}

Det finns trettio regelbundna apeiroedrar i det euklidiska 3-rummet. Dessa inkluderar de som listas ovan, såväl som 8 andra "rena" apeirohedrar, alla relaterade till den kubiska bikakan, {4,3,4}, med andra som har sneda polygonytor: {6,6} ₄ , {4,6} ₄ , {6,4} ₆ , {∞,3} ^a , {∞,3} ^b , {∞,4} ^.*3 , {∞,4} _6,4 , {∞,6} _4,4 , och {∞,6} _6,3 .

Skev apeirohedra i hyperboliskt 3-mellanslag

Det finns 31 vanliga skeva apeiroedrar i hyperboliska 3-mellanrum:

• 14 är kompakta: {8,10|3}, {10,8|3}, {10,4|3}, {4,10|3}, {6,4|5}, {4,6|5 }, {10,6|3}, {6,10|3}, {8,8|3}, {6,6|4}, {10,10|3},{6,6|5}, {8,6|3} och {6,8|3}.
• 17 är parakompakta: {12,10|3}, {10,12|3}, {12,4|3}, {4,12|3}, {6,4|6}, {4,6|6 }, {8,4|4}, {4,8|4}, {12,6|3}, {6,12|3}, {12,12|3}, {6,6|6}, {8,6|4}, {6,8|4}, {12,8|3}, {8,12|3} och {8,8|4}.

Tre dimensioner (4-apeirotoper)

Tessellations av euklidiskt 3-rum

Kantram av kubisk honungskaka, {4,3,4}

Det finns bara en icke-degenererad regelbunden tessellation av 3-mellanrum ( honeycombs ), {4, 3, 4}:

namn	Schläfli {p,q,r}	Coxeter	Celltyp {p,q }	Ansiktstyp { p}	Kantfigur { r }	Hönsfigur } {q,r	χ	Dubbel
Kubisk honungskaka	{4,3,4}		{4,3}	{4}	{4}	{3,4}	0	Självdubbel

Felaktiga tesselleringar av euklidiskt 3-rum

Vanlig {2,4,4} honeycomb, sett projicerad in i en sfär.

Det finns sex felaktiga vanliga tesseller, par baserade på de tre vanliga euklidiska plattorna. Deras celler och vertexfigurer är alla vanliga hosohedra {2,n}, dihedra , {n,2} och euklidiska plattsättningar. Dessa felaktiga regelbundna plattsättningar är konstruktionsmässigt relaterade till prismatiska enhetliga bikakor genom trunkeringsoperationer. De är högredimensionella analoger av ordningen-2 apeirogonal plattsättning och apeirogonal hosohedron .

Schläfli {p,q,r}	Coxeter diagram	Celltyp {p,q }	Ansiktstyp { p}	Kantfigur { r }	Hönsfigur } {q,r
{2,4,4}		{2,4}	{2}	{4}	{4,4}
{2,3,6}		{2,3}	{2}	{6}	{3,6}
{2,6,3}		{2,6}	{2}	{3}	{6,3}
{4,4,2}		{4,4}	{4}	{2}	{4,2}
{3,6,2}		{3,6}	{3}	{2}	{6,2}
{6,3,2}		{6,3}	{6}	{2}	{3,2}

Tessellations av hyperboliskt 3-rum

Det finns tio platta vanliga bikakor med hyperboliskt 3-mellanslag: (tidigare listad ovan som tesseller)

• 4 är kompakta: {3,5,3}, {4,3,5}, {5,3,4} och {5,3,5}
• medan 6 är parakompakta: {3,3,6}, {6,3,3}, {3,4,4}, {4,4,3}, {3,6,3}, {4,3, 6}, {6,3,4}, {4,4,4}, {5,3,6}, {6,3,5} och {6,3,6}.

4 kompakta vanliga honungskakor {5,3,4} {5,3,5} {4,3,5} {3,5,3}

4 av 11 paracompact vanliga honeycombs {3,4,4} {3,6,3} {4,4,3} {4,4,4}

Tessellations av hyperboliska 3-mellanrum kan kallas hyperboliska honeycombs . Det finns 15 hyperboliska honeycombs i H ³ , 4 compact och 11 paracompact.

4 kompakta vanliga honungskakor

namn	Schläfli -symbol {p,q,r}	Coxeter	Celltyp {p,q }	Ansiktstyp { p}	Kantfigur { r }	Hönsfigur } {q,r	χ	Dubbel
Ikosaedrisk honungskaka	{3,5,3}		{3,5}	{3}	{3}	{5,3}	0	Självdubbel
Beställ-5 kubik honeycomb	{4,3,5}		{4,3}	{4}	{5}	{3,5}	0	{5,3,4}
Order-4 dodekaedrisk honungskaka	{5,3,4}		{5,3}	{5}	{4}	{3,4}	0	{4,3,5}
Order-5 dodekaedrisk honungskaka	{5,3,5}		{5,3}	{5}	{5}	{3,5}	0	Självdubbel

Det finns också 11 parakompakta H ³ -bikakor (de med oändliga (euklidiska) celler och/eller vertexfigurer): {3,3,6}, {6,3,3}, {3,4,4}, {4, 4,3}, {3,6,3}, {4,3,6}, {6,3,4}, {4,4,4}, {5,3,6}, {6,3, 5} och {6,3,6}.

11 paracompact vanliga honungskakor

namn	Schläfli -symbol {p,q,r}	Coxeter	Celltyp {p,q }	Ansiktstyp { p}	Kantfigur { r }	Hönsfigur } {q,r	χ	Dubbel
Order-6 tetraedrisk honungskaka	{3,3,6}		{3,3}	{3}	{6}	{3,6}	0	{6,3,3}
Sexkantigt kakelkaka	{6,3,3}		{6,3}	{6}	{3}	{3,3}	0	{3,3,6}
Order-4 oktaedrisk honungskaka	{3,4,4}		{3,4}	{3}	{4}	{4,4}	0	{4,4,3}
Fyrkantig kakelkaka	{4,4,3}		{4,4}	{4}	{3}	{4,3}	0	{3,3,4}
Triangulär kakelkaka	{3,6,3}		{3,6}	{3}	{3}	{6,3}	0	Självdubbel
Beställ-6 kubisk honungskaka	{4,3,6}		{4,3}	{4}	{4}	{3,6}	0	{6,3,4}
Order-4 hexagonal kakelkaka	{6,3,4}		{6,3}	{6}	{4}	{3,4}	0	{4,3,6}
Order-4 fyrkantiga kakel bikaka	{4,4,4}		{4,4}	{4}	{4}	{4,4}	0	Självdubbel
Order-6 dodekaedrisk honungskaka	{5,3,6}		{5,3}	{5}	{5}	{3,6}	0	{6,3,5}
Order-5 hexagonal kakel honeycomb	{6,3,5}		{6,3}	{6}	{5}	{3,5}	0	{5,3,6}
Order-6 hexagonal kakelkaka	{6,3,6}		{6,3}	{6}	{6}	{3,6}	0	Självdubbel

Icke-kompakta lösningar existerar som Lorentzian Coxeter-grupper och kan visualiseras med öppna domäner i hyperboliskt utrymme (den grundläggande tetraedern har ultraideala hörn). Alla bikakor med hyperboliska celler eller vertexfigurer och inte har 2 i sin Schläfli-symbol är icke-kompakta.

Sfäriska (olämpliga / platoniska) / euklidiska / hyperboliska ( kompakta / parakompakta / icke-kompakta) bikakor {p,3,r}

{ p ,3} \ r	2	3	4	5	6	7	8	... ∞
{2,3}	{2,3,2}	{2,3,3}	{2,3,4}	{2,3,5}	{2,3,6}	{2,3,7}	{2,3,8}	{2,3,∞}
{3,3}	{3,3,2}	{3,3,3}	{3,3,4}	{3,3,5}	{3,3,6}	{3,3,7}	{3,3,8}	{3,3,∞}
{4,3}	{4,3,2}	{4,3,3}	{4,3,4}	{4,3,5}	{4,3,6}	{4,3,7}	{4,3,8}	{4,3,∞}
{5,3}	{5,3,2}	{5,3,3}	{5,3,4}	{5,3,5}	{5,3,6}	{5,3,7}	{5,3,8}	{5,3,∞}
{6,3}	{6,3,2}	{6,3,3}	{6,3,4}	{6,3,5}	{6,3,6}	{6,3,7}	{6,3,8}	{6,3,∞}
{7,3}	{7,3,2}	{7,3,3}	{7,3,4}	{7,3,5}	{7,3,6}	{7,3,7}	{7,3,8}	{7,3,∞}
{8,3}	{8,3,2}	{8,3,3}	{8,3,4}	{8,3,5}	{8,3,6}	{8,3,7}	{8,3,8}	{8,3,∞}
... {∞,3}	{∞,3,2}	{∞,3,3}	{∞,3,4}	{∞,3,5}	{∞,3,6}	{∞,3,7}	{∞,3,8}	{∞,3,∞}

{s,4,r} { p ,4} \ r 2 3 4 5 6 ∞ {2,4} {2,4,2} {2,4,3} {2,4,4} {2,4,5} {2,4,6} {2,4,∞} {3,4} {3,4,2} {3,4,3} {3,4,4} {3,4,5} {3,4,6} {3,4,∞} {4,4} {4,4,2} {4,4,3} {4,4,4} {4,4,5} {4,4,6} {4,4,∞} {5,4} {5,4,2} {5,4,3} {5,4,4} {5,4,5} {5,4,6} {5,4,∞} {6,4} {6,4,2} {6,4,3} {6,4,4} {6,4,5} {6,4,6} {6,4,∞} {∞,4} {∞,4,2} {∞,4,3} {∞,4,4} {∞,4,5} {∞,4,6} {∞,4,∞}

{s,5,r} { p ,5} \ r 2 3 4 5 6 ∞ {2,5} {2,5,2} {2,5,3} {2,5,4} {2,5,5} {2,5,6} {2,5,∞} {3,5} {3,5,2} {3,5,3} {3,5,4} {3,5,5} {3,5,6} {3,5,∞} {4,5} {4,5,2} {4,5,3} {4,5,4} {4,5,5} {4,5,6} {4,5,∞} {5,5} {5,5,2} {5,5,3} {5,5,4} {5,5,5} {5,5,6} {5,5,∞} {6,5} {6,5,2} {6,5,3} {6,5,4} {6,5,5} {6,5,6} {6,5,∞} {∞,5} {∞,5,2} {∞,5,3} {∞,5,4} {∞,5,5} {∞,5,6} {∞,5,∞}

{s,6,r} { p ,6} \ r 2 3 4 5 6 ∞ {2,6} {2,6,2} {2,6,3} {2,6,4} {2,6,5} {2,6,6} {2,6,∞} {3,6} {3,6,2} {3,6,3} {3,6,4} {3,6,5} {3,6,6} {3,6,∞} {4,6} {4,6,2} {4,6,3} {4,6,4} {4,6,5} {4,6,6} {4,6,∞} {5,6} {5,6,2} {5,6,3} {5,6,4} {5,6,5} {5,6,6} {5,6,∞} {6,6} {6,6,2} {6,6,3} {6,6,4} {6,6,5} {6,6,6} {6,6,∞} {∞,6} {∞,6,2} {∞,6,3} {∞,6,4} {∞,6,5} {∞,6,6} {∞,6,∞}

{ p ,7, r } { p ,7} \ r 2 3 4 5 6 ∞ {2,7} {2,7,2} {2,7,3} {2,7,4} {2,7,5} {2,7,6} {2,7,∞} {3,7} {3,7,2} {3,7,3} {3,7,4} {3,7,5} {3,7,6} {3,7,∞} {4,7} {4,7,2} {4,7,3} {4,7,4} {4,7,5} {4,7,6} {4,7,∞} {5,7} {5,7,2} {5,7,3} {5,7,4} {5,7,5} {5,7,6} {5,7,∞} {6,7} {6,7,2} {6,7,3} {6,7,4} {6,7,5} {6,7,6} {6,7,∞} {∞,7} {∞,7,2} {∞,7,3} {∞,7,4} {∞,7,5} {∞,7,6} {∞,7,∞}

{s,8,r} { p ,8} \ r 2 3 4 5 6 ∞ {2,8} {2,8,2} {2,8,3} {2,8,4} {2,8,5} {2,8,6} {2,8,∞} {3,8} {3,8,2} {3,8,3} {3,8,4} {3,8,5} {3,8,6} {3,8,∞} {4,8} {4,8,2} {4,8,3} {4,8,4} {4,8,5} {4,8,6} {4,8,∞} {5,8} {5,8,2} {5,8,3} {5,8,4} {5,8,5} {5,8,6} {5,8,∞} {6,8} {6,8,2} {6,8,3} {6,8,4} {6,8,5} {6,8,6} {6,8,∞} {∞,8} {∞,8,2} {∞,8,3} {∞,8,4} {∞,8,5} {∞,8,6} {∞,8,∞}

{p,∞,r} { p ,∞} \ r 2 3 4 5 6 ∞ {2,∞} {2,∞,2} {2,∞,3} {2,∞,4} {2,∞,5} {2,∞,6} {2,∞,∞} {3,∞} {3,∞,2} {3,∞,3} {3,∞,4} {3,∞,5} {3,∞,6} {3,∞,∞} {4,∞} {4,∞,2} {4,∞,3} {4,∞,4} {4,∞,5} {4,∞,6} {4,∞,∞} {5,∞} {5,∞,2} {5,∞,3} {5,∞,4} {5,∞,5} {5,∞,6} {5,∞,∞} {6,∞} {6,∞,2} {6,∞,3} {6,∞,4} {6,∞,5} {6,∞,6} {6,∞,∞} {∞,∞} {∞,∞,2} {∞,∞,3} {∞,∞,4} {∞,∞,5} {∞,∞,6} {∞,∞,∞}

Det finns inga vanliga hyperboliska stjärnbikakor i H ³ : alla former med en vanlig stjärnpolyeder som cell, vertexfigur eller båda blir sfäriska.

Idealiska hörn uppträder nu när vertexfiguren är en euklidisk plattsättning, som blir inskrivbar i en horosfär snarare än en sfär. De är dubbla till ideala celler (euklidiska plattsättningar snarare än ändliga polyedrar). När den sista siffran i Schläfli-symbolen stiger ytterligare, blir vertexfiguren hyperbolisk, och hörn blir ultraideal (så att kanterna inte möts inom hyperboliskt utrymme). I honeycombs {p, q, ∞} skär kanterna Poincaré-kulan endast i en ideal punkt; resten av kanten har blivit ultra-ideal. Att fortsätta vidare skulle leda till kanter som är helt ultraidealiska, både för honungskakan och för den fundamentala simplexen (även om fortfarande oändligt många {p, q} skulle mötas vid sådana kanter). I allmänhet, när den sista siffran på Schläfli-symbolen blir ∞, skär ytor av kodimension två Poincaré-hyperbollen endast i en ideal punkt.

Fyra dimensioner (5-apeirotoper)

Tessellations av euklidiskt 4-rum

Det finns tre typer av oändliga regelbundna tesseller ( bikakor ) som kan tessellate euklidiskt fyrdimensionellt utrymme:

3 vanliga euklidiska honungskakor

namn	Schläfli -symbol {p,q,r,s}	Fasetttyp {p,q,r }	Celltyp {p,q }	Ansiktstyp { p}	Ansiktsfigur {s }	Kantfigur {r,s }	Hönsfigur {q,r , s}	Dubbel
Tesseraktisk honungskaka	{4,3,3,4}	{4,3,3}	{4,3}	{4}	{4}	{3,4}	{3,3,4}	Självdubbel
16-cells honungskaka	{3,3,4,3}	{3,3,4}	{3,3}	{3}	{3}	{4,3}	{3,4,3}	{3,4,3,3}
24-cells honungskaka	{3,4,3,3}	{3,4,3}	{3,4}	{3}	{3}	{3,3}	{4,3,3}	{3,3,4,3}

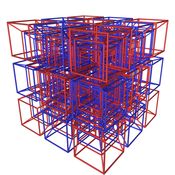Projicerad del av {4,3,3,4} (Tesseractic honeycomb)

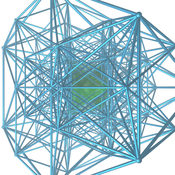Projicerad del av {3,3,4,3} (16-cells honungskaka)

Projicerad del av {3,4,3,3} (24-cells honungskaka)

Det finns också de två felaktiga fallen {4,3,4,2} och {2,4,3,4}.

Det finns tre platta regelbundna bikakor av Euklidisk 4-utrymme:

• {4,3,3,4}, {3,3,4,3} och {3,4,3,3}.

Det finns sju platta regelbundna konvexa bikakor med hyperboliskt 4-utrymme:

• 5 är kompakta: {3,3,3,5}, {5,3,3,3}, {4,3,3,5}, {5,3,3,4}, {5,3,3 ,5}
• 2 är parakompakta: {3,4,3,4} och {4,3,4,3}.

Det finns fyra platta regelbundna stjärnbikakor med hyperboliskt 4-rum:

• {5/2,5,3,3}, {3,3,5,5/2}, {3,5,5/2,5} och {5,5/2,5,3}.

Tessellations av hyperboliskt 4-mellanrum

Det finns sju konvexa vanliga bikakor och fyra stjärnbikakor i H ⁴ -utrymmet. Fem konvexa är kompakta och två är parakompakta.

Fem kompakta vanliga bikakor i H ⁴ :

5 kompakta vanliga honungskakor

namn	Schläfli -symbol {p,q,r,s}	Fasetttyp {p,q,r }	Celltyp {p,q }	Ansiktstyp { p}	Ansiktsfigur {s }	Kantfigur {r,s }	Hönsfigur {q,r , s}	Dubbel
Order-5 5-cells honungskaka	{3,3,3,5}	{3,3,3}	{3,3}	{3}	{5}	{3,5}	{3,3,5}	{5,3,3,3}
120-cells honungskaka	{5,3,3,3}	{5,3,3}	{5,3}	{5}	{3}	{3,3}	{3,3,3}	{3,3,3,5}
Order-5 tesseractic honeycomb	{4,3,3,5}	{4,3,3}	{4,3}	{4}	{5}	{3,5}	{3,3,5}	{5,3,3,4}
Order-4 120-cells honungskaka	{5,3,3,4}	{5,3,3}	{5,3}	{5}	{4}	{3,4}	{3,3,4}	{4,3,3,5}
Order-5 120-cells honungskaka	{5,3,3,5}	{5,3,3}	{5,3}	{5}	{5}	{3,5}	{3,3,5}	Självdubbel

De två parakompakta reguljära H ⁴ -bikakorna är: {3,4,3,4}, {4,3,4,3}.

2 parakompakta vanliga honungskakor

namn	Schläfli -symbol {p,q,r,s}	Fasetttyp {p,q,r }	Celltyp {p,q }	Ansiktstyp { p}	Ansiktsfigur {s }	Kantfigur {r,s }	Hönsfigur {q,r , s}	Dubbel
Order-4 24-cells honungskaka	{3,4,3,4}	{3,4,3}	{3,4}	{3}	{4}	{3,4}	{4,3,4}	{4,3,4,3}
Kubisk honeycomb honeycomb	{4,3,4,3}	{4,3,4}	{4,3}	{4}	{3}	{4,3}	{3,4,3}	{3,4,3,4}

Icke-kompakta lösningar existerar som Lorentzian Coxeter-grupper och kan visualiseras med öppna domäner i hyperboliskt utrymme (den grundläggande 5-cellen har vissa delar otillgängliga bortom oändligheten). Alla honungskakor som inte visas i tabelluppsättningen nedan och inte har 2 i sin Schläfli-symbol är icke-kompakta.

Sfäriska / euklidiska /hyperboliska ( kompakta / parakompakta / ickekompakta ) bikakor {p,q,r,s}
q=3, s=3 p \ r 3 4 5 3 {3,3,3,3} {3,3,4,3} {3,3,5,3} 4 {4,3,3,3} {4,3,4,3} {4,3,5,3} 5 {5,3,3,3} {5,3,4,3} {5,3,5,3}	q=3, s=4 p \ r 3 4 3 {3,3,3,4} {3,3,4,4} 4 {4,3,3,4} {4,3,4,4} 5 {5,3,3,4} {5,3,4,4}	q=3, s=5 p \ r 3 4 3 {3,3,3,5} {3,3,4,5} 4 {4,3,3,5} {4,3,4,5} 5 {5,3,3,5} {5,3,4,5}
q=4, s=3 p \ r 3 4 3 {3,4,3,3} {3,4,4,3} 4 {4,4,3,3} {4,4,4,3}	q=4, s=4 p \ r 3 4 3 {3,4,3,4} {3,4,4,4} 4 {4,4,3,4} {4,4,4,4}	q=4, s=5 p \ r 3 4 3 {3,4,3,5} {3,4,4,5} 4 {4,4,3,5} {4,4,4,5}
q=5, s=3 p \ r 3 4 3 {3,5,3,3} {3,5,4,3} 4 {4,5,3,3} {4,5,4,3}

Stjärntesselationer av hyperboliskt 4-mellanrum

Det finns fyra vanliga stjärnbikakor i H ⁴ -utrymmet, alla kompakta:

4 kompakta vanliga stjärnbikakor

namn	Schläfli -symbol {p,q,r,s}	Fasetttyp {p,q,r }	Celltyp {p,q }	Ansiktstyp { p}	Ansiktsfigur {s }	Kantfigur {r,s }	Hönsfigur {q,r , s}	Dubbel	Densitet
Liten stjärnformad 120-cells honungskaka	{5/2,5,3,3}	{5/2,5,3}	{5/2,5}	{5/2}	{3}	{3,3}	{5,3,3}	{3,3,5,5/2}	5
Pentagrammisk 600-cells honungskaka	{3,3,5,5/2}	{3,3,5}	{3,3}	{3}	{5/2}	{5,5/2}	{3,5,5/2}	{5/2,5,3,3}	5
Order-5 icosahedral 120-cells honungskaka	{3,5,5/2,5}	{3,5,5/2}	{3,5}	{3}	{5}	{5/2,5}	{5,5/2,5}	{5,5/2,5,3}	10
Fantastisk 120-cells honungskaka	{5,5/2,5,3}	{5,5/2,5}	{5,5/2}	{5}	{3}	{5,3}	{5/2,5,3}	{3,5,5/2,5}	10

Fem dimensioner (6-apeirotoper)

Det finns bara en platt vanlig bikaka av euklidiskt 5-utrymme: (tidigare listad ovan som tesseller)

• {4,3,3,3,4}

Det finns fem platta regelbundna bikakor med hyperboliska 5-mellanslag, alla parakompakta: (tidigare listade ovan som tesseller)

• {3,3,3,4,3}, {3,4,3,3,3}, {3,3,4,3,3}, {3,4,3,3,4} och { 4,3,3,4,3}

Tessellations av euklidiska 5-rymden

Den hyperkubiska honungskakan är den enda familjen av vanliga bikakor som kan tessellate varje dimension, fem eller högre, bildad av hyperkubfasetter , fyra runt varje ås .

namn	Schläfli { p 1 , p 2 , ..., p n −1 }	Fasetttyp _	Vertex figur	Dubbel
Fyrkantig plattsättning	{4,4}	{4}	{4}	Självdubbel
Kubisk honungskaka	{4,3,4}	{4,3}	{3,4}	Självdubbel
Tesseraktisk honungskaka	{4,3 2 ,4}	{4,3 2 }	{3 2 ,4}	Självdubbel
5-kuba honungskaka	{4,3 3 ,4}	{4,3 3 }	{3 3 ,4}	Självdubbel
6-kubbar honungskaka	{4,3 4 ,4}	{4,3 4 }	{3 4 ,4}	Självdubbel
7-kuba honungskaka	{4,3 5 ,4}	{4,3 5 }	{3 5 ,4}	Självdubbel
8-kubbar honungskaka	{4,3 6 ,4}	{4,3 6 }	{3 6 ,4}	Självdubbel
n- hyperkubisk honungskaka	{4,3 n−2 ,4}	{4,3 n−2 }	{3 n−2 ,4}	Självdubbel

I E ⁵ finns även de otillbörliga fallen {4,3,3,4,2}, {2,4,3,3,4}, {3,3,4,3,2}, {2,3 ,3,4,3}, {3,4,3,3,2} och {2,3,4,3,3}. I E ^{n är} {4,3 ⁿ⁻³ ,4,2} och {2,4,3 ^{n−3 ,} 4} alltid olämpliga euklidiska tessellationer.

Tessellationer av hyperboliskt 5-mellanslag

Det finns 5 vanliga bikakor i H ⁵ , alla parakompakta, som inkluderar oändliga (euklidiska) fasetter eller vertexfigurer: {3,4,3,3,3}, {3,3,4,3,3}, {3, 3,3,4,3}, {3,4,3,3,4} och {4,3,3,4,3}.

Det finns inga kompakta reguljära tessellationer av hyperboliskt utrymme av dimension 5 eller högre och inga parakompakta reguljära tessellationer i hyperboliskt utrymme av dimension 6 eller högre.

5 paracompact vanliga honungskakor

namn	Schläfli -symbol {p,q,r,s,t}	Fasetttyp {p,q,r , s}	4-ansiktstyp { p,q,r}	Celltyp {p,q }	Ansiktstyp { p}	Cellfigur { t}	Ansiktsfigur {s,t }	Kantfigur {r,s,t }	Hönsfigur {q,r,s , t}	Dubbel
5-ortoplex honungskaka	{3,3,3,4,3}	{3,3,3,4}	{3,3,3}	{3,3}	{3}	{3}	{4,3}	{3,4,3}	{3,3,4,3}	{3,4,3,3,3}
24-cells honeycomb honeycomb	{3,4,3,3,3}	{3,4,3,3}	{3,4,3}	{3,4}	{3}	{3}	{3,3}	{3,3,3}	{4,3,3,3}	{3,3,3,4,3}
16-cells honeycomb honeycomb	{3,3,4,3,3}	{3,3,4,3}	{3,3,4}	{3,3}	{3}	{3}	{3,3}	{4,3,3}	{3,4,3,3}	självdual
Order-4 24-cells honeycomb honeycomb	{3,4,3,3,4}	{3,4,3,3}	{3,4,3}	{3,4}	{3}	{4}	{3,4}	{3,3,4}	{4,3,3,4}	{4,3,3,4,3}
Tesseractic honeycomb honeycomb	{4,3,3,4,3}	{4,3,3,4}	{4,3,3}	{4,3}	{4}	{3}	{4,3}	{3,4,3}	{3,3,4,3}	{3,4,3,3,4}

Eftersom det inte finns några vanliga stjärn- n -polytoper för n ≥ 5, som kan vara potentiella celler eller vertexfigurer, finns det inga fler hyperboliska stjärnbikakor i H ⁿ för n ≥ 5.

6 dimensioner och högre (7-apeirotoper+)

Tessellationer av hyperboliskt 6-mellanslag och högre

Det finns inga vanliga kompakta eller parakompakta tesselleringar av hyperboliskt utrymme av dimension 6 eller högre. Alla Schläfli-symboler av formen {p,q,r,s,...} som inte täcks ovan (p,q,r,s,... naturliga tal över 2 eller oändlighet) kommer dock att bilda en icke-kompakt tessellation av hyperboliskt n -utrymme.

Sammansatta polytoper

Huvudartikel: Polytopförening

Tvådimensionella föreningar

För varje naturligt tal n finns det n-uddiga stjärnor med reguljära månghörniga stjärnor med Schläfli-symboler {n/m} för alla m så att m < n/2 (strängt taget {n/m}={n/(n−m) }) och m och n är coprime . När m och n inte är coprime, kommer den erhållna stjärnpolygonen att vara en vanlig polygon med n / m sidor. En ny siffra erhålls genom att rotera dessa regelbundna n / m -goner en vertex till vänster på den ursprungliga polygonen tills antalet roterade hörn är lika med n / m minus en, och kombinera dessa siffror. Ett extremfall av detta är när n / m är 2, vilket ger en siffra som består av n /2 räta linjesegment; detta kallas en degenererad stjärnpolygon .

I andra fall där n och m har en gemensam faktor , erhålls en stjärnpolygon för ett lägre n , och roterade versioner kan kombineras. Dessa figurer kallas stjärnfigurer , oegentliga stjärnpolygoner eller sammansatta polygoner . Samma notation { n / m } används ofta för dem, även om myndigheter som Grünbaum (1994) anser (med viss motivering) formen k { n } som mer korrekt, där vanligtvis k = m .

En ytterligare komplikation kommer när vi sammansätter två eller flera stjärnpolygoner, som till exempel två pentagram, som skiljer sig åt med en rotation på 36°, inskrivna i en dekagon. Detta är korrekt skrivet i formen k { n / m }, som 2{5/2}, snarare än det vanligaste {10/4}.

Coxeters utökade notation för föreningar är av formen c { m , n ,...}[ d { p , q ,...}] e { s , t ,...}, vilket indikerar att d distinkt { p , q ,...}s täcker tillsammans hörnen på { m , n ,...} c gånger och fasetterna av { s , t ,...} e gånger. Om det inte finns någon regelbunden { m , n ,...} tas den första delen av notationen bort och lämnar [ d { p , q ,...}] e { s , t ,...}; motsatsen gäller om inga vanliga { s , t ,...} existerar. Dualen av c { m , n ,...}[ d { p , q ,...}] e { s , t ,...} är e { t , s ,...}[ d { q , p ,...}] c { n , m ,...}. Om c eller e är 1 kan de utelämnas. För sammansatta polygoner reduceras denna notation till { nk }[ k { n / m }]{ nk }: till exempel kan hexagrammet skrivas som {6}[2{3}]{6}.

Exempel för n =2..10, nk ≤30

2{2}

3{2}

4{2}

5{2}

6{2}

7{2}

8{2}

9{2}

10{2}

11{2}

12{2}

13{2}

14{2}

15{2}

2{3}

3{3}

4{3}

5{3}

6{3}

7{3}

8{3}

9{3}

10{3}

2{4}

3{4}

4{4}

5{4}

6{4}

7{4}

2{5}

3{5}

4{5}

5{5}

6{5}

2{5/2}

3{5/2}

4{5/2}

5{5/2}

6{5/2}

2{6}

3{6}

4{6}

5{6}

2{7}

3{7}

4{7}

2{7/2}

3{7/2}

4{7/2}

2{7/3}

3{7/3}

4{7/3}

2{8}

3{8}

2{8/3}

3{8/3}

2{9}

3{9}

2{9/2}

3{9/2}

2{9/4}

3{9/4}

2{10}

3{10}

2{10/3}

3{10/3}

2{11}

2{11/2}

2{11/3}

2{11/4}

2{11/5}

2{12}

2{12/5}

2{13}

2{13/2}

2{13/3}

2{13/4}

2{13/5}

2{13/6}

2{14}

2{14/3}

2{14/5}

2{15}

2{15/2}

2{15/4}

2{15/7}

Regelbundna sneda polygoner skapar också sammansättningar, ses i kanterna av prismatisk sammansättning av antiprismor, till exempel:

Vanlig sammansatt sned polygon

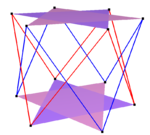
Sammansatt sneda rutor		Sammansatt skeva hexagoner	Sammansatta sneda dekagoner
Två {2}#{ }	Tre {2}#{ }	Två {3}#{ }	Två {5/3}#{ }

Tredimensionella föreningar

En vanlig polyederförening kan definieras som en förening som, liksom en vanlig polyeder, är vertextransitiv , kanttransitiv och ansiktstransitiv . Med denna definition finns det 5 vanliga föreningar.

Symmetri	[4,3], O h	[5,3] + , I	[5,3], I h
Dualitet	Självdubbel			Dubbla par
Bild
Sfärisk
Polyhedra	2 {3,3}	5 {3,3}	10 {3,3}	5 {4,3}	5 {3,4}
Coxeter	{4,3} [2 {3,3} ] {3,4}	{5,3} [5 {3,3} ] {3,5}	2 {5,3} [10 {3,3} ]2 {3,5}	2 {5,3} [5 {4,3} ]	[5 {3,4} ]2 {3,5}

Coxeters notation för vanliga föreningar ges i tabellen ovan, med Schläfli-symboler . Materialet innanför hakparenteserna, [ d { p , q }], betecknar komponenterna i föreningen: d separata { p , q }:s. Materialet före hakparenteserna betecknar föreningens vertexarrangemang: c { m , n }[ d { p , q }] är en förening av d { p , q } som delar hörnen på en { m , n } räknat c gånger. Materialet efter hakparenteserna anger fasettarrangemanget av föreningen: [ d { p , q }] e { s , t } är en sammansättning av d { p , q } som delar sidorna av { s , t } räknade e gånger. Dessa kan kombineras: sålunda c ​​{ m , n }[ d { p , q }] e { s , t } en sammansättning av d { p , q } som delar hörnen på { m , n } räknade c gånger och ansiktena på { s , t } räknade e gånger. Denna notation kan generaliseras till föreningar i valfritt antal dimensioner.

Euklidiska och hyperboliska planföreningar

Det finns arton tvåparameterfamiljer av vanliga sammansatta tesselleringar av det euklidiska planet. I det hyperboliska planet är fem enparameterfamiljer och sjutton isolerade fall kända, men fullständigheten i denna lista har ännu inte bevisats.

De euklidiska och hyperboliska sammansättningsfamiljerna 2 { p , p } (4 ≤ p ≤ ∞, p ett heltal) är analoga med den sfäriska stellan octangula , 2 {3,3}.

Några exempel på euklidiska och hyperboliska vanliga föreningar

Självdubbel	Dualer		Självdubbel
2 {4,4}	2 {6,3}	2 {3,6}	2 {∞,∞}
{{4,4}} eller a{4,4} eller {4,4}[2{4,4}]{4,4} + eller	[2{6,3}]{3,6}	a{6,3} eller {6,3}[2{3,6}] + eller	{{∞,∞}} eller a{∞,∞} eller {4,∞}[2{∞,∞}]{∞,4} + eller
	3 {6,3}	3 {3,6}	3 {∞,∞}
	2{3,6}[3{6,3}]{6,3}	{3,6}[3{3,6}]2{6,3} + +	+ +

Fyrdimensionella föreningar

Ortogonala projektioner

75 {4,3,3}	75 {3,3,4}

Coxeter listar 32 vanliga föreningar av vanliga 4-polytoper i sin bok Regular Polytopes . McMullen lägger till sex i sin artikel New Regular Compounds of 4-Polytopes, där han också bevisar att listan nu är komplett. I följande tabeller indikerar det upphöjda (var) att de märkta föreningarna skiljer sig från de andra föreningarna med samma symboler.

Självdubbla reguljära föreningar

Förening	Konstituerande	Symmetri	Vertex arrangemang	Cellarrangemang
120 {3,3,3}	5-cell	[5,3,3], order 14400	{5,3,3}	{3,3,5}
120 {3,3,3} (var)	5-cell	beställ 1200	{5,3,3}	{3,3,5}
720 {3,3,3}	5-cell	[5,3,3], order 14400	6{5,3,3}	6{3,3,5}
5 {3,4,3}	24-celler	[5,3,3], order 14400	{3,3,5}	{5,3,3}

Vanliga föreningar som dubbla par

Förening 1	Förening 2	Symmetri	Vertex arrangemang (1)	Cellarrangemang (1)	Vertex arrangemang (2)	Cellarrangemang (2)
3 {3,3,4}	3 {4,3,3}	[3,4,3], order 1152	{3,4,3}	2{3,4,3}	2{3,4,3}	{3,4,3}
15 {3,3,4}	15 {4,3,3}	[5,3,3], order 14400	{3,3,5}	2{5,3,3}	2{3,3,5}	{5,3,3}
75 {3,3,4}	75 {4,3,3}	[5,3,3], order 14400	5{3,3,5}	10{5,3,3}	10{3,3,5}	5{5,3,3}
75 {3,3,4}	75 {4,3,3}	[5,3,3], order 14400	{5,3,3}	2{3,3,5}	2{5,3,3}	{3,3,5}
75 {3,3,4}	75 {4,3,3}	beställ 600	{5,3,3}	2{3,3,5}	2{5,3,3}	{3,3,5}
300 {3,3,4}	300 {4,3,3}	[5,3,3] + , order 7200	4{5,3,3}	8{3,3,5}	8{5,3,3}	4{3,3,5}
600 {3,3,4}	600 {4,3,3}	[5,3,3], order 14400	8{5,3,3}	16{3,3,5}	16{5,3,3}	8{3,3,5}
25 {3,4,3}	25 {3,4,3}	[5,3,3], order 14400	{5,3,3}	5{5,3,3}	5{3,3,5}	{3,3,5}

Det finns två olika sammansättningar av 75 tesserakter: en delar hörn på en 120-cells, medan den andra delar hörn på en 600-cell. Det följer därför omedelbart att de motsvarande dubbla föreningarna av 75 16-celler också är olika.

Självdubbla stjärnföreningar

Förening	Symmetri	Vertex arrangemang	Cellarrangemang
5 {5,5/2,5}	[5,3,3] + , order 7200	{5,3,3}	{3,3,5}
10 {5,5/2,5}	[5,3,3], order 14400	2{5,3,3}	2{3,3,5}
5 {5/2,5,5/2}	[5,3,3] + , order 7200	{5,3,3}	{3,3,5}
10 {5/2,5,5/2}	[5,3,3], order 14400	2{5,3,3}	2{3,3,5}

Vanliga stjärnföreningar som dubbla par

Förening 1	Förening 2	Symmetri	Vertex arrangemang (1)	Cellarrangemang (1)	Vertex arrangemang (2)	Cellarrangemang (2)
5 {3,5,5/2}	5 {5/2,5,3}	[5,3,3] + , order 7200	{5,3,3}	{3,3,5}	{5,3,3}	{3,3,5}
10 {3,5,5/2}	10 {5/2,5,3}	[5,3,3], order 14400	2{5,3,3}	2{3,3,5}	2{5,3,3}	2{3,3,5}
5 {5,5/2,3}	5 {3,5/2,5}	[5,3,3] + , order 7200	{5,3,3}	{3,3,5}	{5,3,3}	{3,3,5}
10 {5,5/2,3}	10 {3,5/2,5}	[5,3,3], order 14400	2{5,3,3}	2{3,3,5}	2{5,3,3}	2{3,3,5}
5 {5/2,3,5}	5 {5,3,5/2}	[5,3,3] + , order 7200	{5,3,3}	{3,3,5}	{5,3,3}	{3,3,5}
10 {5/2,3,5}	10 {5,3,5/2}	[5,3,3], order 14400	2{5,3,3}	2{3,3,5}	2{5,3,3}	2{3,3,5}

Det finns också fjorton delvis regelbundna föreningar, som antingen är vertextransitiva eller celltransitiva men inte båda. De sju vertextransitiva partiellt regelbundna föreningarna är dualerna av de sju celltransitiva partiellt regelbundna föreningarna.

Delvis regelbundna föreningar som dubbla par

Förening 1 Vertex-transitiv	Förening 2 Celltransitiv	Symmetri
2 16-celler	2 tesserakter	[4,3,3], order 384
25 24-celler (var)	25 24-celler (var)	beställ 600
100 24-celler	100 24-celler	[5,3,3] + , order 7200
200 24-celler	200 24-celler	[5,3,3], order 14400
5 600-celler	5 120-celler	[5,3,3] + , order 7200
10 600-celler	10 120-cell	[5,3,3], order 14400

Delvis regelbundna stjärnföreningar som dubbla par

Förening 1 Vertex-transitiv	Förening 2 Celltransitiv	Symmetri
5 {3,3,5/2}	5 {5/2,3,3}	[5,3,3] + , order 7200
10 {3,3,5/2}	10 {5/2,3,3}	[5,3,3], order 14400

Även om 5-cells- och 24-cellerna båda är självdubbla, anses deras dubbla föreningar (sammansättningen av två 5-celler och sammansättningen av två 24-celler) inte vara regelbundna, till skillnad från sammansättningen av två tetraedrar och de olika dubbla polygonföreningar, eftersom de varken är vertexregelbundna eller cellregelbundna: de är inte fasetteringar eller stellationer av någon vanlig 4-polytop. De är dock vertex-, kant-, ansikts- och celltransitiva.

Euklidiska 3-rumsföreningar

De enda vanliga euklidiska sammansatta bikakorna är en oändlig familj av föreningar av kubiska vaxkakor , som alla delar hörn och ansikten med en annan kubisk vaxkaka. Denna förening kan ha hur många kubiska bikakor som helst. Coxeter-notationen är {4,3,4}[ d {4,3,4}]{4,3,4}.

Fem dimensioner och högre föreningar

Det finns inga vanliga föreningar i fem eller sex dimensioner. Det finns tre kända sjudimensionella föreningar (16, 240 eller 480 7-simplicerade ) och sex kända åttadimensionella (16, 240 eller 480 8-kuber eller 8-ortoplexer ). Det finns också en sammansättning av n -simplicerar i n -dimensionellt rymden förutsatt att n är en mindre än en potens av två, och även två sammansättningar (en av n -kuber och en dubbel av n -ortoplexer) i n -dimensionella rymden om n är en potens av två.

Coxeter-notationen för dessa föreningar är (med α ⁿ = {3 ^{n −1} }, β ⁿ = {3 ^{n −2} ,4}, γ _n = {4,3 ^{n −2} }):

• 7-simplex: c γ ₇ [16 c α ₇ ] c β ₇ , där c = 1, 15 eller 30
• 8-ortoplexer: c γ ₈ [16 c β ₈ ]
• 8-kuber: [16 c γ ₈ ] c β ₈

De allmänna fallen (där n = 2 ^k och d = 2 ^{2 k − k − 1} , k = 2, 3, 4, ...):

• Simplex: γ _{n −1} [ d α _{n −1} ]β _{n −1}
• Ortoplexer: γ _n [ d β _n ]
• Hyperkuber: [ d γ _n ]β _n

Euklidiska bikakeföreningar

En känd familj av vanliga euklidiska sammansatta honeycombs i fem eller fler dimensioner är en oändlig familj av sammansättningar av hyperkubiska honeycombs , som alla delar hörn och ansikten med en annan hyperkubisk honeycomb. Denna förening kan ha hur många hyperkubiska bikakor som helst. Coxeter-notationen är δ _n [ d δ _n ]δ _n där δ _n = {∞} när n = 2 och {4,3 ^{n −3} ,4} när n ≥ 3.

Abstrakta polytoper

De abstrakta polytoperna uppstod ur ett försök att studera polytoper bortsett från det geometriska rummet de är inbäddade i. De inkluderar tessellationerna av sfäriskt, euklidiskt och hyperboliskt rum, tessellations av andra grenrör och många andra objekt som inte har en väldefinierad topologi, men kan istället kännetecknas av sin "lokala" topologi. Det finns oändligt många i varje dimension. Se denna atlas för ett exempel. Några anmärkningsvärda exempel på abstrakta reguljära polytoper som inte förekommer någon annanstans i den här listan är 11-cellen , {3,5,3} och 57-cellen , {5,3,5}, som har regelbundna projektiva polyedrar som celler och vertexfigurer.

Elementen i en abstrakt polyeder är dess kropp (det maximala elementet), dess ytor, kanter, hörn och nollpolytopen eller den tomma mängden. Dessa abstrakta element kan mappas in i det vanliga rummet eller realiseras som geometriska figurer. Vissa abstrakta polyedrar har välformade eller trogna insikter, andra inte. En flagga är en sammankopplad uppsättning element av varje dimension - för en polyeder som är kroppen, ett ansikte, en kant av ansiktet, en spets på kanten och nollpolytopen. En abstrakt polytop sägs vara regelbunden om dess kombinatoriska symmetrier är transitiva på dess flaggor - det vill säga att vilken flagga som helst kan mappas till vilken som helst annan under polyederns symmetri. Abstrakta vanliga polytoper är fortfarande ett aktivt forskningsområde.

Fem sådana reguljära abstrakta polyedrar, som inte kan realiseras troget, identifierades av HSM Coxeter i hans bok Regular Polytopes (1977) och återigen av JM Wills i hans artikel "The combinatorially regular polyhedra of index 2" (1987). De är alla topologiskt likvärdiga med toroider . Deras konstruktion, genom att arrangera n ansikten runt varje vertex, kan upprepas i det oändliga som plattsättningar av det hyperboliska planet . I diagrammen nedan har de hyperboliska plattsättningsbilderna färger som motsvarar de på polyedrbilderna.

Polyeder	Medial rombisk triacontahedron	Dodecadodecahedron	Medial triambisk ikosaeder	Ditrigonal dodecadodecahedron	Utgrävd dodekaeder
Vertex figur	{5}, {5/2}	(5,5/2) 2	{5}, {5/2}	(5,5/3) 3
Ansikten	30 rhombi	12 pentagoner 12 pentagram	20 hexagoner	12 pentagoner 12 pentagram	20 hexagram
Kakelsättning	{4, 5}	{5, 4}	{6, 5}	{5, 6}	{6, 6}
χ	−6	−6	−16	−16	−20

Dessa förekommer som dubbla par enligt följande:

• Den mediala rombiska triacontahedron och dodecadodecahedron är dubbla till varandra.
• Den mediala triambiska icosaedern och ditrigonala dodecadodecahedron är dubbla till varandra.
• Den utgrävda dodekaedern är självdual.

Se även

• Polygon
  • Vanlig polygon
  • Stjärnpolygon
• Polyeder
  • Vanlig polyeder (5 vanliga platonska fasta ämnen och 4 Kepler-Poinsot fasta ämnen )
    • Uniform polyeder
  • Petrial
• 4-polytop
  • Vanlig 4-polytop (16 vanliga 4-polytoper, 4 konvexa och 10 stjärniga (Schläfli–Hess))
  • Uniform 4-polytop
• Tessellation
  • Plattläggning av vanliga polygoner
  • Konvex enhetlig honungskaka
• Vanlig polytop
  • Uniform polytop
• Vanlig karta (grafteori)

Anteckningar

•     Coxeter, HSM (1999), "Kapitel 10: Regular Honeycombs in Hyperbolic Space", The Beauty of Geometry: Twelve Essays , Mineola, NY: Dover Publications, Inc., s. 199–214, ISBN 0-486-40919-8 , LCCN 99035678 , MR 1717154 . Se särskilt sammanfattningstabellerna II,III,IV,V, s. 212–213.
  • Ursprungligen publicerad i   Coxeter, HSM (1956), "Regular honeycombs in hyperbolic space" (PDF) , Proceedings of the International Congress of Mathematicians, 1954, Amsterdam , vol. III, Amsterdam: North-Holland Publishing Co., s. 155–169, MR 0087114 , arkiverad från originalet (PDF) 2015-04-02 .
•     Coxeter, HSM (1973) [1948]. Regular Polytopes (tredje upplagan). New York: Dover Publications. ISBN 0-486-61480-8 . MR 0370327 . OCLC 798003 . Se särskilt tabellerna I och II: Regelbundna polytoper och honeycombs, s. 294–296.
• Johnson, Norman W. (2012), "Regular inversive polytopes" (PDF) , International Conference on Mathematics of Distances and Applications (2–5 juli 2012, Varna, Bulgarien) , s. 85–95 Paper 27
•    McMullen, Peter ; Schulte, Egon (2002), Abstract Regular Polytopes , Encyclopedia of Mathematics and its Applications, vol. 92, Cambridge: Cambridge University Press, doi : 10.1017/CBO9780511546686 , ISBN 0-521-81496-0 , MR 1965665
•   McMullen, Peter (2018), "New Regular Compounds of 4-Polytopes", New Trends in Intuitive Geometry , Bolyai Society Mathematical Studies, 27 : 307–320, doi : 10.1007/978-3-662-574913 , 8_SBN 7-3_ -3-662-57412-6 .
• Nelson, Roice; Segerman , Henry (2015). "Visualisera hyperboliska honungskakor". arXiv : 1511.02851 [ math.HO ]. hyperbolichoneycombs.org/
•   Sommerville, DMY (1958), An Introduction to the Geometry of n Dimensions , New York: Dover Publications, Inc., MR 0100239 . Omtryck av 1930 års upplaga, utgiven av EP Dutton. Se särskilt kapitel X: De vanliga polytoperna.

externa länkar

• De platonska kropparna
• Kepler-Poinsot polyeder
• Vanliga 4d Polytope utfällbara
• Flerdimensionell ordlista (Slå upp Hexacosichoron och Hecatonicosachoron )
• Polytope Viewer
• Polytoper och optimal packning av p-punkter i n-dimensionella sfärer
• En atlas över små vanliga polytoper
• Regelbundna polyedrar genom tiden I. Hubard, Polytopes, Maps and their Symmetries
• Regular Star Polytopes , Nan Ma

Grundläggande konvexa regelbundna och enhetliga bikakor i dimensionerna 2–9
Plats	Familj	${\tilde {A}}_{n-1}$	${\tilde {C}}_{n-1}$	${\tilde {B}}_{n-1}$	${\tilde {D}}_{n-1}$	${\tilde {G}}_{2}$ / ${\tilde {F}}_{4}$ / ${\tilde { E}}_{n-1}$
E 2	Enhetlig plattsättning	{3 [3] }	δ 3	hδ 3	qδ 3	Hexagonal
E 3	Enhetlig konvex bikaka	{3 [4] }	δ 4	hδ 4	qδ 4
E 4	Uniform 4-honeycomb	{3 [5] }	δ 5	hδ 5	qδ 5	24-cells honungskaka
E 5	Uniform 5-bikaka	{3 [6] }	δ 6	hδ 6	qδ 6
E 6	Uniform 6-honeycomb	{3 [7] }	δ 7	hδ 7	qδ 7	2 22
E 7	Uniform 7-honeycomb	{3 [8] }	δ 8	hδ 8	qδ 8	1 33 • 3 31
E 8	Uniform 8-honeycomb	{3 [9] }	δ 9	hδ 9	qδ 9	1 52 • 2 51 • 5 21
E 9	Uniform 9-honeycomb	{3 [10] }	δ 10	hδ 10	qδ 10
E 10	Uniform 10-honeycomb	{3 [11] }	δ 11	hδ 11	qδ 11
E n -1	Uniform ( n -1)- honeycomb	{3 [n] }	5 n	hδ n	qδ n	1 k2 • 2 k1 • k 21