Order-7 tetraedrisk honungskaka
| Order-7 tetraedrisk honungskaka | |
|---|---|
| Typ | Hyperbolisk vanlig honungskaka |
| Schläfli symboler | {3,3,7} |
| Coxeter diagram |
   
|
| Celler |
{3,3} 
|
| Ansikten | {3} |
| Kantfigur | {7} |
| Vertex figur |
{3,7} 
|
| Dubbel | {7,3,3} |
| Coxeter grupp | [7,3,3] |
| Egenskaper | Regelbunden |
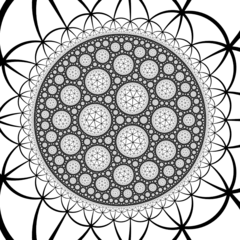
I geometrin för hyperboliskt 3-rum är den tetraedriska bikakan av order-7 en vanlig rymdfyllande tessellation (eller honeycomb ) med Schläfli-symbolen {3,3,7}. Den har sju tetraedrar {3,3} runt varje kant. Alla hörn är ultra-ideala (existerar bortom den ideala gränsen) med oändligt många tetraedrar som existerar runt varje vertex i ett triangulärt arrangemang av 7 triangulära sidor .
Bilder
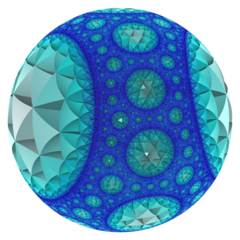 Poincaré diskmodell (cellcentrerad) |
 Gjort genomskärning av honeycomb med det idealiska planet i Poincaré halvrymdsmodell |
Besläktade polytoper och bikakor
Det är en del av en sekvens av vanliga polychora och honungskakor med tetraedriska celler , {3,3, p }.
| {3,3,p} polytoper | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Plats | S 3 | H 3 | |||||||||
| Form | Ändlig | Paracompact | Icke-kompakt | ||||||||
| namn |
{3,3,3}
|
{3,3,4}  
|
{3,3,5}
|
{3,3,6} 
|
{3,3,7}
|
{3,3,8} 
|
... {3,3,∞}  
|
||||
| Bild |
|
|
|
|
|
|
|
||||
|
Vertex figur |
 {3,3}
|
 {3,4}
|
 {3,5}
|
 {3,6}
|
{3,7}
|
 {3,8}
|
 {3,∞}
|
||||
Det är en del av en sekvens av hyperboliska bikakor med ordning-7 triangulära tegelformade vertexfigurer, { p ,3,7}.
| {3,3,7} | {4,3,7} | {5,3,7} | {6,3,7} | {7,3,7} | {8,3,7} | {∞,3,7} |
|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
Det är en del av en sekvens av hyperboliska bikakor, {3, p ,7}.
Order-8 tetraedrisk honungskaka
| Order-8 tetraedrisk honungskaka | |
|---|---|
| Typ | Hyperbolisk vanlig honungskaka |
| Schläfli symboler |
{3,3,8} {3,(3,4,3)} |
| Coxeter diagram |
 =
|
| Celler |
{3,3}
|
| Ansikten | {3} |
| Kantfigur | {8} |
| Vertex figur |
{3,8} {(3,4,3)} 
|
| Dubbel | {8,3,3} |
| Coxeter grupp |
[3,3,8] [3,((3,4,3))] |
| Egenskaper | Regelbunden |
I geometrin för hyperboliskt 3-rum är den tetraedriska bikakan av order-8 en vanlig rymdfyllande tessellation (eller honeycomb ) med Schläfli-symbolen {3,3,8}. Den har åtta tetraedrar {3,3} runt varje kant. Alla hörn är ultra-ideala (existerar bortom den ideala gränsen) med oändligt många tetraedrar som finns runt varje vertex i ett triangulärt arrangemang av 8-triangulära hörn .
|
Poincaré diskmodell (cellcentrerad) |
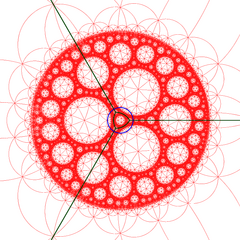 Gjort genomskärning av honeycomb med det ideala planet i Poincaré halvrymdsmodell |
Den har en andra konstruktion som en enhetlig bikaka, Schläfli-symbol {3,(3,4,3)}, Coxeter-diagram, , med alternerande typer eller färger av tetraedriska celler. I Coxeter-notation är halvsymmetrin [3,3,8,1 + ] = [3,((3,4,3))].
Oändlig ordning tetraedrisk honungskaka
| Oändlig ordning tetraedrisk honungskaka | |
|---|---|
| Typ | Hyperbolisk vanlig honungskaka |
| Schläfli symboler |
{3,3,∞} {3,(3,∞,3)} |
| Coxeter diagram |
=
|
| Celler |
{3,3}
|
| Ansikten | {3} |
| Kantfigur | {∞} |
| Vertex figur |
{3,∞} {(3,∞,3)} 
|
| Dubbel | {∞,3,3} |
| Coxeter grupp |
[∞,3,3] [3,((3,∞,3))] |
| Egenskaper | Regelbunden |
I geometrin av hyperboliskt 3-rum är den oändliga ordningens tetraedriska honungskakan en vanlig rymdfyllande tessellation (eller honeycomb ) med Schläfli-symbolen {3,3,∞}. Den har oändligt många tetraedrar {3,3} runt varje kant. Alla hörn är ultra-ideala (existerar bortom den ideala gränsen) med oändligt många tetraedrar som existerar runt varje vertex i ett arrangemang av oändlig ordning .
|
Poincaré diskmodell (cellcentrerad) |
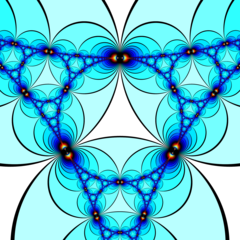 Gjort genomskärning av honeycomb med det idealiska planet i Poincaré halvrymdsmodell |
Den har en andra konstruktion som en enhetlig bikaka, Schläfli-symbol {3,(3,∞,3)}, Coxeter-diagram, = , med alternerande typer eller färger av tetraedriska celler. I Coxeter-notation är halvsymmetrin [3,3,∞,1 + ] = [3,((3,∞,3))].
Se även
- Coxeter , Regular Polytopes , 3:a. ed., Dover Publications, 1973. ISBN 0-486-61480-8 . (Tabell I och II: Vanliga polytoper och honeycombs, s. 294–296)
- The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN 99-35678 , ISBN 0-486-40919-8 (Kapitel 10, Regular Honeycombs in Hyperbolic Space ) Tabell III
- Jeffrey R. Weeks The Shape of Space, 2:a upplagan ISBN 0-8247-0709-5 (kapitel 16–17: Geometries on Three-manifolds I,II)
- George Maxwell, Sphere Packings and Hyperbolic Reflection Groups , JOURNAL OF ALGEBRA 79,78-97 (1982) [1]
- Hao Chen, Jean-Philippe Labbé, Lorentzian Coxeter-grupper och Boyd-Maxwell bollpackningar , (2013) [2]
- Visualisera hyperboliska honeycombs arXiv:1511.02851 Roice Nelson, Henry Segerman (2015)
externa länkar
- John Baez , Visuella insikter : {7,3,3} Honeycomb (2014/08/01) {7,3,3} Honeycomb Meets Plane at Infinity (2014/08/14)
- Danny Calegari , Kleinian, ett verktyg för att visualisera Kleinian-grupper, Geometry and the Imagination 4 mars 2014. [3]