Fyrkantig kakelkaka

Se även: Order-4 fyrkantig kakel honeycomb

Fyrkantig kakelkaka
Typ	Hyperbolisk vanlig honeycomb Paracompact enhetlig honeycomb
Schläfli symboler	{4,4,3} r{4,4,4} {4 1,1,1 }
Coxeter diagram	↔ ↔ ↔
Celler	{4,4}
Ansikten	kvadrat {4}
Kantfigur	triangel {3}
Vertex figur	kub , {4,3}
Dubbel	Order-4 oktaedrisk honungskaka
Coxeter grupper	${\overline {R}}_{3}$ , [4,4,3] ${\overline {N}}_{3}$ , [4 3 ] ${\overline {M}}_{3}$ , [4 1,1,1 ]
Egenskaper	Regelbunden

I geometrin med hyperbolisk 3-mellanrum är den fyrkantiga bikakan med kakel en av 11 parakompakta vanliga bikakor. Det kallas paracompact eftersom det har oändliga celler , vars hörn finns på horosfärer och konvergerar till en enda idealpunkt i oändligheten. Givet av Schläfli-symbolen {4,4,3} har den tre kvadratiska plattsättningar , {4,4}, runt varje kant, och sex kvadratiska plattsättningar runt varje vertex, i en kubisk {4,3} vertexfigur .

En geometrisk bikaka är en rymdfyllning av polyedriska eller högre dimensionella celler , så att det inte finns några luckor. Det är ett exempel på den mer allmänna matematiska plattsättningen eller tessellationen i valfritt antal dimensioner.

Bikakor konstrueras vanligtvis i vanligt euklidiskt ("platt") utrymme, som de konvexa enhetliga bikakorna . De kan också konstrueras i icke-euklidiska utrymmen , såsom hyperboliska enhetliga honeycombs . Vilken ändlig enhetlig polytop som helst kan projiceras till sin omkrets för att bilda en enhetlig bikaka i sfäriskt utrymme.

Rättad order-4 kvadratisk plattsättning

Den ses också som en korrigerad ordning-4 fyrkantig bikaka med kakel, r{4,4,4}:

{4,4,4}	r{4,4,4} = {4,4,3}
	=

Symmetri

Den fyrkantiga kakelbikakan har tre reflekterande symmetrikonstruktioner: som en vanlig bikaka, en halvsymmetrikonstruktion ↔ , och slutligen en konstruktion med tre typer (färger) av rutiga fyrkantiga plattor ↔ .

Den innehåller också en index 6-undergrupp [4,4,3 ^* ] ↔ [4 ^1,1,1 ] och en radiell undergrupp [4,(4,3) ^* ] av index 48, med en rätvinklig oktaedral fundamental domän och fyra par ultraparallella speglar: .

Denna honeycomb innehåller 2- hypercykelytor , som liknar paracompact order-3 apeirogonal plattsättning :

Besläktade polytoper och bikakor

Den fyrkantiga bikakan är en vanlig hyperbolisk vaxkaka i 3-utrymmen. Det är en av elva vanliga paracompact honeycombs.

Det finns femton enhetliga bikakor i [4,4,3] Coxeter- gruppfamiljen, inklusive denna vanliga form, och dess dubbla , den oktaedriska bikakan av ordningen-4 , {3,4,4}.

[4,4,3] familjens honungskakor

{4,4,3}	r{4,4,3}	t{4,4,3}	rr{4,4,3}	t 0,3 {4,4,3}	tr{4,4,3}	t 0,1,3 {4,4,3}	t 0,1,2,3 {4,4,3}
{3,4,4}	r{3,4,4}	t{3,4,4}	rr{3,4,4}	2t{3,4,4}	tr{3,4,4}	t 0,1,3 {3,4,4}	t 0,1,2,3 {3,4,4}

Den fyrkantiga honeycomb-kakeln är en del av den fyrkantiga honeycomb- familjen i order-4, eftersom den kan ses som en korrigerad order-4 fyrkantig honeycomb.

Det är relaterat till 24-cellen , {3,4,3}, som också har en kubisk vertexfigur. Det är också en del av en sekvens av bikakor med kvadratiska kakelceller:

{4,4,p} honungskakor
Plats	E 3	H 3
Form	Affine	Paracompact		Icke-kompakt
namn	{4,4,2}	{4,4,3}	{4,4,4}	{4,4,5}	{4,4,6}	... {4,4,∞}
Coxeter
bild
Vertex figur	{4,2}	{4,3}	{4,4}	{4,5}	{4,6}	{4,∞}

Riktad fyrkantig kakelkaka

Riktad fyrkantig kakelkaka
Typ	Paracompact uniform honeycomb Halvregelbunden honeycomb
Schläfli symboler	r{4,4,3} eller t 1 {4,4,3} 2r{3,4 1,1 } r{4 1,1,1 }
Coxeter diagram	↔ ↔ ↔
Celler	{4,3} r{4,4}
Ansikten	kvadrat {4}
Vertex figur	trekantsprisma
Coxeter grupper	${\overline {R}}_{3}$ , [4,4,3] ${\overline {O}}_{3}$ , [3,4 1 ,1 ] ${\overline {M}}_{3}$ , [4 1,1,1 ]
Egenskaper	Vertextransitiv, kanttransitiv

Den rätade, fyrkantiga bikakan , t ₁ {4,4,3}, har kub- och fyrkantiga kakelfasetter, med en triangulär prisma vertexfigur .

Det liknar den 2D-hyperboliska enhetliga triapeirogonala plattsättningen , r{∞,3}, med triangel- och apeirogonala ytor.

Stympad fyrkantig kakelkaka

Stympad fyrkantig kakelkaka
Typ	Paracompact enhetlig honeycomb
Schläfli symboler	t{4,4,3} eller t 0,1 {4,4,3}
Coxeter diagram	↔ ↔
Celler	{4,3} t{4,4}
Ansikten	fyrkantig {4} oktagon {8}
Vertex figur	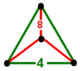triangulär pyramid
Coxeter grupper	${\overline {R}}_{3}$ , [4,4,3] ${\overline {N}}_{3}$ , [4 3 ] ${\overline {M}}_{3}$ , [4 1,1,1 ]
Egenskaper	Vertex-transitiv

Den avkortade fyrkantiga bikakan , t{4,4,3}, har kub och avkortade fyrkantiga kakelfasetter, med en triangulär pyramidformad vertexfigur . Det är samma som den cantitruncated order-4 fyrkantiga tegel honeycomb , tr{4,4,4}, .

Bitruncated fyrkantigt kakel bikaka

Bitruncated fyrkantigt kakel bikaka
Typ	Paracompact enhetlig honeycomb
Schläfli symboler	2t{4,4,3} eller t 1,2 {4,4,3}
Coxeter diagram
Celler	t{4,3} t{4,4}
Ansikten	triangel {3} kvadratisk {4} oktagon {8}
Vertex figur	digonal disfenoid
Coxeter grupper	${\overline {R}}_{3}$ , [4,4,3]
Egenskaper	Vertex-transitiv

Den bitrunkerade fyrkantiga bikakan , 2t{4,4,3}, har trunkerade kuber och trunkerade fyrkantiga kakelfasetter, med en digonal disfenoid vertexfigur .

Kantellerat fyrkantigt kakel bikaka

Kantellerat fyrkantigt kakel bikaka
Typ	Paracompact enhetlig honeycomb
Schläfli symboler	rr{4,4,3} eller t 0,2 {4,4,3}
Coxeter diagram	↔
Celler	r{4,3} rr{4,4} {}x{3}
Ansikten	triangel {3} kvadrat {4}
Vertex figur	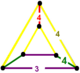likbent triangulärt prisma
Coxeter grupper	${\overline {R}}_{3}$ , [4,4,3]
Egenskaper	Vertex-transitiv

Den kantellerade, fyrkantiga bikakan , rr{4,4,3}, har cuboctahedron , fyrkantig kakel och triangulära prismafasetter, med en likbent triangulär prisma vertexfigur .

Cantitruncated fyrkantigt kakel bikaka

Cantitruncated fyrkantigt kakel bikaka
Typ	Paracompact enhetlig honeycomb
Schläfli symboler	tr{4,4,3} eller t 0,1,2 {4,4,3}
Coxeter diagram
Celler	t{4,3} tr{4,4} {}x{3}
Ansikten	triangel {3} kvadratisk {4} oktagon {8}
Vertex figur	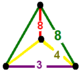likbent triangulär pyramid
Coxeter grupper	${\overline {R}}_{3}$ , [4,4,3]
Egenskaper	Vertex-transitiv

Den utkragade fyrkantiga bikakan , tr{4,4,3}, har avkortad kub , trunkerad kvadratisk plattsättning och triangulära prismafasetter, med en likbent triangulär pyramidformad vertexfigur .

Runcinated fyrkantigt kakel bikaka

Runcinated fyrkantigt kakel bikaka
Typ	Paracompact enhetlig honeycomb
Schläfli symbol	t 0,3 {4,4,3}
Coxeter diagram	↔
Celler	{3,4} {4,4} {}x{4} {}x{3}
Ansikten	triangel {3} kvadrat {4}
Vertex figur	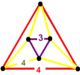oregelbunden triangulär antiprisma
Coxeter grupper	${\overline {R}}_{3}$ , [4,4,3]
Egenskaper	Vertex-transitiv

Den runcinerade fyrkantiga bikakan , t _0,3 {4,4,3}, har oktaeder , triangulärt prisma , kub och fyrkantiga kakelfacetter, med en oregelbunden triangulär antiprisma vertexfigur .

Runcruncated fyrkantigt kakel bikaka

Runcruncated fyrkantigt kakel bikaka
Typ	Paracompact enhetlig honeycomb
Schläfli symboler	t 0,1,3 {4,4,3} s 2,3 {3,4,4}
Coxeter diagram
Celler	rr{4,3} t{4,4} {}x{3} {}x{8}
Ansikten	triangel {3} kvadratisk {4} oktagon {8}
Vertex figur	likbent-trapesformad pyramid
Coxeter grupper	${\overline {R}}_{3}$ , [4,4,3]
Egenskaper	Vertex-transitiv

Den runda, fyrkantiga bikakan , t _0,1,3 {4,4,3}, har rhombicuboctahedron , åttkantiga prisma , triangulära prisma och trunkerade fyrkantiga kakelfasetter, med en likbent trapetsformad pyramidformad vertexfigur .

Runcikantellerad bikaka med fyrkantigt kakel

Den runcikantellerade fyrkantiga bikakan är samma som den runcikanterade ordnings-4 oktaedriska bikakan .

Omnitruncated fyrkantigt kakel bikaka

Omnitruncated fyrkantigt kakel bikaka
Typ	Paracompact enhetlig honeycomb
Schläfli symbol	t 0,1,2,3 {4,4,3}
Coxeter diagram
Celler	tr{4,4} {}x{6} {}x{8} tr{4,3}
Ansikten	kvadratisk {4} sexkant {6} oktagon {8}
Vertex figur	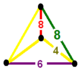oregelbunden tetraeder
Coxeter grupper	${\overline {R}}_{3}$ , [4,4,3]
Egenskaper	Vertex-transitiv

Den omnitruncerade fyrkantiga bikakan , t _0,1,2,3 {4,4,3}, har trunkerad kvadratisk plattsättning , trunkerad cuboctahedron , hexagonal prisma och åttkantiga prismafacetter, med en oregelbunden tetrahedron vertexfigur .

Omnisnub fyrkantigt kakelkaka

Omnisnub fyrkantigt kakelkaka
Typ	Paracompact enhetlig honeycomb
Schläfli symbol	h(t 0,1,2,3 {4,4,3})
Coxeter diagram
Celler	sr{4,4} sr{2,3} sr{2,4} sr{4,3}
Ansikten	triangel {3} kvadrat {4}
Vertex figur	oregelbunden tetraeder
Coxeter grupp	[4,4,3] +
Egenskaper	Olikformig, vertextransitiv

Den alternerade omnitrunkerade fyrkantiga bikakan (eller omnisnub kvadratisk tegel honeycomb ), h ( t _0,1,2,3 {4,4,3}), har snub kvadratisk plattsättning , snub kub , triangulär antiprisma , kvadrat antiprisma och tetraederceller , med en oregelbunden tetrahedron vertex figur .

Alternativt fyrkantigt kakel bikaka

Alternativt fyrkantigt kakel bikaka
Typ	Paracompact uniform honeycomb Halvregelbunden honeycomb
Schläfli symbol	h{4,4,3} tim{4,4,4} {(4,3,3,4)} h{4 1,1,1 }
Coxeter diagram	↔ ↔ ↔ ↔ ↔ ↔
Celler	{4,4} {4,3}
Ansikten	kvadrat {4}
Vertex figur	kuboktaeder
Coxeter grupper	${\overline {O}}_{3}$ , [3,4 1,1 ] [4,1 + ,4,4] ↔ [∞,4,4,∞] ${\widehat {BR}}_{3}$ , [(4,4,3,3)] [1 + ,4 1,1,1 ] ↔ [∞ [6] ]
Egenskaper	Vertextransitiv, kanttransitiv, kvasiregelbunden

Den alternerade fyrkantiga bikakan , h{4,4,3}, är en kvasiregelbunden parakompakt enhetlig bikaka i hyperboliskt 3-rum. Den har kub- och fyrkantiga kakelfacetter i en cuboctahedron vertexfigur.

Cantic fyrkantigt kakel honungskaka

Cantic fyrkantigt kakel honungskaka
Typ	Paracompact enhetlig honeycomb
Schläfli symbol	h 2 {4,4,3}
Coxeter diagram	↔
Celler	t{4,4} r{4,3} t{4,3}
Ansikten	triangel {3} kvadratisk {4} oktagon {8}
Vertex figur	rektangulär pyramid
Coxeter grupper	${\overline {O}}_{3}$ , [3,4 1,1 ]
Egenskaper	Vertex-transitiv

Den kantiska fyrkantiga honeycomb , h ₂ {4,4,3}, är en parakompakt enhetlig honeycomb i hyperboliskt 3-utrymme. Den har avkortat kvadrerar kakel , avkortat kub , och cuboctahedron facetter, med en rektangulär pyramid vertex figur .

Runcic fyrkantigt kakel honungskaka

Runcic fyrkantigt kakel honungskaka
Typ	Paracompact enhetlig honeycomb
Schläfli symbol	h 3 {4,4,3}
Coxeter diagram	↔
Celler	{4,4} r{4,3} {3,4}
Ansikten	triangel {3} kvadrat {4}
Vertex figur	kvadratisk frustum
Coxeter grupper	${\overline {O}}_{3}$ , [3,4 1,1 ]
Egenskaper	Vertex-transitiv

Den runkiska fyrkantiga honeycomb , h ₃ {4,4,3}, är en parakompakt enhetlig honeycomb i hyperboliskt 3-utrymme. Den har fyrkantiga kakel , rhombicuboctahedron och oktaederfacetter i en fyrkantig frustum vertexfigur.

Runcicantic fyrkantigt kakel bikaka

Runcicantic fyrkantigt kakel bikaka
Typ	Paracompact enhetlig honeycomb
Schläfli symbol	h 2,3 {4,4,3}
Coxeter diagram	↔
Celler	t{4,4} tr{4,3} t{3,4}
Ansikten	kvadratisk {4} sexkant {6} oktagon {8}
Vertex figur	spegelvänd sphenoid
Coxeter grupper	${\overline {O}}_{3}$ , [3,4 1,1 ]
Egenskaper	Vertex-transitiv

Den runcicantiska fyrkantiga bikakan , h _2,3 {4,4,3}, ↔ , är en parakompakt enhetlig bikaka i hyperboliskt 3-rum. Den har trunkerade kvadratiska plattor , trunkerade cuboctahedron och trunkerade oktaederfasetter i en spegelvänd sphenoid vertexfigur .

Alternerad rätad fyrkantig kakel bikaka

Alternerad rätad fyrkantig kakel bikaka
Typ	Paracompact enhetlig honeycomb
Schläfli symbol	hr{4,4,3}
Coxeter diagram	↔
Celler
ansikten
Vertex figur	trekantsprisma
Coxeter grupper	[4,1 + ,4,3] = [∞,3,3,∞]
Egenskaper	Osimplektisk, vertextransitiv

Den alternerade, rektifierade, fyrkantiga bikakan är en parakompakt enhetlig bikaka i hyperboliskt 3-utrymme.

Se även

• Konvexa enhetliga bikakor i hyperboliskt utrymme
• Regelbundna tesselleringar av hyperboliskt 3-mellanslag
• Paracompact enhetliga honungskakor

•   Coxeter , Regular Polytopes , 3:a. ed., Dover Publications, 1973. ISBN 0-486-61480-8 . (Tabell I och II: Vanliga polytoper och honeycombs, s. 294–296)
•     The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN 99-35678 , ISBN 0-486-40919-8 (Kapitel 10, Regular Honeycombs in Hyperbolic Space ) Tabell III
•   Jeffrey R. Weeks The Shape of Space, 2:a upplagan ISBN 0-8247-0709-5 (Kapitel 16-17: Geometries on Three-manifolds I,II)
• Norman Johnson Uniform Polytopes , Manuskript
  • NW Johnson : Theory of Uniform Polytopes and Honeycombs , Ph.D. Avhandling, University of Toronto, 1966
  • NW Johnson: Geometries and Transformations , (2018) Kapitel 13: Hyperboliska Coxeter-grupper
  • Norman W. Johnson och Asia Ivic Weiss Quadratic Heltal och Coxeter Groups PDF Can. J. Math. Vol. 51 (6), 1999 s. 1307–1336