Triangulär kakel

Triangulär kakel

Typ	Vanlig kakelsättning
Vertex-konfiguration	3.3.3.3.3.3 (eller 3 ⁶ )
Ansiktskonfiguration	V6.6.6 (eller V6 ³ )
Schläfli symbol(er)	{3,6} {3 ^[3] }
Wythoff symbol(er)	6 \| 3 2 3 \| 3 3 \| 3 3 3
Coxeter-diagram(n)	=
Symmetri	p6m , [6,3], (*632)
Rotationssymmetri	p6 , [6,3] ⁺ , (632) p3 , [3 ^[3] ] ⁺ , (333)
Dubbel	Sexkantigt kakel
Egenskaper	Vertextransitiv , kanttransitiv , ansiktstransitiv

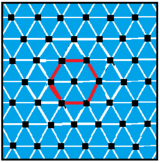
Inom geometrin är den triangulära plattsättningen eller triangulära tessellationen en av de tre regelbundna plattorna på det euklidiska planet , och är den enda sådan plattsättning där de ingående formerna inte är parallellogoner . Eftersom den liksidiga triangelns inre vinkel är 60 grader, upptar sex trianglar vid en punkt hela 360 grader. Den triangulära plattan har Schläfli-symbolen { $3,6}.$

Den engelske matematikern John Conway kallade det en deltille , uppkallad från den triangulära formen av den grekiska bokstaven delta (Δ). Den triangulära plattsättningen kan också kallas en kishextille genom en kis -operation som lägger till en mittpunkt och trianglar för att ersätta ytorna på en hextille .

Det är en av tre vanliga plattsättningar av planet . De andra två är den fyrkantiga plattsättningen och den sexkantiga plattsättningen .

Enhetliga färger

En 2-uniform triangulär plattsättning, 4 färgade trianglar, relaterad till den geodetiska polyedern som {3,6+} _2,0 .

Det finns 9 distinkta enhetliga färger av en triangulär plattsättning. (Att namnge färgerna med index på de 6 trianglarna runt en vertex: 111111, 111112, 111212, 111213, 111222, 112122, 121212, 121213, 121313, 111112, 111212, 111213. 112 från 121213 av kombinerar 1 och 3, medan 111213 reduceras från 121314.

Det finns en klass av arkimediska färger , 111112, (markerad med en *) som inte är 1-uniform, som innehåller omväxlande rader av trianglar där var tredje är färgad. Exemplet som visas är 2-uniform, men det finns oändligt många sådana arkimediska färger som kan skapas genom godtyckliga horisontella förskjutningar av raderna.

111111	121212	111222	112122	111112 (*)

p6m (*632)	p3m1 (*333)	cmm (2*22)	p2 (2222)	p2 (2222)

121213	111212	111112	121314	111213

p31m (3*3)			p3 (333)

A2 galler- och cirkelpackningar

A
^*₂ gitter som tre triangulära plattor: + +

Spetsarrangemanget för den triangulära plattsättningen kallas ett A ₂ gitter - . Det är det 2-dimensionella fallet av en enkelkisk honungskaka .

A
^*₂ -gittret (även kallat A
³₂ ) kan konstrueras genom föreningen av alla tre A _2- gittret, och ekvivalent med A ₂ -gittret.

+ + = dubbel av =

Topparna på den triangulära plattsättningen är centrum för den tätaste möjliga cirkelpackningen . Varje cirkel är i kontakt med 6 andra cirklar i förpackningen ( kyssnummer) . Packningsdensiteten är $π$ ⁄ √ 12 eller 90,69 %. Voronoi -cellen i en triangulär plattsättning är en hexagon , och så har voronoi-tesselationen , den hexagonala plattsättningen, en direkt överensstämmelse med cirkelpackningarna.

Geometriska variationer

Triangulära plattsättningar kan göras med motsvarande {3,6}-topologi som den vanliga plattsättningen (6 trianglar runt varje vertex). Med identiska ansikten ( ansiktstransitivitet ) och vertextransitivitet finns det 5 varianter. Given symmetri antar att alla ansikten har samma färg.

Skalen triangel p2 symmetri
Skalen triangel pmg symmetri
Likbent triangel cmm symmetri
Rätt triangel cmm symmetri
Liksidig triangel p6m symmetri

Relaterade polyedrar och plattsättningar

De plana plattorna är relaterade till polyedrar . Att sätta färre trianglar på en vertex lämnar en lucka och gör att den kan vikas till en pyramid . Dessa kan utökas till platoniska solider : fem, fyra och tre trianglar på en vertex definierar en icosahedron , oktaeder och tetraeder respektive.

Denna beläggning är topologiskt relaterad som en del av sekvensen av vanliga polyedrar med Schläfli-symboler {3,n}, som fortsätter in i det hyperboliska planet .

* n 32 symmetrimutation av regelbundna plattsättningar: {3, n }
Sfärisk				Euklid.	Kompakt hyper.		Paraco.	Icke-kompakt hyperbolisk

3.3	3 ³	3 ⁴	3 ⁵	3 ⁶	3 ⁷	3 ⁸	3 ^∞	3 ¹²ⁱ	3 ⁹ⁱ	3 ⁶ⁱ	3 ³ⁱ

Det är också topologiskt relaterat som en del av sekvensen av katalanska fasta ämnen med ansiktskonfiguration Vn.6.6, och fortsätter även in i det hyperboliska planet.

V3.6.6	V4.6.6	V5.6.6	V6.6.6	V7.6.6

Wythoff-konstruktioner från sexkantiga och triangulära plattor

Liksom de enhetliga polyedrarna finns det åtta enhetliga plattsättningar som kan baseras på den vanliga hexagonala plattsättningen (eller den dubbla triangulära plattsättningen).

Genom att rita brickorna färgade som röda på originalytorna, gula vid de ursprungliga hörnen och blå längs originalkanterna, finns det 8 former, 7 som är topologiskt distinkta. (Den stympade triangulära plattsättningen är topologiskt identisk med den hexagonala plattsättningen.)

Enhetliga sexkantiga/triangulära plattor
Grundläggande domäner	Symmetri : [6,3], (*632)							[6,3] ⁺ , (632)
	{6,3}	t{6,3}	r{6,3}	t{3,6}	{3,6}	rr{6,3}	tr{6,3}	sr{6,3}


Konfig.	6 ³	3.12.12	(6.3) ²	6.6.6	3 ⁶	3.4.6.4	4.6.12	3.3.3.3.6

Triangulära symmetriplattor
Wythoff	3 \| 3 3	3 3 \| 3	3 \| 3 3	3 3 \| 3	3 \| 3 3	3 3 \| 3	3 3 3 \|	\| 3 3 3
Coxeter
Bild Vertex figur	(3.3) ³	3.6.3.6	(3.3) ³	3.6.3.6	(3.3) ³	3.6.3.6	6.6.6	3.3.3.3.3.3

Besläktade regelbundna komplexa apeirogoner

Det finns 4 vanliga komplexa apeirogoner , som delar hörnen på den triangulära plattsättningen. Regelbundna komplexa apeirogoner har hörn och kanter, där kanter kan innehålla 2 eller fler hörn. Reguljära apeirogoner p { q } r begränsas av: 1/ p + 2/ q + 1/ r = 1. Kanter har p hörn, och vertexfigurer är r -gonala.

Den första är gjord av 2-kanter, och nästa två är triangulära kanter, och den sista har överlappande sexkantiga kanter.

2{6}6 eller	3{4}6 eller	3{6}3 eller	6{3}6 eller

Andra triangulära plattor

Det finns också tre Laves plattsättningar gjorda av enkel typ av trianglar:

Kisrhombille 30°-60°-90° rätvinkliga trianglar	Kisquadrille 45°-45°-90° rätvinkliga trianglar	Kisdeltil 30°-30°-120° likbenta trianglar

Se även

Triangulär kakelkaka
Enkel bikaka
Plattläggning av vanliga polygoner
Lista över enhetliga plattsättningar
Isogrid (strukturell design med triangulär kakel)

Coxeter, HSM Regular Polytopes , (3:e upplagan, 1973), Dover-upplagan, ISBN 0-486-61480-8 sid. 296, Tabell II: Vanliga bikakor
Grünbaum, Branko & Shephard, GC (1987). Kakel och mönster . New York: WH Freeman. ISBN 0-7167-1193-1 . (Kapitel 2.1: Regelbundna och enhetliga plattsättningar , s. 58-65, kapitel 2.9 Arkimedeiska och enhetliga färgsättningar s. 102–107)
Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design . Dover Publications, Inc. ISBN 0-486-23729-X . s35
John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 [1]

externa länkar

Weisstein, Eric W. "Triangular Grid" . MathWorld .
- Weisstein, Eric W. "Regelbunden tessellation" . MathWorld .
- Weisstein, Eric W. "Uniform tessellation" . MathWorld .
Klitzing, Richard. "2D euklidiska plattsättningar x3o6o - trat - O2" .

Fundamentala konvexa regelbundna och enhetliga bikakor i dimensionerna 2–9
Plats	Familj	${\tilde {A}}_{n-1}$	${\tilde {C}}_{n-1}$	${\tilde {B}}_{n-1}$	${\tilde {D}}_{n-1}$	${\tilde {G}}_{2}$ / ${\tilde {F}}_{4}$ / ${\tilde { E}}_{n-1}$
E ²	Enhetlig plattsättning	{3 ^[3] }	δ ₃	hδ ₃	qδ ₃	Hexagonal
E ³	Enhetlig konvex bikaka	{3 ^[4] }	δ ₄	hδ ₄	qδ ₄
E ⁴	Uniform 4-honeycomb	{3 ^[5] }	δ ₅	hδ ₅	qδ ₅	24-cells honungskaka
E ⁵	Uniform 5-bikaka	{3 ^[6] }	δ ₆	hδ ₆	qδ ₆
E ⁶	Uniform 6-honeycomb	{3 ^[7] }	δ ₇	hδ ₇	qδ ₇	2 ₂₂
E ⁷	Uniform 7-honeycomb	{3 ^[8] }	δ ₈	hδ ₈	qδ ₈	1 ₃₃ • 3 ₃₁
E ⁸	Uniform 8-honeycomb	{3 ^[9] }	δ ₉	hδ ₉	qδ ₉	1 ₅₂ • 2 ₅₁ • 5 ₂₁
E ⁹	Uniform 9-honeycomb	{3 ^[10] }	δ ₁₀	hδ ₁₀	qδ ₁₀
E ¹⁰	Uniform 10-honeycomb	{3 ^[11] }	δ ₁₁	hδ ₁₁	qδ ₁₁
E ^{n -1}	Uniform ( n -1)- honeycomb	{3 ^[n] }	5 _n	hδ _n	qδ _n	1 _k2 • 2 _k1 • k ₂₁