Enhetlig plattsättning

Inom geometri är en enhetlig plattsättning en tessellation av planet med regelbundna polygonytor med begränsningen att vara vertex-transitive .

Enhetliga plattsättningar kan förekomma i både det euklidiska planet och det hyperboliska planet . Enhetliga plattsättningar är relaterade till de finita enhetliga polyedrarna som kan anses vara enhetliga plattsättningar av sfären .

De flesta enhetliga plattsättningar kan göras från en Wythoff-konstruktion som börjar med en symmetrigrupp och en singulär generatorpunkt inuti den fundamentala domänen . En plan symmetrigrupp har en polygonal fundamental domän och kan representeras av gruppnamnet som representeras av speglarnas ordning i sekventiella hörn.

En fundamental domäntriangel är ( p q r ), och en rätvinklig triangel ( p q 2), där p , q , r är heltal större än 1. Triangeln kan existera som en sfärisk triangel , en euklidisk plan triangel eller en hyperbolisk plan triangel, beroende på värdena för p , q och r .

Det finns ett antal symboliska scheman för att namnge dessa figurer, från en modifierad Schläfli-symbol för rätvinkliga domäner: ( p q 2) → { p , q }. Coxeter -Dynkin-diagrammet är en triangulär graf med p , q , r märkta på kanterna. Om r = 2 är grafen linjär eftersom domännoder för order-2 inte genererar några reflektioner. Wythoff -symbolen tar de 3 heltal och skiljer dem åt med en vertikal streck (|). Om generatorpunkten är utanför spegeln mittemot en domännod, ges den före stapeln.

Slutligen kan plattsättningar beskrivas av deras vertexkonfiguration , sekvensen av polygoner runt varje vertex.

Alla enhetliga plattsättningar kan konstrueras från olika operationer som appliceras på vanliga plattsättningar . Dessa operationer som nämnts av Norman Johnson kallas trunkering (skärande hörn), korrigering (skärning av hörn tills kanterna försvinner) och cantellation (skärkanter). Omnitrunkering är en operation som kombinerar trunkering och kantellering. Snubbing är en operation med alternativ trunkering av den omnitrunkerade formen. (Se Uniform polyhedron#Wythoff konstruktionsoperatörer för mer information.)

Coxeter grupper

Coxeter-grupper för planet definierar Wythoff-konstruktionen och kan representeras av Coxeter-Dynkin-diagram :

För grupper med heltalsorder, inklusive:

Euklidiskt plan
Orbifold symmetri	Coxeter grupp			anteckningar
Kompakt
*333	(3 3 3)	${\tilde {A}}_{2}$	[3 ^[3] ]	3 reflekterande former, 1 snubb
*442	(4 4 2)	${\tilde {B}}_{2}$	[4,4]	5 reflekterande former, 1 snubb
*632	(6 3 2)	${\tilde {G}}_{2}$	[6,3]	7 reflekterande former, 1 snubb
*2222	(∞ 2 ∞ 2)	${\tilde {I}}_{1}$ × ${\tilde {I}}_{1}$	[∞,2,∞]	3 reflekterande former, 1 snubb
Icke-kompakt ( fris )
*∞∞	(∞)	${\tilde {I}}_{1}$	[∞]
*22∞	(2 2 ∞)	${\tilde {I}}_{1}$ × ${\tilde {A}}_{2}$	[∞,2]	2 reflekterande former, 1 snubb

Hyperboliskt plan
Orbifold symmetri	Coxeter grupp		anteckningar
Kompakt
*pq2	(pq 2)	[p,q]	2(p+q) < pq
*pqr	(pqr)	[(p,q,r)]	pq+pr+qr < pqr
Paracompact
*∞p2	(s ∞ 2)	[p,∞]	p>=3
*∞pq	(pq ∞)	[(p,q,∞)]	p,q>=3, p+q>6
*∞∞s	(p ∞ ∞)	[(p,∞,∞)]	p>=3
*∞∞∞	(∞ ∞ ∞)	[(∞,∞,∞)]

Enhetliga plattsättningar av det euklidiska planet

Den långsträckta triangulära plattsättningen, den enda icke-wythoffiska konvexa enhetliga plattsättningen

Det finns symmetrigrupper på det euklidiska planet konstruerade från fundamentala trianglar: (4 4 2), (6 3 2) och (3 3 3). Var och en representeras av en uppsättning reflektionslinjer som delar upp planet i grundläggande trianglar.

Dessa symmetrigrupper skapar 3 vanliga plattsättningar och 7 halvregelbundna. Ett antal av de halvregelbundna plattorna upprepas från olika symmetrikonstruktörer.

En prismatisk symmetrigrupp representerad av (2 2 2 2) representeras av två uppsättningar parallella speglar, som i allmänhet kan ha en rektangulär fundamental domän. Det genererar inga nya plattor.

Ytterligare en prismatisk symmetrigrupp representerad av (∞ 2 2) som har en oändlig fundamental domän. Den konstruerar två enhetliga plattsättningar, det apeirogonala prismat och det apeirogonala antiprismat .

Staplingen av de ändliga ytorna av dessa två prismatiska plattsättningar konstruerar en icke-wythoffsk enhetlig plattsättning av planet. Det kallas den långsträckta triangulära plattsättningen , som består av omväxlande lager av kvadrater och trianglar.

Rättvinkla grundtrianglar: ( p q 2)

( s q 2)	Fond. trianglar	Förälder	Trunkerad	Rättad till	Bitruncated	Birectified (dubbel)	Kantellerad	Omnitruncated ( Cantitruncated )	Nonchalera
Wythoff symbol		q \| p 2	2 q \| sid	2 \| p q	2 p \| q	p \| q 2	p q \| 2	p q 2 \|	\| p q 2
Schläfli symbol		{ p , q }	t { p , q }	r{p,q}	2t{p,q}=t{q,p}	2r{p,q}={q,p}	rr{p,q}	tr{p,q}	sr{p,q}
Coxeter diagram
Vertex konfiguration.		p ^q	q.2p.2p	(pq) ²	sid. 2q.2q	q ^sid	sid. 4.q.4	4,2p.2q	3.3.p. 3.q
Fyrkantig kakel (4 4 2)	0	{4,4}	4.8.8	4.4.4.4	4.8.8	{4,4}	4.4.4.4	4.8.8	3.3.4.3.4
Hexagonal kakel (6 3 2)	0	{6,3}	3.12.12	3.6.3.6	6.6.6	{3,6}	3.4.6.4	4.6.12	3.3.3.3.6

Allmänna grundtrianglar: (pqr)

Wythoff-symbol (pqr)	Fond. trianglar	q \| pr	rq \| sid	r \| pq	rp \| q	p \| qr	pq \| r	pqr \|	\| pqr
Coxeter diagram
Vertex konfiguration.		(pq) ^r	r.2p.q.2p	(pr) ^q	q.2r.p. 2r	(qr) ^sid	q.2r.p. 2r	r.2q.p. 2q	3.r.3.q.3.p
Triangulär (3 3 3)	0	(3.3) ³	3.6.3.6	(3.3) ³	3.6.3.6	(3.3) ³	3.6.3.6	6.6.6	3.3.3.3.3.3

Icke-enkla fundamentala domäner

Den enda möjliga fundamentala domänen i euklidiskt 2-rum som inte är en simplex är rektangeln (∞ 2 ∞ 2), med Coxeter-diagram : . Alla former som genereras av den blir en kvadratisk plattsättning .

Enhetliga plattsättningar av det hyperboliska planet

Det finns oändligt många enhetliga plattsättningar av konvexa regelbundna polygoner på det hyperboliska planet , var och en baserad på en annan reflekterande symmetrigrupp (pqr).

Ett prov visas här med en Poincaré-skivprojektion .

Coxeter -Dynkin-diagrammet ges i linjär form, även om det faktiskt är en triangel, med det efterföljande segmentet r som ansluter till den första noden.

Ytterligare symmetrigrupper finns i det hyperboliska planet med fyrsidiga fundamentala domäner som börjar med (2 2 2 3), etc., som kan generera nya former. Det finns också grundläggande domäner som placerar hörn i oändligheten, såsom (∞ 2 3), etc.

Rättvinkla grundtrianglar: ( p q 2)

(pq 2)	Fond. trianglar	Förälder	Trunkerad	Rättad till	Bitruncated	Birectified (dubbel)	Kantellerad	Omnitruncated ( Cantitruncated )	Nonchalera
Wythoff symbol		q \| p 2	2 q \| sid	2 \| pq	2 p \| q	p \| q 2	pq \| 2	pq 2 \|	\| pq 2
Schläfli symbol		t{p,q}	t{p,q}	r{p,q}	2t{p,q}=t{q,p}	2r{p,q}={q,p}	rr{p,q}	tr{p,q}	sr{p,q}
Coxeter diagram
Vertex figur		p ^q	(q.2p.2p)	(pqpq)	(sid. 2q.2q)	q ^sid	(sid. 4.q.4)	(4.2p.2q)	(3.3.s. 3.q)
(5 4 2)	V4.8.10	{5,4}	4.10.10	4.5.4.5	5.8.8	{4,5}	4.4.5.4	4.8.10	3.3.4.3.5
(5 5 2)	V4.10.10	{5,5}	5.10.10	5.5.5.5	5.10.10	{5,5}	5.4.5.4	4.10.10	3.3.5.3.5
(7 3 2)	V4.6.14	{7,3}	3.14.14	3.7.3.7	7.6.6	{3,7}	3.4.7.4	4.6.14	3.3.3.3.7
(8 3 2)	V4.6.16	{8,3}	3.16.16	3.8.3.8	8.6.6	{3,8}	3.4.8.4	4.6.16	3.3.3.3.8

Allmänna grundtrianglar (pqr)

Wythoff-symbol (pqr)	Fond. trianglar	q \| pr	rq \| sid	r \| pq	rp \| q	p \| qr	pq \| r	pqr \|	\| pqr
Coxeter diagram
Vertex figur		(pr) ^q	(r.2p.q.2p)	(pq) ^r	(q.2r.p. 2r)	(qr) ^sid	(r.2q.p. 2q)	(2p.2q.2r)	(3.r.3.q.3.p)
(4 3 3)	V6.6.8	(3.4) ³	3.8.3.8	(3.4) ³	3.6.4.6	(3.3) ⁴	3.6.4.6	6.6.8	3.3.3.3.3.4
(4 4 3)	V6.8.8	(3.4) ⁴	3.8.4.8	(4.4) ³	3.6.4.6	(3.4) ⁴	4.6.4.6	6.8.8	3.3.3.4.3.4
(4 4 4)	V8.8.8	(4.4) ⁴	4.8.4.8	(4.4) ⁴	4.8.4.8	(4.4) ⁴	4.8.4.8	8.8.8	3.4.3.4.3.4

Utökade listor över enhetliga plattsättningar

Hönsfigurerna för de sex plattorna med konvexa regelbundna polygoner och apeirogonytor . ( Wythoff - symbolen anges i rött.)

Vertexfigurer för 21 enhetliga plattsättningar.

Det finns ett antal sätt listan över enhetliga plattsättningar kan utökas på:

Vertexfigurer kan ha retrograda ansikten och vända sig runt vertexen mer än en gång.
Stjärnpolygonbrickor kan inkluderas.
Apeirogoner , {∞}, kan användas som plattsättningsytor.
Sicksackar (apeirogoner som växlar mellan två vinklar) kan också användas.
Begränsningen att plattor möts kant till kant kan lättas upp, vilket tillåter ytterligare plattsättning som pythagoras kakel .

Symmetrigrupptrianglar med retrograder inkluderar:

(4/3 4/3 2) (6 3/2 2) (6/5 3 2) (6 6/5 3) (6 6 3/2)

Symmetrigrupptrianglar med oändlighet inkluderar:

(4 4/3 ∞) (3/2 3 ∞) (6 6/5 ∞) (3 3/2 ∞)

Branko Grünbaum och GC Shephard , i 1987 års bok Tilings and patterns , räknar i avsnitt 12.3 upp en lista med 25 enhetliga plattsättningar, inklusive de 11 konvexa formerna, och lägger till 14 till som de kallar ihåliga plattsättningar som inkluderade de två första expansionerna ovan, stjärnpolygonytor och vertexfigurer.

HSM Coxeter , MS Longuet-Higgins och JCP Miller , i 1954 års tidning 'Uniform polyhedra', i Tabell 8: Uniform Tessellations, använder de tre första expansionerna och räknar upp totalt 38 enhetliga plattsättningar. Om en plattsättning gjord av 2 apeirogoner också räknas kan summan anses vara 39 enhetliga plattsättningar.

listade Grünbaum, Miller och Shephard i sin tidning Uniform Tilings with Hollow Tiles 25 plattsättningar med de två första expansionerna och 28 fler när den tredje läggs till (vilket gör 53 enligt Coxeter et al.s definition). När den fjärde läggs till listar de ytterligare 23 enhetliga plattsättningar och 10 familjer (8 beroende på kontinuerliga parametrar och 2 på diskreta parametrar).

Förutom de 11 konvexa lösningarna, de 28 enhetliga stjärnplattorna listade av Coxeter et al. , grupperade efter delade kantgrafer, visas nedan, följt av ytterligare 15 listade av Grünbaum et al. som uppfyller Coxeter et al.s definition men som saknades av dem.

Denna uppsättning har inte bevisats vara komplett. Med "2,25" menas plattsättning 25 i Grünbaum et al:s tabell 2 från 1981.

Följande tre plattsättningar är exceptionella genom att det bara finns ändligt många av en ansiktstyp: två apeirogoner i varje. Ibland ingår inte order-2 apeirogonal plattsättning, eftersom dess två ytor möts vid mer än en kant.

Frisgruppsymmetri _
McNeill	Vertex Config	Wythoff	Symmetri	Anteckningar
I1	∞.∞		p1m1	(Två halvplansplattor, order-2 apeirogonala plattor )
I2	4.4.∞	∞ 2 \| 2	p1m1	Apeirogonalt prisma
I3	3.3.3.∞	\| 2 2 ∞	sid 11g	Apeirogonal antiprisma

För tydlighetens skull är apeirogoner inte färgade härifrån och framåt. En uppsättning polygoner runt en vertex är markerad. McNeill listar endast plattsättningar som ges av Coxeter et al. (1954). De elva konvexa enhetliga plattorna har upprepats som referens.

Tapetgruppsymmetri _
McNeill	Grünbaum et al 1981	Kantdiagram _	Markerad	Vertex Config	Wythoff	Symmetri
Konvex	1.9			4.4.4.4	4 \| 2 4	p4m
I4	2.14			4.∞.4/3.∞ 4.∞.-4.∞	4/3 4 \| ∞	p4m
Konvex	1.24			6.6.6	3 \| 2 6	p6m
Konvex	1,25			3.3.3.3.3.3	6 \| 2 3	p6m
I5	2.26			(3.∞.3.∞.3.∞)/2	3/2 \| 3 ∞	p3m1
Konvex	1.23			3.6.3.6	2 \| 3 6	p6m
I6	2,25			6.∞.6/5.∞ 6.∞.-6.∞	6/5 6 \| ∞	p6m
I7	2.24			∞.3.∞.3/2 3.∞.-3.∞	3/2 3 \| ∞	p6m
Konvex	1.14			3.4.6.4	3 6 \| 2	p6m
1	1.15			3/2.12.6.12 -3.12.6.12	3/2 6 \| 6	p6m
1	1.16			4.12.4/3.12/11 4.12.-4.-12	2 6 (3/2 6/2) \|	p6m
Konvex	1.5			4.8.8	2 4 \| 4	p4m
2	2.7			4,8/3.∞.8/3	4 ∞ \| 4/3	p4m
	1.7			8/3.8.8/5.8/7 8.8/3.-8.-8/3	4/3 4 (4/2 ∞/2) \|	p4m
	2.6			8.4/3.8.∞ -4.8.∞.8	4/3 ∞ \| 4	p4m
Konvex	1.20			3.12.12	2 3 \| 6	p6m
3	2.17			6.12/5.∞.12/5	6 ∞ \| 6/5	p6m
	1.21			12/5.12.12/7.12/11 12.12/5.-12.-12/5	6/5 6 (6/2 ∞/2) \|	p6m
	2.16			12.6/5.12.∞ -6.12.∞.12	6/5 ∞ \| 6	p6m
4	1.18		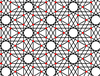	12/5.3.12/5.6/5 3.12/5.-6.12/5	3 6 \| 6/5	p6m
	1.19			12/5.4.12/7.4/3 4.12/5.-4.-12/5	2 6/5 (3/2 6/2) \|	p6m
	1.17			4.3/2.4.6/5 3.-4.6.-4	3/2 6 \| 2	p6m
5	2.5			8.8/3.∞	4/3 4 ∞ \|	p4m
6	2.15			12.12/5.∞	6/5 6 ∞ \|	p6m
7	1.6		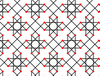	8,4/3,8/5 4,-8,8/3	2 4/3 4 \|	p4m
Konvex	1.11			4.6.12	2 3 6 \|	p6m
8	1.13		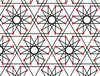	6.4/3.12/7 4.-6.12/5	2 3 6/5 \|	p6m
9	1.12			12.6/5.12/7 6.-12.12/5	3 6/5 6 \|	p6m
10	1.8		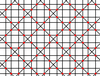	4,8/5,8/5 -4,8/3,8/3	2 4 \| 4/3	p4m
11	1.22		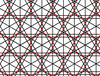	12/5.12/5.3/2 -3.12/5.12/5	2 3 \| 6/5	p6m
Konvex	1.1			3.3.3.4.4	icke-Wythoffian	cmm
12	1.2			4.4.3/2.3/2.3/2 3.3.3.-4.-4	icke-Wythoffian	cmm
Konvex	1.3			3.3.4.3.4	\| 2 4 4	p4g
13	1.4			4.3/2.4.3/2.3/2 3.3.-4.3.-4	\| 2 4/3 4/3	p4g
14	2.4			3.4.3.4/3.3.∞ 3.4.3.-4.3.∞	\| 4/3 4 ∞	p4
Konvex	1.10			3.3.3.3.6	\| 2 3 6	s6
	2.1			3/2.∞.3/2.∞.3/2.4/3.4/3 3.4.4.3.∞.3.∞	icke-Wythoffian	cmm
	2.2			3/2.∞.3/2.∞.3/2.4.4 3.-4.-4.3.∞.3.∞	icke-Wythoffian	cmm
	2.3			3/2.∞.3/2.4.4.3/2.4/3.4/3 3.4.4.3.-4.-4.3.∞	icke-Wythoffian	p3
	2.8			4.∞.4/3.8/3.8 4.8.8/3.-4.∞	icke-Wythoffian	p4m
	2.9			4.∞.4.8.8/3 -4.8.8/3.4.∞	icke-Wythoffian	p4m
	2.10			4.∞.4/3.8.4/3.8 4.8.-4.8.-4.∞	icke-Wythoffian	p4m
	2.11			4.∞.4/3.8.4/3.8 4.8.-4.8.-4.∞	icke-Wythoffian	p4g
	2.12			4.∞.4/3.8/3.4.8/3 4.8/3.4.8/3.-4.∞	icke-Wythoffian	p4m
	2.13			4.∞.4/3.8/3.4.8/3 4.8/3.4.8/3.-4.∞	icke-Wythoffian	p4g
	2.18			3/2.∞.3/2.4/3.4/3.3/2.4/3.4/3 3.4.4.3.4.4.3.∞	icke-Wythoffian	p6m
	2.19			3/2.∞.3/2.4.4.3/2.4.4 3.-4.-4.3.-4.-4.3.∞	icke-Wythoffian	p6m
	2.20			3/2.∞.3/2.∞.3/2.12/11.6.12/11 3.12.-6.12.3.∞.3.∞	icke-Wythoffian	p6m
	2.21			3/2.∞.3/2.∞.3/2.12.6/5.12 3.-12.6.-12.3.∞.3.∞	icke-Wythoffian	p6m
	2.22			3/2.∞.3/2.∞.3/2.12/7.6/5.12/7 3.12/5.6.12/5.3.∞.3.∞	icke-Wythoffian	p6m
	2.23			3/2.∞.3/2.∞.3/2.12/5.6.12/5 3.-12/5.-6.-12/5.3.∞.3.∞	icke-Wythoffian	p6m

Det finns två enhetliga plattsättningar för vertexfiguren 4.8.-4.8.-4.∞ (Grünbaum et al. 2.10 och 2.11) och även två enhetliga plattsättningar för vertexfiguren 4.8/3.4.8/3.-4.∞ (Grünbaum et al. 2.12 och 2.13), med olika symmetrier. Det finns också en tredje plattsättning för varje vertexfigur som bara är pseudo-uniform (hörn kommer i två symmetribanor). De använder olika uppsättningar av fyrkantiga ansikten. För stjärneuklidiska plattsättningar bestämmer därför inte vertexfiguren nödvändigtvis plattsättningen.

På bilderna nedan är de medföljande rutorna med horisontella och vertikala kanter markerade med en mittpunkt. En enskild ruta har kanter markerade.

2,10 och 2,12 (p4m)
2.11 och 2.13 (p4g)
Pseudo-uniform

Plattorna med sicksack listas nedan. Notationen {∞ ^α } betecknar en sicksack med vinkeln 0 < α < π. Apeirogonen kan betraktas som specialfallet α = π. Symmetrierna anges för det generiska fallet: det finns ibland speciella värden på α som ökar symmetrin. Plattsättningar 3.1 och 3.12 kan till och med bli regelbundna; 3.32 finns redan (den har inga lediga parametrar). Ibland finns det speciella värden på α som gör att plattsättningen degenererar.

Kakelplattor med sicksack
Grünbaum et al 1981	Diagram	Vertex Config	Symmetri
3.1		∞ ^α .∞ ^β .∞ ^γ α+β+γ=2π	p2
3.2		∞ ^α .∞ ^β .-∞ ^α+β 0<α+β≤π	p2
3.3		3.3.∞ ^π-α .-3.∞ ^α+2π/3 0≤α≤π/6	pgg
3.4		3.3.-∞ ^π-α .-3.∞ ^−α+2π/3 0≤α<π/3	pgg
3.5		4.4.∞ ^φ .4.4.-∞ ^φ φ=2 arctan(n/k), nk jämn, (n,k)=1 ritad för φ=2 arctan 2	pmg
3.6		4.4.∞ ^φ .-4.-4.∞ ^φ φ=2 arctan(n/k), nk jämn, (n,k)=1 ritad för φ=2 arctan 1/2	pmg
3.7		3.4.4.3.-∞ ^2π/3 .-3.-∞ ^2π/3	cmm
3.8		3.-4.-4.3.-∞ ^2π/3 .-3.-∞ ^2π/3	cmm
3.9		4.4.∞ ^π/3 .∞.-∞ ^π/3	p2
3.10		4.4.∞ ^2π/3 .∞.-∞ ^2π/3	p2
3.11		∞.∞ ^α .∞.∞ ^−α 0<α<π	cmm
3.12		∞ ^α .∞ ^π-α .∞ ^α .∞ ^π-α 0<α≤π/2	cmm
3.13		3.∞ ^α .-3.-∞ ^α π/3<α<π	p31m
3.14		4.4.∞ ^2π/3 .4.4.-∞ ^2π/3	p31m
3.15		4.4.∞ ^π/3 .-4.-4.-∞ ^π/3	p31m
3.16		4.∞ ^α .-4.-∞ ^α 0<α<π, α≠π/2	p4g
3.17		4.-8.∞ ^π/2 .∞.-∞ ^π/2 .-8	cmm
3.18		4.-8.∞ ^π/2 .∞.-∞ ^π/2 .-8	p4
3.19		4.8/3.∞ ^π/2 .∞.-∞ ^π/2 .8/3	cmm
3,20		4.8/3.∞ ^π/2 .∞.-∞ ^π/2 .8/3	p4
3.21		6.-12.∞ ^π/3 .∞.-∞ ^π/3 .-12	s6
3.22		6.-12.∞ ^2π/3 .∞.-∞ ^2π/3 .-12	s6
3.23		6.12/5.∞ ^π/3 .∞.-∞ ^π/3 .12/5	s6
3.24		6.12/5.∞ ^2π/3 .∞.-∞ ^2π/3 .12/5	s6
3,25		3.3.3.∞ ^2π/3 .-3.∞ ^2π/3	p31m
3,26		3.∞.3.-∞ ^2π/3 .-3.-∞ ^2π/3	centimeter
3.27		3.∞.-∞ ^2π/3 .∞.-∞ ^2π/3 .∞	p31m
3,28		3.∞ ^2π/3 .∞ ^2π/3 .-3.-∞ ^2π/3 .-∞ ^2π/3	p31m
3,29		∞.∞ ^π/3 .∞ ^π/3 .∞.-∞ ^π/3 .-∞ ^π/3	cmm
3.30		∞.∞ ^π/3 .-∞ ^2π/3 .∞.∞ ^2π/3 .-∞ ^π/3	p2
3,31		∞.∞ ^2π/3 .∞ ^2π/3 .∞.-∞ ^2π/3 .-∞ ^2π/3	cmm
3,32		∞ ^π/3 .∞ ^π/³ .∞ ^π/3 .∞ ^{π/3 .∞ π/3} .∞ π ^/3	p6m
3,33		∞ ^π/3 .-∞ ^2π/3 .-∞ ^2π/3 .∞ ^π/3 .-∞ ^2π/3 .-∞ ^2π/3	cmm

Kakelparen 3.17 och 3.18, samt 3.19 och 3.20, har identiska vertexkonfigurationer men olika symmetrier.

Plattor 3.7 till 3.10 har samma kantarrangemang som 2.1 och 2.2; 3.17 till 3.20 har samma kantarrangemang som 2.10 till 2.13; 3.21 till 3.24 har samma kantarrangemang som 2.18 till 2.23; och 3.25 till 3.33 har samma kantarrangemang som 1.25 (den vanliga triangulära plattsättningen).

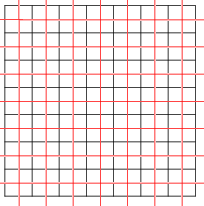
Självdubbla plattsättningar

The {4,4} square tiling (black) with its dual (red).

Plattläggning kan också vara självdubbel . Den fyrkantiga plattsättningen, med Schläfli-symbolen {4,4}, är självdubbel; Här visas två fyrkantiga plattor (röda och svarta), dubbla i förhållande till varandra.

Enhetliga plattsättningar med stjärnpolygoner

Detta exempel, 4,8
^*_π/8 ,4
^**_{π/4 ,} 8
^*_π/4 anses inte kant-till-kant på grund av den stora kvadraten, även om det kan tolkas som stjärnpolygon med par av kolineära kanter.

Att se en stjärnpolygon som en icke-konvex polygon med dubbelt så många sidor tillåter stjärnpolygoner, och om man räknar dessa som vanliga polygoner kan de användas i en enhetlig plattsättning . Dessa polygoner är märkta som {N _α } för en isotoxal icke-konvex 2N-gon med extern dihedrisk vinkel α. Dess yttre hörn är märkta som N
^*_α , och inre N
^**_α . Denna expansion till definitionen kräver hörn med endast 2 polygoner för att inte betraktas som hörn. Plattläggningen definieras av dess vertexkonfiguration som en cyklisk sekvens av konvexa och icke-konvexa polygoner runt varje vertex. Det finns 4 sådana enhetliga plattsättningar med justerbara vinklar α, och 18 enhetliga plattsättningar som bara fungerar med specifika vinklar; ger totalt 22 enhetliga plattsättningar som använder stjärnpolygoner.

Alla dessa plattsättningar är topologiskt relaterade till de vanliga enhetliga plattsättningarna med konvexa regelbundna polygoner, med 2-valens hörn ignorerade och kvadratiska ytor som digoner, reducerade till en enda kant.

4 enhetliga plattsättningar med stjärnpolygoner, vinkel α
3.6 ^_a .6 ^*_a Topologisk 3.12.12	4.4 ^_α .4 ^*_α Topologisk 4.8.8	6.3 ^_a .3 ^*_a Topologisk 6.6.6	3.3 ^_a .3.3 ^*_a Topologisk 3.6.3.6

18 enhetliga plattsättningar med stjärnpolygoner
4.6.4 ^*_π/6 .6 Topologisk 4.4.4.4	(8.4 ^*_π/4 ) ² Topologisk 4.4.4.4	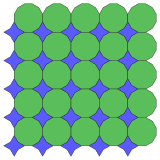12.12.4 ^*_π/3 Topologisk 4.8.8	3.3.8 ^_π/12 .4 ^_π/3 .8 ^_π/12 Topologisk 4.8.8	3.3.8 ^_π/12 .3.4.3.8 ^_π/12 Topologisk 4.8.8	3.4.8.3.8 ^*_π/12 Topologisk 4.8.8
5.5.4 ^_4π/10 .5.4 ^_π/10 Topologisk 3.3.4.3.4	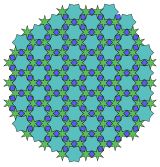4.6 ^_π/6 .6 ^_π/2 .6 ^_π/6 Topologisk 6.6.6	(4,6 ^*_π/6 ) ³ Topologisk 6.6.6	9.9.6 ^*_4π/9 Topologisk 6.6.6	(6,6 ^*_π/3 ) ² Topologisk 3.6.3.6	(12,3 ^*_π/6 ) ² Topologisk 3.6.3.6
3.4.6.3.12 ^*_π/6 Topologisk 4.6.12	3.3.3.12 ^_π/6 .3.3.12 ^_π/6 Topologisk 3.12.12	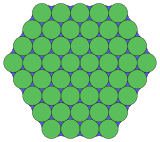18.18.3 ^*_2π/9 Topologisk 3.12.12	3.6.6 ^*_π/3 .6 Topologisk 3.4.6.4	8.3 ^_π/12 .8.6 ^_5π/12 Topologiska 3.4.6.4	9.3.9.3 ^*_π/9 Topologisk 3.6.3.6

Enhetliga plattsättningar med alternerande polygoner

Stjärnpolygoner av formen {p _α } kan också representera konvexa 2 p -goner som alternerar två vinklar, den enklaste är en romb {2 _α }. Genom att tillåta dessa som vanliga polygoner skapas mer enhetliga plattsättningar, med några exempel nedan.

Exempel
3.2.6.2* Topologisk 3.4.6.4	4.4.4.4 Topologisk 4.4.4.4	(2 ^_π/6 .2 ^*_π/3 ) ² Topologisk 4.4.4.4	2 ^_π/6 .2 ^_π/6 .2 ^_π/3 .2 ^_π/3 Topologisk 4.4.4.4	4.2 ^_π/6 .4.2 ^*_π/3 Topologisk 4.4.4.4

Se även

Norman Johnson Uniform Polytopes , Manuscript (1991)
- NW Johnson : Theory of Uniform Polytopes and Honeycombs , Ph.D. Avhandling, University of Toronto, 1966
Grünbaum, Branko ; Shephard, GC (1987). Kakel och mönster . WH Freeman och Company. ISBN 0-7167-1193-1 . (Stjärnplattor avsnitt 12.3)
HSM Coxeter , MS Longuet-Higgins , JCP Miller , Uniform polyhedra , Phil. Trans. 1954, 246 A, 401–50 JSTOR 91532 (Tabell 8)

externa länkar

Grundläggande konvexa regelbundna och enhetliga bikakor i dimensionerna 2–9
Plats	Familj	${\tilde {A}}_{n-1}$	${\tilde {C}}_{n-1}$	${\tilde {B}}_{n-1}$	${\tilde {D}}_{n-1}$	${\tilde {G}}_{2}$ / ${\tilde {F}}_{4}$ / ${\tilde { E}}_{n-1}$
E ²	Enhetlig plattsättning	{3 ^[3] }	δ ₃	hδ ₃	qδ ₃	Hexagonal
E ³	Enhetlig konvex bikaka	{3 ^[4] }	δ ₄	hδ ₄	qδ ₄
E ⁴	Uniform 4-honeycomb	{3 ^[5] }	δ ₅	hδ ₅	qδ ₅	24-cells honungskaka
E ⁵	Uniform 5-bikaka	{3 ^[6] }	δ ₆	hδ ₆	qδ ₆
E ⁶	Uniform 6-honeycomb	{3 ^[7] }	δ ₇	hδ ₇	qδ ₇	2 ₂₂
E ⁷	Uniform 7-honeycomb	{3 ^[8] }	δ ₈	hδ ₈	qδ ₈	1 ₃₃ • 3 ₃₁
E ⁸	Uniform 8-honeycomb	{3 ^[9] }	δ ₉	hδ ₉	qδ ₉	1 ₅₂ • 2 ₅₁ • 5 ₂₁
E ⁹	Uniform 9-honeycomb	{3 ^[10] }	δ ₁₀	hδ ₁₀	qδ ₁₀
E ¹⁰	Uniform 10-honeycomb	{3 ^[11] }	δ ₁₁	hδ ₁₁	qδ ₁₁
E ^{n -1}	Uniform ( n -1)- honeycomb	{3 ^[n] }	5 _n	hδ _n	qδ _n	1 _k2 • 2 _k1 • k ₂₁