Uniform 5-polytop
I geometri är en enhetlig 5-polytop en femdimensionell enhetlig polytop . Per definition är en enhetlig 5-polytop vertextransitiv och konstruerad av enhetliga 4- polytopfasetter .
Den kompletta uppsättningen av konvexa enhetliga 5-polytoper har inte fastställts, men många kan göras som Wythoff-konstruktioner från en liten uppsättning symmetrigrupper . Dessa konstruktionsoperationer representeras av permutationerna av ringar i Coxeter-diagrammen .
Upptäcktshistoria
-
Regelbundna polytoper : (konvexa ytor)
- 1852 : Ludwig Schläfli bevisade i sitt manuskript Theorie der vielfachen Kontinuität att det finns exakt 3 vanliga polytoper i 5 eller fler dimensioner .
-
Konvexa halvregelbundna polytoper : (Olika definitioner före Coxeters uniformskategori )
- 1900 : Thorold Gosset räknade upp listan över ickeprismatiska halvregelbundna konvexa polytoper med regelbundna fasetter ( konvexa regelbundna 4-polytoper ) i sin publikation On the Regular and Semi-Regular Dimensions in Space .
-
Konvexa enhetliga polytoper :
- 1940-1988 : Sökandet utökades systematiskt av HSM Coxeter i hans publikation Regular and Semi-Regular Polytopes I, II och III .
- 1966 : Norman W. Johnson avslutade sin doktorsexamen. Avhandling under Coxeter, The Theory of Uniform Polytopes and Honeycombs, University of Toronto
-
Icke-konvexa enhetliga polytoper :
- 1966 : Johnson beskriver två icke-konvexa enhetliga antiprismor i 5-utrymme i sin avhandling.
- 2000-2023 : Jonathan Bowers och andra forskare söker efter andra icke-konvexa enhetliga 5-polytoper, med ett nuvarande antal av 1297 kända enhetliga 5-polytoper utanför oändliga familjer (konvexa och icke-konvexa), exklusive prismorna för de enhetliga 4-polytoper polytoper. Listan är inte bevisat fullständig.
Vanliga 5-polytoper
Vanliga 5-polytoper kan representeras av Schläfli-symbolen {p,q,r,s}, med s {p,q,r} 4-polytopfasetter runt varje yta . Det finns exakt tre sådana vanliga polytoper, alla konvexa:
- {3,3,3,3} - 5-simplex
- {4,3,3,3} - 5-kub
- {3,3,3,4} - 5-ortoplex
Det finns inga icke-konvexa vanliga polytoper i 5 dimensioner eller högre.
Konvexa enhetliga 5-polytoper
Vad är den kompletta uppsättningen av konvexa enhetliga 5-polytoper?
Det finns 104 kända konvexa enhetliga 5-polytoper, plus ett antal oändliga familjer av duoprismprismor och polygon-polyederduoprismor. Alla utom det stora antiprismatprismat är baserade på Wythoff-konstruktioner , reflektionssymmetri genererad med Coxeter-grupper . [ citat behövs ]
Symmetri av enhetliga 5-polytoper i fyra dimensioner
5 -simplex är den vanliga formen i A 5 -familjen. 5-kuben och 5 -ortoplexen är de vanliga formerna i B 5 -familjen. Den förgrenade grafen för D 5 -familjen innehåller 5-ortoplexet , såväl som en 5-demikub som är en alternerad 5-kub .
Varje reflekterande enhetlig 5-polytop kan konstrueras i en eller flera reflekterande punktgrupper i 5 dimensioner av en Wythoff-konstruktion , representerad av ringar runt permutationer av noder i ett Coxeter-diagram . Spegelhyperplan kan grupperas, sedda av färgade noder, åtskilda av jämna grenar . Symmetrigrupper av formen [a,b,b,a], har en utökad symmetri, [[a,b,b,a]], som [3,3,3,3], vilket fördubblar symmetriordningen. Enhetliga polytoper i denna grupp med symmetriska ringar innehåller denna utökade symmetri.
Om alla speglar av en given färg är oringade (inaktiva) i en given enhetlig polytop, kommer den att ha en lägre symmetrikonstruktion genom att ta bort alla de inaktiva speglarna. Om alla noder i en given färg är ringade (aktiva), kan en alterneringsoperation generera en ny 5-polytop med kiral symmetri, visad som "tomma" inringade noder, men geometrin är generellt inte justerbar för att skapa enhetliga lösningar.
- Grundläggande familjer
|
Gruppsymbol _ |
Beställa | Coxeter graf |
Klammernotation _ |
Kommutator undergrupp |
Coxeter nummer (h) |
Reflektioner m =5/2 h |
||
|---|---|---|---|---|---|---|---|---|
| En 5 | 720 | [3,3,3,3] | [3,3,3,3] + | 6 | 15 |
|||
| D 5 | 1920 | [3,3,3 1,1 ] | [3,3,3 1,1 ] + | 8 | 20 |
|||
| B 5 | 3840 | [4,3,3,3] | 10 | 5 |
20 |
|||
- Enhetliga prismor
Det finns 5 ändliga kategoriska enhetliga prismatiska familjer av polytoper baserade på de icke-prismatiska enhetliga 4-polytoperna . Det finns en oändlig familj av 5-polytoper baserad på prismor av de enhetliga duoprismerna {p}×{q}×{ }.
|
Coxeter grupp |
Beställa |
Coxeter diagram |
Coxeter notation |
Kommutator undergrupp |
Reflektioner | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A 4 A 1 | 120 | [3,3,3,2] = [3,3,3]×[ ] | [3,3,3] + | 10 |
1 |
||||||
| D 4 A 1 | 384 | [3 1,1,1 ,2] = [3 1,1,1 ]×[ ] | [3 1,1,1 ] + | 12 |
1 |
||||||
| B 4 A 1 | 768 | [4,3,3,2] = [4,3,3]×[ ] | 4 |
12 |
1 |
||||||
| F 4 A 1 | 2304 | [3,4,3,2] = [3,4,3]×[ ] | [3 + ,4,3 + ] | 12 |
12 |
1 |
|||||
| H 4 A 1 | 28800 | [5,3,3,2] = [3,4,3]×[ ] | [5,3,3] + | 60 |
1 |
||||||
| Duoprismatiska prismor (använd 2p och 2q för jämnt) | |||||||||||
| I 2 ( p ) I 2 ( q ) A 1 | 8 pq | [p,2,q,2] = [p]×[q]×[ ] | [p + ,2,q + ] |
sid |
q |
1 |
|||||
| I 2 (2 p ) I 2 ( q ) A 1 | 16 pq | [2p,2,q,2] = [2p]×[q]×[ ] | sid |
sid |
q |
1 |
|||||
| I 2 (2 p ) I 2 ( 2 q ) A 1 | 32 pq | [2p,2,2q,2] = [2p]×[2q]×[ ] |
sid |
sid |
q |
q |
1 |
||||
- Enhetliga duoprismer
Det finns 3 kategoriska enhetliga duoprismatiska familjer av polytoper baserade på kartesiska produkter av de enhetliga polyedrarna och regelbundna polygoner : { q , r }×{ p }.
|
Coxeter grupp |
Beställa |
Coxeter diagram |
Coxeter notation |
Kommutator undergrupp |
Reflektioner | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Prismatiska grupper (använd 2p för jämnt) | |||||||||||
| A 3 I 2 ( p ) | 48 sid | [3,3,2, p ] = [3,3]×[ p ] | [(3,3) + ,2, p + ] | 6 |
sid |
||||||
| A 3 I 2 ( 2p ) | 96 sid | [3,3,2,2 p ] = [3,3]×[2 p ] | 6 |
sid |
sid |
||||||
| B 3 I 2 ( p ) | 96 sid | [4,3,2, p ] = [4,3]×[ p ] | 3 |
6 |
sid |
||||||
| B 3 I 2 ( 2p ) | 192 sid | [4,3,2,2 p ] = [4,3]×[2 p ] | 3 |
6 |
sid |
sid |
|||||
| H 3 I 2 ( p ) | 240 sid | [5,3,2, p ] = [5,3]×[ p ] | [(5,3) + ,2, p + ] | 15 |
sid |
||||||
| H 3 I 2 ( 2p ) | 480 sid | [5,3,2,2 p ] = [5,3]×[2 p ] | 15 |
sid |
sid |
||||||
Räknar upp de konvexa enhetliga 5-polytoperna
-
Simplexfamilj : A 5 [3 4 ]
- 19 enhetliga 5-polytoper
-
Hyperkub / Ortoplex familj: B 5 [4,3 3 ]
- 31 enhetliga 5-polytoper
-
Demihypercube D 5 /E 5 familj: [3 2,1,1 ]
- 23 enhetliga 5-polytoper (8 unika)
- Polykorala prismor:
- 56 enhetliga 5-polytops (45 unika) konstruktioner baserade på prismatiska familjer: [3,3,3]×[ ], [4,3,3]×[ ], [5,3,3]×[ ], [3] 1,1,1 ]×[ ].
- En icke-Wythoffian - Det stora antiprismatprismat är den enda kända icke-Wythoffiska konvexa enhetliga 5-polytopen, konstruerad av två stora antiprismor förbundna med polyedriska prismor.
Det leder till: 19+31+8+45+1=104
Dessutom finns det:
- Oändligt många enhetliga 5-polytopkonstruktioner baserade på duoprismprismatiska familjer: [ p ]×[ q ]×[ ].
- Oändligt många enhetliga 5-polytopkonstruktioner baserade på duoprismatiska familjer: [3,3]×[ p ], [4,3]×[ p ], [5,3]×[ p ].
Familjen A 5
Det finns 19 former baserade på alla permutationer av Coxeter-diagrammen med en eller flera ringar. (16+4-1 fall)
De är namngivna av Norman Johnson från Wythoffs byggverksamhet på vanlig 5-simplex (hexateron).
A 5 - familjen har symmetri av ordningen 720 (6 factorial ). 7 av de 19 figurerna, med symmetriskt ringade Coxeter-diagram har dubblerad symmetri, ordning 1440.
Koordinaterna för enhetliga 5-polytoper med 5-simplex symmetri kan genereras som permutationer av enkla heltal i 6-rymden, allt i hyperplan med normal vektor (1,1,1,1,1,1).
| # | Baspunkt |
Johnsons namnsystem Bowers namn och (akronym) Coxeter-diagram |
k-face element räknas |
Vertex figur |
Fasetträkningar efter plats: [3,3,3,3] | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 3 | 2 | 1 | 0 |
[3,3,3] (6) |
[3,3,2] (15) |
[3,2,3] (20) |
[2,3,3] (15) |
[3,3,3] (6) |
Alt | ||||
| 1 | (0,0,0,0,0,1) eller (0,1,1,1,1,1) |
5-simplex hexateron (hix) |
6 | 15 | 20 | 15 | 6 |
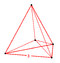 {3,3,3} |
 {3,3,3} |
- | - | - | - | |
| 2 | (0,0,0,0,1,1) eller (0,0,1,1,1,1) |
Rektifierad 5-simplex likriktad hexateron (rix) |
12 | 45 | 80 | 60 | 15 |
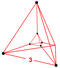 t{3,3}×{ } |
 r{3,3,3} |
- | - | - |
 {3,3,3} |
|
| 3 | (0,0,0,0,1,2) eller (0,1,2,2,2,2) |
Trunkerat 5-simplex trunkerat hexateron (tix) |
12 | 45 | 80 | 75 | 30 |
 Tetrah.pyr |
 t{3,3,3} |
- | - | - |
 {3,3,3} |
|
| 4 | (0,0,0,1,1,2) eller (0,1,1,2,2,2) |
Kantellerad 5-simplex liten romberad hexateron (sarx) |
27 | 135 | 290 | 240 | 60 |
prisma-kil |
 rr{3,3,3} |
- | - |
 { }×{3,3} |
 r{3,3,3} |
|
| 5 | (0,0,0,1,2,2) eller (0,0,1,2,2,2) |
Bitruncated 5-simplex bitruncated hexateron (bittix) |
12 | 60 | 140 | 150 | 60 |

|
 2t{3,3,3} |
- | - | - |
 t{3,3,3} |
|
| 6 | (0,0,0,1,2,3) eller (0,1,2,3,3,3) |
Cantitruncated 5-simplex stor romberad hexateron (garx) |
27 | 135 | 290 | 300 | 120 |
|
 tr{3,3,3} |
- | - |
 { }×{3,3} |
 t{3,3,3} |
|
| 7 | (0,0,1,1,1,2) eller (0,1,1,1,2,2) |
Runcinerad 5-simplex liten prismaterad hexateron (spix) |
47 | 255 | 420 | 270 | 60 |

|
 t 0,3 {3,3,3} |
- |
 {3}×{3} |
 { }×r{3,3} |
 r{3,3,3} |
|
| 8 | (0,0,1,1,2,3) eller (0,1,2,2,3,3) |
Runcitruncated 5-simplex prismatotruncated hexateron (pattix) |
47 | 315 | 720 | 630 | 180 |
|
 t 0,1,3 {3,3,3} |
- |
 {6}×{3} |
 { }×r{3,3} |
 rr{3,3,3} |
|
| 9 | (0,0,1,2,2,3) eller (0,1,1,2,3,3) |
Runcicantellated 5-simplex prismatorhombated hexateron (pirx) |
47 | 255 | 570 | 540 | 180 |
|
 t 0,1,3 {3,3,3} |
- |
 {3}×{3} |
 { }×t{3,3} |
 2t{3,3,3} |
|
| 10 | (0,0,1,2,3,4) eller (0,1,2,3,4,4) |
Runcicantitruncerad 5-simplex stor prismaterad hexateron (gippix) |
47 | 315 | 810 | 900 | 360 |
 Irr. 5-cell |
 t 0,1,2,3 {3,3,3} |
- |
 {3}×{6} |
 { }×t{3,3} |
 tr{3,3,3} |
|
| 11 | (0,1,1,1,2,3) eller (0,1,2,2,2,3) |
Steritrunkerad 5-simplex celliprismatad hexateron (cappix) |
62 | 330 | 570 | 420 | 120 |

|
 t{3,3,3} |
 { }×t{3,3} |
 {3}×{6} |
 { }×{3,3} |
 t 0,3 {3,3,3} |
|
| 12 | (0,1,1,2,3,4) eller (0,1,2,3,3,4) |
Stericantitruncated 5-simplex celligreatorhombated hexateron (cograx) |
62 | 480 | 1140 | 1080 | 360 |
|
 tr{3,3,3} |
 { }×tr{3,3} |
 {3}×{6} |
 { }×rr{3,3} |
 t 0,1,3 {3,3,3} |
|
| 13 | (0,0,0,1,1,1) |
Birectifierad 5-simplex dodecateron (prick) |
12 | 60 | 120 | 90 | 20 |
 {3}×{3} |
 r{3,3,3} |
- | - | - |
 r{3,3,3} |
|
| 14 | (0,0,1,1,2,2) |
Bikantellerad 5-simplex liten birhomberad dodecateron (sibrid) |
32 | 180 | 420 | 360 | 90 |

|
 rr{3,3,3} |
- |
 {3}×{3} |
- |
 rr{3,3,3} |
|
| 15 | (0,0,1,2,3,3) |
Bicantitruncated 5-simplex stor birhomberad dodecateron (gibrid) |
32 | 180 | 420 | 450 | 180 |
|
 tr{3,3,3} |
- |
 {3}×{3} |
- |
 tr{3,3,3} |
|
| 16 | (0,1,1,1,1,2) |
Stericerad 5-simplex liten cellad dodecateron (scad) |
62 | 180 | 210 | 120 | 30 |
 Irr. 16-celler |
 {3,3,3} |
 { }×{3,3} |
 {3}×{3} |
 { }×{3,3} |
 {3,3,3} |
|
| 17 | (0,1,1,2,2,3) |
Sterikantellerad 5-simplex liten cellirhomberad dodecateron (kort) |
62 | 420 | 900 | 720 | 180 |

|
 rr{3,3,3} |
 { }×rr{3,3} |
 {3}×{3} |
 { }×rr{3,3} |
 rr{3,3,3} |
|
| 18 | (0,1,2,2,3,4) |
Sterirunkat 5-simplex celliprismatotrunket dodecateron (captid) |
62 | 450 | 1110 | 1080 | 360 |
|
 t 0,1,3 {3,3,3} |
 { }×t{3,3} |
 {6}×{6} |
 { }×t{3,3} |
 t 0,1,3 {3,3,3} |
|
| 19 | (0,1,2,3,4,5) |
Omnitruncerad 5-simplex storcellad dodecateron (gocad) |
62 | 540 | 1560 | 1800 | 720 |
 Irr. {3,3,3} |
 t 0,1,2,3 {3,3,3} |
 { }×tr{3,3} |
 {6}×{6} |
 { }×tr{3,3} |
 t 0,1,2,3 {3,3,3} |
|
| Olikformigt |
Omnisnub 5-simplex snub dodecateron (snod) snub hexateron (snix) |
422 | 2340 | 4080 | 2520 | 360 | ht 0,1,2,3 {3,3,3} | ht 0,1,2,3 {3,3,2} | ht 0,1,2,3 {3,2,3} | ht 0,1,2,3 {3,3,2} | ht 0,1,2,3 {3,3,3} |
 (360) Irr. {3,3,3} |
||
Familjen B 5
B 5 - familjen har symmetri av ordningen 3840 (5!×2 5 ).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Denna familj har 2 5 −1=31 Wythoffian enhetliga polytoper genererade genom att markera en eller flera noder i Coxeter-diagrammet . Dessutom läggs till 8 enhetliga polytoper genererade som alternationer med halva symmetrin, som bildar en fullständig duplikat av D 5 -familjen som ... = ..... (Det finns fler alternationer som inte är listade eftersom de endast producerar upprepningar, som ... = .... och ... = .... Dessa skulle ge en fullständig duplicering av de enhetliga 5-polytoperna numrerade 20 till 34 med symmetri bruten på mitten.)
Denna familj har 2 5 −1=31 Wythoffian enhetliga polytoper genererade genom att markera en eller flera noder i Coxeter-diagrammet . Dessutom läggs till 8 enhetliga polytoper genererade som alternationer med halva symmetrin, som bildar en fullständig duplikat av D 5 -familjen som ... = ..... (Det finns fler alternationer som inte är listade eftersom de endast producerar upprepningar, som ... = .... och ... = .... Dessa skulle ge en fullständig duplicering av de enhetliga 5-polytoperna numrerade 20 till 34 med symmetri bruten på mitten.)
För enkelhetens skull är den uppdelad i två undergrupper, var och en med 12 former, och 7 "mellanformer" som hör hemma i båda.
5-kubfamiljen av 5-polytoper ges av de konvexa skroven på baspunkterna som anges i följande tabell, med alla permutationer av koordinater och tecken tagna. Varje baspunkt genererar en distinkt enhetlig 5-polytop. Alla koordinater motsvarar enhetliga 5-polytoper med kantlängd 2.
| # | Baspunkt |
Namn Coxeter diagram |
Element räknas |
Vertex figur |
Fasetträkningar efter plats: [4,3,3,3] | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 3 | 2 | 1 | 0 |
[4,3,3] (10) |
[4,3,2] (40) |
[4,2,3] (80) |
[2,3,3] (80) |
[3,3,3] (32) |
Alt | ||||
| 20 | (0,0,0,0,1)√2 |
5-ortoplex triacontaditeron (tac) |
32 | 80 | 80 | 40 | 10 |
 {3,3,4} |
- | - | - | - |
 {3,3,3} |
|
| 21 | (0,0,0,1,1)√2 |
Rektifierad 5-ortoplex rätad triacontaditeron (råtta) |
42 | 240 | 400 | 240 | 40 |
 { }×{3,4} |
 {3,3,4} |
- | - | - |
 r{3,3,3} |
|
| 22 | (0,0,0,1,2)√2 |
Trunkerat 5-ortoplex trunkerat triacontaditeron (tot) |
42 | 240 | 400 | 280 | 80 |
 (Octah.pyr) |
 {3,3,4} |
- | - | - |
 t{3,3,3} |
|
| 23 | (0,0,1,1,1)√2 |
Birektifierad 5-kub penteractitriacontaditeron (nit) (Birectified 5-ortoplex) |
42 | 280 | 640 | 480 | 80 |
 {4}×{3} |
 r{3,3,4} |
- | - | - |
 r{3,3,3} |
|
| 24 | (0,0,1,1,2)√2 |
Kantellerad 5-ortoplex liten romberad triacontaditeron (sart) |
82 | 640 | 1520 | 1200 | 240 |
 Prism-kil |
 r{3,3,4} |
 { }×{3,4} |
- | - |
 rr{3,3,3} |
|
| 25 | (0,0,1,2,2)√2 |
Bitruncated 5-ortoplex bitruncated triacontaditeron (bittit) |
42 | 280 | 720 | 720 | 240 |  |
 t{3,3,4} |
- | - | - |
 2t{3,3,3} |
|
| 26 | (0,0,1,2,3)√2 |
Cantitruncated 5-ortoplex stor romberad triacontaditeron (gart) |
82 | 640 | 1520 | 1440 | 480 |  |
 t{3,3,4} |
 { }×{3,4} |
- | - |
 t 0,1,3 {3,3,3} |
|
| 27 | (0,1,1,1,1)√2 |
Rektifierad 5-kubbar rätad penteract (rin) |
42 | 200 | 400 | 320 | 80 |
 {3,3}×{ } |
 r{4,3,3} |
- | - | - |
 {3,3,3} |
|
| 28 | (0,1,1,1,2)√2 |
Runcinerad 5-ortoplex liten prismaterad triacontaditeron (spat) |
162 | 1200 | 2160 | 1440 | 320 |  |
 r{4,3,3} |
 { }×r{3,4} |
 {3}×{4} |
 t 0,3 {3,3,3} |
||
| 29 | (0,1,1,2,2)√2 |
Bikantellerad 5-kub liten birhomberad penteractitriacontaditeron (sibrant) (Bicantellated 5-ortoplex) |
122 | 840 | 2160 | 1920 | 480 |  |
 rr{3,3,4} |
- |
 {4}×{3} |
- |
 rr{3,3,3} |
|
| 30 | (0,1,1,2,3)√2 |
Runcitruncated 5-ortoplex prismatotruncated triacontaditeron (pattit) |
162 | 1440 | 3680 | 3360 | 960 |  |
 rr{3,3,4} |
 { }×r{3,4} |
 {6}×{4} |
- |
 t 0,1,3 {3,3,3} |
|
| 31 | (0,1,2,2,2)√2 |
Bitruncated 5-kub bitruncated penteract (bittin) |
42 | 280 | 720 | 800 | 320 |  |
 2t{4,3,3} |
- | - | - |
 t{3,3,3} |
|
| 32 | (0,1,2,2,3)√2 |
Runcicantellated 5-ortoplex prismatorhombated triacontaditeron (pirt) |
162 | 1200 | 2960 | 2880 | 960 |  |
 2t{4,3,3} |
 { }×t{3,4} |
 {3}×{4} |
- |
 t 0,1,3 {3,3,3} |
|
| 33 | (0,1,2,3,3)√2 |
Bicantitruncated 5-cube great birhombated triacontaditeron (gibrant) (Bicantitruncated 5-ortoplex) |
122 | 840 | 2160 | 2400 | 960 |  |
 tr{3,3,4} |
- |
 {4}×{3} |
- |
 rr{3,3,3} |
|
| 34 | (0,1,2,3,4)√2 |
Runcicantitruncated 5-ortoplex great prismated triacontaditeron (gippit) |
162 | 1440 | 4160 | 4800 | 1920 |  |
 tr{3,3,4} |
 { }×t{3,4} |
 {6}×{4} |
- |
 t 0,1,2,3 {3,3,3} |
|
| 35 | (1,1,1,1,1) |
5-kub penteract (pent) |
10 | 40 | 80 | 80 | 32 |
 {3,3,3} |
 {4,3,3} |
- | - | - | - | |
| 36 |
(1,1,1,1,1) + (0,0,0,0,1)√2 |
Stericated 5-cube small cellated penteractitriacontaditeron (snålt) (stericated 5-ortoplex) |
242 | 800 | 1040 | 640 | 160 |
 Tetr.antiprm |
 {4,3,3} |
 {4,3}×{ } |
 {4}×{3} |
 { }×{3,3} |
 {3,3,3} |
|
| 37 |
(1,1,1,1,1) + (0,0,0,1,1)√2 |
Runcinerad 5-kub liten prismaterad penterakt (span) |
202 | 1240 | 2160 | 1440 | 320 |  |
 t 0,3 {4,3,3} |
- |
 {4}×{3} |
 { }×r{3,3} |
 r{3,3,3} |
|
| 38 |
(1,1,1,1,1) + (0,0,0,1,2)√2 |
Steritruncated 5-ortoplex celliprismated triacontaditeron (cappin) |
242 | 1520 | 2880 | 2240 | 640 | 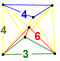 |
 t 0,3 {4,3,3} |
 {4,3}×{ } |
 {6}×{4} |
 { }×t{3,3} |
 t{3,3,3} |
|
| 39 |
(1,1,1,1,1) + (0,0,1,1,1)√2 |
Kantellerad 5-kub liten romberad penterakt (sirn) |
122 | 680 | 1520 | 1280 | 320 |
Prism-kil |
 rr{4,3,3} |
- | - |
 { }×{3,3} |
 r{3,3,3} |
|
| 40 |
(1,1,1,1,1) + (0,0,1,1,2)√2 |
Stericantellated 5-cube cellirhombated penteractitriacontaditeron (carnit) (stericantellated 5-ortoplex) |
242 | 2080 | 4720 | 3840 | 960 |  |
 rr{4,3,3} |
 rr{4,3}×{ } |
 {4}×{3} |
 { }×rr{3,3} |
 rr{3,3,3} |
|
| 41 |
(1,1,1,1,1) + (0,0,1,2,2)√2 |
Runcikantellerad 5-kubbar prismatorhomberad penteract (prin) |
202 | 1240 | 2960 | 2880 | 960 |  |
 t 0,2,3 {4,3,3} |
- |
 {4}×{3} |
 { }×t{3,3} |
 2t{3,3,3} |
|
| 42 |
(1,1,1,1,1) + (0,0,1,2,3)√2 |
Stericantitruncated 5-ortoplex celligreatorhombated triacontaditeron (cogart) |
242 | 2320 | 5920 | 5760 | 1920 |
 t 0,2,3 {4,3,3} |
 rr{4,3}×{ } |
 {6}×{4} |
 { }×tr{3,3} |
 tr{3,3,3} |
||
| 43 |
(1,1,1,1,1) + (0,1,1,1,1)√2 |
Trunkerad 5-kub stympad penteract (tan) |
42 | 200 | 400 | 400 | 160 |
 Tetrah.pyr |
 t{4,3,3} |
- | - | - |
 {3,3,3} |
|
| 44 |
(1,1,1,1,1) + (0,1,1,1,2)√2 |
Steritrunkerad 5-kubbar celliprismatad triacontaditeron (capt) |
242 | 1600 | 2960 | 2240 | 640 | 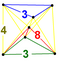 |
 t{4,3,3} |
 t{4,3}×{ } |
 {8}×{3} |
 { }×{3,3} |
 t 0,3 {3,3,3} |
|
| 45 |
(1,1,1,1,1) + (0,1,1,2,2)√2 |
Runcitruncated 5-kuber prismatotruncated penteract (pattin) |
202 | 1560 | 3760 | 3360 | 960 |  |
 t 0,1,3 {4,3,3} |
- |
 {8}×{3} |
 { }×r{3,3} |
 rr{3,3,3} |
|
| 46 |
(1,1,1,1,1) + (0,1,1,2,3)√2 |
Steriruncruncated 5-cube celliprismatotruncated penteractitriacontaditeron (captint) (Steriruncitruncated 5-ortoplex) |
242 | 2160 | 5760 | 5760 | 1920 |
 t 0,1,3 {4,3,3} |
 t{4,3}×{ } |
 {8}×{6} |
 { }×t{3,3} |
 t 0,1,3 {3,3,3} |
||
| 47 |
(1,1,1,1,1) + (0,1,2,2,2)√2 |
Cantitruncated 5-kub stor romberad penteract (girn) |
122 | 680 | 1520 | 1600 | 640 | 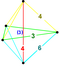 |
 tr{4,3,3} |
- | - |
 { }×{3,3} |
 t{3,3,3} |
|
| 48 |
(1,1,1,1,1) + (0,1,2,2,3)√2 |
Stericantitruncated 5-cube celligreatorhombated penteract (cogrin) |
242 | 2400 | 6000 | 5760 | 1920 |
 tr{4,3,3} |
 tr{4,3}×{ } |
 {8}×{3} |
 { }×rr{3,3} |
 t 0,1,3 {3,3,3} |
||
| 49 |
(1,1,1,1,1) + (0,1,2,3,3)√2 |
Runcicantitruncated 5-kub stor prismat penteract (gippin) |
202 | 1560 | 4240 | 4800 | 1920 |  |
 t 0,1,2,3 {4,3,3} |
- |
 {8}×{3} |
 { }×t{3,3} |
 tr{3,3,3} |
|
| 50 |
(1,1,1,1,1) + (0,1,2,3,4)√2 |
Omnitruncerad 5-kub stor cellad penteractitriacontaditeron (gacnet) (omnitruncated 5-ortoplex) |
242 | 2640 | 8160 | 9600 | 3840 |
 Irr. {3,3,3} |
 tr{4,3}×{ } |
 tr{4,3}×{ } |
 {8}×{6} |
 { }×tr{3,3} |
 t 0,1,2,3 {3,3,3} |
|
| 51 |
|
26 | 120 | 160 | 80 | 16 |
 r{3,3,3} |
 h{4,3,3} |
- | - | - | - |
 (16) {3,3,3} |
|
| 52 |
|
42 | 280 | 640 | 560 | 160 |

|
 h 2 {4,3,3} |
- | - | - |
 (16) r{3,3,3} |
 (16) t{3,3,3} |
|
| 53 |
|
42 | 360 | 880 | 720 | 160 |
 h 3 {4,3,3} |
- | - | - |
 (16) r{3,3,3} |
 (16) rr{3,3,3} |
||
| 54 |
|
82 | 480 | 720 | 400 | 80 |
 h{4,3,3} |
 h{4,3}×{} |
- | - |
 (16) {3,3,3} |
 (16) t 0,3 {3,3,3} |
||
| 55 |
|
42 | 360 | 1040 | 1200 | 480 |
 h 2,3 {4,3,3} |
- | - | - |
 (16) 2t{3,3,3} |
 (16) tr{3,3,3} |
||
| 56 |
|
82 | 720 | 1840 | 1680 | 480 |
 h 2 {4,3,3} |
 h 2 {4,3}×{} |
- | - |
 (16) rr{3,3,3} |
 (16) t 0,1,3 {3,3,3} |
||
| 57 |
|
82 | 560 | 1280 | 1120 | 320 |
 h 3 {4,3,3} |
 h{4,3}×{} |
- | - |
 (16) t{3,3,3} |
 (16) t 0,1,3 {3,3,3} |
||
| 58 |
|
82 | 720 | 2080 | 2400 | 960 |
 h 2,3 {4,3,3} |
 h 2 {4,3}×{} |
- | - |
 (16) tr{3,3,3} |
 (16) t 0,1,2,3 {3,3,3} |
||
| Olikformigt |
|
1122 | 6240 | 10880 | 6720 | 960 |
 sr{3,3,4} |
sr{2,3,4} | sr{3,2,4} | - | ht 0,1,2,3 {3,3,3} |
 (960) Irr. {3,3,3} |
||
| Olikformigt |
Edge-snub 5-orthoplex Pyritosnub penteract (pysnan) |
1202 | 7920 | 15360 | 10560 | 1920 | sr 3 {3,3,4} | sr 3 {2,3,4} | sr 3 {3,2,4} |
 s{3,3}×{ } |
ht 0,1,2,3 {3,3,3} |
 (960) Irr. {3,3}×{ } |
||
| Olikformigt |
Snub 5-kub Snub penteract (snan) |
2162 | 12240 | 21600 | 13440 | 960 | ht 0,1,2,3 {3,3,4} | ht 0,1,2,3 {2,3,4} | ht 0,1,2,3 {3,2,4} | ht 0,1,2,3 {3,3,2} | ht 0,1,2,3 {3,3,3} |
 (1920) Irr. {3,3,3} |
||
Familjen D 5
D 5 - familjen har symmetri av ordningen 1920 (5! x 2 4 ).
Denna familj har 23 Wythoffian enhetliga polytoper, från 3×8-1 permutationer av D 5 Coxeter diagrammet med en eller flera ringar. 15 (2×8-1) upprepas från B 5- familjen och 8 är unika för denna familj, även om även de 8 duplicerar växlingarna från B 5 -familjen.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() I de 15 upprepningarna ringas båda noderna som avslutar längd-1-grenarna, så de två typerna av element är identiska och symmetrin fördubblas: relationerna är ... = .... och ... = ... , vilket skapar en fullständig duplicering av de enhetliga 5-polytoperna 20 till 34 ovan. De 8 nya formerna har en sådan nod ringad och en inte, med relationen ... = ... duplicerar enhetliga 5-polytoper 51 till 58 ovan.
I de 15 upprepningarna ringas båda noderna som avslutar längd-1-grenarna, så de två typerna av element är identiska och symmetrin fördubblas: relationerna är ... = .... och ... = ... , vilket skapar en fullständig duplicering av de enhetliga 5-polytoperna 20 till 34 ovan. De 8 nya formerna har en sådan nod ringad och en inte, med relationen ... = ... duplicerar enhetliga 5-polytoper 51 till 58 ovan.
| # |
Coxeter diagram Schläfli symbol symboler Johnson och Bowers namn |
Element räknas |
Vertex figur |
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 3 | 2 | 1 | 0 |
[3,3,3] (16) |
[3 1,1,1 ] (10) |
[3,3]×[ ] (40) |
[ ]×[3]×[ ] (80) |
[3,3,3] (16) |
Alt | |||
| [51] |
= h{4,3,3,3}, 5-demikub Hemipenteract (hin) |
26 | 120 | 160 | 80 | 16 |
 r{3,3,3} |
 {3,3,3} |
 h{4,3,3} |
- | - | - | |
| [52] |
= h 2 {4,3,3,3}, kantisk 5-kub Trunkerad hemipenterakt (tunn) |
42 | 280 | 640 | 560 | 160 |

|
 t{3,3,3} |
 h 2 {4,3,3} |
- | - |
 r{3,3,3} |
|
| [53] |
= h 3 {4,3,3,3}, runkad 5-kub Liten romberad hemipenterakt (sirhin) |
42 | 360 | 880 | 720 | 160 |
 rr{3,3,3} |
 h 3 {4,3,3} |
- | - |
 r{3,3,3} |
||
| [54] |
= h 4 {4,3,3,3}, sterisk 5-kub Liten prismaterad hemipenterakt (sifin) |
82 | 480 | 720 | 400 | 80 |
 t 0,3 {3,3,3} |
 h{4,3,3} |
 h{4,3}×{} |
- |
 {3,3,3} |
||
| [55] |
= h 2,3 {4,3,3,3}, runcicantic 5-kub Stor romberad hemipenterakt (girhin) |
42 | 360 | 1040 | 1200 | 480 |
 2t{3,3,3} |
 h 2,3 {4,3,3} |
- | - |
 tr{3,3,3} |
||
| [56] |
= h 2,4 {4,3,3,3}, sterikantisk 5-kub Prismatotruncated hemipenteract (pithin) |
82 | 720 | 1840 | 1680 | 480 |
 t 0,1,3 {3,3,3} |
 h 2 {4,3,3} |
 h 2 {4,3}×{} |
- |
 rr{3,3,3} |
||
| [57] |
= h 3,4 {4,3,3,3}, steriruncic 5-kub Prismatorhombated hemipenteract (pirhin) |
82 | 560 | 1280 | 1120 | 320 |
 t 0,1,3 {3,3,3} |
 h 3 {4,3,3} |
 h{4,3}×{} |
- |
 t{3,3,3} |
||
| [58] |
= h 2,3,4 {4,3,3,3}, steriruncicantic 5-kub Stor prismaterad hemipenterakt (giphin) |
82 | 720 | 2080 | 2400 | 960 |
 t 0,1,2,3 {3,3,3} |
 h 2,3 {4,3,3} |
 h 2 {4,3}×{} |
- |
 tr{3,3,3} |
||
| Olikformigt |
= ht 0,1,2,3 {3,3,3,4}, alternerad runcicantitruncerad 5-ortoplex Snub hemipenteract (snahin) |
1122 | 6240 | 10880 | 6720 | 960 | ht 0,1,2,3 {3,3,3} |
 sr{3,3,4} |
sr{2,3,4} | sr{3,2,4} | ht 0,1,2,3 {3,3,3} |
 (960) Irr. {3,3,3} |
|
Enhetliga prismatiska former
Det finns 5 ändliga kategoriska enhetliga prismatiska familjer av polytoper baserade på de icke-prismatiska enhetliga 4-polytoperna . För enkelhetens skull visas inte de flesta alternativen.
A 4 × A 1
Denna prismatiska familj har 9 former :
A . 1 x A 4 -familjen har symmetri av storleksordningen 240 (2*5!)
| # |
Coxeter diagram och Schläfli symboler Namn |
Element räknas | ||||
|---|---|---|---|---|---|---|
| Fasett | Celler | Ansikten | Kanter | Vertices | ||
| 59 |
= {3,3,3}×{ } 5-cellsprisma (penp) |
7 | 20 | 30 | 25 | 10 |
| 60 |
= r{3,3,3}×{ } Riktat 5-cellsprisma (rappip) |
12 | 50 | 90 | 70 | 20 |
| 61 |
= t{3,3,3}×{ } Trunkerat 5-cellsprisma (tippip) |
12 | 50 | 100 | 100 | 40 |
| 62 |
= rr{3,3,3}×{ } Kantellerat 5-cellsprisma (srippip) |
22 | 120 | 250 | 210 | 60 |
| 63 |
= t 0,3 {3,3,3}×{ } Runcinerat 5-cellsprisma (spiddip) |
32 | 130 | 200 | 140 | 40 |
| 64 |
= 2t{3,3,3}×{ } Bitrunkerat 5-cellsprisma (decap) |
12 | 60 | 140 | 150 | 60 |
| 65 |
= tr{3,3,3}×{ } Cantitruncated 5-cells prisma (grippip) |
22 | 120 | 280 | 300 | 120 |
| 66 |
= t 0,1,3 {3,3,3}×{ } Runcitruncated 5-cellsprisma (prippip) |
32 | 180 | 390 | 360 | 120 |
| 67 |
= t 0,1,2,3 {3,3,3}×{ } Omnitruncated 5-cellsprisma (gippiddip) |
32 | 210 | 540 | 600 | 240 |
B 4 × A 1
Denna prismatiska familj har 16 former . (Tre delas med familjen [3,4,3]×[ ])
A . 1 ×B 4 -familjen har symmetri av storleksordningen 768 (2 5 4!)
De sista tre avstötningarna kan realiseras med lika långa kanter, men blir olikformiga ändå eftersom vissa av deras 4-ytor inte är enhetliga 4-polytoper.
| # |
Coxeter diagram och Schläfli symboler Namn |
Element räknas | ||||
|---|---|---|---|---|---|---|
| Fasett | Celler | Ansikten | Kanter | Vertices | ||
| [16] |
= {4,3,3}×{ } Tesseraktiskt prisma (pent) (samma som 5-kub ) |
10 | 40 | 80 | 80 | 32 |
| 68 |
= r{4,3,3}×{ } Riktat tesserasprisma (rittspets) |
26 | 136 | 272 | 224 | 64 |
| 69 |
= t{4,3,3}×{ } Trunkerat tesseraktiskt prisma (tattip) |
26 | 136 | 304 | 320 | 128 |
| 70 |
= rr{4,3,3}×{ } Kantellerat tesseraktiskt prisma (srittip) |
58 | 360 | 784 | 672 | 192 |
| 71 |
= t 0,3 {4,3,3}×{ } Runcinerat tesserasprisma (sidpithip) |
82 | 368 | 608 | 448 | 128 |
| 72 |
= 2t{4,3,3}×{ } Bitrunkerat tesseraktiskt prisma (tahp) |
26 | 168 | 432 | 480 | 192 |
| 73 |
= tr{4,3,3}×{ } Cantitruncated tesseractic prisma (grittop) |
58 | 360 | 880 | 960 | 384 |
| 74 |
= t 0,1,3 {4,3,3}×{ } Runcitruncated tesseractic prisma (prohp) |
82 | 528 | 1216 | 1152 | 384 |
| 75 |
= t 0,1,2,3 {4,3,3}×{ } Omnitruncated tesseractic prisma (gidpithip) |
82 | 624 | 1696 | 1920 | 768 |
| 76 |
= {3,3,4}×{ } 16-cellsprisma (hexip) |
18 | 64 | 88 | 56 | 16 |
| 77 |
= r{3,3,4}×{ } Riktat 16-cellsprisma (icope) (samma som 24-cellsprisma ) |
26 | 144 | 288 | 216 | 48 |
| 78 |
= t{3,3,4}×{ } Trunkerat 16-cellsprisma (thexip) |
26 | 144 | 312 | 288 | 96 |
| 79 |
= rr{3,3,4}×{ } Kantellerat 16-cellsprisma (ricope) (Samma som likriktat 24-cellsprisma ) |
50 | 336 | 768 | 672 | 192 |
| 80 |
= tr{3,3,4}×{ } Cantitruncated 16-cells prisma (ticope) (Samma som trunkerat 24-cells prisma ) |
50 | 336 | 864 | 960 | 384 |
| 81 |
= t 0,1,3 {3,3,4}×{ } Runcitruncated 16-cellsprisma (prittip) |
82 | 528 | 1216 | 1152 | 384 |
| 82 |
= sr{3,3,4}×{ } snub 24-cellsprisma (sadip) |
146 | 768 | 1392 | 960 | 192 |
| Olikformigt |
korrigerad tesseraktisk alterprisma (rita) |
50 | 288 | 464 | 288 | 64 |
| Olikformigt |
trunkerad 16-cells alterprisma (thexa) |
26 | 168 | 384 | 336 | 96 |
| Olikformigt |
bitruncated tesseractic alterprism (taha) |
50 | 288 | 624 | 576 | 192 |
F 4 × A 1
Denna prismatiska familj har 10 former .
A . 1 x F 4 -familjen har symmetri av ordningen 2304 (2*1152) Tre polytoper 85, 86 och 89 (grön bakgrund) har dubbel symmetri [[3,4,3],2], ordning 4608. Den sista, snubbla 24-cellsprisma, (blå bakgrund) har [3 + , 4 , 3,2] symmetri, order 1152.
| # |
Coxeter diagram och Schläfli symboler Namn |
Element räknas | ||||
|---|---|---|---|---|---|---|
| Fasetter | Celler | Ansikten | Kanter | Vertices | ||
| [77] |
= {3,4,3}×{ } 24-cellsprisma (icope) |
26 | 144 | 288 | 216 | 48 |
| [79] |
= r{3,4,3}×{} rätat 24-cellsprisma (rikop) |
50 | 336 | 768 | 672 | 192 |
| [80] |
= t{3,4,3}×{ } trunkerat 24-cellsprisma (ticop) |
50 | 336 | 864 | 960 | 384 |
| 83 |
= rr{3,4,3}×{ } kantellerat 24-cellsprisma (sricope) |
146 | 1008 | 2304 | 2016 | 576 |
| 84 |
= t 0,3 {3,4,3}×{ } runcinerat 24-cellsprisma (spiccup) |
242 | 1152 | 1920 | 1296 | 288 |
| 85 |
= 2t{3,4,3}×{ } bitrunkerat 24-cellsprisma (contip) |
50 | 432 | 1248 | 1440 | 576 |
| 86 |
= tr{3,4,3}×{ } cantitruncated 24-cells prisma (gricope) |
146 | 1008 | 2592 | 2880 | 1152 |
| 87 |
= t 0,1,3 {3,4,3}×{ } runcitruncated 24-cellsprisma (pricope) |
242 | 1584 | 3648 | 3456 | 1152 |
| 88 |
= t 0,1,2,3 {3,4,3}×{ } omnitruncerat 24-cellsprisma (gippiccup) |
242 | 1872 | 5088 | 5760 | 2304 |
| [82] |
= s{3,4,3}×{ } snub 24-cells prisma (sadip) |
146 | 768 | 1392 | 960 | 192 |
H 4 × A 1
Denna prismatiska familj har 15 former :
Familjen A 1 x H 4 . har symmetri av storleksordningen 28800 (2*14400)
| # |
Coxeter diagram och Schläfli symboler Namn |
Element räknas | ||||
|---|---|---|---|---|---|---|
| Fasetter | Celler | Ansikten | Kanter | Vertices | ||
| 89 |
= {5,3,3}×{ } 120-cells prisma (höft) |
122 | 960 | 2640 | 3000 | 1200 |
| 90 |
= r{5,3,3}×{ } Riktat 120-cellsprisma (rahipe) |
722 | 4560 | 9840 | 8400 | 2400 |
| 91 |
= t{5,3,3}×{ } Trunkerat 120-cellsprisma (topp) |
722 | 4560 | 11040 | 12 000 | 4800 |
| 92 |
= rr{5,3,3}×{ } Kantellerat 120-cellsprisma (srahip) |
1922 | 12960 | 29040 | 25200 | 7200 |
| 93 |
= t 0,3 {5,3,3}×{ } Runcinerat 120-cellsprisma (sidpixhip) |
2642 | 12720 | 22080 | 16800 | 4800 |
| 94 |
= 2t{5,3,3}×{ } Bitrunkerat 120-cellsprisma (xhip) |
722 | 5760 | 15840 | 18 000 | 7200 |
| 95 |
= tr{5,3,3}×{ } Cantitruncated 120-cells prisma (grahip) |
1922 | 12960 | 32640 | 36 000 | 14400 |
| 96 |
= t 0,1,3 {5,3,3}×{ } Runcitruncated 120-cells prisma (prixip) |
2642 | 18720 | 44880 | 43200 | 14400 |
| 97 |
= t 0,1,2,3 {5,3,3}×{ } Omnitruncated 120-cells prisma (gidpixhip) |
2642 | 22320 | 62880 | 72 000 | 28800 |
| 98 |
= {3,3,5}×{ } 600-cells prisma (exip) |
602 | 2400 | 3120 | 1560 | 240 |
| 99 |
= r{3,3,5}×{ } Riktat 600-cellsprisma (roxip) |
722 | 5040 | 10800 | 7920 | 1440 |
| 100 |
= t{3,3,5}×{ } Trunkerat 600-cells prisma (texip) |
722 | 5040 | 11520 | 10080 | 2880 |
| 101 |
= rr{3,3,5}×{ } Kantellerat 600-cells prisma (srixip) |
1442 | 11520 | 28080 | 25200 | 7200 |
| 102 |
= tr{3,3,5}×{ } Cantitruncated 600-cells prisma (grixip) |
1442 | 11520 | 31680 | 36 000 | 14400 |
| 103 |
= t 0,1,3 {3,3,5}×{ } Runcitruncated 600-cells prisma (prahip) |
2642 | 18720 | 44880 | 43200 | 14400 |
Duoprism prismor
Uniforma duoprismprismor, { p }×{ q }×{ }, bildar en oändlig klass för alla heltal p , q >2. {4}×{4}×{ } gör en lägre symmetriform av 5-kuben .
| Coxeter diagram | Namn | Element räknas | |||||
|---|---|---|---|---|---|---|---|
| 4-ansikten | Celler | Ansikten | Kanter | Vertices | |||
| { p }×{ q }×{ } | p + q +2 | 3 pq +3 p +3 q | 4 pq +2 p +2 q | 5 pq | 2 pq | ||
| { p } 2 × { } | 2( p +1) | 3 p ( p +1) | 4 p ( p +1) | 5 p 2 | 2 p 2 | ||
| {3} 2 ×{ } | 8 | 36 | 48 | 45 | 18 | ||
| {4} 2 ×{ } = 5-kub | 10 | 40 | 80 | 80 | 32 | ||
Stora antiprisma prisma
 Det stora antiprismatprismat är den enda kända konvexa icke-wythoffska enhetliga 5-polytopen. Den har 200 vertikaler, 1100 kanter, 1940 ansikten (40 pentagoner, 500 rutor, 1400 trianglar), 1360 celler (600 tetrahedra , 40 pentagonala antipler , 700 triangulära prismor , 20 pentagonala prismor ) och 322 hypercells (2 Grand Antiprism , 700 pentagonal , 20 pentagonal antiprismor och 300 tetraedriska prismor ) .
Det stora antiprismatprismat är den enda kända konvexa icke-wythoffska enhetliga 5-polytopen. Den har 200 vertikaler, 1100 kanter, 1940 ansikten (40 pentagoner, 500 rutor, 1400 trianglar), 1360 celler (600 tetrahedra , 40 pentagonala antipler , 700 triangulära prismor , 20 pentagonala prismor ) och 322 hypercells (2 Grand Antiprism , 700 pentagonal , 20 pentagonal antiprismor och 300 tetraedriska prismor ) . 

| # | namn | Element räknas | ||||
|---|---|---|---|---|---|---|
| Fasetter | Celler | Ansikten | Kanter | Vertices | ||
| 104 | grand antiprisma prisma (gappip) | 322 | 1360 | 1940 | 1100 | 200 |
Anteckningar om Wythoff-konstruktionen för de enhetliga 5-polytoperna
Konstruktionen av de reflekterande 5-dimensionella likformiga polytoperna görs genom en Wythoff-konstruktionsprocess och representeras genom ett Coxeter-diagram , där varje nod representerar en spegel. Noder ringas för att antyda vilka speglar som är aktiva. Hela uppsättningen av enhetliga polytoper som genereras är baserade på de unika permutationerna av ringade noder. Uniforma 5-polytoper benämns i förhållande till de vanliga polytoperna i varje familj. Vissa familjer har två vanliga konstruktörer och kan därför ha två sätt att namnge dem.
Här är de primära operatorerna som är tillgängliga för att konstruera och namnge de enhetliga 5-polytoperna.
Den sista operationen, snubben, och mer allmänt alterneringen, är operationen som kan skapa icke-reflekterande former. Dessa är ritade med "ihåliga ringar" vid noderna.
De prismatiska formerna och förgrenade graferna kan använda samma trunkeringsindexeringsnotation, men kräver ett explicit numreringssystem på noderna för tydlighetens skull.
| Drift |
Utökad Schläfli-symbol |
Coxeter diagram | Beskrivning | |
|---|---|---|---|---|
| Förälder | 0 t {p,q,r,s} | {p,q,r,s} |
|
Vilken vanlig 5-polytop som helst |
| Rättad till | t 1 {p,q,r,s} | r{p,q,r,s} |
|
Kanterna är helt trunkerade till enstaka punkter. 5-polytopen har nu de kombinerade ansiktena av förälder och dubbel. |
| Birectified | t 2 {p,q,r,s} | 2r{p,q,r,s} |
|
Birektifiering reducerar ansikten till punkter, celler till sina dualer . |
| Trekorrigerad | t 3 {p,q,r,s} | 3r{p,q,r,s} |
|
Trirectification reducerar celler till poäng. (Dubbel rättelse) |
| Fyrriktad | t 4 {p,q,r,s} | 4r{p,q,r,s} |
|
Fyrrättning reducerar 4-ansikten till poäng. (Dubbel) |
| Trunkerad | t 0,1 {p,q,r,s} | t{p,q,r,s} |
|
Varje ursprunglig vertex skärs av, med ett nytt ansikte som fyller gapet. Trunkering har en grad av frihet, som har en lösning som skapar en enhetlig trunkerad 5-polytop. 5-polytopen har sina ursprungliga ytor dubblerade på sidorna och innehåller sidorna av dualen.
|
| Kantellerad | t 0,2 {p,q,r,s} | rr{p,q,r,s} |
|
Förutom vertexstympning är varje originalkant avfasad med nya rektangulära ytor som dyker upp på deras plats. 
|
| Runcinerad | t 0,3 {p,q,r,s} |
|
Runcination reducerar celler och skapar nya celler vid hörn och kanter. | |
| Sterikerad | t 0,4 {p,q,r,s} | 2r2r{p,q,r,s} |
|
Sterikering minskar fasetter och skapar nya fasetter (hyperceller) vid hörn och kanter i mellanrummen. (Samma som expansionsoperation för 5-polytoper.) |
| Omnitruncerad | t 0,1,2,3,4 {p,q,r,s} |
|
Alla fyra operatorerna trunkering, kantellering, runcinering och sterikering tillämpas. | |
| Halv | h{2p,3,q,r} |
|
Alternering , samma som |
|
| Cantic | h 2 {2p,3,q,r} |
|
Samma som |
|
| Runcic | h 3 {2p,3,q,r} |
|
Samma som |
|
| Runcicantic | h 2,3 {2p,3,q,r} |
|
Samma som |
|
| Sterisk | h 4 {2p,3,q,r} |
|
Samma som |
|
| Steriruncic | h 3,4 {2p,3,q,r} |
|
Samma som |
|
| Sterikantiskt | h 2,4 {2p,3,q,r} |
|
Samma som |
|
| Steriruncicantic | h 2,3,4 {2p,3,q,r} |
|
Samma som |
|
| Nonchalera | s{p,2q,r,s} |
|
Alternerad trunkering | |
| Snub rättad | sr{p,q,2r,s} |
|
Omväxlande trunkerad rättelse | |
| ht 0,1,2,3 {p,q,r,s} |
|
Alternerad runcicantruncation | ||
| Full snubb | ht 0,1,2,3,4 {p,q,r,s} |
|
Alternerad omnitrunkation | |
Regelbundna och enhetliga bikakor
Det finns fem grundläggande affina Coxeter-grupper och 13 prismatiska grupper som genererar regelbundna och enhetliga tesselleringar i euklidiskt 4-rum.
| # | Coxeter grupp | Coxeter diagram | Blanketter | ||
|---|---|---|---|---|---|
| 1 | [3 [5] ] | [(3,3,3,3,3)] | 7 | ||
| 2 | [4,3,3,4] | 19 | |||
| 3 | [4,3,3 1,1 ] | [4,3,3,4,1 + ] |
|
23 (8 nya) | |
| 4 | [3 1,1,1,1 ] | [1 + ,4,3,3,4,1 + ] |
|
9 (0 nya) | |
| 5 | [3,4,3,3] | 31 (21 nya) | |||
Det finns tre vanliga bikakor av Euklidisk 4-utrymme:
-















 tesseractic honeycomb , med symbolerna {4,3,3,4}, = . Det finns 19 enhetliga honeycombs i denna familj.
tesseractic honeycomb , med symbolerna {4,3,3,4}, = . Det finns 19 enhetliga honeycombs i denna familj. -








 24-cells honungskaka , med symbolerna {3,4,3,3}, . Det finns 31 reflekterande enhetliga bikakor i denna familj, och en omväxlande form.
24-cells honungskaka , med symbolerna {3,4,3,3}, . Det finns 31 reflekterande enhetliga bikakor i denna familj, och en omväxlande form. -
Stympad 24-cells honungskaka med symbolerna t{3,4,3,3},









-

















 Snub 24-cells honeycomb , med symbolerna s{3,4,3,3}, och konstruerad av fyra snub 24-celler , en 16-cell och fem 5-celler vid varje vertex.
Snub 24-cells honeycomb , med symbolerna s{3,4,3,3}, och konstruerad av fyra snub 24-celler , en 16-cell och fem 5-celler vid varje vertex.
-
Stympad 24-cells honungskaka med symbolerna t{3,4,3,3},
-
16-cells honungskaka , med symbolerna {3,3,4,3},









Andra familjer som genererar enhetliga bikakor:
-








 Det finns 23 unikt ringade former, 8 nya i 16-cells bikakefamiljen. Med symbolerna h{4,3 2 , 4} är den geometriskt identisk med den 16-celliga bikakan , =
Det finns 23 unikt ringade former, 8 nya i 16-cells bikakefamiljen. Med symbolerna h{4,3 2 , 4} är den geometriskt identisk med den 16-celliga bikakan , = 






-




 Det finns 7 unikt ringade former från familjen , helt nya, inklusive:
Det finns 7 unikt ringade former från familjen , helt nya, inklusive:
-
































 Det finns 9 unikt ringade former i : [3 1,1,1,1 ] familjen, två nya, inklusive den fjärde tesseractic honeycomb , = , och den bitrunkerade tesseraktiska honungskakan , = .
Det finns 9 unikt ringade former i : [3 1,1,1,1 ] familjen, två nya, inklusive den fjärde tesseractic honeycomb , = , och den bitrunkerade tesseraktiska honungskakan , = .
Icke-wythoffska likformiga tesselleringar i 4-utrymme existerar också genom förlängning (införande av skikt) och gyration (roterande skikt) från dessa reflekterande former.
| # | Coxeter grupp | Coxeter diagram | |
|---|---|---|---|
| 1 | × | [4,3,4,2,∞] |
|
| 2 | × | [4,3 1,1 ,2,∞] |
|
| 3 | × | [3 [4] , 2,∞] |
|
| 4 | × x | [4,4,2,∞,2,∞] |
|
| 5 | × x | [6,3,2,∞,2,∞] |
|
| 6 | × x | [3 [3] ,2,∞,2,∞] |
|
| 7 | × x x | [∞,2,∞,2,∞,2,∞] |
|
| 8 | x | [3 [3] ,2,3 [3] ] |
|
| 9 | × | [3 [3] ,2,4,4] |
|
| 10 | × | [3 [3] ,2,6,3] |
|
| 11 | × | [4,4,2,4,4] |
|
| 12 | × | [4,4,2,6,3] |
|
| 13 | × | [6,3,2,6,3] |
|
Regelbundna och enhetliga hyperboliska bikakor
- Hyperboliska kompakta grupper
Det finns 5 kompakta hyperboliska Coxeter-grupper av rang 5, som var och en genererar enhetliga bikakor i hyperboliskt 4-utrymme som permutationer av ringar i Coxeter-diagrammen.
|
= [(3,3,3,3,4)]: |
= [5,3,3 1,1 ]: |
= [3,3,3,5]:
|
Det finns 5 vanliga kompakta konvexa hyperboliska bikakor i H 4 -utrymmet:
| Honeycomb namn |
Schläfli -symbol {p,q,r,s} |
Coxeter diagram |
Fasetttyp {p,q,r } |
Celltyp {p,q } |
Ansiktstyp { p} |
Ansiktsfigur {s } |
Kantfigur {r,s } |
Hönsfigur {q,r , s} |
Dubbel |
|---|---|---|---|---|---|---|---|---|---|
| Order-5 5-celler (pente) | {3,3,3,5} | {3,3,3} | {3,3} | {3} | {5} | {3,5} | {3,3,5} | {5,3,3,3} | |
| Order-3 120-cell (hitte) | {5,3,3,3} | {5,3,3} | {5,3} | {5} | {3} | {3,3} | {3,3,3} | {3,3,3,5} | |
| Order-5 tesseractic (pitest) | {4,3,3,5} | {4,3,3} | {4,3} | {4} | {5} | {3,5} | {3,3,5} | {5,3,3,4} | |
| Order-4 120-celler (shit) | {5,3,3,4} | {5,3,3} | {5,3} | {5} | {4} | {3,4} | {3,3,4} | {4,3,3,5} | |
| Order-5 120-celler (phitte) | {5,3,3,5} | {5,3,3} | {5,3} | {5} | {5} | {3,5} | {3,3,5} | Självdubbel |
Det finns också 4 vanliga kompakta hyperboliska stjärnbikakor i H 4 -utrymmet:
| Honeycomb namn |
Schläfli -symbol {p,q,r,s} |
Coxeter diagram |
Fasetttyp {p,q , r} |
Celltyp {p,q } |
Ansiktstyp { p} |
Ansiktsfigur {s } |
Kantfigur {r,s } |
Hönsfigur {q,r , s} |
Dubbel |
|---|---|---|---|---|---|---|---|---|---|
| Order-3 små stellerade 120-celler | {5/2,5,3,3} | {5/2,5,3} | {5/2,5} | {5} | {5} | {3,3} | {5,3,3} | {3,3,5,5/2} | |
| Order-5/2 600-cell | {3,3,5,5/2} | {3,3,5} | {3,3} | {3} | {5/2} | {5,5/2} | {3,5,5/2} | {5/2,5,3,3} | |
| Order-5 icosahedral 120-cell | {3,5,5/2,5} | {3,5,5/2} | {3,5} | {3} | {5} | {5/2,5} | {5,5/2,5} | {5,5/2,5,3} | |
| Order-3 stora 120-celler | {5,5/2,5,3} | {5,5/2,5} | {5,5/2} | {5} | {3} | {5,3} | {5/2,5,3} | {3,5,5/2,5} |
- Hyperboliska parakompakta grupper
Det finns 9 parakompakta hyperboliska Coxeter-grupper av rang 5, som var och en genererar enhetliga bikakor i 4-mellanrum som permutationer av ringar i Coxeter-diagrammen. Paracompact-grupper genererar bikakor med oändliga facetter eller vertexfigurer .
|
= [3,3 [4] ]:
|
|
= [3,4,3,4]: |
Anteckningar
- T. Gosset : On the Regular and Semi-Regular Figures in Space of n Dimensions , Messenger of Mathematics , Macmillan, 1900 (3 reguljära och en semiregular 4-polytop)
- A. Boole Stott : Geometrisk deduktion av semiregular från vanliga polytoper och rymdfyllningar , Verhandelingen av Koninklijke academy van Wetenschappen width unit Amsterdam, Eerste Sectie 11,1, Amsterdam, 1910
-
HSM Coxeter :
- HSM Coxeter , Regular Polytopes , 3:e upplagan, Dover New York, 1973 (sid. 297 Grundläggande regioner för irreducerbara grupper genererade av reflektioner, sfäriska och euklidiska)
- HSM Coxeter , The Beauty of Geometry: Tolv uppsatser (Kapitel 10: Regelbundna bikakor i hyperboliskt utrymme, Sammanfattningstabeller IV s213)
-
Kaleidoscopes: Selected Writings of HSM Coxeter , redigerad av F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Papper 22) HSM Coxeter, Regular and Semi Regular Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Papper 23) HSM Coxeter, Regular and Semi-Regular Polytopes II , [Math. Zeit. 188 (1985) 559-591] (s. 287 5D Euklidiska grupper, s. 298 Fyrdimensionella honeycombs)
- (Papper 24) HSM Coxeter, Regular and Semi-Regular Polytopes III , [Math. Zeit. 200 (1988) 3-45]
- NW Johnson : Theory of Uniform Polytopes and Honeycombs , Ph.D. Avhandling, University of Toronto, 1966
- James E. Humphreys, Reflection Groups and Coxeter Groups , Cambridge studies in advanced mathematics, 29 (1990) (Sida 141, 6.9 Lista över hyperboliska Coxeter-grupper, figur 2) [2 ]
externa länkar
- Klitzing, Richard. "5D enhetliga polytoper (polytera)" . – inkluderar icke-konvexa former samt dubbla konstruktioner från familjerna B 5 och D 5
| Plats | Familj | / / | ||||
|---|---|---|---|---|---|---|
| E 2 | Enhetlig plattsättning | {3 [3] } | δ 3 | hδ 3 | qδ 3 | Hexagonal |
| E 3 | Enhetlig konvex bikaka | {3 [4] } | δ 4 | hδ 4 | qδ 4 | |
| E 4 | Uniform 4-honeycomb | {3 [5] } | δ 5 | hδ 5 | qδ 5 | 24-cells honungskaka |
| E 5 | Uniform 5-bikaka | {3 [6] } | δ 6 | hδ 6 | qδ 6 | |
| E 6 | Uniform 6-honeycomb | {3 [7] } | δ 7 | hδ 7 | qδ 7 | 2 22 |
| E 7 | Uniform 7-honeycomb | {3 [8] } | δ 8 | hδ 8 | qδ 8 | 1 33 • 3 31 |
| E 8 | Uniform 8-honeycomb | {3 [9] } | δ 9 | hδ 9 | qδ 9 | 1 52 • 2 51 • 5 21 |
| E 9 | Uniform 9-honeycomb | {3 [10] } | δ 10 | hδ 10 | qδ 10 | |
| E 10 | Uniform 10-honeycomb | {3 [11] } | δ 11 | hδ 11 | qδ 11 | |
| E n -1 | Uniform ( n -1)- honeycomb | {3 [n] } | 5 n | hδ n | qδ n | 1 k2 • 2 k1 • k 21 |