Honeycomb (geometri)

Inom geometri är en honeycomb en utrymmesfyllning eller tät packning av polyedriska eller högre dimensionella celler , så att det inte finns några luckor. Det är ett exempel på den mer allmänna matematiska plattsättningen eller tessellationen i valfritt antal dimensioner. Dess dimension kan förtydligas som n -bikaka för en bikaka med n -dimensionell rymd.

Bikakor är vanligtvis konstruerade i vanligt euklidiskt ("platt") utrymme. De kan också konstrueras i icke-euklidiska utrymmen , såsom hyperboliska bikakor . Vilken ändlig enhetlig polytop som helst kan projiceras till sin omkrets för att bilda en enhetlig bikaka i sfäriskt utrymme.

Det är möjligt att fylla planet med polygoner som inte möts i sina hörn, till exempel med hjälp av rektanglar , som i ett tegelväggsmönster : detta är inte en korrekt plattsättning eftersom hörnen ligger halvvägs längs kanten på en intilliggande polygon. På samma sätt, i en riktig bikaka, får det inte finnas några kanter eller hörn som ligger en bit längs ytan av en intilliggande cell. Genom att tolka varje tegelyta som en hexagon med två inre vinklar på 180 grader kan mönstret betraktas som en riktig plattsättning. Men inte alla geometrar accepterar sådana hexagoner.

Klassificering

Det finns oändligt många bikakor, som bara delvis har klassificerats. De mer vanliga har tilldragit sig mest intresse, medan ett rikt och varierat utbud av andra fortsätter att upptäckas.

De enklaste bikakorna att bygga är bildade av staplade lager eller plattor av prismor baserat på några tesselleringar av planet. Speciellt för varje parallellepiped kan kopior fylla utrymmet, där den kubiska bikakan är speciell eftersom den är den enda vanliga bikakan i det vanliga (euklidiska) rymden. En annan intressant familj är Hill-tetraedrarna och deras generaliseringar, som också kan belägga utrymmet.

Enhetliga 3-bikakor

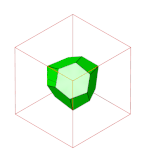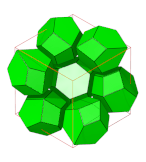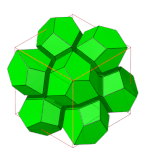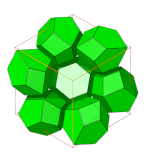
En 3-dimensionell enhetlig honeycomb är en honeycomb i 3-rymden som består av enhetliga polyedriska celler , och som har alla hörn desamma (dvs gruppen av [isometrier av 3-utrymme som bevarar plattsättningen] är transitiv på hörn ). Det finns 28 konvexa exempel i det euklidiska 3-utrymmet, även kallat Arkimedeiska honungskakor .

En honeycomb kallas regelbunden om gruppen av isometrier som bevarar plattsättningen verkar transitivt på flaggor, där en flagga är en vertex som ligger på en kant som ligger på en yta som ligger på en cell. Varje vanlig honungskaka är automatiskt enhetlig. Det finns dock bara en vanlig honeycomb i Euclidian 3-space, den kubiska honeycomb . Två är kvasiregelbundna (gjorda av två typer av vanliga celler):

Typ	Vanlig kubisk honungskaka	Kvasiregelbundna bikakor
Celler	Kubisk	Oktaedrar och tetraedrar
Platta lager

De tetraedriska-oktaedriska bikakorna och de roterande tetraedriska-oktaedriska bikakorna genereras av 3 eller 2 positioner av skivskikt av celler, var och en omväxlande tetraedrar och oktaedrar. Ett oändligt antal unika vaxkakor kan skapas genom högre ordning av mönster för att upprepa dessa skivskikt.

Rymdfyllande polyedrar

En bikaka med alla celler identiska inom sina symmetrier sägs vara celltransitiv eller isokorisk . I det 3-dimensionella euklidiska rymden sägs en cell av en sådan bikaka vara en rymdfyllande polyeder . Ett nödvändigt villkor för att en polyeder ska vara en rymdfyllande polyeder är att dess Dehn-invariant måste vara noll, vilket utesluter något av de platoniska fasta ämnena förutom kuben.

Fem rymdfyllande polyedrar kan tessellate 3-dimensionell euklidisk rymd med endast översättningar. De kallas parallelloedrar :

Kubisk honungskaka (eller varianter: kubisk , rhombisk hexaeder eller parallellepiped )
Sexkantig prismatisk bikaka
Rombisk dodekaedrisk honungskaka
Långsträckt dodekaedrisk honungskaka
Bitruncated kubisk honungskaka eller trunkerade oktaedrar

Kub (parallelpiped)	Sexkantigt prisma	Rombisk dodekaeder	Långsträckt dodekaeder	Stympad oktaeder
kubisk honungskaka	Sexkantig prismatisk bikaka	Rombiska dodekaedrar	Avlånga dodekaedrar	Stympade oktaedrar

3 kantlängder	3+1 kantlängder	4 kantlängder	4+1 kantlängder	6 kantlängder

Andra kända exempel på rymdfyllande polyedrar inkluderar:

Den triangulära prismatiska bikakan
Den roterande triangulära prismatiska bikakan
Triakis stympad tetraedrisk honungskaka . Voronoi-cellerna i kolatomerna i diamant har denna form.
Den trapetsrombiska dodekaedriska honungskakan
Isoedriska plattor

Andra bikakor med två eller flera polyedrar

Ibland kan två eller flera olika polyedrar kombineras för att fylla utrymmet. Förutom många av de enhetliga bikakorna är ett annat välkänt exempel Weaire-Phelan-strukturen , antagen från strukturen av klatrathydratkristaller

Den periodiska enheten för Weaire-Phelan-strukturen .

P8 tiling (with left and right-handed cells)

En bikaka av vänster- och högerhänta versioner av samma polyeder.

Icke-konvexa 3-bikakor

Dokumenterade exempel är sällsynta. Två klasser kan särskiljas:

Icke-konvexa celler som packas utan att överlappa varandra, analogt med plattsättningar av konkava polygoner. Dessa inkluderar en packning av den lilla stjärnformade rombiska dodekaedern , som i Yoshimoto-kuben .
Överlappning av celler vars positiva och negativa densiteter "upphäver" för att bilda ett jämnt tätt kontinuum, analogt med överlappande plattsättningar av planet.

Hyperboliska honungskakor

I 3-dimensionell hyperbolisk rymd beror den dihedrala vinkeln på en polyeder på dess storlek. De vanliga hyperboliska bikakorna inkluderar alltså två med fyra eller fem dodekaedrar som möts vid varje kant; deras dihedriska vinklar är alltså π/2 och 2π/5, som båda är mindre än en euklidisk dodekaeder. Bortsett från denna effekt följer de hyperboliska bikakorna samma topologiska begränsningar som euklidiska vaxkakor och polychora.

De 4 kompakta och 11 parakompakta vanliga hyperboliska bikakorna och många kompakta och parakompakta enhetliga hyperboliska bikakorna har räknats upp.

Fyra vanliga kompakta honungskakor i H ³
{5,3,4}	{4,3,5}	{3,5,3}	{5,3,5}

11 paracompact vanliga honungskakor
{6,3,3}	{6,3,4}	{6,3,5}	{6,3,6}	{4,4,3}	{4,4,4}
{3,3,6}	{4,3,6}	{5,3,6}	{3,6,3}	{3,4,4}

Dualitet av 3-bikakor

För varje bikaka finns en dubbel bikaka, som kan erhållas genom att byta:

celler för hörn.

ytor för kanter.

Detta är bara reglerna för att dualisera fyrdimensionella 4 -polytoper , förutom att den vanliga ändliga metoden för reciprokering kring en koncentrisk hypersfär kan stöta på problem.

De mer vanliga bikakorna dualiserar snyggt:

Den kubiska honungskakan är självdubbel.
Det för oktaedrar och tetraedrar är dubbelt med det för rombiska dodekaedrar.
Plattans honungskakor som härrör från enhetliga plana plattsättningar är dubbla till varandra på samma sätt som plattorna är.
Dualerna av de återstående arkimediska bikakorna är alla celltransitiva och har beskrivits av Inchbald.

Självdubbla honungskakor

Honeycombs kan också vara självdubbla . Alla n -dimensionella hyperkubiska bikakor med Schläfli-symboler {4,3 ^{n −2} ,4}, är självduala.

Se även

Vidare läsning

Coxeter, HSM : Vanliga polytoper .
Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design . Dover Publications, Inc. s. 164–199. ISBN 0-486-23729-X . Kapitel 5: Polyederpackning och utrymmesfyllning
Critchlow, K.: Ordning i rymden .
Pearce, P.: Struktur i naturen är en strategi för design .
Goldberg, Michael Three Infinite Families of Tetrahedral Space-Fillers Journal of Combinatorial Theory A, 16, s. 348–354, 1974.
Goldberg, Michael (1972). "Den rymdfyllande pentaedran" . Journal of Combinatorial Theory, serie A . 13 (3): 437–443. doi : 10.1016/0097-3165(72)90077-5 .
Goldberg, Michael The Space-filling Pentahedra II , Journal of Combinatorial Theory 17 (1974), 375–378.
Goldberg, Michael (1977). "På den rymdfyllande hexaedran". Geometriae Dedicata . 6 . doi : 10.1007/BF00181585 . S2CID 189889869 .
Goldberg, Michael (1978). "På de rymdfyllande heptaedrarna". Geometriae Dedicata . 7 (2): 175–184. doi : 10.1007/BF00181630 . S2CID 120562040 .
Goldberg, Michael Konvexa polyedriska rymdfyllare med mer än tolv ansikten. Geom. Dedicata 8, 491-500, 1979.
Goldberg, Michael (1981). "På den rymdfyllande oktaedran" . Geometriae Dedicata . 10 (1–4): 323–335. doi : 10.1007/BF01447431 . S2CID 189876836 .
Goldberg, Michael (1982). "På den rymdfyllande Decahedra" . {{ citera journal }} : Citera journal kräver |journal= ( hjälp )
Goldberg, Michael (1982). "På den rymdfyllande enneahedran". Geometriae Dedicata . 12 (3). doi : 10.1007/BF00147314 . S2CID 120914105 .

externa länkar

Olshevsky, George. "Honeycomb" . Ordlista för Hyperspace . Arkiverad från originalet den 4 februari 2007.
Fem rymdfyllande polyedrar , Guy Inchbald, The Mathematical Gazette 80 , november 1996, sid 466-475.
Raumfueller (Space filling polyhedra) av TE Dorozinski
Weisstein, Eric W. "Rymdfyllande polyeder" . MathWorld .

Grundläggande konvexa regelbundna och enhetliga bikakor i dimensionerna 2–9
Plats	Familj	${\tilde {A}}_{n-1}$	${\tilde {C}}_{n-1}$	${\tilde {B}}_{n-1}$	${\tilde {D}}_{n-1}$	${\tilde {G}}_{2}$ / ${\tilde {F}}_{4}$ / ${\tilde { E}}_{n-1}$
E ²	Enhetlig plattsättning	{3 ^[3] }	δ ₃	hδ ₃	qδ ₃	Hexagonal
E ³	Enhetlig konvex bikaka	{3 ^[4] }	δ ₄	hδ ₄	qδ ₄
E ⁴	Uniform 4-honeycomb	{3 ^[5] }	δ ₅	hδ ₅	qδ ₅	24-cells honungskaka
E ⁵	Uniform 5-bikaka	{3 ^[6] }	δ ₆	hδ ₆	qδ ₆
E ⁶	Uniform 6-honeycomb	{3 ^[7] }	δ ₇	hδ ₇	qδ ₇	2 ₂₂
E ⁷	Uniform 7-honeycomb	{3 ^[8] }	δ ₈	hδ ₈	qδ ₈	1 ₃₃ • 3 ₃₁
E ⁸	Uniform 8-honeycomb	{3 ^[9] }	δ ₉	hδ ₉	qδ ₉	1 ₅₂ • 2 ₅₁ • 5 ₂₁
E ⁹	Uniform 9-honeycomb	{3 ^[10] }	δ ₁₀	hδ ₁₀	qδ ₁₀
E ¹⁰	Uniform 10-honeycomb	{3 ^[11] }	δ ₁₁	hδ ₁₁	qδ ₁₁
E ^{n -1}	Uniform ( n -1)- honeycomb	{3 ^[n] }	5 _n	hδ _n	qδ _n	1 _k2 • 2 _k1 • k ₂₁