Åttakantigt kakel
| Octagonal kakel | |
|---|---|
 Poincaré skiva modell av hyperboliska planet |
|
| Typ | Hyperbolisk vanlig plattsättning |
| Vertex-konfiguration | 8 3 |
| Schläfli symbol |
{8,3} t{4,8} |
| Wythoff symbol |
3 | 8 2 2 8 | 4 4 4 4 | |
| Coxeter diagram |
|
| Symmetrigrupp |
[8,3], (*832) [8,4], (*842) [(4,4,4)], (*444) |
| Dubbel | Order-8 triangulär plattsättning |
| Egenskaper | Vertex-transitive , edge-transitive , face-transitive |
Inom geometrin är den åttkantiga plattsättningen en vanlig plattsättning av det hyperboliska planet . Den representeras av Schläfli-symbolen för {8,3} , med tre regelbundna oktagoner runt varje vertex. Den har också en konstruktion som en trunkerad order-8 kvadratisk plattsättning, t{4,8}.
Enhetliga färger
Liksom den hexagonala plattsättningen på det euklidiska planet finns det 3 enhetliga färger av denna hyperboliska plattsättning. Den dubbla plattsättningen V8.8.8 representerar de grundläggande domänerna för [(4,4,4)] symmetri.
| Regelbunden | Avkortningar | ||
|---|---|---|---|
 {8,3} |
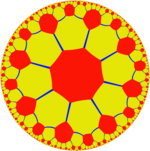 t{4,8} |
 |
|
| Dubbel plattsättning | |||
 |
 |
 |
|
Vanliga kartor
Den vanliga kartan {8,3} 2,0 kan ses som en 6-färgning av den hyperboliska plattsättningen {8,3}. Inom den vanliga kartan anses åttahörningar av samma färg vara samma ansikte som visas på flera platser. De 2,0 prenumerationerna visar att samma färg kommer att upprepas genom att flytta 2 steg i rak riktning efter motsatta kanter. Denna vanliga karta har också en representation som en dubbel täckning av en kub, representerad av Schläfli-symbolen {8/2,3}, med 6 åttakantiga ytor, dubbelt omslagna {8/2}, med 24 kanter och 16 hörn. Det beskrevs av Branko Grünbaum i hans 2003 artikel Are Your Polyhedra the Same as My Polyhedra?
Relaterade polyedrar och plattsättningar
Denna plattsättning är topologiskt en del av sekvensen av vanliga polyedrar och plattsättningar med Schläfli-symbolen {n,3}.
| * n 32 symmetrimutation av regelbundna plattsättningar: { n ,3} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sfärisk | euklidisk | Kompakt hyperb. | Paraco. | Icke-kompakt hyperbolisk | |||||||

|

|

|

|

|

|

|

|

|

|

|

|
| {2,3} | {3,3} | {4,3} | {5,3} | {6,3} | {7,3} | {8,3} | {∞,3} | {12i,3} | {9i,3} | {6i,3} | {3i,3} |
Och är också topologiskt en del av sekvensen av vanliga plattsättningar med Schläfli-symbolen {8,n}.
| Plats | Sfärisk | Kompakt hyperbolisk | Paracompact | |||||
|---|---|---|---|---|---|---|---|---|
| Kakelsättning |

|

|

|

|

|

|

|
|
| Konfig. | 8.8 | 8 3 | 8 4 | 85 | 8 6 | 87 | 8 8 | ...8∞ |
Från en Wythoff-konstruktion finns tio hyperboliska likformiga plattsättningar som kan baseras på den vanliga åttakantiga plattsättningen.
Om du ritar brickorna färgade som röda på originalytorna, gula vid de ursprungliga hörnen och blå längs originalkanterna, det finns 10 former.
| Enhetliga åttkantiga/triangulära plattor | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetri: [8,3], (*832) |
[8,3] + (832) |
[1 + ,8,3] (*443) |
[8,3 + ] (3*4) |
||||||||||
| {8,3} | t{8,3} | r{8,3} | t{3,8} | {3,8} |
rr{8,3} s 2 {3,8} |
tr{8,3} | sr{8,3} | h{8,3} | h 2 {8,3} | s{3,8} | |||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
| Uniforma dualer | |||||||||||||
| V8 3 | V3.16.16 | V3.8.3.8 | V6.6.8 | V3 8 | V3.4.8.4 | V4.6.16 | V3 4 .8 | V(3,4) 3 | V8.6.6 | V3 5 .4 | |||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
| Enhetliga åttkantiga/fyrkantiga plattsättningar | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
[8,4], (*842) (med [8,8] (*882), [(4,4,4)] (*444) , [∞,4,∞] (* 4222) index 2 subsymmetrier) (Och [(∞,4,∞,4)] (*4242) index 4 subsymmetri) |
|||||||||||
|
= = = |
= |
= = = |
= |
= = |
= |
|
|||||

|

|

|

|

|

|

|
|||||
| {8,4} |
t{8,4} |
r{8,4} | 2t{8,4}=t{4,8} | 2r{8,4}={4,8} | rr{8,4} | tr{8,4} | |||||
| Uniforma dualer | |||||||||||
|
|
|
|
|
|
|
|
|||||

|

|

|

|

|

|

|
|||||
| V8 4 | V4.16.16 | V(4,8) 2 | V8.8.8 | V4 8 | V4.4.4.8 | V4.8.16 | |||||
| Växlingar | |||||||||||
|
[1 + ,8,4] (*444) |
[8 + ,4] (8*2) |
[8,1 + ,4] (*4222) |
[8,4 + ] (4*4) |
[8,4,1 + ] (*882) |
[(8,4,2 + )] (2*42) |
[8,4] + (842) |
|||||
|
= |
= |
= |
= |
= |
= |
|
|||||

|

|

|

|

|

|

|
|||||
| h{8,4} | s{8,4} | tim{8,4} | s{4,8} | h{4,8} | hrr{8,4} | sr{8,4} | |||||
| Alternerande dualer | |||||||||||
|
|
|
|
|
|
|
|
|||||

|

|

|

|

|
|||||||
| V(4.4) 4 | V3.(3.8) 2 | V(4.4.4) 2 | V(3,4) 3 | V8 8 | V4.4 4 | V3.3.4.3.8 | |||||
| Enhetliga (4,4,4) plattsättningar | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetri: [(4,4,4)], (*444) |
[(4,4,4)] + (444) |
[(1 + ,4,4,4)] (*4242) |
[(4 + ,4,4)] (4*22) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||

|

|

|

|

|

|

|

|

|

|
||
|
0 t (4,4,4) h{8,4} |
t 0,1 (4,4,4) h 2 {8,4} |
t 1 (4,4,4) { 4,8 } 1/2 |
t 1,2 (4,4,4) h 2 {8,4} |
t 2 (4,4,4) h{8,4} |
t 0,2 (4,4,4) r {4,8 } 1/2 |
t 0,1,2 4,4,4) ( t{4,8 } 1/2 |
s(4,4,4) s { 4,8} 1/2 |
h(4,4,4) h { 4,8} 1/2 |
hr(4,4,4) hr { 4,8} 1/2 |
||
| Uniforma dualer | |||||||||||

|

|

|

|

|

|

|

|

|

|
||
| V(4.4) 4 | V4.8.4.8 | V(4.4) 4 | V4.8.4.8 | V(4.4) 4 | V4.8.4.8 | V8.8.8 | V3.4.3.4.3.4 | V8 8 | V(4,4) 3 | ||
Se även
- John H. Conway , Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Kapitel 19, The Hyperbolic Archimedean Tessellations)
- "Kapitel 10: Vanliga bikakor i hyperboliskt utrymme". Geometrins skönhet: tolv essäer . Dover Publikationer. 1999. ISBN 0-486-40919-8 . LCCN 99035678 .
externa länkar
- Weisstein, Eric W. "Hyperbolisk plattsättning" . MathWorld .
- Weisstein, Eric W. "Poincaré hyperbolisk disk" . MathWorld .
- Hyperboliskt och sfäriskt kakelgalleri
- KaleidoTile 3: Utbildningsprogramvara för att skapa sfäriska, plana och hyperboliska plattsättningar
- Hyperboliska plana tessellations, Don Hatch


