Enhetlig honungskaka
I geometri är en enhetlig bikaka eller enhetlig tessellation eller oändlig enhetlig polytop , en vertex-transitive honeycomb gjord av enhetliga polytopfasetter . Alla dess hörn är identiska och det finns samma kombination och arrangemang av ytor vid varje vertex. Dess dimension kan förtydligas som n -bikaka för en n -dimensionell bikaka.
En n -dimensionell enhetlig bikaka kan konstrueras på ytan av n -sfärer, i n -dimensionell euklidisk rymd och n -dimensionell hyperbolisk rymd . En 2-dimensionell enhetlig honungskaka kallas oftare en enhetlig plattsättning eller enhetlig tessellation.
Nästan alla enhetliga tesselleringar kan genereras av en Wythoff-konstruktion och representeras av ett Coxeter-Dynkin-diagram . Terminologin för de konvexa enhetliga polytoperna som används i enhetliga polyeder , enhetlig 4-polytop , enhetlig 5-polytop , enhetlig 6-polytop , enhetlig plattsättning och konvexa enhetliga bikakeartiklar myntades av Norman Johnson .
Wythoffian tessellations kan definieras av en vertex figur . För 2-dimensionella plattsättningar kan de ges av en vertexkonfiguration som listar sekvensen av ytor runt varje vertex. Till exempel representerar 4.4.4.4 en vanlig tessellation, en kvadratisk tegelsättning , med 4 rutor runt varje vertex. Generellt definieras en n -dimensionell enhetlig tessellation vertexfigurer av en ( n –1) -polytop med kanter märkta med heltal, som representerar antalet sidor av den polygonala ytan vid varje kant som utstrålar från vertexen.
Exempel på enhetliga honungskakor
| 2-dimensionella tesselleringar | ||||
|---|---|---|---|---|
| Sfärisk | euklidisk | Hyperbolisk | ||
| Coxeter diagram |
|
|
|
|
| Bild |
 Stympad icosidodecahedron |
 Stympad trihexagonal kakel |
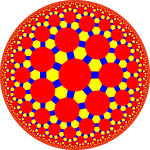 Trunkerad triheptagonal plattsättning ( Poincaré diskmodell ) |
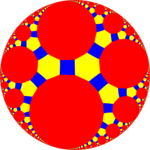 Stympad triapeirogonal plattsättning |
| Vertex figur |

|

|

|
|
| 3-dimensionella honungskakor | ||||
| 3-sfärisk | 3-Euklidiskt | 3-hyperbolisk | ||
| och paracompact enhetlig honeycomb | ||||
| Coxeter diagram |
|
|
|
|
| Bild |
 ( Stereografisk projektion ) 16-celler |
 kubisk honungskaka |
 order-4 dodekaedrisk honungskaka ( Beltrami–Klein-modell ) |
 order-4 hexagonal kakel honeycomb ( Poincaré diskmodell ) |
| Vertex figur |
 ( Oktaeder ) |
 (Oktaeder) |
 (Oktaeder) |
 (Oktaeder) |
Se även
- Enhetlig plattsättning
- Lista över enhetliga plattsättningar
- Enhetliga plattsättningar i hyperboliskt plan
- Honeycomb (geometri)
- Wythoff konstruktion
- Konvex enhetlig honungskaka
- Lista över vanliga polytoper
- George Olshevsky, Uniform Panoploid Tetracombs , Manuscript (2006) (Komplett lista med 11 konvexa enhetliga plattor, 28 konvexa enhetliga honeycombs och 143 konvexa enhetliga tetracombs)
- Branko Grünbaum , Enhetlig plattsättning av 3-utrymmen. Geombinatorics 4 (1994), 49-56.
- Norman Johnson Uniform Polytopes , Manuscript (1991)
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design . Dover Publications, Inc. ISBN 0-486-23729-X .
- Grünbaum, Branko ; Shephard, GC (1987). Kakel och mönster . WH Freeman och Company. ISBN 0-7167-1193-1 .
- HSM Coxeter , Regular Polytopes , 3rd Edition, Dover New York, 1973
- Critchlow, Keith (1970). Order in Space: A design source book . Viking Press. ISBN 0-500-34033-1 .
- NW Johnson : Theory of Uniform Polytopes and Honeycombs , Ph.D. Avhandling, University of Toronto, 1966
- A. Andreini , Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative ( Om polyedrarnas regelbundna och halvregelbundna nät och på motsvarande korrelativa nät), Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129.
externa länkar
- Weisstein, Eric W. "Uniform tessellation" . MathWorld .
- Tesselleringar av planet
- Klitzing, Richard. "2D euklidiska tesselationer" .

