5-kub

5-kub penteract (pent)
Typ	enhetlig 5-polytop
Schläfli symbol	{4,3,3,3}
Coxeter diagram
4-ansikten	10	tesseracts
Celler	40	kuber
Ansikten	80	rutor
Kanter	80
Vertices	32
Vertex figur	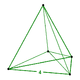5-cell
Coxeter grupp	B ₅ , [4,3 ³ ], order 3840
Dubbel	5-ortoplex
Baspunkt	(1,1,1,1,1,1)
Circumradius	sqrt(5)/2 = 1,118034
Egenskaper	konvex , isogonal regelbunden , Hanner polytop

I femdimensionell geometri är en 5-kub ett namn för en femdimensionell hyperkub med 32 hörn , 80 kanter , 80 kvadratiska ytor , 40 kubiska celler och 10 tesserakt 4-ytor .

Den representeras av Schläfli-symbolen {4,3,3,3} eller {4,3 ³ }, konstruerad som 3 tesserakter, {4,3,3}, runt varje kubisk ås . Det kan kallas en penteract , en portmanteau av det grekiska ordet pénte , för 'fem' (dimensioner), och ordet tesseract (4-kuben). Det kan också kallas en vanlig deca-5-top eller decateron , som är en 5-dimensionell polytop konstruerad av 10 vanliga fasetter .

Besläktade polytoper

Det är en del av en oändlig hyperkubfamilj . Dualen av en 5-kub är 5-ortoplexen , av den oändliga familjen av ortoplexer .

Genom att tillämpa en alterneringsoperation , ta bort alternerande hörn av 5-kuben, skapas en annan enhetlig 5-polytop , kallad en 5-demicube , som också är en del av en oändlig familj som kallas demihypercubes .

5-kuben kan ses som en order-3 tesseractic honeycomb på en 4-sfär . Det är besläktat med den euklidiska 4-mellanrums (ordning-4) tesseractic honeycomb och paracompact hyperbolic honeycomb order-5 tesseractic honeycomb .

Som en konfiguration

Denna konfigurationsmatris representerar 5-kuben. Raderna och kolumnerna motsvarar hörn, kanter, ytor, celler och 4-ytor. Diagonaltalen säger hur många av varje element som förekommer i hela 5-kuben. De icke-diagonala talen säger hur många av kolumnens element som förekommer i eller vid radens element.

$\&4&10&1045\&4\ \8&12&6&40&2\\16&32&24&8&10\end{matrix}}\end{bmatrix}}}$

kartesiska koordinater

De kartesiska koordinaterna för hörn av en 5-kub centrerad vid origo och med kantlängd 2 är

(±1,±1,±1,±1,±1),

₀ medan denna 5-kubs inre består av alla punkter ( x , x ₁ , x ₂ , x ₃ , x ₄ ) med -1 < x _i < 1 för alla i .

Bilder

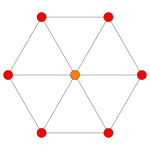
n -kub Coxeter- planprojektioner i B _k Coxeter-grupperna projicerar till k-kubgrafer, med två hörn som överlappar varandra i de projektiva graferna.

Ortografiska projektioner
Coxeter plan	B ₅	B ₄ / D ₅	B ₃ / D ₄ / A ₂
Graf
Dihedral symmetri	[10]	[8]	[6]
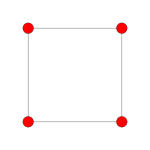
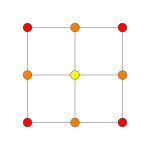
Coxeter plan	Övrig	B ₂	A ₃
Graf
Dihedral symmetri	[2]	[4]	[4]

Fler ortografiska projektioner
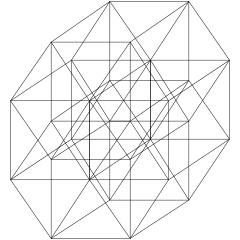Wireframe skev riktning	B5 Coxeter plan

Graf
Vertex-kantgraf.

Perspektivprojektioner
En perspektivprojektion 3D till 2D av stereografisk projektion 4D till 3D av Schlegel-diagram 5D till 4D.

Net
4D-nät av 5-kuben, perspektiv projicerat i 3D.

Utsprång

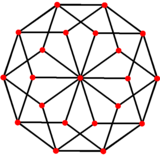
5-kuben kan projiceras ner till 3 dimensioner med ett rombiskt ikosaederhölje . Det finns 22 yttre hörn och 10 inre hörn. De 10 inre hörnen har det konvexa skrovet av en femkantig antiprisma . De 80 kanterna skjuter ut i 40 yttre kanter och 40 inre kanter. De 40 kuberna projicerar in i gyllene romboedrar som kan användas för att dissekera den rombiska ikosaedern. Projektionsvektorerna är u = {1, φ, 0, -1, φ}, v = {φ, 0, 1, φ, 0}, w = {0, 1, φ, 0, -1}, där φ är det gyllene snittet , ${\frac {1+{\sqrt {5}}}{2}}$ .

rombisk ikosaeder		5-kub
Perspektiv	ortogonal

Symmetri

5 -kuben har Coxeter-gruppsymmetri B ₅ , abstrakt struktur $C_{2}\wr S_{5}$ , order 3840, innehållande 25 hyperplan av reflektion. Schläfli- symbolen för 5-kuben, {4,3,3,3}, matchar Coxeter-notationssymmetrin [4,3,3,3].

Prismor

Alla hyperkuber har lägre symmetriformer konstruerade som prismor. 5-kuben har 7 prismatiska former från den lägsta 5- ortotopen , { } ⁵ , och uppåt eftersom ortogonala kanter är begränsade till att vara lika långa. Topparna i ett prisma är lika med produkten av hörnen i elementen. Kanterna på ett prisma kan delas upp i antalet kanter i ett element gånger antalet hörn i alla andra element.

Beskrivning	Schläfli symbol	Vertices	Kanter	Coxeter notation Symmetri	Beställa
5-kub	{4,3,3,3}	32	80	[4,3,3,3]	3840
tesseraktiskt prisma	{4,3,3}×{ }	16×2 = 32	64 + 16 = 80	[4,3,3,2]	768
kub - fyrkantig duoprism	{4,3}×{4}	8×4 = 32	48 + 32 = 80	[4,3,2,4]	384
kub- rektangel duoprism	{4,3}×{} ²	8×2 ² = 32	48 + 2×16 = 80	[4,3,2,2]	192
kvadratisk kvadratisk duoprisma prisma	{4} ² ×{ }	4 ² × 2 = 32	2×32 + 16 = 80	[4,2,4,2]	128
kvadratisk- rektangulär parallellepipedduoprism	{4}×{} ³	4×2 ³ = 32	32 + 3×16 = 80	[4,2,2,2]	64
5- ortotop	{ } ⁵	2 ⁵ = 32	5×16 = 80	[2,2,2,2]	32

Besläktade polytoper

5-kuben är 5:e i en serie av hyperkuber :

Petrie polygon ortografiska projektioner

Linjesegmentet	Fyrkant	Kub	4-kub	5-kub	6-kub	7-kub	8-kub

Den vanliga sneda polyedern {4,5| 4} kan realiseras inom 5-kuben, med dess 32 hörn, 80 kanter och 40 kvadratiska ytor, och de andra 40 kvadratiska ytorna på 5-kuben blir fyrkantiga hål .

Denna polytop är en av 31 enhetliga 5-polytoper som genereras från den vanliga 5-kuben eller 5-ortoplexen .

^ Coxeter, Regular Polytopes, avsnitt 1.8 Konfigurationer
^ Coxeter, Complex Regular Polytopes, p.117

HSM Coxeter :
- Coxeter, Regular Polytopes , (3:e upplagan, 1973), Dover-upplagan, ISBN 0-486-61480-8 , sid. 296, Tabell I (iii): Regelbundna polytoper, tre vanliga polytoper i n-dimensioner (n≥5)
- Kaleidoscopes: Selected Writings of HSM Coxeter , redigerad av F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  - (Papper 22) HSM Coxeter, Regular and Semi Regular Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  - (Papper 23) HSM Coxeter, Regular and Semi-Regular Polytopes II , [Math. Zeit. 188 (1985) 559-591]
  - (Papper 24) HSM Coxeter, Regular and Semi-Regular Polytopes III , [Math. Zeit. 200 (1988) 3-45]
Norman Johnson Uniform Polytopes , Manuscript (1991)
- NW Johnson: Theory of Uniform Polytopes and Honeycombs , Ph.D. (1966)
Klitzing, Richard. "5D enhetliga polytoper (polytera) o3o3o3o4x - pent" .

externa länkar

Weisstein, Eric W. "Hypercube" . MathWorld .
Olshevsky, George. "Mät polytop" . Ordlista för Hyperspace . Arkiverad från originalet den 4 februari 2007.
Flerdimensionell ordlista: hyperkub Garrett Jones

Grundläggande konvexa regelbundna och enhetliga polytoper i dimensionerna 2–10
Familj	A _n	B _n	I ₂ (p) / D _n	E ₆ / E ₇ / E ₈ / F ₄ / G ₂	H _n
Vanlig polygon	Triangel	Fyrkant	p-gon	Sexhörning	Pentagon
Uniform polyeder	Tetraeder	Oktaeder • Kub	Demicube		Dodekaeder • Ikosaeder
Uniform polychoron	Pentachoron	16-celler • Tesseract	Demitesseract	24-celler	120-celler • 600-celler
Uniform 5-polytop	5-simplex	5-ortoplex • 5-kub	5-demikub
Uniform 6-polytop	6-simplex	6-ortoplex • 6-kub	6-demikub	1 ₂₂ • 2 ₂₁
Uniform 7-polytop	7-simplex	7-ortoplex • 7-kub	7-demikub	1 ₃₂ • 2 ₃₁ • 3 ₂₁
Uniform 8-polytop	8-simplex	8-ortoplex • 8-kub	8-demikub	1 ₄₂ • 2 ₄₁ • 4 ₂₁
Uniform 9-polytop	9-simplex	9-ortoplex • 9-kub	9-demikub
Uniform 10-polytop	10-simplex	10-ortoplex • 10-kub	10-demikub
Uniform n - polytop	n - simplex	n - ortoplex • n - kub	n - demikub	1 _k2 • 2 _k1 • k ₂₁	n - femkantig polytop
Ämnen: Polytopfamiljer • Vanlig polytop • Lista över vanliga polytoper och sammansättningar

[1] Coxeter, Regular Polytopes, avsnitt 1.8 Konfigurationer

[2] Coxeter, Complex Regular Polytopes, p.117

B5 polytoper
β ₅	t ₁ β ₅	t ₂ γ ₅	t ₁ γ ₅	γ ₅	t _0,1 β ₅	t _0,2 β5 _{_}	t _1,2 β ₅
t _0,3 β5 _{_}	t _1,3 y ₅	t _1,2 y ₅	t _0,4 y ₅	t _0,3 y ₅	t _0,2 y ₅	t _0,1 y ₅	t _0,1,2 p5 _{_}
t _0,1,3 p5 _{_}	t _0,2,3 p5 _{_}	t _1,2,3 y ₅	t _0,1,4 p5 _{_}	t _0,2,4 y ₅	t _0,2,3 y ₅	t _0,1,4 y ₅	t _0,1,3 y ₅
t _0,1,2 y ₅	t _0,1,2,3 p5 _{_}	t _0,1,2,4 β5 _{_}	t _0,1,3,4 y ₅	t _0,1,2,4 y ₅	t _0,1,2,3 y ₅	t _0,1,2,3,4 y ₅