Lista över euklidiska uniformsplattor

Denna tabell visar de 11 konvexa enhetliga plattorna (regelbundna och halvregelbundna) på det euklidiska planet , och deras dubbla plattsättningar.
Det finns tre vanliga och åtta halvregelbundna plattor i planet. De halvregelbundna plattorna bildar nya plattor från sina dualer, var och en gjord av en typ av oregelbunden yta.
John Conway kallar dessa enhetliga dualer för katalanska plattsättningar , parallellt med de katalanska solida polyedrarna.
Enhetliga plattsättningar listas efter deras vertexkonfiguration , sekvensen av ytor som finns på varje vertex. Till exempel 4.8.8 en kvadrat och två oktagoner på en vertex.
Dessa 11 enhetliga plattor har 32 olika enhetliga färger . En enhetlig färgning gör att identiska polygoner vid en vertex kan färgas olika, samtidigt som vertexens enhetlighet och transformationskongruens mellan hörn bibehålls. (Obs: Vissa av kakelbilderna som visas nedan är inte färglika)
Utöver de 11 konvexa likformiga plattorna finns det också 14 kända icke-konvexa plattsättningar, med stjärnpolygoner och omvänd orientering vertexkonfigurationer. Ytterligare 28 enhetliga plattsättningar är kända med användning av apeirogoner . Om sicksack också tillåts finns det 23 fler kända enhetliga plattsättningar och 10 fler kända familjer beroende på en parameter: i 8 fall är parametern kontinuerlig, och i de andra 2 är den diskret. Uppsättningen är inte känd för att vara komplett.
Laves kakel
I 1987 års bok, Tilings and Patterns , kallar Branko Grünbaum de vertex-uniforma plattorna för Archimedean , parallellt med Archimedean solids . Deras dubbla plattsättningar kallas Laves tilings för att hedra kristallografen Fritz Laves . De kallas också Shubnikov–Laves plattsättningar efter Aleksei Shubnikov . John Conway kallade uniformsdualerna för katalanska plattsättningar , parallellt med de katalanska solida polyedrar.
Laves plattsättningar har hörn i mitten av de vanliga polygonerna och kanter som förbinder mitten av vanliga polygoner som delar en kant. Kakelplattorna Laves plattsättningar kallas planigoner . Detta inkluderar de 3 vanliga brickorna (triangel, kvadrat och hexagon) och 8 oregelbundna. Varje vertex har kanter jämnt fördelade runt sig. Tredimensionella analoger av planigonerna kallas stereohedron .
Dessa dubbla plattsättningar listas efter deras ansiktskonfiguration , antalet ytor vid varje vertex av ett ansikte. Till exempel V4.8.8 likbenta trianglar med ett hörn med fyra trianglar och två hörn som innehåller åtta trianglar. Orienteringarna för vertexplanigonerna (upp till D 12 ) överensstämmer med vertexdiagrammen i avsnitten nedan.
| Trianglar | Fyrhörningar | Pentagoner | Sexhörning | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
 V6 3 |
 V4.8 2 |
 V4.6.12 |
 V3.12 2 |
 V4 4 |
 V(3.6) 2 |
 V3.4.6.4 |
 V3 2 .4.3.4 |
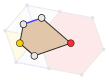 V3 4 .6 |
 V3 3 .4 2 |
 V3 6 |
Konvexa enhetliga plattsättningar av det euklidiska planet
Alla reflekterande former kan göras av Wythoff-konstruktioner , representerade av Wythoff-symboler , eller Coxeter-Dynkin-diagram , som var och en verkar på en av tre Schwarz-trianglar (4,4,2), (6,3,2) eller (3,3) ,3), med symmetri representerad av Coxeter-grupper : [4,4], [6,3] eller [3 [3] ]. Alternerade former såsom snubben kan också representeras av speciella markeringar inom varje system. Endast en enhetlig plattsättning kan inte konstrueras med en Wythoff-process, utan kan göras genom en förlängning av den triangulära plattsättningen. En ortogonal spegelkonstruktion [∞,2,∞] finns också, sedd som två uppsättningar parallella speglar som bildar en rektangulär fundamental domän. Om domänen är kvadratisk, kan denna symmetri fördubblas av en diagonal spegel till familjen [4,4].
Familjer:
-
(4,4,2), , [4,4] – Symmetri av den vanliga kvadratiska plattsättningen
- , [∞,2,∞]
- (6,3,2), , [6,3] – Symmetri av den vanliga hexagonala plattsättningen och triangulära plattsättningen .
- (3,3,3), , [3 [3] ]
Gruppfamiljen [4,4]
|
Enhetliga plattsättningar (platoniska och arkimedeiska) |
Vertexfigur och dubbel yta Wythoff-symbol(er) Symmetrigrupp Coxeterdiagram (r) |
Dubbla - enhetliga plattsättningar (kallade Laves eller katalanska plattsättningar) |
|---|---|---|
 Fyrkantig kakel (quadrille) |
  4.4.4.4 (eller 4 4 ) 4 | 2 4 p4m , [4,4], (*442) |
 självdual (quadrille) |
 Trunkerad fyrkantig kakel (stympad quadrille) |
  |
 Tetrakis fyrkantigt kakel (kisquadrille) |
 Snub fyrkantig kakel (snub quadrille) |
  |
 Kairo femkantigt kakel (4-faldig pentile) |
Gruppfamiljen [6,3]
| Platonska och arkimedeiska plattsättningar |
Vertexfigur och dubbel yta Wythoff-symbol(er) Symmetrigrupp Coxeterdiagram (r) |
Dual Laves kakel |
|---|---|---|
 Hexagonal kakel (hextile) |
  6.6.6 (eller 6 3 ) 3 | 6 2 2 6 | 3 3 3 3 | p6m , [6,3], (*632) |
 Triangulär plattsättning (deltille) |
 Trihexagonal plattsättning (hexadeltille) |
  |
 Rhombille kakel (rhombille) |
 Trunkerad hexagonal plattsättning (stympad hextile) |
  3.12.12 2 3 | 6 p6m , [6,3], (*632) |
 Triakis triangulärt kakel (kisdeltille) |
 Triangulär plattsättning (deltille) |
  |
 Hexagonal kakel (hextile) |
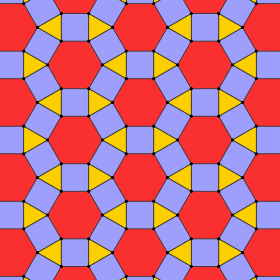 Rhombitrihexagonal plattsättning (rhombihexadeltille) |
  3.4.6.4 3 | 6 2 p6m , [6,3], (*632) |
 Deltoidal trihexagonal plattsättning (tetrille) |
 Trunkerad trihexagonal plattsättning (stympad hexadeltille) |
  4.6.12 2 6 3 | p6m , [6,3], (*632) |
 Kisrhombille plattsättning (kisrhombille) |
 Snub trihexagonal plattsättning (snub hextile) |
  3.3.3.3.6 | 6 3 2 p6 , [6,3] + , (632) |
 Floret femkantigt kakel (6-faldig pentile) |
Icke-wythoffsk enhetlig plattsättning
| Platonska och arkimedeiska plattsättningar |
Vertex figur och dubbelt ansikte Wythoff symbol(er) Symmetrigrupp Coxeter diagram |
Dual Laves kakel |
|---|---|---|
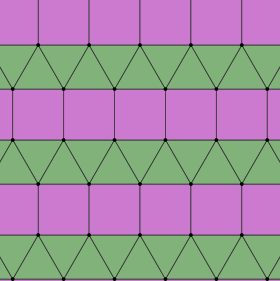 Långsträckt triangulärt kakel (isosnub quadrille) |
  3.3.3.4.4 2 | 2 (2 2) cmm , [∞,2 + ,∞], (2*22) |
 Prismatisk femkantig plattsättning (iso(4-)pentille) |
Enhetliga färger
Det finns totalt 32 enhetliga färger av de 11 enhetliga plattorna:
- Triangulär plattsättning – 9 enhetliga färger, 4 wythoffian, 5 nonwythoffian
- Fyrkantig plattsättning – 9 färger: 7 wythoffian, 2 nonwythoffian
- Hexagonal kakel – 3 färger, alla wythoffian
- Trihexagonal kakel – 2 färger, båda wythoffian
- Snub fyrkantig kakel – 2 färger, båda omväxlande wythoffian
- Stympad kvadratisk plattsättning – 2 färger, båda wythoffian
- Stympad hexagonal kakel – 1 färg, wythoffian
- Rhombitrihexagonal plattsättning – 1 färg, wythoffian
- Trunkerad trihexagonal plattsättning – 1 färg, wythoffian
- Snub hexagonal kakel – 1 färg, alternerad wythoffian
- Långsträckt triangulärt kakel – 1 färg, nonwythoffian
Se även
- Lista över tesselleringar
- Euklidiska plattsättningar av konvexa regelbundna polygoner
- Enhetliga plattsättningar i hyperboliskt plan
- Konvex enhetlig honeycomb – De 28 enhetliga 3-dimensionella tessellationerna, en parallell konstruktion till de konvexa enhetliga euklidiska plana plattorna.
- Perkolationströskel
Vidare läsning
- Conway, John H. ; Burgiel, Heidi; Goodman-Strauss, Chaim (18 april 2008). "Kapitel 19, Arkimedeiska plattsättningar , tabell 19.1". Sakernas symmetrier . AK Peters / CRC Press . ISBN 978-1-56881-220-5 . Arkiverad från originalet den 19 september 2010.
- Coxeter, HSM ; Longuet-Higgins, MS ; Miller, JCP (1954). "Uniform polyedra". Phil. Trans. 246 A: 401–450.
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design . Dover Publications, Inc. ISBN 0-486-23729-X . (Avsnitt 2–3 Cirkelpackningar, plana tesselleringar och nätverk , s. 34–40).
- Asaro, Laura; Hyde, John; Jensen, Melanie; Mann, Casey; Schroeder, Tyler. "Uniform edge -c -colorings of the Archimedean Tilings" (PDF) . University of Washington . ( Casey Mann vid University of Washington )
- Grünbaum, Branko ; Shepard, Geoffrey (november 1977). "Kapitelsättningar av vanliga polygoner" (PDF) .
- Seymour, Dale; Britton, Jill (1989). Introduktion till Tessellations . Dale Seymour Publikationer. s. 50–57, 71–74 . ISBN 978-0866514613 .





































