Hemicube (geometri)
| Hemicube | |
|---|---|
 | |
| Typ |
abstrakt regelbunden polyeder globalt projektiv polyeder |
| Ansikten | 3 rutor |
| Kanter | 6 |
| Vertices | 4 |
| Vertex-konfiguration | 4.4.4 |
| Schläfli symbol | {4,3}/2 eller {4,3} 3 |
| Symmetrigrupp | S 4 , order 24 |
| Dubbel polyeder | halvoktaeder |
| Egenskaper |
icke-orienterbar Euler-egenskap 1 |
I abstrakt geometri är en halvkub en abstrakt , regelbunden polyeder som innehåller hälften av en kubs ytor .
Insikt
Det kan realiseras som en projektiv polyeder (en tessellation av det verkliga projektiva planet med tre fyrhörningar), som kan visualiseras genom att konstruera det projektiva planet som en halvklot där motsatta punkter längs gränsen är sammankopplade och delar upp halvklotet i tre lika delar.
Den har tre fyrkantiga ytor, sex kanter och fyra hörn. Den har en oväntad egenskap att varje yta är i kontakt med varannan yta på två kanter, och varje yta innehåller alla hörn, vilket ger ett exempel på en abstrakt polytop vars ytor inte bestäms av deras vertexuppsättningar.
grafteoretisk synvinkel är skelettet en tetraedrisk graf , en inbäddning av K 4 (den kompletta grafen med fyra hörn) på ett projektivt plan .
Hemikuben ska inte förväxlas med demikuben – hemikuben är en projektiv polyeder, medan demikuben är en vanlig polyeder (i det euklidiska rymden). Medan de båda har hälften av en kubs hörn, är hemikuben en kvot av kuben, medan demikubens hörn är en delmängd av kubens hörn.
Besläktade polytoper
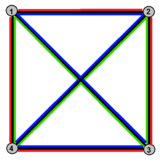
Hemikuben är Petrie-dual till den vanliga tetraedern , med de fyra hörnen, sex kanter av tetraedern och tre Petrie- polygonfyrsidiga ytor. Ansiktena kan ses som röda, gröna och blå kantfärger i den tetraedriska grafen :
Se även
Fotnoter
- McMullen, Peter ; Schulte, Egon (december 2002), "6C. Projective Regular Polytopes", Abstract Regular Polytopes (1st ed.), Cambridge University Press, s. 162–165 , ISBN 0-521-81496-0