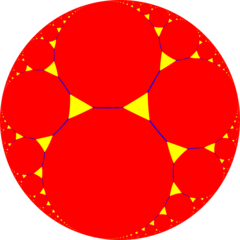
Sexkantigt kakelkaka
| Hexagonal kakel bikaka | |
|---|---|
 Perspektiv projektionsvy inom Poincaré skivmodell |
|
| Typ |
Hyperbolisk vanlig honeycomb Paracompact enhetlig honeycomb |
| Schläfli symboler |
{6,3,3} t{3,6,3} 2t{6,3,6} 2t{6,3 [3] } t{3 [3,3] } |
| Coxeter diagram |
|
| Celler |
{6,3} |
| Ansikten | hexagon {6} |
| Kantfigur | triangel {3} |
| Vertex figur |
 tetraeder {3,3} |
| Dubbel | Order-6 tetraedrisk honungskaka |
| Coxeter grupper |
, [3,3,6] , [3,6, 3] , [6,3,6] , [6 ,3 [3] ] , [3 [3,3] ] |
| Egenskaper | Regelbunden |
Inom området hyperbolisk geometri är den hexagonala bikakan med kakel en av 11 vanliga parakompakta bikakor i det 3-dimensionella hyperboliska rymden . Den är parakompakt eftersom den har celler som består av ett oändligt antal ansikten. Varje cell är en hexagonal plattsättning vars hörn ligger på en horosfär , en yta i hyperbolisk rymd som närmar sig en enda idealpunkt i oändligheten.
Schläfli -symbolen för den sexkantiga bikakan är {6,3,3}. Eftersom den för den sexkantiga plattsättningen är {6,3} har denna bikaka tre sådana sexkantiga plattsättningar som möts vid varje kant. Eftersom Schläfli-symbolen för tetraedern är {3,3}, är vertexfiguren för denna bikaka en tetraeder. Sålunda möts fyra hexagonala plattor vid varje vertex av denna bikaka, sex hexagoner möts vid varje vertex, och fyra kanter möts vid varje vertex.
Bilder
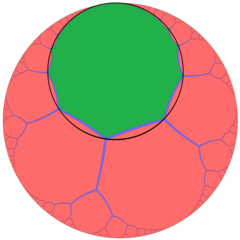
Sett i perspektiv utanför en Poincaré-skivmodell visar bilden ovan en hexagonal tegelcell inom bikakan och dess horosfär i mitten av radien (horosfären som inträffar med kantmittpunkter). I denna projektion växer hexagonerna oändligt små mot den oändliga gränsen, asymptomerande mot en enda idealpunkt. Det kan ses som liknar den apeirogonala plattsättningen av ordning 3 , {∞,3} av H 2 , med horocykler som omger hörn av apeirogonala ansikten.
| {6,3,3} | {∞,3} |
|---|---|

|
|
| En hexagonal kakelcell av den sexkantiga kakelplattan | En order-3 apeirogonal plattsättning med en grön apeirogon och dess horocykel |
Symmetrikonstruktioner
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Den har totalt fem reflekterande konstruktioner från fem relaterade Coxeter-grupper, alla med fyra speglar och endast den första är regelbunden: [6,3,3], [3,6,3], [6,3,6], [6 ,3 [3] ] och [3 [3,3] ] , med 1, 4, 6, 12 respektive 24 gånger större fundamentala domäner . I Coxeter notationsundergruppsuppmärkningar är de relaterade som: [6,(3,3) * ] (ta bort 3 speglar, index 24 undergrupp); [3,6,3 * ] eller [3 * ,6,3] (ta bort 2 speglar, index 6 undergrupp); [1 + ,6,3,6,1 + ] (ta bort två ortogonala speglar, undergrupp index 4); alla dessa är isomorfa till [3 [3,3] ]. De ringade Coxeter-diagrammen är , , , och , som representerar olika typer (färger) av hexagonala plattsättningar i Wythoff-konstruktionen .
Den har totalt fem reflekterande konstruktioner från fem relaterade Coxeter-grupper, alla med fyra speglar och endast den första är regelbunden: [6,3,3], [3,6,3], [6,3,6], [6 ,3 [3] ] och [3 [3,3] ] , med 1, 4, 6, 12 respektive 24 gånger större fundamentala domäner . I Coxeter notationsundergruppsuppmärkningar är de relaterade som: [6,(3,3) * ] (ta bort 3 speglar, index 24 undergrupp); [3,6,3 * ] eller [3 * ,6,3] (ta bort 2 speglar, index 6 undergrupp); [1 + ,6,3,6,1 + ] (ta bort två ortogonala speglar, undergrupp index 4); alla dessa är isomorfa till [3 [3,3] ]. De ringade Coxeter-diagrammen är , , , och , som representerar olika typer (färger) av hexagonala plattsättningar i Wythoff-konstruktionen .
Besläktade polytoper och bikakor
Den hexagonala bikakan är en vanlig hyperbolisk bikaka i 3-mellanrum och en av 11 som är parakompakta.
| 11 paracompact vanliga honungskakor | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 {6,3,3} |
 {6,3,4} |
 {6,3,5} |
 {6,3,6} |
 {4,4,3} |
 {4,4,4} |
||||||
 {3,3,6} |
 {4,3,6} |
 {5,3,6} |
 {3,6,3} |
 {3,4,4} |
|||||||
Det är en av 15 enhetliga parakompakta honeycombs i [6,3,3] Coxeter-gruppen, tillsammans med dess dubbla, order -6 tetraedriska honeycomb .
| [6,3,3] familjens honungskakor | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| {6,3,3} | r{6,3,3} | t{6,3,3} | rr{6,3,3} | t 0,3 {6,3,3} | tr{6,3,3} | t 0,1,3 {6,3,3} | t 0,1,2,3 {6,3,3} | ||||

|

|

|

|

|

|

|

|
||||

|

|

|

|

|

|

|
|||||
| {3,3,6} | r{3,3,6} | t{3,3,6} | rr{3,3,6} | 2t{3,3,6} | tr{3,3,6} | t 0,1,3 {3,3,6} | t 0,1,2,3 {3,3,6} | ||||
Det är en del av en sekvens av vanlig polychora , som inkluderar 5-cells {3,3,3}, tesseract {4,3,3} och 120-cell {5,3,3} av Euklidiskt 4-rum, tillsammans med andra hyperboliska bikakor som innehåller tetraedriska vertexfigurer .
| {s,3,3} bikakor | ||||||||
|---|---|---|---|---|---|---|---|---|
| Plats | S 3 | H 3 | ||||||
| Form | Ändlig | Paracompact | Icke-kompakt | |||||
| namn | {3,3,3} | {4,3,3} | {5,3,3} | {6,3,3} | {7,3,3} | {8,3,3} | ... {∞,3,3} | |
| Bild |

|

|

|

|

|

|

|
|
Coxeter diagram
|
1 |
|
|
|
|
|
|
|
| 4 |
|
|
|
|
||||
| 6 |
|
|
|
|
||||
| 12 |
|
|
|
|
||||
| 24 |
|
|
|
|
||||
|
Celler {s,3} |
 {3,3} |
 {4,3} |
 {5,3} |
 {6,3} |
 {7,3} |
 {8,3} |
 {∞,3} |
|
Det är också en del av en sekvens av vanliga bikakor av formen {6,3,p}, som var och en består av hexagonala kakelceller:
| {6,3,p} honungskakor | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Plats | H 3 | ||||||||||
| Form | Paracompact | Icke-kompakt | |||||||||
| namn | {6,3,3} | {6,3,4} | {6,3,5} | {6,3,6} | {6,3,7} | {6,3,8} | ... {6,3,∞} | ||||
| Coxeter |
|
|
|
|
|
|
|
||||
| bild |

|

|

|

|

|

|

|
||||
|
Hönsfigur {3 , p} |
{3,3} |
{3,4} |
{3,5} |
{3,6} |
{3,7} |
{3,8} |
{3,∞} |
||||
Rättad hexagonal kakel honeycomb
| Rättad hexagonal kakel honeycomb | |
|---|---|
| Typ | Paracompact enhetlig honeycomb |
| Schläfli symboler | r{6,3,3} eller t 1 {6,3,3} |
| Coxeter diagram |
|
| Celler |
|
| Ansikten |
triangel {3} sexkant {6} |
| Vertex figur |
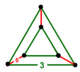 trekantsprisma |
| Coxeter grupper |
, [3,3,6] , [3,3 [ 3] ] |
| Egenskaper | Vertextransitiv, kanttransitiv |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Den rätade hexagonala bikakan , t 1 {6,3,3}, har tetraedriska och trihexagonala kakelfasetter, med en triangulär prisma vertexfigur . Den halvsymmetriska konstruktionen växlar två typer av tetraedrar.
Den rätade hexagonala bikakan , t 1 {6,3,3}, har tetraedriska och trihexagonala kakelfasetter, med en triangulär prisma vertexfigur . Den halvsymmetriska konstruktionen växlar två typer av tetraedrar.
| Sexkantigt kakelkaka |
|
|---|---|

|

|
| Relaterade H 2 plattsättningar | |
| Order-3 apeirogonal plattsättning |
|
|
 
|
Stympad hexagonal kakel bikaka
| Stympad hexagonal kakel bikaka | |
|---|---|
| Typ | Paracompact enhetlig honeycomb |
| Schläfli symbol | t{6,3,3} eller t 0,1 {6,3,3} |
| Coxeter diagram |
|
| Celler |
{3,3} t{6,3} |
| Ansikten |
triangel {3} dodecagon {12} |
| Vertex figur |
 triangulär pyramid |
| Coxeter grupper | , [3,3,6] |
| Egenskaper | Vertex-transitiv |
![]()
![]()
![]()
![]()
![]()
![]()
![]() Den avkortade hexagonala bikakan , t 0,1 {6,3,3}, har tetraedriska och stympade hexagonala kakelfasetter, med en triangulär pyramidformad vertexfigur .
Den avkortade hexagonala bikakan , t 0,1 {6,3,3}, har tetraedriska och stympade hexagonala kakelfasetter, med en triangulär pyramidformad vertexfigur .
Det liknar den 2D hyperboliska trunkerade ordningen-3 apeirogonala plattorna , t{∞,3} med apeirogonala och triangeliska ytor:
Bitruncated hexagonal kakel bikaka
|
Bitruncated hexagonal kakel honeycomb Bitruncated order-6 tetraedrisk honeycomb |
|
|---|---|
| Typ | Paracompact enhetlig honeycomb |
| Schläfli symbol | 2t{6,3,3} eller t 1,2 {6,3,3} |
| Coxeter diagram |
|
| Celler |
t{3,3} t{3,6} |
| Ansikten |
triangel {3} sexkant {6} |
| Vertex figur |
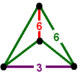 digonal disfenoid |
| Coxeter grupper |
, [3,3,6] , [3,3 [ 3] ] |
| Egenskaper | Vertex-transitiv |
![]()
![]()
![]()
![]()
![]()
![]()
![]() Den bitrunkerade hexagonala bikakan eller bitruncated order-6 tetraedrisk honeycomb , t 1,2 {6,3,3}, har trunkerade tetraeder och hexagonala plattsättningsceller , med en digonal disfenoid vertexfigur .
Den bitrunkerade hexagonala bikakan eller bitruncated order-6 tetraedrisk honeycomb , t 1,2 {6,3,3}, har trunkerade tetraeder och hexagonala plattsättningsceller , med en digonal disfenoid vertexfigur .
Kantellerad hexagonal kakel honungskaka
| Kantellerad hexagonal kakel honungskaka | |
|---|---|
| Typ | Paracompact enhetlig honeycomb |
| Schläfli symbol | rr{6,3,3} eller t 0,2 {6,3,3} |
| Coxeter diagram |
|
| Celler |
r{3,3} rr{6,3} {}×{3} |
| Ansikten |
triangel {3} kvadrat {4} sexkant {6} |
| Vertex figur |
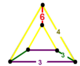 kil |
| Coxeter grupper | , [3,3,6] |
| Egenskaper | Vertex-transitiv |
![]()
![]()
![]()
![]()
![]()
![]()
![]() Den kantellerade hexagonala bikakan , t 0,2 {6,3,3}, har oktaeder , rhombitrihexagonal plattsättning och triangulära prismaceller , med en kilformad vertexfigur .
Den kantellerade hexagonala bikakan , t 0,2 {6,3,3}, har oktaeder , rhombitrihexagonal plattsättning och triangulära prismaceller , med en kilformad vertexfigur .
Cantitruncated hexagonal kakel honeycomb
| Cantitruncated hexagonal kakel honeycomb | |
|---|---|
| Typ | Paracompact enhetlig honeycomb |
| Schläfli symbol | tr{6,3,3} eller t 0,1,2 {6,3,3} |
| Coxeter diagram |
|
| Celler |
t{3,3} tr{6,3} {}×{3} |
| Ansikten |
triangel {3} kvadrat {4} hexagon {6} dodecagon {12} |
| Vertex figur |
 spegelvänd sphenoid |
| Coxeter grupper | , [3,3,6] |
| Egenskaper | Vertex-transitiv |
![]()
![]()
![]()
![]()
![]()
![]()
![]() Den vinkelräta hexagonala bikakan , t 0,1,2 {6,3,3}, har trunkerad tetraeder , trunkerad trihexagonal plattsättning och triangulära prismaceller , med en spegelvänd sphenoid vertexfigur .
Den vinkelräta hexagonala bikakan , t 0,1,2 {6,3,3}, har trunkerad tetraeder , trunkerad trihexagonal plattsättning och triangulära prismaceller , med en spegelvänd sphenoid vertexfigur .
Runcinerad hexagonal kakelkaka
| Runcinerad hexagonal kakelkaka | |
|---|---|
| Typ | Paracompact enhetlig honeycomb |
| Schläfli symbol | t 0,3 {6,3,3} |
| Coxeter diagram |
|
| Celler |
{3,3} {6,3} {}×{6} {}×{3} |
| Ansikten |
triangel {3} kvadrat {4} sexkant {6} |
| Vertex figur |
 oregelbunden triangulär antiprisma |
| Coxeter grupper | , [3,3,6] |
| Egenskaper | Vertex-transitiv |
![]()
![]()
![]()
![]()
![]()
![]()
![]() Den runcinerade hexagonala bikakan , t 0,3 {6,3,3}, har tetrahedron , hexagonal plattsättning , hexagonal prisma och triangulära prismaceller , med en oregelbunden triangulär antiprisma vertexfigur .
Den runcinerade hexagonala bikakan , t 0,3 {6,3,3}, har tetrahedron , hexagonal plattsättning , hexagonal prisma och triangulära prismaceller , med en oregelbunden triangulär antiprisma vertexfigur .
Runcitruncated hexagonal kakel bikaka
| Runcitruncated hexagonal kakel bikaka | |
|---|---|
| Typ | Paracompact enhetlig honeycomb |
| Schläfli symbol | t 0,1,3 {6,3,3} |
| Coxeter diagram |
|
| Celler |
rr{3,3} {}x{3} {}x{12} t{6,3} |
| Ansikten |
triangel {3} kvadrat {4} dodecagon {12} |
| Vertex figur |
likbent-trapesformad pyramid |
| Coxeter grupper | , [3,3,6] |
| Egenskaper | Vertex-transitiv |
![]()
![]()
![]()
![]()
![]()
![]()
![]() Den runcitruncated hexagonala plattsättningsbikakan , t 0,1,3 {6,3,3}, har cuboctahedron , triangulärt prisma , dodecagonal prisma och trunkerade hexagonala plattsättningsceller , med en likbent trapetsformad pyramidformad vertexfigur .
Den runcitruncated hexagonala plattsättningsbikakan , t 0,1,3 {6,3,3}, har cuboctahedron , triangulärt prisma , dodecagonal prisma och trunkerade hexagonala plattsättningsceller , med en likbent trapetsformad pyramidformad vertexfigur .
Runcicantellated hexagonal kakel bikaka
|
Runcicantellated hexagonal kakel honeycomb runcicantellated ordning-6 tetraedrisk honeycomb |
|
|---|---|
| Typ | Paracompact enhetlig honeycomb |
| Schläfli symbol | t 0,2,3 {6,3,3} |
| Coxeter diagram |
|
| Celler |
t{3,3} {}x{6} rr{6,3} |
| Ansikten |
triangel {3} kvadrat {4} sexkant {6} |
| Vertex figur |
 likbent-trapesformad pyramid |
| Coxeter grupper | , [3,3,6] |
| Egenskaper | Vertex-transitiv |
![]()
![]()
![]()
![]()
![]()
![]()
![]() Den runcikantellerade hexagonala kakelbikakan eller runcitruncated order-6 tetraedriska honeycomb , t 0,2,3 {6,3,3}, har trunkerade tetrahedron , hexagonala prisma och rombitrihexagonala plattsättningsceller , med en likbent pyramidformad figur .
Den runcikantellerade hexagonala kakelbikakan eller runcitruncated order-6 tetraedriska honeycomb , t 0,2,3 {6,3,3}, har trunkerade tetrahedron , hexagonala prisma och rombitrihexagonala plattsättningsceller , med en likbent pyramidformad figur .
Omnitruncated hexagonal kakel bikaka
|
Omnitruncated hexagonal kakel honeycomb Omnitruncated order-6 tetraedrisk honeycomb |
|
|---|---|
| Typ | Paracompact enhetlig honeycomb |
| Schläfli symbol | t 0,1,2,3 {6,3,3} |
| Coxeter diagram |
|
| Celler |
tr{3,3} {}x{6} {}x{12} tr{6,3} |
| Ansikten |
fyrkantig {4} hexagon {6} dodecagon {12} |
| Vertex figur |
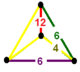 oregelbunden tetraeder |
| Coxeter grupper | , [3,3,6] |
| Egenskaper | Vertex-transitiv |
![]()
![]()
![]()
![]()
![]()
![]()
![]() Den omnitrunkerade hexagonala bikakan eller omnitruncated order-6 tetraedrisk honeycomb , t 0,1,2,3 {6,3,3}, har trunkerad oktaeder , hexagonal prisma , tvåsidigt prisma och trunkerad trihexagonal tetraedrisk regelbunden cell , figur .
Den omnitrunkerade hexagonala bikakan eller omnitruncated order-6 tetraedrisk honeycomb , t 0,1,2,3 {6,3,3}, har trunkerad oktaeder , hexagonal prisma , tvåsidigt prisma och trunkerad trihexagonal tetraedrisk regelbunden cell , figur .
Se även
- Konvexa enhetliga bikakor i hyperboliskt utrymme
- Regelbundna tesselleringar av hyperboliskt 3-mellanslag
- Paracompact enhetliga honungskakor
- Alternerad hexagonal kakel honeycomb
- Coxeter , Regular Polytopes , 3:a. ed., Dover Publications, 1973. ISBN 0-486-61480-8 . (Tabell I och II: Vanliga polytoper och honeycombs, s. 294–296)
- The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN 99-35678 , ISBN 0-486-40919-8 (Kapitel 10, Regular Honeycombs in Hyperbolic Space Archived 2016-06-10 at the Wayback III Machine ) T
- Jeffrey R. Weeks The Shape of Space, 2:a upplagan ISBN 0-8247-0709-5 (Kapitel 16–17: Geometries on Three-manifolds I,II)
- NW Johnson, R. Kellerhals , JG Ratcliffe, ST Tschantz, The size of a hyperbolic Coxeter simplex , Transformation Groups (1999), Volym 4, Issue 4, s 329–353 [ 1] [2]
- NW Johnson, R. Kellerhals , JG Ratcliffe, ST Tschantz, Commensurability classes of hyperbolic Coxeter groups , (2002) H 3 : p130. [3]
externa länkar
- John Baez , Visual Insight : {6,3,3} Honeycomb (2014/03/15)
- John Baez , Visual Insight : {6,3,3} Honeycomb in Upper Half Space (2013/09/15)
- John Baez , Visual Insight : Truncated {6,3,3} Honeycomb (2016/12/01)