Vanligt rutnät
Ett regelbundet rutnät är en tessellation av n -dimensionell euklidisk rymd av kongruenta parallellotoper (t.ex. tegelstenar ). Dess motsats är oregelbundet rutnät .
Rutnät av denna typ visas på grafpapper och kan användas i finita elementanalys , finita volymmetoder , finita differensmetoder och i allmänhet för diskretisering av parameterutrymmen. Eftersom derivatorna av fältvariabler bekvämt kan uttryckas som ändliga skillnader, uppträder strukturerade rutnät huvudsakligen i ändliga differensmetoder. Ostrukturerade rutnät erbjuder mer flexibilitet än strukturerade rutnät och är därför mycket användbara i metoder med finita element och finita volymer.
Varje cell i rutnätet kan adresseras med index (i, j) i två dimensioner eller (i, j, k) i tre dimensioner, och varje vertex har koordinater i 2D eller i 3D för några reella tal dx , dy och dz som representerar rutnätsavståndet.
Relaterade rutnät
Ett kartesiskt rutnät är ett specialfall där elementen är enhetskvadrater eller enhetskuber , och hörnen är punkter på heltalsgittret .
Ett rätlinjigt rutnät är en tessellation av rektanglar eller rektangulära kuboider (även kända som rektangulära parallellepipeder ) som i allmänhet inte är kongruenta med varandra. Cellerna kan fortfarande indexeras med heltal enligt ovan, men mappningen från index till vertexkoordinater är mindre enhetlig än i ett vanligt rutnät. Ett exempel på ett rätlinjigt rutnät som inte är regelbundet visas på grafiskt papper i logaritmisk skala .
Ett skevt rutnät är en tessellation av parallellogram eller parallellepipeder . (Om enhetslängderna alla är lika, är det en tessellation av rhombi eller rhombohedra .)
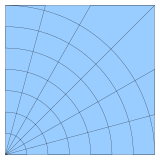
Ett kurvlinjärt rutnät eller strukturerat rutnät är ett rutnät med samma kombinatoriska struktur som ett vanligt rutnät, där cellerna är fyrhörningar eller [allmänna] kuboider , snarare än rektanglar eller rektangulära kuboider.
3-D kartesiskt rutnät
3D rätlinjigt rutnät
2-D krökt rutnät
Icke-krökt kombination av olika 2-D kurvlinjära rutnät
2-D triangulärt rutnät.
Se även
- Kartesiskt koordinatsystem – Det vanligaste koordinatsystemet (geometri)
- Heltalsgitter – Gittergrupp i det euklidiska rymden vars punkter är heltals n-tupler
- Ostrukturerat rutnät – Ostrukturerat (eller oregelbundet) rutnät är en tessellation av en del av det euklidiska planet
- Diskretisering – Process för att överföra kontinuerliga funktioner till diskreta motsvarigheter
