9-ortoplex

Vanlig 9-ortoplex Ennecross
Ortogonal projektion inuti Petrie polygon
Typ	Vanlig 9-polytop
Familj	ortoplex
Schläfli symbol	{3 7 ,4} {3 6 ,3 1,1 }
Coxeter-Dynkin diagram
8-ansikten	512 {3 7 }
7-ansikten	2304 {3 6 }
6-ansikten	4608 {3 5 }
5-ansikten	5376 {3 4 }
4-ansikten	4032 {3 3 }
Celler	2016 {3,3}
Ansikten	672 {3}
Kanter	144
Vertices	18
Vertex figur	Octacross
Petrie polygon	Octadecagon
Coxeter grupper	C 9 , [3 7 ,4] D 9 , [3 6,1,1 ]
Dubbel	9-kub
Egenskaper	konvex , Hanner polytop

I geometri är en 9-ortoplex eller 9- korspolytop en vanlig 9-polytop med 18 hörn , 144 kanter , 672 triangelytor , 2016 tetraederceller , 4032 5-celler 4-ytor , 5376 5- faces, 5376 5-faces 4608 6-simplex 6-faces , 2304 7-simplex 7-faces och 512 8-simplex 8-faces .

Den har två konstruerade former, den första är regelbunden med Schläfli-symbolen {3 ^7,4 } och den andra med växelvis märkta (rutiga) fasetter, med Schläfli-symbolen {3 ⁶ ,3 ^1,1 } eller Coxeter-symbolen 6 ₁₁ .

Det är en av en oändlig familj av polytoper, kallade korspolytoper eller ortoplexer . Den dubbla polytopen är 9- hyperkuben eller enneract .

Alternativa namn

• Enneacross , härlett från att kombinera familjenamnet korspolytop med ennea för nio (dimensioner) på grekiska
• Pentacosidodecayotton som en 512- facetterad 9-polytop (polyyotton)

Konstruktion

Det finns två Coxeter-grupper associerade med 9-ortoplexet, en vanlig , dual av enneract med C _9- eller [4,3 ⁷ ]-symmetrigruppen, och en lägre symmetri med två kopior av 8-simplexa fasetter, alternerande, med D ₉ eller [3 ^6,1,1 ] symmetrigrupp.

kartesiska koordinater

Kartesiska koordinater för hörn av en 9-ortoplex, centrerad vid origo, är

(±1,0,0,0,0,0,0,0,0), (0,±1,0,0,0,0,0,0,0), (0,0,±1, 0,0,0,0,0,0), (0,0,0,±1,0,0,0,0,0), (0,0,0,0,±1,0,0, 0,0), (0,0,0,0,0,±1,0,0,0), (0,0,0,0,0,0,±1,0,0), (0, 0,0,0,0,0,0,±1,0), (0,0,0,0,0,0,0,0,±1)

Varje vertexpar är förbundna med en kant , utom motsatser.

Bilder

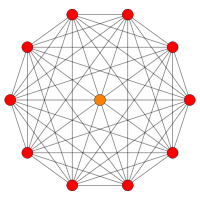
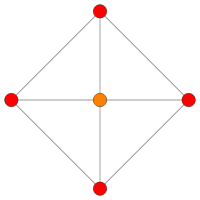
ortografiska projektioner

B 9		B 8		B 7
[18]		[16]		[14]
B 6			B 5
[12]			[10]
B 4		B 3		B 2
[8]		[6]		[4]
En 7		En 5		A 3
—		—		—
[8]		[6]		[4]

• HSM Coxeter :
  • HSM Coxeter, Regular Polytopes , 3:e upplagan, Dover New York, 1973
  •   Kaleidoscopes: Selected Writings of HSM Coxeter , redigerad av F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
    • (Papper 22) HSM Coxeter, Regular and Semi Regular Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Papper 23) HSM Coxeter, Regular and Semi-Regular Polytopes II , [Math. Zeit. 188 (1985) 559-591]
    • (Papper 24) HSM Coxeter, Regular and Semi-Regular Polytopes III , [Math. Zeit. 200 (1988) 3-45]
• Norman Johnson Uniform Polytopes , Manuscript (1991)
  • NW Johnson: Theory of Uniform Polytopes and Honeycombs , Ph.D.
• Klitzing, Richard. "9D enhetliga polytoper (polyyotta) x3o3o3o3o3o3o3o4o - vee" .

externa länkar

• Olshevsky, George. "Cross polytope" . Ordlista för Hyperspace . Arkiverad från originalet den 4 februari 2007.
• Polytoper av olika dimensioner
• Flerdimensionell ordlista