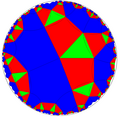
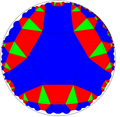
Kvartalsbeställning-6 fyrkantiga plattor
| Kvartalsordning-6 kvadratisk kakel | |
|---|---|
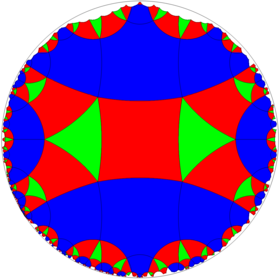 Poincaré-skivmodell av hyperbolplanet |
|
| Typ | Hyperbolisk enhetlig plattsättning |
| Vertex figur | 3.4.6.6.4 |
| Schläfli symbol | q{4,6} |
| Coxeter diagram |
|
| Dubbel | ? |
| Egenskaper | Vertex-transitiv |
Inom geometri är kvartsordningen -6 kvadratiska plattsättning en enhetlig plattsättning av det hyperboliska planet . Den har Schläfli-symbolen q{4,6}. Den är konstruerad från *3232 orbifold notation , och kan ses som en halvsymmetri av *443 och *662, och kvartssymmetri av *642.
Bilder
Projektioner centrerade på en vertex, triangel och hexagon:
Relaterade polyedrar och plattsättning
| Liknande H2 plattsättningar i *3232 symmetri | ||||||||
|---|---|---|---|---|---|---|---|---|
|
Coxeter diagram |
|
|
|
|
||||
|
|
|
|
|
|||||
|
|
|
|
|
|||||
|
Vertex figur |
6 6 | (3.4.3.4) 2 | 3.4.6.6.4 | 6.4.6.4 | ||||
| Dubbel |

|

|
||||||
| bild |

|

|

|

|
||||
| Enhetliga (4,4,3) plattsättningar | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Symmetri: [(4,4,3)] (*443) |
[(4,4,3)] + (443) |
[(4,4,3 + )] (3*22) |
[(4,1 + ,4,3)] (*3232) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|

|

|

|

|

|

|

|

|

|

|
|
0 h{6,4} t (4,4,3) |
h 2 {6,4} t 0,1 (4,4,3) |
{ 4,6} 1/2 ) t 1 (4,4,3 |
h 2 {6,4} t 1,2 (4,4,3) |
h{6,4} t 2 (4,4,3) |
r{6,4} 1/2 4,4,3 ) t 0,2 ( |
t{4,6} 1 / 2 t 0,1,2 (4,4,3) |
) s{4,6} 1/2 s (4,4,3 |
tim{4,6}1/2 tim(4,3,4) |
) h{4,6} 1/2 h (4,3,4 |
q{4,6} h 1 (4,3,4) |
| Uniforma dualer | ||||||||||

|

|

|

|
|||||||
| V(3.4) 4 | V3.8.4.8 | V(4.4) 3 | V3.8.4.8 | V(3.4) 4 | V4.6.4.6 | V6.8.8 | V3.3.3.4.3.4 | V(4.4.3) 2 | V6 6 | V4.3.4.6.6 |
Se även
- Fyrkantig kakel
- Plattläggning av vanliga polygoner
- Lista över enhetliga plana plattor
- Lista över vanliga polytoper
- John H. Conway , Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Kapitel 19, The Hyperbolic Archimedean Tessellations)
- "Kapitel 10: Vanliga bikakor i hyperboliskt utrymme". Geometrins skönhet: tolv essäer . Dover Publikationer. 1999. ISBN 0-486-40919-8 . LCCN 99035678 .
externa länkar
- Weisstein, Eric W. "Hyperbolisk plattsättning" . MathWorld .
- Weisstein, Eric W. "Poincaré hyperbolisk disk" . MathWorld .
- Hyperboliskt och sfäriskt kakelgalleri
- KaleidoTile 3: Utbildningsprogramvara för att skapa sfäriska, plana och hyperboliska plattsättningar
- Hyperboliska plana tessellations, Don Hatch