Trunkerad order-8 triangulär plattsättning

Trunkerad order-8 triangulär kakel
Poincaré-skivmodell av hyperbolplanet
Typ	Hyperbolisk enhetlig plattsättning
Vertex-konfiguration	8.6.6
Schläfli symbol	t{3,8}
Wythoff symbol	2 8 | 3 4 3 3 |
Coxeter diagram
Symmetrigrupp	[8,3], (*832) [(4,3,3)], (*433)
Dubbel	Octakis åttkantigt kakel
Egenskaper	Vertex-transitiv

I geometri är den trunkerade ordningen-8 triangulära plattsättningen en halvregelbunden plattsättning av det hyperboliska planet. Det finns två hexagoner och en oktagon på varje vertex . Den har Schläfli-symbolen för t{3,8}.

Enhetliga färger

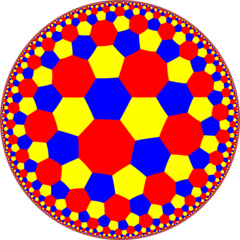Halvsymmetrin [1 + ,8,3] = [(4,3,3)] kan visas med omväxlande två hexagonfärger

Dubbel plattsättning

Symmetri

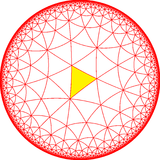
Dual av denna sida representerar de grundläggande domänerna av *443 symmetri. Den har bara en undergrupp 443, som ersätter speglar med rotationspunkter.

Denna symmetri kan fördubblas till 832 symmetri genom att lägga till en halvskärande spegel till den fundamentala domänen.

Små indexundergrupper av [(4,3,3)], (*433)

Typ	Reflekterande	Roterande
Index	1	2
Diagram
Coxeter ( orbifold )	[(4,3,3)] = (*433)	[(4,3,3)] + = (433)

Relaterade plattsättningar

Från en Wythoff-konstruktion finns tio hyperboliska likformiga plattsättningar som kan baseras på den vanliga åttakantiga plattsättningen.

Enhetliga åttkantiga/triangulära plattor
Symmetri: [8,3], (*832)							[8,3] + (832)	[1 + ,8,3] (*443)		[8,3 + ] (3*4)
{8,3}	t{8,3}	r{8,3}	t{3,8}	{3,8}	rr{8,3} s 2 {3,8}	tr{8,3}	sr{8,3}	h{8,3}	h 2 {8,3}	s{3,8}
								eller	eller
Uniforma dualer
V8 3	V3.16.16	V3.8.3.8	V6.6.8	V3 8	V3.4.8.4	V4.6.16	V3 4 .8	V(3,4) 3	V8.6.6	V3 5 .4

Den kan också genereras från (4 3 3) hyperboliska plattsättningar:

Enhetliga (4,3,3) plattsättningar
Symmetri: [(4,3,3)], (*433)							[(4,3,3)] + , (433)
0 h{8,3} t (4,3,3)	r{3,8} 1/2 4,3,3 ) t 0,1 (	h{8,3} t 1 (4,3,3)	h 2 {8,3} t 1,2 (4,3,3)	) {3,8} 1/2 t 2 ( 4,3,3	h 2 {8,3} t 0,2 (4,3,3)	t{3,8} 1 / 2 t 0,1,2 (4,3,3)	) s{3,8} 1/2 s (4,3,3
Uniforma dualer
V(3,4) 3	V3.8.3.8	V(3,4) 3	V3.6.4.6	V(3.3) 4	V3.6.4.6	V6.6.8	V3.3.3.3.3.4

Denna hyperboliska plattsättning är topologiskt relaterad som en del av sekvensen av enhetliga trunkerade polyedrar med vertexkonfigurationer (n.6.6) och [n,3] Coxeter-gruppsymmetri .

* n 32 symmetrimutation av trunkerade plattsättningar: n .6.6
Sym. * n 42 [n,3]	Sfärisk				Euklid.	Kompakt		Parac.	Icke-kompakt hyperbolisk
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
Stympade figurer
Konfig.	2.6.6	3.6.6	4.6.6	5.6.6	6.6.6	7.6.6	8.6.6	∞.6.6	12i.6.6	9i.6.6	6i.6.6
n-kis figurer
Konfig.	V2.6.6	V3.6.6	V4.6.6	V5.6.6	V6.6.6	V7.6.6	V8.6.6	V∞.6.6	V12i.6.6	V9i.6.6	V6i.6.6

* n 32 symmetrimutation av omnitrunkerade plattsättningar: 6.8.2n
Sym. * n 43 [( n ,4,3)]	Sfärisk	Kompakt hyperbolisk						Paraco.
	*243 [4,3]	*343 [(3,4,3)]	*443 [(4,4,3)]	*543 [(5,4,3)]	*643 [(6,4,3)]	*743 [(7,4,3)]	*843 [(8,4,3)]	*∞43 [(∞,4,3)]
Siffror
Konfig.	4.8.6	6.8.6	8.8.6	10.8.6	12.8.6	14.8.6	16.8.6	∞.8.6
Dualer
Konfig.	V4.8.6	V6.8.6	V8.8.6	V10.8.6	V12.8.6	V14.8.6	V16.8.6	V6.8.∞

Se även

• Triangulär kakel
• Order-3 åttkantiga plattor
• Order-8 triangulär plattsättning
• Plattläggning av vanliga polygoner
• Lista över enhetliga plattsättningar

•   John H. Conway , Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Kapitel 19, The Hyperbolic Archimedean Tessellations)
•    "Kapitel 10: Vanliga bikakor i hyperboliskt utrymme". Geometrins skönhet: tolv essäer . Dover Publikationer. 1999. ISBN 0-486-40919-8 . LCCN 99035678 .

externa länkar

• Weisstein, Eric W. "Hyperbolisk plattsättning" . MathWorld .
• Weisstein, Eric W. "Poincaré hyperbolisk disk" . MathWorld .
• Hyperboliskt och sfäriskt kakelgalleri
• KaleidoTile 3: Utbildningsprogramvara för att skapa sfäriska, plana och hyperboliska plattsättningar
• Hyperboliska plana tessellations, Don Hatch