Vertex-konfiguration

Icosidodecahedron	Vertexfigur representerad som $3.5.3.5$ eller $(3.5) 2$

Inom geometri är en vertexkonfiguration en förkortning för att representera vertexfiguren av en polyeder eller plattsättning som sekvensen av ansikten runt en vertex . För enhetliga polyedrar finns det bara en vertextyp och därför definierar vertexkonfigurationen polyedern helt. ( Chirala polyedrar finns i spegelbildspar med samma vertexkonfiguration.)

En vertexkonfiguration ges som en sekvens av tal som representerar antalet sidor på ytorna som går runt vertexet. Notationen " $abc$ " beskriver en vertex som har 3 ytor runt sig, ytor med $a$ , $b$ , och $c$ -sidor.

Till exempel, " $3.5.3.5$ " indikerar en vertex som tillhör 4 ytor, alternerande trianglar och femhörningar . Denna vertexkonfiguration definierar den vertextransitiva icosidodecahedronen . Notationen är cyklisk och är därför likvärdig med olika utgångspunkter, så $3.5.3.5$ är detsamma som $5.3.5.3.$ Ordningen är viktig, så $3.3.5.5$ skiljer sig från $3.5.3.5$ (den första har två trianglar följt av två femhörningar). Upprepade element kan samlas in som exponenter så detta exempel representeras också som $(3.5) 2$ .

Det har på olika sätt kallats en vertexbeskrivning , vertextyp , vertexsymbol , vertexarrangemang , vertexmönster , ansiktsvektor . Det kallas också en Cundy och Rollett symbol för dess användning för arkimedeiska fasta ämnen i deras 1952 bok Mathematical Models .

Vertex figurer

En vertexkonfiguration kan också representeras som en polygonal vertexfigur som visar ytorna runt vertexen. Denna vertexfigur har en 3-dimensionell struktur eftersom ytorna inte är i samma plan för polyedrar, men för vertexuniforma polyedrar är alla närliggande hörn i samma plan och därför kan denna planprojektion användas för att visuellt representera vertexkonfigurationen .

Variationer och användningsområden

Reguljära vertexfigurnät, { p , q } = *p ^q*
{3,3} = 3 ³ Defekt 180°	{3,4} = 3 ⁴ Defekt 120°	{3,5} = 3 ⁵ Defekt 60°	{3,6} = 3 ⁶ Defekt 0°
{4,3} Defekt 90°	{4,4} = 4 ⁴ Defekt 0°	{5,3} = 5 ³ Defekt 36°	{6,3} = 6 ³ Defekt 0°
En vertex behöver minst 3 ytor och en vinkeldefekt . En 0° vinkeldefekt kommer att fylla det euklidiska planet med en vanlig plattsättning. Enligt Descartes teorem är antalet hörn 720°/ defekt (4π radianer/ defekt ).

Olika beteckningar används, ibland med kommatecken (,) och ibland punktavgränsare (.). Periodoperatorn är användbar eftersom den ser ut som en produkt och en exponentnotation kan användas. Till exempel skrivs 3.5.3.5 ibland som (3.5) ² .

Notationen kan också betraktas som en expansiv form av den enkla Schläfli-symbolen för vanliga polyedrar . Schläfli-notationen { p , q } betyder q p -goner runt varje vertex. Så { p , q } kan skrivas som ppp.. ( q gånger) eller p ^q . Till exempel är en ikosaeder {3,5} = 3.3.3.3.3 eller 3 ⁵ .

Denna notation gäller för polygonala plattsättningar såväl som polyedrar. En plan vertexkonfiguration betecknar en enhetlig plattsättning precis som en icke-planar vertexkonfiguration betecknar en enhetlig polyeder.

Notationen är tvetydig för kirala former. Till exempel snubbningskuben medurs och moturs former som är identiska över spegelbilder. Båda har en 3.3.3.3.4 vertexkonfiguration.

Stjärnpolygoner

Notationen gäller även för icke-konvexa regelbundna ytor, stjärnpolygonerna . Till exempel har ett pentagram symbolen {5/2}, vilket betyder att det har 5 sidor som går runt mitten två gånger.

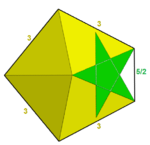
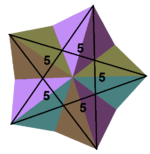
Till exempel finns det 4 vanliga stjärnpolyedrar med reguljära polygon eller stjärnpolygon vertexfigurer. Den lilla stjärnformade dodekaedern har Schläfli-symbolen {5/2,5} som expanderar till en explicit vertexkonfiguration 5/2.5/2.5/2.5/2.5/2 eller kombinerad som (5/2) ⁵ . Den stora stjärnformade dodekaedern , {5/2,3} har en triangulär vertexfigur och konfiguration (5/2.5/2.5/2) eller (5/2) ³ . Den stora dodekaedern , {5,5/2} har en pentagrammisk vertexfigur, med vertexkonfigurationen är (5.5.5.5.5)/2 eller (5 ⁵ )/2. En stor ikosaeder , {3,5/2} har också en pentagrammisk vertexfigur, med vertexkonfiguration (3.3.3.3.3)/2 eller (3 ⁵ )/2.

{5/2,5} = (5/2) ⁵	{5/2,3} = (5/2) ³	3 ⁴ .5/2	3 ⁴ .5/3	(3 ⁴ .5/2)/2


{5,5/2} = (5 ⁵ )/2	{3,5/2} = (3 ⁵ )/2	V.3 ^{4 ,} 5/2	V3 ⁴ .5/3	V(3 ⁴ .5/2)/2

Inverterade polygoner

Ansikten på en vertexfigur anses gå i en riktning. Vissa enhetliga polyedrar har vertexfigurer med inversioner där ansiktena fortskrider retrograd. En vertexfigur representerar detta i stjärnpolygonnotationen för sidorna p/q så att p <2 q , där p är antalet sidor och q antalet varv runt en cirkel. Till exempel betyder "3/2" en triangel som har hörn som går runt två gånger, vilket är samma sak som bakåt en gång. På samma sätt är "5/3" ett baklänges pentagram 5/2.

Alla enhetliga vertexkonfigurationer av regelbundna konvexa polygoner

Halvregelbundna polyedrar har vertexkonfigurationer med positiv vinkeldefekt .

OBS: Hönsfiguren kan representera en regelbunden eller halvregelbunden plattsättning på planet om dess defekt är noll. Det kan representera en plattsättning av det hyperboliska planet om dess defekt är negativ.

För enhetliga polyedrar kan vinkeldefekten användas för att beräkna antalet hörn. Descartes sats säger att alla vinkeldefekter i en topologisk sfär måste summeras till 4 π radianer eller 720 grader.

Eftersom enhetliga polyedrar har alla identiska hörn, tillåter denna relation oss att beräkna antalet hörn, vilket är 4 π / defekt eller 720 / defekt .

Exempel: En trunkerad kub 3.8.8 har en vinkeldefekt på 30 grader. Därför har den $720/30 = 24$ hörn.

I synnerhet följer att { a , b } har $4 / (2 - b (1 - 2/ a))$ hörn.

Varje uppräknad vertexkonfiguration definierar potentiellt unikt en halvregelbunden polyeder. Men alla konfigurationer är inte möjliga.

Topologiska krav begränsar existensen. Specifikt pqr att en p -gon är omgiven av alternerande q -goner och r -goner, så antingen är p jämnt eller q är lika med r . På samma sätt q jämnt eller p lika med r , och r är jämnt eller p lika med q . Därför är potentiellt möjliga trippel 3.3.3, 3.4.4, 3.6.6, 3.8.8, 3.10.10, 3.12.12, 4.4. n (för valfritt n >2), 4.6.6, 4.6.8, 4.6.10, 4.6.12, 4.8.8, 5.5.5, 5.6.6, 6.6.6. Faktum är att alla dessa konfigurationer med tre ansikten som möts vid varje vertex visar sig existera.

Antalet inom parentes är antalet hörn, bestämt av vinkeldefekten.

Trippel

Platoniska fasta ämnen 3.3.3 (4), 4.4.4 (8), 5.5.5 (20)
prismor 3.4.4 (6), 4.4.4 (8; även listade ovan), 4.4. n (2 n )
Arkimedeiska fasta ämnen 3.6.6 (12), 3.8.8 ( 24), 3.10.10 (60), 4.6.6 (24), 4.6.8 (48), 4.6.10 (120), 5.6.6 (60) .
vanlig plattsättning 6.6.6
halvregelbundna plattsättningar 3.12.12 , 4.6.12 , 4.8.8

Fyrdubblar

Platonsk solid 3.3.3.3 (6)
antiprismor 3.3.3.3 (6; även listad ovan), 3.3.3. n (2 n )
Arkimedeiska fasta ämnen 3.4.3.4 (12), 3.5.3.5 (30), 3.4.4.4 (24), 3.4.5.4 (60)
vanlig plattsättning 4.4.4.4
halvregelbundna plattsättningar 3.6.3.6 , 3.4.6.4

Femdubblar

Platonsk solid 3.3.3.3.3 (12)
Arkimedeiska fasta ämnen 3.3.3.3.4 (24), 3.3.3.3.5 (60) (båda kirala )
halvregelbundna plattsättningar 3.3.3.3.6 (kiral), 3.3.3.4.4 , 3.3.4.3.4 (observera att de två olika ordningsföljderna av samma nummer ger två olika mönster)

Sextuplar

vanlig plattsättning 3.3.3.3.3.3

Ansiktskonfiguration

Rombisk dodekaeder

De likformiga dubbla eller katalanska fasta ämnena , inklusive bipyramiderna och trapezoedrarna , är vertikalt-regelbundna ( ansiktsövergående ) och så kan de identifieras med en liknande notation som ibland kallas ansiktskonfiguration . Cundy och Rollett gav dessa dubbla symboler prefixet med ett V . Tillings and Patterns däremot använder hakparenteser runt symbolen för isoedriska plattsättningar.

Denna notation representerar en sekventiell räkning av antalet ansikten som finns vid varje vertex runt ett ansikte . Till exempel representerar V3.4.3.4 eller V(3.4) ^{2 den} rombiska dodekaedern som är ansiktstransitiv: varje ansikte är en romb och omväxlande hörn på romben innehåller 3 eller 4 ansikten vardera.

Anteckningar

Cundy, H. och Rollett, A., Mathematical Models (1952), (3:e upplagan, 1989, Stradbroke, England: Tarquin Pub.), 3.7 The Archimedean Polyhedra . pp. 101–115, s. 118–119 Tabell I, Nets of Archimedean Duals, V. a . b . c ... som vertikalt regelbundna symboler.
Peter Cromwell, Polyhedra , Cambridge University Press (1977) The Archimedean solids. pp. 156–167.
Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design . Dover Publications, Inc. ISBN 0-486-23729-X . Använder Cundy-Rollett-symbolen.
Grünbaum, Branko ; Shephard, GC (1987). Kakel och mönster . WH Freeman och Company. ISBN 0-7167-1193-1 . pp. 58–64, Tilings of regular polygons abc... (Tilings by regular polygons and star polygons) s. 95–97, 176, 283, 614–620, Monohedral plattsättningssymbol [v ₁ .v ₂ . ... .v _r ]. s. 632–642 ihåliga plattsättningar.
The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 (s. 289 Vertex-figurer, använder kommaseparator, för arkimediska fasta ämnen och plattsättningar).

externa länkar

Consistent Vertex Descriptions Stella (mjukvara) , Robert Webb