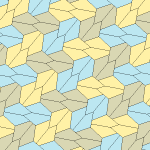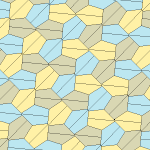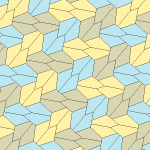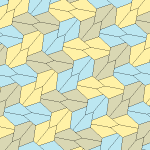
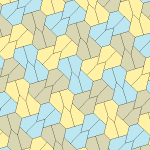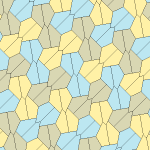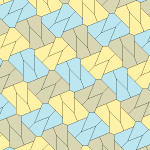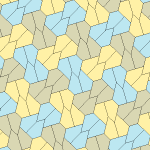
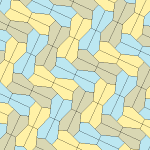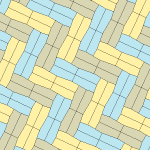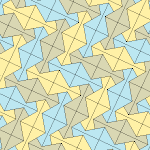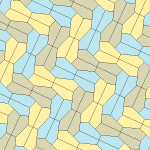
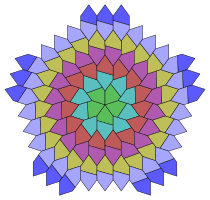
Femkantigt kakel

Den 15:e monoedriska konvexa femkantiga typen , upptäckt 2015

Inom geometrin är en femkantig plattsättning en plattsättning av planet där varje enskild del har formen av en femhörning .

En regelbunden femkantig plattsättning på det euklidiska planet är omöjlig eftersom den inre vinkeln för en regelbunden femhörning , 108°, inte är en divisor på 360°, vinkelmåttet för ett helt varv . Emellertid kan regelbundna femhörningar belägga det hyperboliska planet med fyra femhörningar runt varje vertex ( eller fler ) och sfär med tre femhörningar ; den senare producerar en beläggning topologiskt likvärdig med dodekaedern .

Monoedriska konvexa femkantiga plattor

Ett exempel på en femkantig platta med vinkeletiketter A,B,C,D och E, och kantlängdsetiketter a,b,c,d och e

Femton typer av konvexa femhörningar är kända för att kakla planet monohedriskt (dvs med en typ av kakel). Den senaste upptäcktes 2015. Denna lista har visats vara komplett av Rao (2017) (resultatet är föremål för referentgranskning). Bagina (2011) visade att det bara finns åtta kant-till-kant konvexa typer, ett resultat som erhålls oberoende av Sugimoto (2012) .

Michaël Rao från École normale supérieure de Lyon hävdade i maj 2017 att han hittat beviset på att det faktiskt inte finns några konvexa femhörningar som plattar utöver dessa 15 typer. Den 11 juli 2017 hade den första hälften av Raos bevis verifierats oberoende (datorkod tillgänglig) av Thomas Hales, professor i matematik vid University of Pittsburgh. I december 2017 var beviset ännu inte fullständigt peer-reviewed.

Varje uppräknad plattsättningsfamilj innehåller femhörningar som inte tillhör någon annan typ; dock kan vissa individuella femhörningar tillhöra flera typer. Dessutom tillåter vissa av femkanterna i de kända plattsättningstyperna också alternativa plattsättningsmönster utöver den standardplatta som alla delar av dess typ uppvisar.

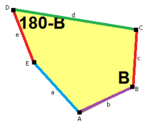
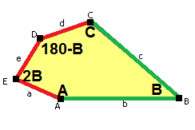
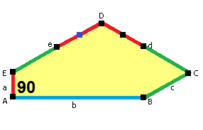
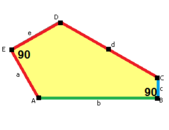
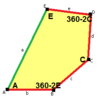
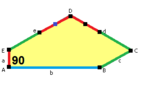
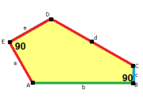
Sidorna av längden a , b , c , d , e är direkt medurs från vinklarna vid hörnen A , B , C , D , E respektive. ( A , B , C , D , E är alltså motsatta d , e , a , b , c respektive.)

15 monohedriska femkantiga plattor

1	2	3	4	5
B + C = 180° A + D + E = 360°	c = eB + D = 180°	a = b, d = c + e A = C = D = 120°	b = c, d = e B = D = 90°	a = b, d = e A = 60°, D = 120°
6	7	8	9	10
a = d = e, b = c B + D = 180°, 2B = E	b = c = d = eB + 2E = 2C + D = 360°	b = c = d = e2B + C = D + 2E = 360°	b = c = d = e2A + C = D + 2E = 360°	a = b = c + e A = 90°, B + E = 180° B + 2C = 360°
11	12	13	14	15
2a + c = d = e A = 90°, C + E = 180° 2B + C = 360°	2a = d = c + e A = 90°, C + E = 180° 2B + C = 360°	d = 2a = 2e B = E = 90° 2A + D = 360°	2a = 2c = d = e A = 90°, B ≈ 145,34°, C ≈ 69,32° D ≈ 124,66°, E ≈ 110,68° (2B + C = 360°, C + E = 180°)	a = c = e, b = 2a A = 150°, B = 60°, C = 135° D = 105°, E = 90°

Många av dessa monohedriska plattor har frihetsgrader. Dessa friheter inkluderar variationer av inre vinklar och kantlängder. I gränsen kan kanter ha längder som närmar sig noll eller vinklar som närmar sig 180°. Typerna 1, 2, 4, 5, 6, 7, 8, 9 och 13 tillåter parametriska möjligheter med icke-konvexa prototiler.

Periodiska plattsättningar kännetecknas av sin tapetgruppsymmetri , till exempel definieras p2 (2222) av fyra 2-faldiga rotationspunkter. Denna nomenklatur används i diagrammen nedan, där plattorna också är färgade av sina k -isohedriska positioner inom symmetrin.

En primitiv enhet är en del av plattsättningen som genererar hela plattsättningen med enbart översättningar och är så liten som möjligt.

Reinhardt (1918)

Reinhardt (1918) hittade de första fem typerna av femkantiga plattor. Alla fem kan skapa isoedriska plattsättningar, vilket innebär att symmetrierna i plattsättningen kan ta vilken som helst bricka till vilken annan bricka som helst (mer formellt agerar automorfismgruppen transitivt på plattorna).

B. Grünbaum och GC Shephard har visat att det finns exakt tjugofyra distinkta "typer" av isoedriska plattsättningar av planet med femhörningar enligt deras klassificeringsschema. Alla använder Reinhardts plattor, vanligtvis med ytterligare villkor som krävs för plattsättningen. Det finns två plattor av alla typ 2-brickor och en av alla av var och en av de andra fyra typerna. Femton av de andra arton plattorna är av speciella fall av typ 1-plattor. Nio av de tjugofyra plattorna är kant i kant.

Det finns också 2-isohedriska plattor i speciella fall av typ 1, typ 2 och typ 4 plattor, och 3-isohedriska plattor, alla kant-till-kant, genom speciella fall av typ 1 plattor. Det finns ingen övre gräns på k för k-isohedriska plattsättningar av vissa plattor som är både typ 1 och typ 2, och därmed inte heller på antalet plattor i en primitiv enhet.

Tapetgruppens symmetri för varje plattsättning anges, med orbifold notation inom parentes. En andra lägre symmetrigrupp ges om kakelkiralitet existerar , där spegelbilder anses vara distinkta. Dessa visas som gula och gröna brickor i dessa fall.

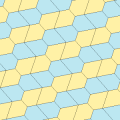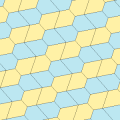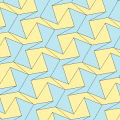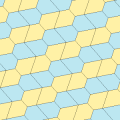
Typ 1

Det finns många beläggningstopologier som innehåller typ 1 pentagoner. Fem exempeltopologier ges nedan.

Kakelplattor av pentagon typ 1

p2 (2222)	cmm (2*22)	cm (*×)	pmg (22*)	pgg (22×)	p2 (2222)	cmm (2*22)
		p1 (°)	p2 (2222)	p2 (2222)
2-platta primitiv enhet			4-platta primitiv enhet
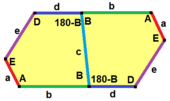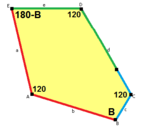
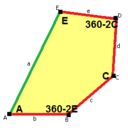
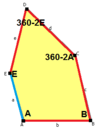
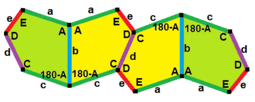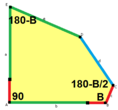
B + C = 180° A + D + E = 360°		a = c, d = e A + B = 180° C + D + E = 360°	a = c A + B = 180° C + D + E = 360°	a = e B + C = 180° A + D + E = 360°	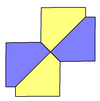d = c + e A = 90°, 2B + C = 360° C + D = 180°, B + E = 270°

Typ 2

Dessa typ 2-exempel är isoedriska. Den andra är en kant-till-kant-variation. De har båda pgg (22×) symmetri. Om spegelbildsplattor (gula och gröna) anses vara distinkta är symmetrin p2 (2222).

Typ 2

pgg (22×)
p2 (2222)
4-bricka primitiv enhet
c = eB + D = 180°	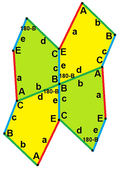c = e, d = b B + D = 180°

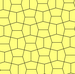
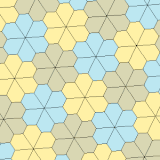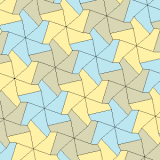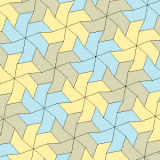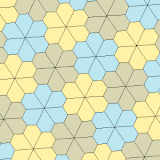
Typ 3, 4 och 5

Typ 3		Typ 4		Typ 5
p3 (333)	p31m (3*3)	p4 (442)	p4g (4*2)	p6 (632)
3-platta primitiv enhet		4-platta primitiv enhet		6-platts primitiv enhet		Primitiv enhet med 18 plattor
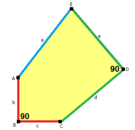
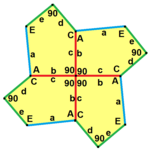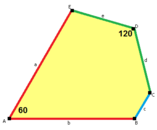
a = b, d = c + e A = C = D = 120°		b = c, d = e B = D = 90°		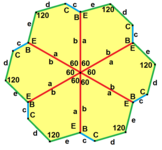a = b, d = e A = 60°, D = 120°		a = b = c, d = e A = 60°, B = 120°, C = 90° D = 120°, E = 150°

Kershner (1968) Typer 6, 7, 8

Kershner (1968) hittade ytterligare tre typer av femkantiga brickor, vilket gjorde det totala antalet till åtta. Han hävdade felaktigt att detta var den kompletta listan över femhörningar som kan belägga planet.

Dessa exempel är 2-isohedriska och kant-till-kant. Typ 7 och 8 har kirala kakelpar, som är färgade som par i gulgrönt och den andra som två nyanser av blått. Pgg-symmetrin reduceras till p2 när kirala par anses vara distinkta.

Typ 6	Typ 6 (även typ 5)	Typ 7	Typ 8
p2 (2222)		pgg (22×)	pgg (22×)
		p2 (2222)	p2 (2222)
a = d = e, b = c B + D = 180°, 2B = E	a = d = e, b = c, B = 60° A = C = D = E = 120°	b = c = d = eB + 2E = 2C + D = 360°	b = c = d = e2B + C = D + 2E = 360°
4-platta primitiv enhet	4-platta primitiv enhet	8-platts primitiv enhet	8-platts primitiv enhet

James (1975) Typ 10

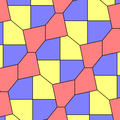
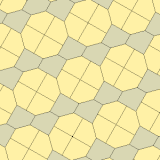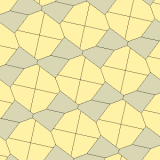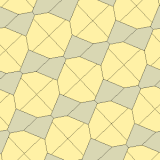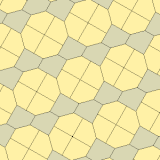
1975 hittade Richard E. James III en nionde typ, efter att ha läst om Kershners resultat i Martin Gardners " Matematical Games " kolumn i Scientific American magazine från juli 1975 (omtryckt i Gardner (1988) ). Den är indexerad som typ 10. Plattläggningen är 3-isohedrisk och icke-kant-till-kant.

Typ 10

p2 (2222)	cmm (2*22)
a=b=c+e A=90, B+E=180° B+2C=360°	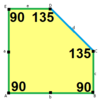a=b=2c=2e A=B=E=90° C=D=135°
6-platta primitiv enhet

Rice (1977) Typer 9,11,12,13

Marjorie Rice , en amatörmatematiker, upptäckte fyra nya typer av tesselerande femhörningar 1976 och 1977.

Alla fyra plattorna är 2-isohedriska. De kirala plattorna är färgade i gult och grönt för en isoedrisk uppsättning och två nyanser av blått för den andra uppsättningen. Pgg-symmetrin reduceras till p2 när de kirala paren anses vara distinkta.

Plattläggningen av typ 9-plattor är kant-till-kant, men de andra är det inte.

Varje primitiv enhet innehåller åtta brickor.

Typ 9	Typ 11	Typ 12	Typ 13
pgg (22×)
p2 (2222)
b=c=d=e 2A+C=D+2E=360°	2a+c=d=e A=90°, 2B+C=360° C+E=180°	2a=d=c+e A=90°, 2B+C=360° C+E=180°	d=2a=2e B=E=90°, 2A+D=360°
8-platts primitiv enhet	8-platts primitiv enhet	8-platts primitiv enhet	8-platts primitiv enhet

Stein (1985) Typ 14

En 14:e konvex pentagontyp hittades av Rolf Stein 1985.

Plattläggningen är 3-isohedrisk och icke-kant-till-kant. Den har helt bestämda brickor, utan frihetsgrader. De exakta proportionerna anges av ${\frac {b}{a}}={\sqrt {\frac {11{\sqrt {57}}-25}{8}} }$ och vinkeln B trubbig med $\sin(B)={\frac {{\sqrt {57}}-3}{8}}$ . Andra samband kan lätt härledas.

De primitiva enheterna innehåller sex respektive brickor. Den har p2 (2222) symmetri.

Typ 14

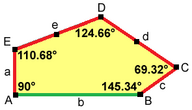2a=2c=d=e A=90°, B≈145,34°, C≈69,32°, D≈124,66°, E≈110,68° (2B+C=360°, C+E=180°).

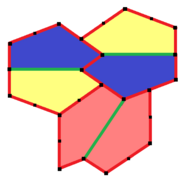6-platta primitiv enhet

Mann/McLoud/Von Derau (2015) Typ 15

University of Washington Bothells matematiker Casey Mann , Jennifer McLoud-Mann och David Von Derau upptäckte 2015 en 15:e monohedrisk kakelplatta konvex femhörning med hjälp av en datoralgoritm . Det är 3-isohedriskt och icke-kant-till-kant, ritat med 6 färger, 2 nyanser av 3 färger, som representerar kirala par av de tre isoedriska positionerna. Pgg-symmetrin reduceras till p2 när de kirala paren anses vara distinkta. Den har helt bestämda brickor, utan frihetsgrader. De primitiva enheterna innehåller tolv brickor respektive. Den har pgg (22×) symmetri och p2 (2222) om kirala par anses vara distinkta.

I juli 2017 slutförde Michaël Rao ett datorassisterat bevis som visar att det inte finns några andra typer av konvexa femhörningar som kan belägga planet. Den kompletta listan över konvexa polygoner som kan lägga till plattor i planet inkluderar ovanstående 15 femhörningar, tre typer av hexagoner och alla fyrhörningar och trianglar. En konsekvens av detta bevis är att det inte finns någon konvex polygon som bara delar planet en period, eftersom alla ovanstående typer tillåter en periodisk plattsättning.

Typ 15

(Större bild)

a=c=e, b=2a, d= a + √ 2 / √ 3 -1 A=150°, B=60°, C=135° D=105°, E=90°

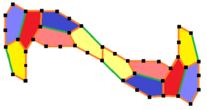Primitiv enhet med 12 plattor

Icke periodiska monohedriska femkanter plattsättningar

Ickeperiodiska monoedriska femkantiga plattor kan också konstrueras, som exemplet nedan med 6-faldig rotationssymmetri av Michael Hirschhorn. Vinklarna är A = 140°, B = 60°, C = 160°, D = 80°, E = 100°.

År 2016 kunde Bernhard Klaassen visa att varje diskret rotationssymmetrityp kan representeras av en monoedrisk femkantig plattsättning från samma klass av femhörningar. Exempel på 5-faldig och 7-faldig symmetri visas nedan. Sådana plattsättningar är möjliga för vilken typ av n -faldig rotationssymmetri som helst med n >2.

5-faldig rotationssymmetri i en monoedrisk femkantig plattsättning

Hirschhorns 6-faldiga rotationssymmetri monohedriska femkantiga plattor

7-faldig rotationssymmetri i en monoedrisk femkantig plattsättning

Dubbla enhetliga plattsättningar

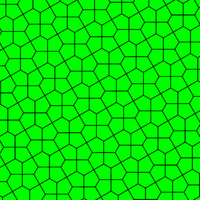
Det finns tre isoedriska femkantiga plattsättningar som genereras som dualer av de enhetliga plattsättningarna , de med 5-valens hörn. De representerar speciella fall med högre symmetri av de 15 monohedriska plattorna ovan. Enhetliga plattsättningar och deras dualer är alla kant till kant. Dessa dubbla plattsättningar kallas även Laves plattsättningar . Symmetrin för de enhetliga dubbla plattorna är densamma som de enhetliga plattorna. Eftersom de enhetliga plattorna är isogonala är dualerna isoedriska .

cmm (2*22)	p4g (4*2)	p6 (632)
Prismatisk femkantig plattsättning Förekomst av typ 1	Kairo pentagonal plattsättningsinstans av typ 4	Floret femkantig plattsättning Förekomst av typerna 1, 5 och 6
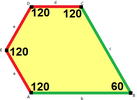
120°, 120°, 120°, 90°, 90° V3.3.3.4.4	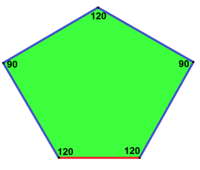120°, 120°, 90°, 120°, 90° V3.3.4.3.4	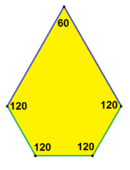120°, 120°, 120°, 120°, 60° V3.3.3.3.6

Dubbla k -enhetliga plattsättningar

De k -enhetliga plattorna med valens-5 hörn har också femkantiga dubbelplattor, som innehåller samma tre formade femhörningar som de halvregelbundna dualerna ovan, men innehåller en blandning av femkantiga typer. En k -uniform plattsättning har en k -isohedrisk dubbel plattsättning och representeras av olika färger och nyanser av färger nedan.

Till exempel är dessa 2-, 3-, 4- och 5-uniforma dualer alla femkantiga:

2-isohedral		3-isohedral
p4g (4*2)	pgg (22×)		p2 (2222)	p6 (*632)
4-isohedral			5-isohedral
pgg (22×)		p2 (2222)		p6m (*632)
5-isohedral
pgg (22×)			p2 (2222)

Pentagonal/hexagonal tessellation

Pentagonala underavdelningar av en hexagon

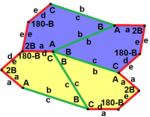
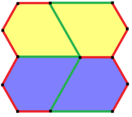
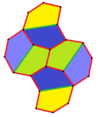
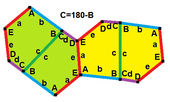
Pentagoner har ett speciellt förhållande till hexagoner. Som visas grafiskt nedan kan vissa typer av hexagoner delas in i femhörningar. Till exempel delar en vanlig hexagon i två typ 1-pentagoner. Underindelning av konvexa hexagoner är också möjlig med tre (typ 3), fyra (typ 4) och nio (typ 3) femhörningar.

I förlängningen av denna relation kan ett plan förses med en enda femkantig prototil form på sätt som genererar hexagonala överlägg. Till exempel:

Plan tessellation av en enda femkantig prototil (typ 1) med överlagringar av regelbundna hexagoner (var och en med 2 femhörningar).

Plan tessellation av en enda femkantig prototil (typ 3) med överlagringar av regelbundna hexagoner (var och en med 3 femhörningar).

Plan tessellation av en enda femkantig prototil (typ 4) med överlagringar av halvregelbundna hexagoner (var och en med 4 femhörningar).

Plan tessellation av en enda femkantig prototil (typ 3) med överlagringar av två storlekar av vanliga hexagoner (som omfattar 3 respektive 9 femhörningar).

Icke-konvexa femhörningar

Periodisk plattsättning av sfinxen

Med femhörningar som inte behöver vara konvexa är ytterligare typer av plattsättning möjliga. Ett exempel är sfinxen , en aperiodisk plattsättning som bildas av en femkantig reptil . Sfinxen kan också belägga planet med jämna mellanrum, genom att sätta ihop två sfinxplattor för att bilda ett parallellogram och sedan lägga till planet genom översättningar av detta parallellogram, ett mönster som kan förlängas till vilken som helst icke-konvex femhörning som har två på varandra följande vinklar som adderar till 2 π .

Det är möjligt att dela upp en liksidig triangel i tre kongruenta icke-konvexa femhörningar, som möts i triangelns mitt, och att belägga planet med den resulterande tre-pentagonenheten. En liknande metod kan användas för att dela in kvadrater i fyra kongruenta icke-konvexa femhörningar, eller vanliga hexagoner i sex kongruenta icke-konvexa femhörningar, och sedan planlägga planet med den resulterande enheten.

Regelbundna femkantiga plattsättningar i icke-euklidisk geometri

En dodekaeder kan betraktas som en vanlig plattsättning av 12 femhörningar på ytan av en sfär , med Schläfli-symbolen {5,3}, med tre femhörningar runt varje vertex.

I det hyperboliska planet finns det tilings av regelbundna femhörningar, till exempel order-4 pentagonal plattsättning , {5,4}, med fyra femhörningar runt varje vertex. Reguljära plattsättningar av högre ordning {5,n} kan konstrueras på det hyperboliska planet, som slutar på {5,∞}.

Sfär		Hyperboliskt plan
{5,2}	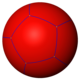{5,3}	{5,4}	{5,5}	{5,6}	{5,7}	{5,8}	...{5,∞}

Oregelbundna hyperboliska femkantiga plattor

Det finns ett oändligt antal dubbla enhetliga plattsättningar i hyperboliskt plan med isogonala oregelbundna femkantiga ytor. De har ansiktskonfigurationer som V3.3. s .3. q .

Beställ p - q floret femkantigt kakel

7-3	8-3	9-3	...	5-4	6-4	7-4	...	5-5
V3.3.3.3.7	V3.3.3.3.8	V3.3.3.3.9	...	V3.3.4.3.5	V3.3.4.3.6	V3.3.4.3.7	...	V3.3.5.3.5

Polygonal hyperbolisk binär plattsättning med 60-120-60-120-120-graders femhörningar

Den binära plattsättningen kan göras till en femkantig plattsättning om man ersätter de horocykliska kanterna med linjesegment.

Bibliografi

•    Bagina, Olga (2004), "Tiling the plane with congruent equilateral convex pentagons", Journal of Combinatorial Theory, Series A , 105 (2): 221–232, doi : 10.1016/j.jcta.2003.11.0096 -SN- SN- 0109 , IS 0899 , MR 2046081
•   Bagina, Olga (2011), Мозаики из выпуклых пятиугольников [Kapitelsättningar av planet med konvexa femhörningar], Vestnik (på ryska), 4 (48): 63–73, ISSN 2078-17628 , hämtad 20129 januari
• Bellos, Alex (11 augusti 2015), "Attacken på femhörningen resulterar i upptäckten av en ny matematisk bricka" , The Guardian
• Chavey, D. (1989), "Tilings by Regular Polygons—II: A Catalog of Tilings" , Computers & Mathematics with Applications , 17 ( 1–3): 147–165, doi : 10.1016/0898-1221(89)90156 -9
•    Gardner, Martin (1988), "Tiling with Convex Polygons", Time travel and other matematical bewilderments , New York: WH Freeman, Bibcode : 1988ttom.book.....G , ISBN 978-0-7167-1925-0 , MR 0905872
•   Gerver, ML (2003), "Theorems on tessellations by polygons", Sbornik: Mathematics , 194 (6): 879–895, Bibcode : 2003SbMat.194..879G , doi : 10.1070 /sm20006v 5be20006v 5be2007a , 402007a,402007a,40207a,40207a,402007a,402007a,402007a,40207a,40207a ,402007a, 40206,40207a 0813440
•   Godrèche, C. (1989), "The sphinx: a limit-periodic tiling of the plane", Journal of Physics A: Mathematical and General , 22 (24): L1163–L1166, Bibcode : 1989JPhA...22L1163G , doi : 10.1088/0305-4470/22/24/006 , MR 1030678
•    Grünbaum, Branko ; Shephard, Geoffrey C. (1978), "Isohedral tilings of the plane by polygons", Commentarii Mathematici Helvetici , 53 : 542–571, ​​doi : 10.1007/bf02566098 , ISSN 0010-25971 41928CID 71 049CID
•    Grünbaum, Branko ; Shephard, Geoffrey C. (1987), "Tilings by polygons", Tilings and Patterns , New York: WH Freeman and Company, ISBN 978-0-7167-1193-3 , MR 0857454
•    Hirschhorn, MD; Hunt, DC (1985), "Equilateral convex pentagons which tile the plane" (PDF) , Journal of Combinatorial Theory, Series A , 39 (1): 1–18, doi : 10.1016/0097-3165(85)90078-0 , ISSN 1096-0899 , MR 0787713 , hämtad 2020-10-30
•     Kershner, Richard (1968), "On paving the plane", American Mathematical Monthly , 75 (8): 839–844, doi : 10.2307/2314332 , ISSN 0002-9890 , JSTOR 2314332 , 82 MR 22366
•    Klaassen, Bernhard (2016), "Rotationssymmetriska plattsättningar med konvexa femhörningar och hexagoner", Elemente der Mathematik , 71 (4): 137–144, arXiv : 1509.06297 , doi : 10.4171/em/3101 , SSN 6101 , SSN 6101 , 7C 3101 , SSN 6101 , 7C 3101 , 7C 3101 738
•   Mann, Casey; McLoud-Mann, Jennifer; Von Derau, David (2018), "Convex pentagons that admit $i$ -block transitive tilings", Geometriae Dedicata , 194 (1): 141–167, arXiv : 1510.01186 , doi : 10.1017-1017701/s1 -9 , S2CID 119176351
• Rao, Michaël (2017), Uttömmande sökning av konvexa femhörningar som belägger planet (PDF) , arXiv : 1708.00274
• Reinhardt, Karl (1918), Über die Zerlegung der Ebene in Polygone (Dissertation) (på tyska), Borna-Leipzig: Druck von Robert Noske
•     Schattschneider, Doris (1978), "Tiling the plane with congruent pentagons" , Mathematics Magazine , 51 (1): 29–44, doi : 10.2307/2689644 , ISSN 0025-570X , JSTOR 26896449 , 7MR 6449
• Schattschneider, Doris (1985), "A new pentagon kakelläggare", Mathematics Magazine , 58 (5): 308, Omslaget har en bild av den nya plattsättningen
•   Sugimoto, Teruhisa; Ogawa, Tohru (2005), "Systematisk studie av konvexa femkantiga plattor. I. Fall av konvexa femhörningar med fyra lika långa kanter" , Forma , 20 : 1–18, MR 2240616
•   Sugimoto, Teruhisa; Ogawa, Tohru (2009), "Systematisk studie av konvexa femkantiga plattor, II: plattsättningar av konvexa femhörningar med fyra lika långa kanter" , Forma , 24 ( 3): 93–109, MR 2868775 ; Errata , Forma 25 (1): 49, 2010, MR 2868824
•   Sugimoto, Teruhisa (2012), "Konvexa femhörningar för kant-till-kant plattsättning, I" , Forma , 27 ( 1): 93–103, MR 3030316
• Wolchover, Natalie (11 juli 2017), "Pentagon Tiling Proof Solves Century-Old Math Problem" , Quanta Magazine

externa länkar

• Weisstein, Eric W. , "Pentagon Tiling" , MathWorld
• Pentagon plattor
• De 14 Pentagonerna som belägger planet
• 15 (monoedriska) plattor med en konvex femkantig kakel med k-isohedriska färger
• Kod för att visa den 14:e pentagontypen
• Kod för att visa den 15:e pentagontypen