Wythoff konstruktion
Inom geometrin är en Wythoff-konstruktion , uppkallad efter matematikern Willem Abraham Wythoff , en metod för att konstruera en enhetlig polyeder eller plan plattsättning . Den kallas ofta för Wythoffs kalejdoskopiska konstruktion.
Byggprocess
Metoden bygger på idén att kakla en sfär , med sfäriska trianglar – se Schwarz trianglar . Denna konstruktion arrangerar tre speglar vid sidorna av en triangel, som i ett kalejdoskop . Men till skillnad från ett kalejdoskop är speglarna inte parallella, utan skär varandra i en enda punkt. De omsluter därför en sfärisk triangel på ytan av vilken sfär som helst som är centrerad på den punkten och upprepade reflektioner producerar en mängd kopior av triangeln. Om vinklarna för den sfäriska triangeln väljs på lämpligt sätt, kommer trianglarna att lägga till sfären en eller flera gånger.
Om man placerar en vertex vid en lämplig punkt inuti den sfäriska triangeln som omges av speglarna, är det möjligt att säkerställa att reflektionerna av den punkten ger en enhetlig polyeder. För en sfärisk triangel ABC har vi fyra möjligheter som kommer att producera en enhetlig polyeder:
- En vertex är placerad i punkten A . Detta ger en polyeder med Wythoff-symbolen a | b c , där a är lika med π dividerat med triangelns vinkel vid A , och på samma sätt för b och c .
- En vertex placeras i en punkt på linjen AB så att den delar vinkeln vid C . Detta ger en polyeder med Wythoff-symbolen a b | c .
- En vertex placeras så att den är i mitten av ABC . Detta ger en polyeder med Wythoff-symbolen a b c |.
- Spetsen är vid en punkt så att, när den roteras runt något av triangelns hörn med två gånger vinkeln vid den punkten, förskjuts den med samma avstånd för varje vinkel. Endast jämna numrerade reflektioner av den ursprungliga vertexen används. Polyedern har Wythoff-symbolen | a b c .
Processen i allmänhet gäller även för högredimensionella vanliga polytoper , inklusive de 4-dimensionella enhetliga 4-polytoperna .
  Det hexagonala prismat är konstruerat från både (6 2 2) och (3 2 2) familjerna. |
  Den stympade kvadratiska plattsättningen är konstruerad av två olika symmetripositioner i (4 4 2) familjen. |
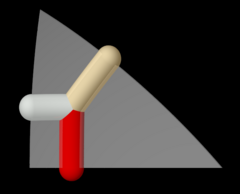 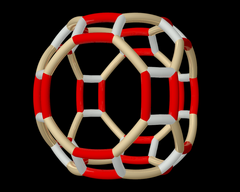 Wythoff mönster pq2| = 432|. Bana av Wythoff-mönstret ovan under verkan av hela oktaedriska gruppen . |
Icke-wythoffska konstruktioner
Uniforma polytoper som inte kan skapas genom en Wythoff-spegelkonstruktion kallas icke-Wythoffian. De kan i allmänhet härledas från Wythoffian former antingen genom alternering (borttagning av alternerande hörn) eller genom att infoga omväxlande lager av delfigurer. Båda dessa typer av figurer kommer att innehålla rotationssymmetri. Ibland snubformer som Wythoffian, även om de bara kan konstrueras genom växling av omnitruncerade former.
 Det hexagonala antiprismat är konstruerat genom en växling av ett tvåsidigt prisma . |
 Den långsträckta triangulära plattsättningen är uppbyggd av en skiktning av kvadratisk plattsättning och triangulära plattsättningsrader . |
 Den stora dirhombicosidodecahedronen är den enda icke-wythoffska enhetliga polyedern. |
Se även
- Wythoff-symbol - en symbol för Wythoff-konstruktionen av enhetliga polyedrar och enhetliga plattsättningar .
- Coxeter–Dynkin-diagram - en generaliserad symbol för Wythoff-konstruktionen av enhetliga polytoper och bikakor.
- Coxeter Regular Polytopes , tredje upplagan, (1973), Dover upplagan, ISBN 0-486-61480-8 (Kapitel V: Kalejdoskopet, avsnitt: 5.7 Wythoffs konstruktion)
- Coxeter The Beauty of Geometry: Twelve Essays , Dover Publications, 1999, ISBN 0-486-40919-8 (Kapitel 3: Wythoff's Construction for Uniform Polytopes)
- Har'El, Z. Uniform Solution for Uniform Polyhedra. , Geometriae Dedicata 47, 57-110, 1993. [1] (Avsnitt 4: Kalejdoskopet)
- WA Wythoff , En relation mellan polytoperna i C600-familjen , Koninklijke Akademie van Wetenschappen te Amsterdam, Proceedings of the Section of Sciences, 20 (1918) 966–970.
externa länkar
- Greg Egans applet för att visa enhetliga polyedrar med Wythoffs konstruktionsmetod
- En Shadertoy-rendering av Wythoffs konstruktionsmetod
- Jenn , programvara som genererar vyer av (sfäriska) polyedrar och polychora från symmetrigrupper


