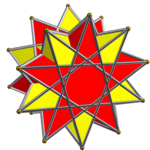
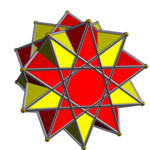
Prismatisk sammansättning av antiprismor

Förening av n p / q -gonala antiprismor
n =2 5/3-gonal 5/2-gonal
Typ	Enhetlig sammansättning
Index	q udda: UC 23 q jämnt: UC 25
Polyhedra	n p / q -gonala antiprismor
Schläfli-symboler (n=2)	ß{2,2p/q} ßr{2,p/q}
Coxeter-diagram (n=2)
Ansikten	2 n { p / q } (om inte p / q =2), 2 np trianglar
Kanter	4 np
Vertices	2 np
Symmetrigrupp	nq udda: np -faldig antiprismatisk ( D np d ) nq jämn: np -faldig prismatisk ( D np h )
Undergrupp begränsar till en beståndsdel	q udda: p -faldigt antiprismatisk ( D p d ) q jämn: p -faldig prismatisk ( D p h )

Inom geometrin är en prismatisk sammansättning av antiprisma en kategori av enhetlig polyhedronförening . Varje medlem av denna oändliga familj av enhetliga polyhedronföreningar är ett symmetriskt arrangemang av antiprismor som delar en gemensam rotationssymmetriaxel.

Oändlig familj

Denna oändliga familj kan räknas upp enligt följande:

• För varje positivt heltal n ≥1 och för varje rationellt tal p / q >3/2 (uttryckt med p och q coprime ), förekommer föreningen av n p / q -gonala antiprismor, med symmetrigrupp:
  • D _{np d} om nq är udda
  • D _{np h} om nq är jämnt

Där p / q =2 är komponenten tetraedern (eller dyadisk antiprisma). I detta fall, om Oh _n = 2 är föreningen stella octangula , med högre symmetri ( ).

Föreningar av två antiprismor

Föreningar av två n -antiprismor delar sina hörn med ett 2 n - prisma och existerar som två alternerade uppsättningar av hörn.

Kartesiska koordinater för hörn av ett antiprisma med n -gonala baser och likbenta trianglar är

• $\left(\cos {\frac {k\pi }{n}},\sin {\frac {k\pi }{n}},(-1)^{k}h\höger)$
• $\left(\cos {\frac {k\pi }{n}},\sin {\frac {k \pi }{n}},(-1)^{k+1}h\höger)$

med k från 0 till 2 n −1; om trianglarna är liksidiga,

$2h^{2}=\cos {\frac {\pi }{n}}-\cos {\frac {2\pi }{n}}.$

Föreningar av 2 antiprismor

2 digonala antiprismor (tetraedrar)	2 triangulära antiprismor (oktaedrar)	2 fyrkantiga antiprismor	2 hexagonala antiprismor	2 pentagrammiska korsade antiprisma

Sammansättning av två trapezoedrar (dubbel)

Dualerna av den prismatiska sammansättningen av antiprismor är sammansättningar av trapezoedrar :

Två kuber (trigonala trapetzoeder)

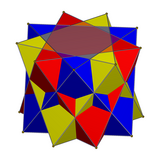
Sammansättning av tre antiprismor

För föreningar med tre digonala antiprismor roteras de 60 grader, medan tre triangulära antiprismor roteras 40 grader.

Tre tetraedrar	Tre oktaedrar

•   Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society , 79 ( 3): 447–457, doi : 10.1017/S0305004100052440 , MR 0397554 .