Dodecagon

Vanlig dodecagon
Vanlig dodecagon
	En vanlig dodecagon
Typ	Vanlig polygon
Kanter och hörn	12
Schläfli symbol	{12}, t{6}, tt{3}
Coxeter–Dynkin-diagram	;
Symmetrigrupp	Dihedral (D 12 ), beställning 2×12
Inre vinkel ( grader )	150°
Egenskaper	Konvex , cyklisk , liksidig , isogonal , isotoxal
Dubbel polygon	Själv

I geometri är en tolvkant eller 12-gon vilken tolvsidig polygon som helst .

Vanlig dodecagon

Tre kvadrater av sidorna R kan skäras och ordnas om till en dodekagon med cirkumradien R , vilket ger ett bevis utan ord att dess area är 3 R ²

En vanlig dodecagon är en figur med sidor av samma längd och inre vinklar av samma storlek. Den har tolv linjer med reflekterande symmetri och rotationssymmetri av ordning 12. En vanlig tvåkantslinje representeras av Schläfli-symbolen {12} och kan konstrueras som en trunkerad hexagon , t{6}, eller en två gånger trunkerad triangel tt{3 }. Den inre vinkeln vid varje hörn av en vanlig dodecagon är 150°.

Område

Arean av en vanlig dodecagon med sidolängd a ges av:

{\begin{aligned}A&=3\cot \left({\frac {\pi }{12 }}\right)a^{2}=3\left(2+{\sqrt {3}}\right)a^{2}\\&\simeq 11.19615242\,a^{2}\end{aligned} }

Och när det gäller apotem r (se även inskriven figur ) är området:

{\begin{aligned}A&=12\tan \left({\frac {\pi }{12 }}\right)r^{2}=12\left(2-{\sqrt {3}}\right)r^{2}\\&\simeq 3.2153903\,r^{2}\end{aligned} }

När det gäller cirkumradius R är området:

A=6\sin \left({\frac {\pi }{6}}\right)R^{2}=3R^{2 }

Spännvidden S för dodecagonen är avståndet mellan två parallella sidor och är lika med två gånger apotem. En enkel formel för area (given sidlängd och spännvidd) är:

A=3aS

Detta kan verifieras med det trigonometriska förhållandet:

S=a(1+2\cos {30^{\circ }}+2\cos {60^{\circ }} )

Omkrets

Omkretsen av en vanlig dodecagon i termer av cirkumradius är:

{\begin{aligned}p&=24R\tan \left({\frac {\pi }{12}}\right) =12R{\sqrt {2-{\sqrt {3}}}}\\&\simeq 6.21165708246\,R\end{aligned}}

Omkretsen i termer av apotem är:

{\begin{aligned}p&=24r\tan \left({\frac {\pi }{12}}\ höger)=24r(2-{\sqrt {3}})\\&\simeq 6.43078061835\,r\end{aligned}}

Denna koefficient är dubbelt så stor som koefficienten som finns i apotemekvationen för area.

Dodecagon konstruktion

Eftersom 12 = 2 ² × 3 kan en vanlig dodecagon konstrueras med hjälp av kompass- och rakkonstruktion :

Konstruktion av en vanlig dodecagon vid en given omsluten cirkel

Konstruktion av en vanlig dodecagon vid en given sidolängd, animation. (Konstruktionen är mycket lik den för oktagon vid en given sidolängd .)

Dissektion

12-kub	60 romb dissektion

Isotoxal dodekagon

Coxeter säger att varje zonogon (en 2 m -gon vars motsatta sidor är parallella och lika långa) kan dissekeras i m ( m -1)/2 parallellogram. I synnerhet gäller detta regelbundna polygoner med jämnt många sidor, i vilket fall parallellogrammen alla är rombi. För den vanliga dodecagonen , m =6, och den kan delas in i 15: 3 rutor, 6 breda 30° rhombs och 6 smala 15° rhombs. Denna nedbrytning är baserad på en Petrie- polygonprojektion av en 6-kub , med 15 av 240 ytor. Sekvensen OEIS-sekvens A006245 definierar antalet lösningar som 908, inklusive upp till 12-faldiga rotationer och kirala former i reflektion.

Dissektion i 15 romber
6-kub

Ett av sätten som de matematiska manipulativa mönsterblocken används på är att skapa ett antal olika dodecagoner. De är besläktade med de rombiska dissektionerna, med 3 60° romber sammanslagna i hexagoner, halvhexagon-trapetser eller uppdelade i 2 liksidiga trianglar.

Andra vanliga dissektioner
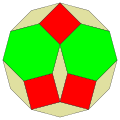		Socolar kakel	Mönsterblock

Symmetri

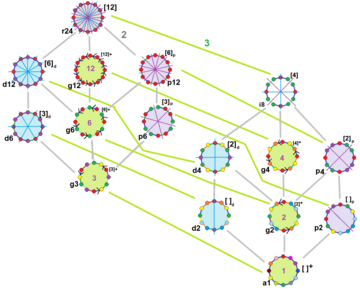
Symmetrierna för en vanlig dodecagon som visas med färger på kanter och hörn. John Conway märker dessa nedre symmetrier med en bokstav och ordningen på symmetrin följer bokstaven. Han ger d (diagonal, diasymmetri) med spegellinjer genom hörn, p med spegellinjer genom kanter (vinkelräta, persymmetri) i med spegellinjer genom både hörn och kanter (isosymmetri), och g för rotation (gyrosymmetri). a1 etiketter asymmetri. Dessa lägre symmetrier tillåter grader av friheter när det gäller att definiera oregelbundna dodekagoner.

Den vanliga dodekagonen har Dih _12- symmetri, ordning 24. Det finns 15 distinkta undergrupper av dihedriska och cykliska symmetrier. Varje undergruppssymmetri tillåter en eller flera frihetsgrader för oregelbundna former. Endast g12 -undergruppen har inga frihetsgrader utan kan ses som riktade kanter .

Exempel på dodecagoner av symmetri
r24
d12	g12	sid 12	i8
d6	g6	s6	d4	g4	p4
g3			d2	g2	p2
a1

Förekomst

Kakelsättning

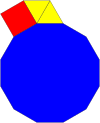
En vanlig dodecagon kan fylla en plan vertex med andra regelbundna polygoner på fyra sätt:

3.12.12	4.6.12	3.3.4.12	3.4.3.12

Här är 3 exempel på periodiska planbeläggningar som använder vanliga dodecagoner, definierade av deras vertexkonfiguration :

1-uniform		2-uniform
3.12.12	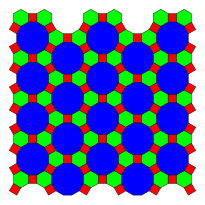4.6.12	3.12.12; 3.4.3.12

Skev dodecagon

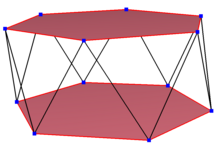
En vanlig sned dodecagon ses som sicksackande kanter på en sexkantig antiprisma .

En sned dodekagon är en sned polygon med 12 hörn och kanter men som inte finns på samma plan. Det inre av en sådan dodecagon är inte allmänt definierad. En sned sicksack-dodekagon har hörn som växlar mellan två parallella plan.

En vanlig sned dodecagon är vertextransitiv med lika kantlängder. I 3-dimensioner kommer det att vara en sicksack skev dodekagon och kan ses i hörnen och sidokanterna på ett hexagonalt antiprisma med samma D _5d , [2 ⁺ ,10] symmetri, ordning 20. Den dodekagrammiska antiprisman, s{ 2,24/5} och dodekagrammisk korsad antiprisma, s{2,24/7} har också vanliga sneda dodekagoner.

Petrie polygoner

Den vanliga dodecagonen är Petrie-polygonen för många högre dimensionella polytoper, ses som ortogonala projektioner i Coxeter-plan . Exempel i 4 dimensioner är 24-cells , snub 24-cells , 6-6 duoprism , 6-6 duopyramid . I 6 dimensioner 6-kub , 6-ortoplex , 2 ₂₁ , 1 ₂₂ . Det är också Petrie-polygonen för den stora 120-cellen och den stora 120-cellen .

Vanliga sneda dodecagoner i högre dimensioner
E ₆		F ₄		2G ₂ (4D)
2 ₂₁	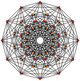1 ₂₂	24-celler	Snub 24-celler	6-6 duopyramid	{6}×{6}
A ₁₁	D ₇		B ₆		4A ₂
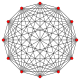11-simplex	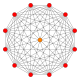(4 ₁₁ )	1 ₄₁	6-ortoplex	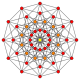6-kub	{3}×{3}×{3}×{3}

Relaterade figurer

Ett dodekagram är en 12-sidig stjärnpolygon, representerad av symbolen {12/n}. Det finns en vanlig stjärnpolygon : {12/5}, som använder samma hörn, men ansluter var femte punkt. Det finns också tre föreningar: {12/2} reduceras till 2{6} som två hexagoner och {12/3} reduceras till 3{4} som tre kvadrater , {12/4} reduceras till 4{3 } som fyra trianglar, och {12/6} reduceras till 6{2} som sex degenererade digoner .

Stjärnor och föreningar
n	1	2	3	4	5	6
Form	Polygon	Föreningar			Stjärnpolygon	Förening
Bild	{12/1} = {12}	{12/2} eller 2{6}	{12/3} eller 3{4}	{12/4} eller 4{3}	{12/5}	{12/6} eller 6{2}

Djupare trunkationer av den vanliga dodekagonen och dodekagrammen kan producera isogonala ( vertextransitiva ) mellanliggande stjärnpolygonformer med lika åtskilda hörn och två kantlängder. En trunkerad hexagon är en tolvhörning, t{6}={12}. En kvasitrunkerad hexagon, inverterad som {6/5}, är ett dodekagram: t{6/5}={12/5}.

Vertex-transitiva trunkationer av hexagonen
Kvasiregelbunden	Isogonal		Kvasiregelbunden
t{6}={12}			t{6/5}={12/5}

Exempel i användning

I blockbokstäver har bokstäverna E , H och X (och I i ett serif- teckensnitt) tvåsidiga konturer. Ett kors är en dodecagon, liksom logotypen för Chevrolet bildivision.

Vera Cruz-kyrkan i Segovia

Den vanliga dodecagonen har en framträdande plats i många byggnader. Torre del Oro är ett tvåårigt militärt vakttorn i Sevilla , södra Spanien , byggt av Almohad-dynastin . Det tidiga trettonde århundradet Vera Cruz-kyrkan i Segovia , Spanien är tvåårig. Ett annat exempel är Porta di Venere (Venusporten), i Spello , Italien , byggd på 1:a århundradet f.Kr. har två tvåsidiga torn, kallade "Propertius torn".