Order-4 hexagonal kakel bikaka
| Order-4 hexagonal kakel honeycomb | |
|---|---|
 Perspektiv projektionsvy inom Poincaré diskmodell |
|
| Typ |
Hyperbolisk vanlig honeycomb Paracompact enhetlig honeycomb |
| Schläfli symboler |
{6,3,4} {6,3 1,1 } t 0,1 {(3,6) 2 } |
| Coxeter diagram |
 ↔ ↔ ↔ ↔ ↔ ↔ |
| Celler |
{6,3} |
| Ansikten | hexagon {6} |
| Kantfigur | kvadrat {4} |
| Vertex figur |
 oktaeder |
| Dubbel | Beställ-6 kubisk honungskaka |
| Coxeter grupper |
, [4,3,6] , [6, 3 1,1 ] , [(6,3) [2] ] |
| Egenskaper | Regelbunden, nästan regelbunden |
Inom området hyperbolisk geometri uppstår den sexkantiga bikakan av ordning 4 som en av 11 vanliga parakompakta bikakor i 3-dimensionell hyperbolisk rymd . Den är parakompakt eftersom den har celler som består av ett oändligt antal ansikten. Varje cell är en hexagonal plattsättning vars hörn ligger på en horosfär : ett platt plan i hyperbolisk rymd som närmar sig en enda idealpunkt i oändligheten.
En geometrisk bikaka är en rymdfyllning av polyedriska eller högre dimensionella celler , så att det inte finns några luckor. Det är ett exempel på den mer allmänna matematiska plattsättningen eller tessellationen i valfritt antal dimensioner.
Bikakor konstrueras vanligtvis i vanligt euklidiskt ("platt") utrymme, som de konvexa enhetliga bikakorna . De kan också konstrueras i icke-euklidiska utrymmen , såsom hyperboliska enhetliga honeycombs . Vilken ändlig enhetlig polytop som helst kan projiceras till sin omkrets för att bilda en enhetlig bikaka i sfäriskt utrymme.
Schläfli -symbolen för den sexkantiga bikakan av ordning 4 är {6,3,4}. Eftersom den för den sexkantiga plattsättningen är {6,3} har denna bikaka fyra sådana sexkantiga plattor som möts vid varje kant. Eftersom Schläfli-symbolen för oktaedern är {3,4}, är vertexfiguren för denna bikake en oktaeder. Således möts åtta hexagonala plattor vid varje vertex av denna bikaka, och de sex kanterna som möts vid varje vertex ligger längs tre ortogonala axlar.
Bilder
 Perspektivprojektion |
 En cell, sett från utanför Poincare-sfären |
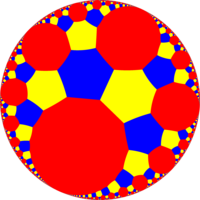 |
 Bikakan är analog med H 2 order-4 apeirogonal plattsättning , {∞,4}, som visas här med en grön apeirogon som beskrivs av dess horocykel |
Symmetri
Order-4 hexagonala bikakeplattor har tre reflekterande simplexsymmetrikonstruktioner.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Den halvsymmetriska enhetliga konstruktionen {6,3 1,1 } har två typer (färger) av hexagonala plattor, med Coxeter-diagram ↔ . En kvartssymmetrisk konstruktion finns också, med fyra färger av sexkantiga plattor: .
Den halvsymmetriska enhetliga konstruktionen {6,3 1,1 } har två typer (färger) av hexagonala plattor, med Coxeter-diagram ↔ . En kvartssymmetrisk konstruktion finns också, med fyra färger av sexkantiga plattor: .
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 Ytterligare två reflekterande symmetrier finns med icke-enkla fundamentala domäner: [6,3 * ,4], vilket är index 6, med Coxeter-diagram ; och [6,(3,4) * ], vilket är index 48. Det senare har en kubisk fundamental domän och ett oktaedriskt Coxeter-diagram med tre axiella oändliga grenar: . Det kan ses som att man använder åtta färger för att färga de hexagonala plattorna på honungskakan.
Ytterligare två reflekterande symmetrier finns med icke-enkla fundamentala domäner: [6,3 * ,4], vilket är index 6, med Coxeter-diagram ; och [6,(3,4) * ], vilket är index 48. Det senare har en kubisk fundamental domän och ett oktaedriskt Coxeter-diagram med tre axiella oändliga grenar: . Det kan ses som att man använder åtta färger för att färga de hexagonala plattorna på honungskakan.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Order-4 hexagonala bikakeplattor innehåller , som belägger 2- hypercykelytor och liknar den trunkerade triangulära plattsättningen i oändlig ordning , :
Order-4 hexagonala bikakeplattor innehåller , som belägger 2- hypercykelytor och liknar den trunkerade triangulära plattsättningen i oändlig ordning , :
Besläktade polytoper och bikakor
Order-4 hexagonal kakel honeycomb är en vanlig hyperbolisk honeycomb i 3-utrymmen, och en av 11 som är parakompakta.
| 11 paracompact vanliga honungskakor | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 {6,3,3} |
 {6,3,4} |
 {6,3,5} |
 {6,3,6} |
 {4,4,3} |
 {4,4,4} |
||||||
 {3,3,6} |
 {4,3,6} |
 {5,3,6} |
 {3,6,3} |
 {3,4,4} |
|||||||
Det finns femton enhetliga bikakor i [6,3,4] Coxeter- gruppfamiljen, inklusive denna vanliga form, och dess dubbla , ordningen -6 kubiska honeycomb .
| [6,3,4] familjens honungskakor | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| {6,3,4} | r{6,3,4} | t{6,3,4} | rr{6,3,4} | t 0,3 {6,3,4} | tr{6,3,4} | t 0,1,3 {6,3,4} | t 0,1,2,3 {6,3,4} | ||||

|

|

|

|

|

|

|

|
||||

|

|

|

|

|

|

|
|||||
| {4,3,6} | r{4,3,6} | t{4,3,6} | rr{4,3,6} | 2t{4,3,6} | tr{4,3,6} | t 0,1,3 {4,3,6} | t 0,1,2,3 {4,3,6} | ||||
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Den sexkantiga bikakan av ordning 4 har en besläktad alternerad bikaka, ↔ , med triangulär plattsättning och oktaederceller .
Den sexkantiga bikakan av ordning 4 har en besläktad alternerad bikaka, ↔ , med triangulär plattsättning och oktaederceller .
Det är en del av sekvensen av vanliga bikakor av formen {6,3,p}, som alla är sammansatta av hexagonala kakelceller:
| {6,3,p} honungskakor | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Plats | H 3 | ||||||||||
| Form | Paracompact | Icke-kompakt | |||||||||
| namn | {6,3,3} | {6,3,4} | {6,3,5} | {6,3,6} | {6,3,7} | {6,3,8} | ... {6,3,∞} | ||||
| Coxeter |
|
|
|
|
|
|
|
||||
| bild |

|

|

|

|

|

|

|
||||
|
Hönsfigur {3 , p} |
{3,3} |
{3,4} |
{3,5} |
{3,6} |
{3,7} |
{3,8} |
{3,∞} |
||||
Denna honeycomb är också relaterad till 16-cells , kubisk honeycomb och order-4 dodecahedral honeycomb , som alla har oktaedriska vertexfigurer.
| {s,3,4} vanliga bikakor | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Plats | S 3 | E 3 | H 3 | ||||||||
| Form | Ändlig | Affine | Kompakt | Paracompact | Icke-kompakt | ||||||
| namn |
{3,3,4} |
{4,3,4} |
{5,3,4} |
{6,3,4} |
{7,3,4} |
{8,3,4} |
... {∞,3,4} |
||||
| Bild |

|

|

|

|

|

|

|
||||
| Celler |
{3,3} |
{4,3} |
{5,3} |
{6,3} |
{7,3} |
{8,3} |
{∞,3} |
||||
Ovannämnda bikakor är också kvasiregelbundna:
| Regelbundna och kvasiregelbundna bikakor: {p,3,4} och {p,3 1,1 } | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Plats | Euklidiskt 4-utrymme | Euklidiskt 3-utrymme | Hyperboliskt 3-mellanslag | ||||||||
| namn |
{3,3,4} {3,3 1,1 } = |
{4,3,4} {4,3 1,1 } = |
{5,3,4} {5,3 1,1 } = |
{6,3,4} {6,3 1,1 } = |
|||||||
|
Coxeter diagram |
|
|
|
|
|||||||
| Bildceller {s |

|

|

|

|
|||||||
|
, 3} |
 |
 |
 |
 |
|||||||
Rättad order-4 hexagonal kakel honeycomb
| Rättad order-4 hexagonal kakel honeycomb | |
|---|---|
| Typ | Paracompact enhetlig honeycomb |
| Schläfli symboler | r{6,3,4} eller t 1 {6,3,4} |
| Coxeter diagram |
|
| Celler |
{3,4} r{6,3} |
| Ansikten |
triangel {3} sexkant {6} |
| Vertex figur |
 fyrkantigt prisma |
| Coxeter grupper |
, [4,3,6] , [4, 3 [3] ] , [6,3 1,1 ] , [3 []×[] ] |
| Egenskaper | Vertextransitiv, kanttransitiv |
![]()
![]()
![]()
![]()
![]()
![]()
![]() Den rätade ordnings-4 hexagonala bikakan , t 1 {6,3,4}, har oktaedriska och trihexagonala kakelfasetter, med en kvadratisk prisma vertexfigur .
Den rätade ordnings-4 hexagonala bikakan , t 1 {6,3,4}, har oktaedriska och trihexagonala kakelfasetter, med en kvadratisk prisma vertexfigur .
![]()
![]()
![]()
![]()
![]() Det liknar den 2D hyperboliska tetraapeirogonala plattsättningen , r{∞,4}, som alternerar apeirogonala och kvadratiska ytor:
Det liknar den 2D hyperboliska tetraapeirogonala plattsättningen , r{∞,4}, som alternerar apeirogonala och kvadratiska ytor:
Stympad order-4 sexkantig kakel bikaka
| Stympad order-4 sexkantig kakel bikaka | |
|---|---|
| Typ | Paracompact enhetlig honeycomb |
| Schläfli symbol | t{6,3,4} eller t 0,1 {6,3,4} |
| Coxeter diagram |
|
| Celler |
{3,4} t{6,3} |
| Ansikten |
triangel {3} dodecagon {12} |
| Vertex figur |
 fyrkantig pyramid |
| Coxeter grupper |
, [4,3,6] , [6, 3 1,1 ] |
| Egenskaper | Vertex-transitiv |
![]()
![]()
![]()
![]()
![]()
![]()
![]() Den avkortade sexkantiga bikakan av ordning 4 , t 0,1 {6,3,4}, har oktaeder och avkortade sexkantiga kakelfasetter, med en fyrkantig pyramidformad vertexfigur .
Den avkortade sexkantiga bikakan av ordning 4 , t 0,1 {6,3,4}, har oktaeder och avkortade sexkantiga kakelfasetter, med en fyrkantig pyramidformad vertexfigur .
![]()
![]()
![]()
![]()
![]() Det liknar den 2D hyperboliska trunkerade ordningen-4 apeirogonala plattorna , t{∞,4}, med apeirogonala och kvadratiska ytor:
Det liknar den 2D hyperboliska trunkerade ordningen-4 apeirogonala plattorna , t{∞,4}, med apeirogonala och kvadratiska ytor:
Bitruncated order-4 hexagonal kakel bikaka
| Bitruncated order-4 hexagonal kakel bikaka | |
|---|---|
| Typ | Paracompact enhetlig honeycomb |
| Schläfli symbol | 2t{6,3,4} eller t 1,2 {6,3,4} |
| Coxeter diagram |
|
| Celler |
t{4,3} t{3,6} |
| Ansikten |
kvadratisk {4} sexkant {6} |
| Vertex figur |
 digonal disfenoid |
| Coxeter grupper |
, [4,3,6] , [4, 3 [3] ] , [6,3 1,1 ] , [3 []×[] ] |
| Egenskaper | Vertex-transitiv |
![]()
![]()
![]()
![]()
![]()
![]()
![]() Den bitrunkerade ordning-4 hexagonala plattsättningsbikakan , t 1,2 {6,3,4}, har trunkerade oktaederceller och hexagonala tegelceller , med en digonal disfenoid vertexfigur .
Den bitrunkerade ordning-4 hexagonala plattsättningsbikakan , t 1,2 {6,3,4}, har trunkerade oktaederceller och hexagonala tegelceller , med en digonal disfenoid vertexfigur .
Kantellerad order-4 hexagonal kakel bikaka
| Kantellerad order-4 hexagonal kakel bikaka | |
|---|---|
| Typ | Paracompact enhetlig honeycomb |
| Schläfli symbol | rr{6,3,4} eller t 0,2 {6,3,4} |
| Coxeter diagram |
|
| Celler |
r{3,4} {}x{4} rr{6,3} |
| Ansikten |
triangel {3} kvadrat {4} sexkant {6} |
| Vertex figur |
 kil |
| Coxeter grupper |
, [4,3,6] , [6, 3 1,1 ] |
| Egenskaper | Vertex-transitiv |
![]()
![]()
![]()
![]()
![]()
![]()
![]() Den hexagonala bikakan med kantellerad ordning 4 , t 0,2 {6,3,4}, har cuboctahedron- , kub- och rhombitrihexagonala kakelceller, med en kilformad vertexfigur .
Den hexagonala bikakan med kantellerad ordning 4 , t 0,2 {6,3,4}, har cuboctahedron- , kub- och rhombitrihexagonala kakelceller, med en kilformad vertexfigur .
Cantitruncated order-4 hexagonal kakel bikaka
| Cantitruncated order-4 hexagonal kakel bikaka | |
|---|---|
| Typ | Paracompact enhetlig honeycomb |
| Schläfli symbol | tr{6,3,4} eller t 0,1,2 {6,3,4} |
| Coxeter diagram |
|
| Celler |
t{3,4} {}x{4} tr{6,3} |
| Ansikten |
fyrkantig {4} hexagon {6} dodecagon {12} |
| Vertex figur |
 spegelvänd sphenoid |
| Coxeter grupper |
, [4,3,6] , [6, 3 1,1 ] |
| Egenskaper | Vertex-transitiv |
![]()
![]()
![]()
![]()
![]()
![]()
![]() Den cantitruncated order-4 hexagonala plattsättningsbikakan , t 0,1,2 {6,3,4}, har trunkerade oktaeder- , kub- och trunkerade trihexagonala kakelceller, med en spegelvänd sphenoid vertexfigur .
Den cantitruncated order-4 hexagonala plattsättningsbikakan , t 0,1,2 {6,3,4}, har trunkerade oktaeder- , kub- och trunkerade trihexagonala kakelceller, med en spegelvänd sphenoid vertexfigur .
Runcinated order-4 hexagonal kakel honeycomb
| Runcinated order-4 hexagonal kakel honeycomb | |
|---|---|
| Typ | Paracompact enhetlig honeycomb |
| Schläfli symbol | t 0,3 {6,3,4} |
| Coxeter diagram |
|
| Celler |
{4,3} {}x{4} {6,3} {}x{6} |
| Ansikten |
kvadratisk {4} sexkant {6} |
| Vertex figur |
 oregelbunden triangulär antiprisma |
| Coxeter grupper | , [4,3,6] |
| Egenskaper | Vertex-transitiv |
![]()
![]()
![]()
![]()
![]()
![]()
![]() Den runcinerade ordning-4 hexagonala kakelhonungskakan , t 0,3 {6,3,4}, har kub , hexagonal plattsättning och hexagonala prismaceller , med en oregelbunden triangulär antiprisma vertexfigur .
Den runcinerade ordning-4 hexagonala kakelhonungskakan , t 0,3 {6,3,4}, har kub , hexagonal plattsättning och hexagonala prismaceller , med en oregelbunden triangulär antiprisma vertexfigur .
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Den innehåller den 2D hyperboliska rhombitetrahexagonala plattsättningen , rr{4,6}, med fyrkantiga och sexkantiga ytor. Kakelplattan har även en halvsymmetrikonstruktion .
Den innehåller den 2D hyperboliska rhombitetrahexagonala plattsättningen , rr{4,6}, med fyrkantiga och sexkantiga ytor. Kakelplattan har även en halvsymmetrikonstruktion .

|
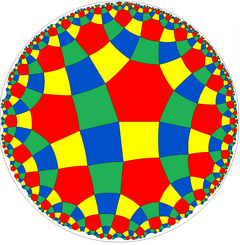
|
|
|
|
|---|
Runcitruncated order-4 hexagonal kakel honeycomb
| Runcitruncated order-4 hexagonal kakel honeycomb | |
|---|---|
| Typ | Paracompact enhetlig honeycomb |
| Schläfli symbol | t 0,1,3 {6,3,4} |
| Coxeter diagram |
|
| Celler |
rr{3,4} {}x{4} {}x{12} t{6,3} |
| Ansikten |
triangel {3} kvadrat {4} dodecagon {12} |
| Vertex figur |
likbent-trapesformad pyramid |
| Coxeter grupper | , [4,3,6] |
| Egenskaper | Vertex-transitiv |
![]()
![]()
![]()
![]()
![]()
![]()
![]() Den runcitrunkerade ordnings-4 hexagonala plattsättningsbikakan , t 0,1,3 {6,3,4}, har rombikuboktaeder , kub , tvåsidigt prisma och avkortade sexkantiga kakelceller, med en likbent trapetsformad pyramidformad vertexform .
Den runcitrunkerade ordnings-4 hexagonala plattsättningsbikakan , t 0,1,3 {6,3,4}, har rombikuboktaeder , kub , tvåsidigt prisma och avkortade sexkantiga kakelceller, med en likbent trapetsformad pyramidformad vertexform .
Runcicantellated order-4 hexagonal kakel bikaka
Den runcikantella ordning-4 hexagonala bikakan är densamma som den runcikantella ordningen-6 kubiska bikakan .
Omnitruncated order-4 hexagonal kakel bikaka
| Omnitruncated order-4 hexagonal kakel bikaka | |
|---|---|
| Typ | Paracompact enhetlig honeycomb |
| Schläfli symbol | t 0,1,2,3 {6,3,4} |
| Coxeter diagram |
|
| Celler |
tr{4,3} tr{6,3} {}x{12} {}x{8} |
| Ansikten |
kvadratisk {4} sexkant {6} oktagon {8} tvåhörning {12} |
| Vertex figur |
 oregelbunden tetraeder |
| Coxeter grupper | , [4,3,6] |
| Egenskaper | Vertex-transitiv |
![]()
![]()
![]()
![]()
![]()
![]()
![]() Den omnitrunkerade ordnings-4 hexagonala kakelhonungskakan , t 0,1,2,3 {6,3,4}, har stympad kuboktaeder , stympad trihexagonal plattsättning , tvåsidigt prisma och oktagonala prismaceller , med en oregelbunden tetrahedron vertexfigur .
Den omnitrunkerade ordnings-4 hexagonala kakelhonungskakan , t 0,1,2,3 {6,3,4}, har stympad kuboktaeder , stympad trihexagonal plattsättning , tvåsidigt prisma och oktagonala prismaceller , med en oregelbunden tetrahedron vertexfigur .
Alternerad ordning-4 hexagonal kakel bikaka
| Alternerad ordning-4 hexagonal kakel bikaka | |
|---|---|
| Typ |
Paracompact uniform honeycomb Halvregelbunden honeycomb |
| Schläfli symboler | h{6,3,4} |
| Coxeter diagram |
|
| Celler |
{3 [3] } {3,4} |
| Ansikten | triangel {3} |
| Vertex figur |
stympad oktaeder |
| Coxeter grupper | , [4,3 [3] ] |
| Egenskaper | Vertextransitiv, kanttransitiv, kvasiregelbunden |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Den alternerade ordningen-4 hexagonala plattsättningsbikakan , ↔ , är sammansatt av triangulära plattsättnings- och oktaederceller , i en stympad oktaederformad vertexfigur .
Den alternerade ordningen-4 hexagonala plattsättningsbikakan , ↔ , är sammansatt av triangulära plattsättnings- och oktaederceller , i en stympad oktaederformad vertexfigur .
Cantic order-4 hexagonal kakel honeycomb
| Cantic order-4 hexagonal kakel honeycomb | |
|---|---|
| Typ | Paracompact enhetlig honeycomb |
| Schläfli symboler | h 2 {6,3,4} |
| Coxeter diagram |
|
| Celler |
h 2 {6,3} t{3,4} r{3,4} |
| Ansikten |
triangel {3} kvadrat {4} sexkant {6} |
| Vertex figur |
 kil |
| Coxeter grupper | , [4,3 [3] ] |
| Egenskaper | Vertex-transitiv |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Den cantic order-4 hexagonala tegel honeycomb , ↔ , är sammansatt av trihexagonal plattsättning , trunkerade octahedron , och cuboctahedron celler, med en kil vertex figur .
Den cantic order-4 hexagonala tegel honeycomb , ↔ , är sammansatt av trihexagonal plattsättning , trunkerade octahedron , och cuboctahedron celler, med en kil vertex figur .
Runcic order-4 hexagonal kakel honeycomb
| Runcic order-4 hexagonal kakel honeycomb | |
|---|---|
| Typ | Paracompact enhetlig honeycomb |
| Schläfli symboler | h 3 {6,3,4} |
| Coxeter diagram |
|
| Celler |
{3 [3] } rr{3,4} {4,3} {}x{3} |
| Ansikten |
triangel {3} kvadrat {4} |
| Vertex figur |
 trekantig kupol |
| Coxeter grupper | , [4,3 [3] ] |
| Egenskaper | Vertex-transitiv |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Den runcic order-4 hexagonala tegel honeycomb , ↔ , är sammansatt av triangulära kakel , rhombicuboctahedron , kub och triangulära prisma celler, med en triangulär kupol vertex figur .
Den runcic order-4 hexagonala tegel honeycomb , ↔ , är sammansatt av triangulära kakel , rhombicuboctahedron , kub och triangulära prisma celler, med en triangulär kupol vertex figur .
Runcicantic order-4 hexagonal kakel bikaka
| Runcicantic order-4 hexagonal kakel bikaka | |
|---|---|
| Typ | Paracompact enhetlig honeycomb |
| Schläfli symboler | h 2,3 {6,3,4} |
| Coxeter diagram |
|
| Celler |
h 2 {6,3} tr{3,4} t{4,3} {}x{3} |
| Ansikten |
triangel {3} kvadrat {4} sexkant {6} oktagon {8} |
| Vertex figur |
 rektangulär pyramid |
| Coxeter grupper | , [4,3 [3] ] |
| Egenskaper | Vertex-transitiv |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Den runcicantic ordning-4 hexagonala tegel honeycomb , ↔ , är sammansatt av trihexagonal plattsättning , trunkerad cuboctahedron , trunkerad kub och triangulära prisma celler, med en rektangulär pyramid vertex figur .
Den runcicantic ordning-4 hexagonala tegel honeycomb , ↔ , är sammansatt av trihexagonal plattsättning , trunkerad cuboctahedron , trunkerad kub och triangulära prisma celler, med en rektangulär pyramid vertex figur .
Quarter order-4 hexagonal kakel honeycomb
| Quarter order-4 hexagonal kakel honeycomb | |
|---|---|
| Typ | Paracompact enhetlig honeycomb |
| Schläfli symbol | q{6,3,4} |
| Coxeter diagram |
|
| Celler |
{3 [3] } {3,3} t{3,3} h 2 {6,3} |
| Ansikten |
triangel {3} sexkant {6} |
| Vertex figur |
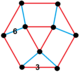 trekantig kupol |
| Coxeter grupper | , [3 []x[] ] |
| Egenskaper | Vertex-transitiv |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Kvartsordningen -4 hexagonala tetrahedronceller , q{6,3,4}, eller , består av triangulärt kakel , trihexagonalt plattsättning , tetraeder och trunkerade tetraederceller , med en triangulär kupolvertexfigur .
Kvartsordningen -4 hexagonala tetrahedronceller , q{6,3,4}, eller , består av triangulärt kakel , trihexagonalt plattsättning , tetraeder och trunkerade tetraederceller , med en triangulär kupolvertexfigur .
Se även
- Konvexa enhetliga bikakor i hyperboliskt utrymme
- Regelbundna tesselleringar av hyperboliskt 3-mellanslag
- Paracompact enhetliga honungskakor
- Coxeter , Regular Polytopes , 3:a. ed., Dover Publications, 1973. ISBN 0-486-61480-8 . (Tabell I och II: Vanliga polytoper och honeycombs, s. 294–296)
- The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN 99-35678 , ISBN 0-486-40919-8 (Kapitel 10, Regular Honeycombs in Hyperbolic Space ) Tabell III
- Jeffrey R. Weeks The Shape of Space, 2:a upplagan ISBN 0-8247-0709-5 (Kapitel 16-17: Geometries on Three-manifolds I,II)
-
Norman Johnson Uniform Polytopes , Manuskript
- NW Johnson : Theory of Uniform Polytopes and Honeycombs , Ph.D. Avhandling, University of Toronto, 1966
- NW Johnson: Geometries and Transformations , (2018) Kapitel 13: Hyperboliska Coxeter-grupper




















