Reptil
I tessellations geometri är en reptil eller reptil en form som kan dissekeras till mindre kopior av samma form . Termen myntades som en ordvits på djurreptiler av fritidsmatematikern Solomon W. Golomb och populariserades av Martin Gardner i hans " Matematical Games "-kolumn i maj 1963-numret av Scientific American . 2012 introducerade Lee Sallows en generalisering av reptiler som kallas self-tiling kakelset i Mathematics Magazine .
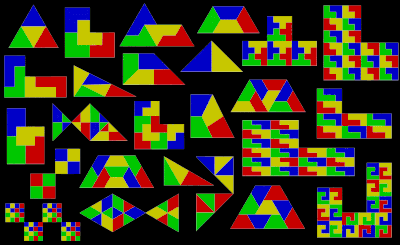
Terminologi
En reptil är märkt rep- n om dissektionen använder n kopior. En sådan form utgör nödvändigtvis prototilen för en plattsättning av planet, i många fall en aperiodisk plattsättning . En reptildissektion som använder olika storlekar av den ursprungliga formen kallas en oregelbunden reptil eller irreptil. Om dissektionen använder n kopior, sägs formen vara irrep- n . Om alla dessa sub-plattor är av olika storlekar så beskrivs plattsättningen dessutom som perfekt. En form som är rep- n eller irrep- n är trivialt också irrep-( kn − k + n ) för valfri k > 1, genom att ersätta den minsta brickan i rep- dissektionen med n ännu mindre brickor. Ordningen på en form, oavsett om du använder rep- eller irrep-plattor, är det minsta möjliga antalet brickor som räcker.
Exempel
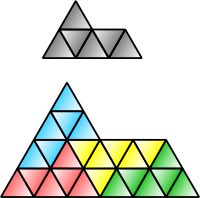
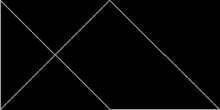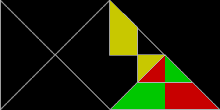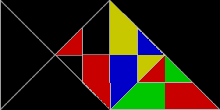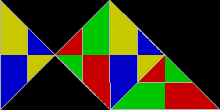
Varje kvadrat , rektangel , parallellogram , rhombus eller triangel är rep-4. Sfinxhexiamonden (illustrerad ovan) är rep-4 och rep-9, och är en av få kända självreplikerande femhörningar . Gosperön är rep-7 . Koch -snöflingan är irrep-7: sex små snöflingor av samma storlek, tillsammans med en annan snöflinga med tre gånger så stor yta som de mindre, kan kombineras för att bilda en enda större snöflinga.
En rätvinklig triangel med sidolängder i förhållandet 1:2 är rep-5, och dess rep-5-dissektion utgör grunden för den aperiodiska pinwheel-plattsättningen . Enligt Pythagoras sats har hypotenusan , eller den lutande sidan av rep-5-triangeln, en längd på √ 5 .
Den internationella standarden ISO 216 definierar storlekar på pappersark med hjälp av √ 2 , där långsidan av ett rektangulärt pappersark är kvadratroten av två gånger kortsidan av papperet. Rektanglar i denna form är rep-2. En rektangel (eller parallellogram) är rep- n om dess bildförhållande är √ n :1. En likbent rätvinklig triangel är också rep-2.
Rep-plattor och symmetri
Vissa reptiler, som den fyrkantiga och liksidiga triangeln , är symmetriska och förblir identiska när de reflekteras i en spegel . Andra, som sfinxen , är asymmetriska och finns i två distinkta former relaterade till spegelreflektion. Dissektion av sfinxen och några andra asymmetriska reptiler kräver användning av både den ursprungliga formen och dess spegelbild.
Rep-plattor och polyformer
Vissa reptiler är baserade på polyformer som polyiamanter och polyominoer , eller former skapade genom att lägga liksidiga trianglar och kvadrater kant i kant.
Rutor
Om en polyomino är likriktbar, det vill säga kan belägga en rektangel , så kommer den också att vara en rep-tile, eftersom rektangeln kommer att ha ett heltals sidlängdsförhållande och kommer därmed att belägga en kvadrat . Detta kan ses i octominoes , som skapas av åtta rutor. Två kopior av några octominoes kommer att belägga en kvadrat; därför är dessa oktominoer också rep-16 reptiler.
Fyra kopior av några nonominoer och nonakings kommer att belägga en kvadrat, därför är dessa polyformer också rep-36 rep-tiles.
Liksidiga trianglar
På samma sätt, om en polyiamond plattor en liksidig triangel, kommer den också att vara en rep-kakel.
Rätt trianglar
En rätvinklig triangel är en triangel som innehåller en rät vinkel på 90°. Två speciella former av rätvinklig triangel har uppmärksammats av reptilforskare, triangeln 45°-90°-45° och 30°-60°-90° triangeln.
45°-90°-45° trianglar
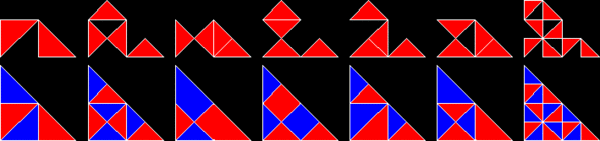
√2 baserade på likbenta rätvinkliga trianglar , med sidor i förhållandet 1:1: , är kända som polyabolos . Ett oändligt antal av dem är reptiler. Den enklaste av alla rep-plattor är faktiskt en enda likbent rätvinklig triangel. Den är rep-2 när den divideras med en enda linje som halverar den räta vinkeln mot hypotenusan . Rep-2 reptiler är också rep-2 n och rep-4,8,16+ trianglarna ger ytterligare reptiler. Dessa hittas genom att kassera hälften av underkopiorna och permutera resten tills de är spegelsymmetriska inom en rätvinklig triangel. Med andra ord kommer två kopior att lägga till en rätvinklig triangel. En av dessa nya reptiler påminner om fisken som bildas av tre liksidiga trianglar .
30°-60°-90° trianglar
Polyformer baserade på 30°-60°-90° rätvinkliga trianglar, med sidor i förhållandet 1 : √ 3 : 2, är kända som polydrafters . Vissa är identiska med polyminoer och polyiamanter , andra är distinkta.
Flera och olika rep-plattor
Många av de vanliga reptilerna är rep- n 2 för alla positiva heltalsvärden av n . I synnerhet gäller detta för tre trapetser inklusive den som bildas av tre liksidiga trianglar, för tre axelparallella hexagoner (L-tromino, L-tetromino och P-pentomino) och sfinxhexiamonden. Dessutom kan många reptiler, särskilt de med högre rep- n , självkaklas på olika sätt. Till exempel har rep-9 L-tetramino minst fjorton olika rep-beläggningar. Rep-9 sphinx hexiamond kan också kaklas på olika sätt.
Rep-plattor med oändliga sidor
De mest kända reptilerna är polygoner med ett ändligt antal sidor, men vissa former med ett oändligt antal sidor kan också vara reptiler. Till exempel är den teragoniska triangeln, eller horntriangeln, rep-4. Det är också ett exempel på en fraktal reptil .
Pentagonala reptiler
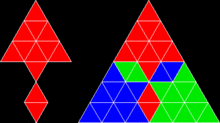
Triangulära och fyrsidiga (fyrsidiga) reptiler är vanliga, men femkantiga reptiler är sällsynta. Länge sfinxen var det enda kända exemplet, men den tyska / nyazeeländska matematikern Karl Scherer och den amerikanske matematikern George Sicherman har hittat fler exempel, inklusive en dubbelpyramid och en långsträckt version av sfinxen . Dessa femkantiga reptiler är illustrerade på Math Magic- sidorna som övervakas av den amerikanske matematikern Erich Friedman . Men sfinxen och dess utökade versioner är de enda kända femkanterna som kan reptileras med lika kopior. Se Clarkes reptilsidor .
Rep-plattor och fraktaler
Rep-plattor som fraktaler
Rep-plattor kan användas för att skapa fraktaler , eller former som är sig själva i mindre och mindre skalor. En reptilfraktal bildas genom att dela upp reptilen, ta bort en eller flera kopior av den uppdelade formen och sedan fortsätta rekursivt . Till exempel Sierpinski-mattan bildad på detta sätt från en rep-tegelsättning av en kvadrat till 27 mindre kvadrater, och Sierpinski-triangeln är bildad av en rep-platting av en liksidig triangel till fyra mindre trianglar. När en underkopia kasseras kan en rep-4 L- triomino användas för att skapa fyra fraktaler, varav två är identiska förutom orienteringen .
.gif)
.gif)
-2.gif)
-3.gif)
Fraktaler som rep-plattor
Eftersom fraktaler är sig själva lika i mindre och mindre skalor, kan många brytas ner till kopior av sig själva som en reptil. Men om fraktalen har en tom inre , kanske denna nedbrytning inte leder till en plattsättning av hela planet. Till exempel Sierpinski-triangeln rep-3, kaklad med tre kopior av sig själv, och Sierpinski-mattan är rep-8, kaklad med åtta kopior av sig själv, men upprepning av dessa nedbrytningar bildar inte en plattsättning. Å andra sidan drakkurvan en rymdfyllande kurva med ett icke-tomt inre; det är rep-4 och bildar en kakel. På liknande sätt Gosper-ön rep-7, bildad av den rymdfyllande Gosper-kurvan, och bildar återigen en plattsättning.
Genom konstruktion är vilken fraktal som helst som definieras av ett itererat funktionssystem av n sammandragande kartor med samma förhållande rep-n.
Oändlig plattsättning
Bland vanliga polygoner kan bara triangeln och kvadraten dissekeras till mindre lika stora kopior av sig själva. En vanlig hexagon kan dock dissekeras i sex liksidiga trianglar, som var och en kan dissekeras till en vanlig hexagon och ytterligare tre liksidiga trianglar. Detta är grunden för en oändlig plattsättning av hexagonen med hexagoner. Hexagonen är därför en irrep-∞ eller irrep-oändlighet irreptil.
Vanlig hexagon kaklad med oändliga kopior av sig själv
![Fractal elongated Koch snowflake (Siamese) tiled with infinite copies of itself[7]](//upload.wikimedia.org/wikipedia/commons/thumb/2/29/Frattale_infinito_rep-tile.gif/200px-Frattale_infinito_rep-tile.gif)
Fraktal långsträckt Koch snöflinga (siamesisk) kaklad med oändliga kopior av sig själv
![Fractal elongated Koch snowflake (Siamese) tiled with infinite copies of itself[7]](https://commons.wikimedia.org/wiki/File:Frattale_infinito_rep-tile.gif)
Se även
Anteckningar
- Gardner, M. (2001), "Rep-Tiles", The Colossal Book of Mathematics: Classic Puzzles, Paradoxes and Problems , New York: WW Norton, s. 46–58
- Gardner, M. (1991), "Kapitel 19: Rep-Tiles, Replicating Figures on the Plane", The Unexpected Hanging and Other Mathematical Diversions , Chicago, IL: Chicago University Press, s. 222–233
- Langford, CD (1940), "Uses of a Geometric Puzzle", The Mathematical Gazette , 24 (260): 209–211, doi : 10.2307/3605717
- Niţică, Viorel (2003), "Rep-tiles revisited", MASS selecta , Providence, RI: American Mathematical Society, s. 205–217, MR 2027179
- Sallows, Lee (2012), "On self-tiling tile sets", Mathematics Magazine , 85 (5): 323–333, doi : 10.4169/math.mag.85.5.323 , MR 3007213
- Scherer, Karl (1987), En förbryllande resa till reptilerna och besläktade djur
- Wells, D. (1991), The Penguin Dictionary of Curious and Interesting Geometry , London: Penguin, s. 213–214
externa länkar
Rep-plattor
- Mathematics Center Sphinx Album: http://mathematicscentre.com/taskcentre/sphinx.htm
- Clarke, AL "Reptiler." http://www.recmath.com/PolyPages/PolyPages/Reptiles.htm .
- Weisstein, Eric W. "Rep-Tile" . MathWorld .
- http://www.uwgb.edu/dutchs/symmetry/reptile1.htm (1999)
- IFStile - program för att hitta reptiler: https://ifstile.com
