Isoedrisk figur
Inom geometri är en tessellation med dimension 2 (en plan plattsättning) eller högre, eller en polytop med dimension 3 (en polyeder ) eller högre, isoedrisk eller ansiktstransitiv om alla dess ytor är desamma. Mer specifikt måste alla ansikten inte bara vara kongruenta utan måste vara transitiva , dvs måste ligga inom samma symmetriomlopp . Med andra ord, för alla två ytor A och B måste det finnas en symmetri av hela figuren genom translationer , rotationer och/eller reflektioner som mappar A till B . Av denna anledning konvexa isoedriska polyedrar de former som kommer att göra rättvisa tärningar .
Isoedriska polyedrar kallas isoedrar . De kan beskrivas av deras ansiktskonfiguration . En isoeder har ett jämnt antal ansikten.
Dualen av en isoedrisk polyeder är vertextransitiv, dvs isogonal. De katalanska fasta ämnena , bipyramiderna och trapezhedrarna är alla isoedriska . De är dualerna av de (isogonala) arkimediska fasta ämnena , prismor och antiprismor , respektive. De platoniska fasta ämnena , som antingen är självduala eller dubbla med en annan platonisk fast substans, är vertex-, kant- och ansiktstransitiva (dvs. isogonala, isotoxala och isoedriska).
En form som är isoedrisk, har regelbundna hörn och som dessutom är kanttransitiv (dvs isotoxal) sägs vara en kvasiregulär dual. Vissa teoretiker betraktar dessa figurer som verkligt kvasiregelbundna eftersom de delar samma symmetri, men detta är inte allmänt accepterat.
En polyeder som är isoedrisk och isogonal sägs vara ädel .
Inte alla isozonoedrar är isoedriska. Till exempel är en rombisk ikosaeder en isozonoeder men inte en isoeder.
Exempel
| Konvex | Konkav | ||
|---|---|---|---|
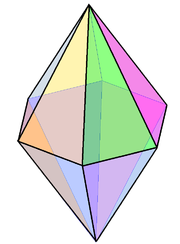 Hexagonala bipyramider , V4.4.6, är oregelbundna isoedriska polyedrar. |
 Kairos femkantiga plattsättning , V3.3.4.3.4, är isoedrisk. |
 Den rombiska dodekaedriska honungskakan är isoedrisk (och isokorisk och rymdfyllande). |
 En kvadratisk plattsättning förvrängd till en spiralformad H-platta (topologiskt ekvivalent) är fortfarande isoedrisk. |
Klasser av isoedrar genom symmetri
| Ansikten | Ansiktskonfiguration . |
Klass | namn | Symmetri | Beställa | Konvex | Coplanar | Icke konvex |
|---|---|---|---|---|---|---|---|---|
| 4 | V3 3 | Platonisk |
tetrahedron tetragonal disfenoid rombisk disfenoid |
T d , [3,3], (*332) D 2d , [2 + ,2], (2*) D 2 , [2,2] + , (222) |
24 4 4 4 |
 
|
||
| 6 | V3 4 | Platonisk |
kub trigonal trapezoeder asymmetrisk trigonal trapets |
O h , [4,3], (*432) D 3d , [2 + ,6] (2*3) D 3 [2,3] + , (223) |
48 12 12 6 |
 
|
||
| 8 | V4 3 | Platonisk |
oktaeder fyrkantig bipyramid rombisk bipyramid fyrkantig scalenohedron |
O h , [4,3], (*432) D 4h ,[2,4],(*224) D 2h ,[2,2],(*222) D 2d ,[2 + ,4],( 2*2) |
48 16 8 8 |
    
|

|
|
| 12 | V3 5 | Platonisk |
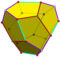
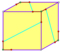
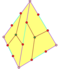
vanlig dodekaeder pyritohedron tetartoid |
I h , [5,3], (*532) Th , [3 + , 4], (3*2) T, [3,3] + , (*332) |
120 24 12 |
|
|
 
|
| 20 | V5 3 | Platonisk | vanlig ikosaeder | I h , [5,3], (*532) | 120 |  |
||
| 12 | V3.6 2 | katalanska | triakis tetraeder | T d , [3,3], (*332) | 24 |  |
 
|

|
| 12 | V(3.4) 2 | katalanska |
rombisk dodekaeder deltoidal dodekaeder |
O h , [4,3], (*432) T d , [3,3], (*332) |
48 24 |
  
|
 |
 
|
| 24 | V3.8 2 | katalanska | triakis oktaeder | Åh , [4,3], (*432 ) | 48 |  |
 
|
|
| 24 | V4.6 2 | katalanska | tetrakis hexaeder | Åh , [4,3], (*432 ) | 48 |
 
|
 
|
 
|
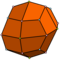
| 24 | V3.4 3 | katalanska | deltoidal icositetrahedron | Åh , [4,3], (*432 ) | 48 |
|
  
|

|
| 48 | V4.6.8 | katalanska | disdyakis dodekaeder | Åh , [4,3], (*432 ) | 48 |  |
  
|
 
|
| 24 | V3 4 .4 | katalanska | pentagonal icositetrahedron | O, [4,3] + , (432) | 24 |  |
||
| 30 | V(3,5) 2 | katalanska | rombisk triakontaeder | I h , [5,3], (*532) | 120 |  |
||
| 60 | V3.10 2 | katalanska | triakis icosahedron | I h , [5,3], (*532) | 120 |  |
   
|
|
| 60 | V5.6 2 | katalanska | pentakis dodekaeder | I h , [5,3], (*532) | 120 |  |
    
|
|
| 60 | V3.4.5.4 | katalanska | deltoidal hexecontahedron | I h , [5,3], (*532) | 120 |  |
 |

|
| 120 | V4.6.10 | katalanska | disdyakis triacontahedron | I h , [5,3], (*532) | 120 |  |
  
|
  
|
| 60 | V3 4 .5 | katalanska | femkantig hexecontahedron | I, [5,3] + , (532) | 60 |  |
||
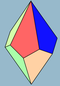
| 2 n | V3 3 . n | Polär |
asymmetrisk trapezhedron |
D n d , [2 + ,2 n ], (2* n ) D n , [2, n ] + , (22 n ) |
4 n 2 n |
|
||
|
2 n 4 n |
V4 2 . n V4 2 .2 n V4 2 .2 n |
Polär |
vanlig n - bipyramid isotoxal 2 n - bipyramid 2 n - scalenohedron |
D n h , [2, n ], (*22 n ) D n h , [2, n ], (*22 n ) D n d , [2 + ,2 n ], (2* n ) |
4 n |
  
|
   
|
k -isohedrisk figur
En polyeder (eller polytop i allmänhet) är k -isoedrisk om den innehåller k ytor inom sina fundamentala symmetridomäner. På liknande sätt har en k -isohedrisk plattsättning k separata symmetribanor (den kan innehålla m olika ansiktsformer, för m = k , eller bara för några m < k ). ("1-isohedral" är detsamma som "isohedral".)
En monohedrisk polyeder eller monohedrisk plattsättning ( m = 1) har kongruenta ytor, antingen direkt eller reflekterande, som förekommer i en eller flera symmetripositioner. En m -hedrisk polyeder eller plattsättning har m olika ansiktsformer (" dihedral ", " trihedral "... är samma som "2-hedral", "3-hedral"... respektive).
Här är några exempel på k -isoedriska polyedrar och plattsättningar, med deras ansikten färgade av deras k symmetripositioner:
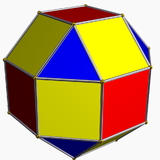
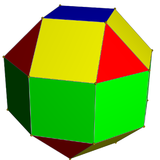
| 3-isohedral | 4-isohedral | isoedrisk | 2-isohedral |
|---|---|---|---|
| 2-hedriska polyedrar med regelbunden ansikte | Monoedriska polyedrar | ||
|
|
|
|
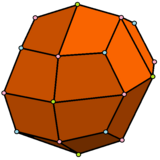
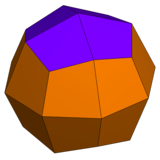
| Rombikuboktaedern har 1 triangeltyp och 2 kvadratiska typer . | Pseudo -rhombicuboctahedronen har 1 triangeltyp och 3 kvadratiska typer. | Den deltoidala icositetraedern har 1 ansiktstyp. | Den pseudo-deltoidala icositetrahedronen har 2 ansiktstyper, med samma form. |
| 2-isohedral | 4-isohedral | Isohedral | 3-isohedral |
|---|---|---|---|
| 2-hedriska kakelplattor med vanlig ansikte | Monoedriska plattor | ||

|

|

|
|
| Pythagoras plattsättning har 2 kvadratiska typer (storlekar). | Denna 3-enhetliga plattsättning har 3 triangeltyper, med samma form, och 1 kvadratisk typ. | Fiskbensmönstret har 1 rektangeltyp . | Denna femkantiga plattsättning har 3 oregelbundna pentagontyper, med samma form. |
Relaterade termer
En celltransitiv eller isokorisk figur är en n - polytop ( n ≥ 4) eller n - honungskaka ( n ≥ 3) som har sina celler kongruenta och transitiva med varandra. I 3 dimensioner är de katoptriska bikakorna , dubbla till de enhetliga bikakorna, isokoriska. I 4 dimensioner har isokora polytoper räknats upp till 20 celler.
En facetttransitiv eller isotopfigur är en n -dimensionell polytop eller bikaka med dess fasetter (( n −1)- ansikten ) kongruenta och transitiva. Dualen av en isotop är en isogonal polytop . Per definition är denna isotopegenskap gemensam för dualerna av de enhetliga polytoperna .
- En isotopisk 2-dimensionell figur är isotoxal, dvs kanttransitiv.
- En isotopisk 3-dimensionell figur är isoedrisk, dvs ansiktstransitiv.
- En isotop 4-dimensionell figur är isokorisk, dvs celltransitiv.
Se även
externa länkar
- Olshevsky, George. "Isotop" . Ordlista för Hyperspace . Arkiverad från originalet den 4 februari 2007.
- Weisstein, Eric W. "Isohedral plattsättning" . MathWorld .
- Weisstein, Eric W. "Isohedron" . MathWorld .
- isohedra 25 klasser av isoedrar med ett begränsat antal sidor
- Dice Design på The Dice Lab



