5-demikub

Demipenteract (5-demikub)
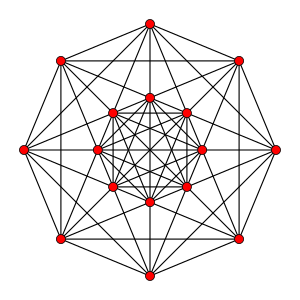Petrie- polygonprojektion
Typ	Uniform 5-polytop
Familj (D n )	5- demikub
Familjer (E n )	k 21 polytop 1 k2 polytop
Coxeter symbol	1 21
Schläfli symboler	{3,3 2,1 } = h{4,3 3 } s{2,4,3,3} eller h{2}h{4,3,3} sr{2,2,4,3} eller h{2}h{2}h{4,3} h{2}h{2}h{2}h{4} s{2 1,1,1,1 } eller h{2}h{2} h{2}s{2}
Coxeter diagram	=
4-ansikten	26	10 {3 1,1,1 } 16 {3,3,3}
Celler	120	40 {3 1,0,1 } 80 {3,3}
Ansikten	160	{3}
Kanter	80
Vertices	16
Vertex figur	korrigerad 5-cell
Petrie polygon	Oktogon
Symmetri	D 5 , [3 2,1,1 ] = [1 + ,4,3 3 ] [2 4 ] +
Egenskaper	konvex

I femdimensionell geometri är en demipenteract eller 5-demicube en semiregular 5-polytop , konstruerad av en 5-hypercube ( penteract ) med alternerade hörn borttagna.

Den upptäcktes av Thorold Gosset . Eftersom det var den enda halvregelbundna 5-polytopen (gjord av mer än en typ av vanliga fasetter ), kallade han den en 5-ic semi-regular . EL Elte identifierade den 1912 som en halvregelbunden polytop, märkte den som HM ₅ för en 5-dimensionell halvmåtts polytop.

Coxeter namngav denna polytop som 1 ₂₁ från dess Coxeter-diagram , som har grenar av längden 2, 1 och 1 med en ringad nod på en av de korta grenarna, och Schläfli-symbolen $\left\{ 3{\begin{array}{l}3,3\\3\end{array}}\right\}$ eller {3,3 ^2,1 }.

Den finns i k ₂₁ -polytopfamiljen som 1 ₂₁ med Gosset-polytoperna: 2 ₂₁ , 3 ₂₁ , och 4 ₂₁ .

Grafen som bildas av demipenteraktens hörn och kanter kallas ibland Clebsch-grafen , även om det namnet ibland syftar på den vikta kubgrafen av ordning fem istället.

kartesiska koordinater

Kartesiska koordinater för hörn av en demipenterakt centrerad vid origo och kantlängd 2 √ 2 är alternerande halvor av penterakten :

(±1,±1,±1,±1,±1)

med ett udda antal plustecken.

Som en konfiguration

Denna konfigurationsmatris representerar 5-demikuben. Raderna och kolumnerna motsvarar hörn, kanter, ytor, celler och 4-ytor. Diagonaltalen säger hur många av varje element som förekommer i hela 5-demikuben. De icke-diagonala talen säger hur många av kolumnens element som förekommer i eller vid radens element.

De diagonala f-vektortalen härleds genom Wythoff-konstruktionen , som dividerar hela gruppordningen för en undergruppsordning genom att ta bort en spegel åt gången.

D 5		k-ansikte	f k	f0	f 1	f 2	f 3		f 4		k -figur	anteckningar
A 4		( )	f0	16	10	30	10	20	5	5	korrigerad 5-cell	D5 /A4 = 16*5!/5 ! = 16
A 2 A 1 A 1		{ }	f 1	2	80	6	3	6	3	2	trekantsprisma	D 5 /A 2 A 1 A 1 = 16*5!/3!/2/2 = 80
A 2 A 1		{3}	f 2	3	3	160	1	2	2	1	Likbent triangel	D5 /A2A1 = 16 * 5 ! / 3!/2 = 160
A 3 A 1		h{4,3}	f 3	4	6	4	40	*	2	0	{ }	D5 /A3A1 = 16 * 5 ! / 4!/2 = 40
A 3		{3,3}		4	6	4	*	80	1	1	{ }	D5 /A3 = 16*5!/4 ! = 80
D 4		h{4,3,3}	f 4	8	24	32	8	8	10	*	( )	D 5 /D 4 = 16*5!/8/4! = 10
A 4		{3,3,3}		5	10	10	0	5	*	16	( )	D5 /A4 = 16*5!/5 ! = 16

* =

Projicerade bilder

Perspektivprojektion .

Bilder

ortografiska projektioner

Coxeter plan	B 5
Graf
Dihedral symmetri	[10/2]
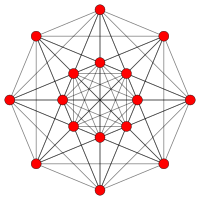
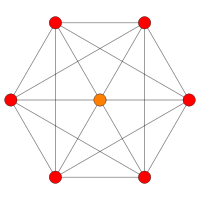
Coxeter plan	D 5	D 4
Graf
Dihedral symmetri	[8]	[6]
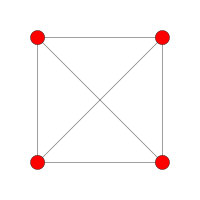
Coxeter plan	D 3	A 3
Graf
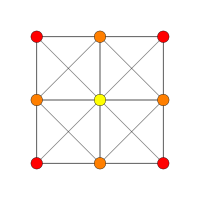
Dihedral symmetri	[4]	[4]

Besläktade polytoper

Det är en del av en dimensionell familj av enhetliga polytoper som kallas demihyperkuber för att vara alternerande av hyperkubfamiljen .

Det finns 23 enhetliga 5-polytoper (uniforma 5-polytoper) som kan konstrueras från D ₅ -symmetrin hos demipenterakten, varav 8 är unika för denna familj, och 15 delas inom den penteraktiska familjen.

5-demikuben är tredje i en dimensionell serie av halvregelbundna polytoper . Varje progressiv enhetlig polytop är konstruerad vertexfigur av den föregående polytopen. Thorold Gosset identifierade denna serie 1900 som innehållande alla vanliga polytopfasetter , innehållande alla simplexer och ortoplexer ( 5-simplicerade och 5-ortoplexer i fallet med 5-demikuben). I Coxeters notation ges 5-demikuben symbolen 1 ₂₁ .

k 21 figurer i n dimensionell
Plats	Ändlig						euklidisk	Hyperbolisk
E n	3	4	5	6	7	8	9	10
Coxeter grupp	E3 = A2A1 _ _ _	E4 = A4 _	E5 = D 5	E 6	E 7	E 8	E 9 = ${\tilde {E}}_{8}$ = E 8 +	E 10 = ${\bar {T}}_{8}$ = E 8 ++
Coxeter diagram
Symmetri	[3 −1,2,1 ]	[3 0,2,1 ]	[3 1,2,1 ]	[3 2,2,1 ]	[3 3,2,1 ]	[3 4,2,1 ]	[3 5,2,1 ]	[3 6,2,1 ]
Beställa	12	120	1 920	51,840	2,903,040	696,729,600	∞
Graf							-	-
namn	−1 21	021	1 21	2 21	3 21	4 21	5 21	6 21

1 k2 figurer i n dimensioner
Plats	Ändlig						euklidisk	Hyperbolisk
n	3	4	5	6	7	8	9	10
Coxeter grupp	E3 = A2A1 _ _ _	E4 = A4 _	E5 = D 5	E 6	E 7	E 8	E 9 = ${\tilde {E}}_{8}$ = E 8 +	E 10 = ${\bar {T}}_{8}$ = E 8 ++
Coxeter diagram
Symmetri (ordning)	[3 −1,2,1 ]	[3 0,2,1 ]	[3 1,2,1 ]	[[3 2,2,1 ]]	[3 3,2,1 ]	[3 4,2,1 ]	[3 5,2,1 ]	[3 6,2,1 ]
Beställa	12	120	1 920	103,680	2,903,040	696,729,600	∞
Graf							-	-
namn	1 −1,2	1 02	1 12	1 22	1 32	1 42	1 52	1 62

• T. Gosset : On the Regular and Semi-Regular Figures in Space of n Dimensions , Messenger of Mathematics , Macmillan, 1900
• HSM Coxeter :
  •   Coxeter, Regular Polytopes , (3:e upplagan, 1973), Dover-upplagan, ISBN 0-486-61480-8 , sid. 296, Tabell I (iii): Regelbundna polytoper, tre vanliga polytoper i n-dimensioner (n≥5)
  • HSM Coxeter, Regular Polytopes , 3:e upplagan, Dover New York, 1973, sid. 296, Tabell I (iii): Regelbundna polytoper, tre vanliga polytoper i n-dimensioner (n≥5)
  •   Kaleidoscopes: Selected Writings of HSM Coxeter , redigerad av F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
    • (Papper 22) HSM Coxeter, Regular and Semi Regular Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Papper 23) HSM Coxeter, Regular and Semi-Regular Polytopes II , [Math. Zeit. 188 (1985) 559-591]
    • (Papper 24) HSM Coxeter, Regular and Semi-Regular Polytopes III , [Math. Zeit. 200 (1988) 3-45]
•   John H. Conway , Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (kapitel 26. s. 409: Hemicubes: 1 _n1 )
• Klitzing, Richard. "5D enhetliga polytoper (polytera) x3o3o *b3o3o - hin" .

externa länkar

• Olshevsky, George. "Demipenteract" . Ordlista för Hyperspace . Arkiverad från originalet den 4 februari 2007.
• Flerdimensionell ordlista