Kvarts hyperkubisk honungskaka

I geometri är den fjärdedels hyperkubiska honeycomb (eller fjärdedel n-cubic honeycomb ) en dimensionell oändlig serie av honeycombs , baserad på den hypercube honeycomb . Den ges en Schläfli-symbol q{4,3...3,4} eller Coxeter-symbol qδ ₄ som representerar den reguljära formen med tre fjärdedelar av hörnen borttagna och innehåller symmetrin för Coxeter-gruppen ${ \tilde {D}}_{n-1}$ för n ≥ 5, med ${\tilde {D}}_{4}$ = ${\tilde {A} }_{4}$ och för kvarts n-kubiska bikakor ${\tilde {D}}_{5}$ = ${\tilde {B}}_{5}$ .

qδ n	namn	Schläfli symbol	Coxeter diagram	Fasetter			Vertex figur
qδ 3	kvarts kvadratisk plattsättning	q{4,4}	eller eller	h{4}={2}	{ }×{ }		{ }×{ }
qδ 4	kvarts kubisk honungskaka	q{4,3,4}	eller eller	h{4,3}	h 2 {4,3}		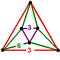Förlängd triangulär antiprisma
qδ 5	kvarts tesseractic honeycomb	q{4,3 2 ,4}	eller eller	h{4,3 2 }	h 3 {4,3 2 }		{3,4}×{}
qδ 6	kvarts 5-kubiks honungskaka	q{4,3 3 ,4}		h{4,3 3 }	h 4 {4,3 3 }		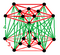Rättad 5-cells antiprisma
qδ 7	fjärdedels 6-kubiks honungskaka	q{4,3 4,4 }		h{4,3 4 }	h 5 {4,3 4 }	{3,3}×{3,3}
qδ 8	kvart 7-kubik honungskaka	q{4,3 5,4 }		h{4,3 5 }	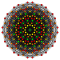h 6 {4,3 5 }	{3,3}×{3,3 1,1 }
qδ 9	kvarts 8-kubiks honungskaka	q{4,3 6 ,4}		h{4,3 6 }	h7{4,36}	{3,3}×{3,3 2,1 } {3,3 1,1 }×{3,3 1,1 }
qδ n	kvarts n-kubisk honungskaka	q{4,3 n-3 ,4}	...	h{4,3 n-2 }	h n-2 {4,3 n-2 }	...

Se även

• Hyperkubisk honungskaka
• Alternerad hyperkubisk honungskaka
• Enkel bikaka
• Stympad simplektisk honungskaka
• Omnitruncated simplectic honeycomb

•   Coxeter, HSM Regular Polytopes , (3:e upplagan, 1973), Dover-upplagan, ISBN 0-486-61480-8
  1. s. 122–123, 1973. (Gallret av hyperkuber γ _n bildar de kubiska bikakorna , δ _n+1 )
  2. s. 154–156: Partiell trunkering eller alternering, representerad av q- prefix
  3. sid. 296, Tabell II: Vanliga bikakor, δ _n+1
•   Kaleidoscopes: Selected Writings of HSM Coxeter , redigerad av F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  • (Papper 22) HSM Coxeter, Regular and Semi Regular Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Enhetliga utrymmesfyllningar)
  • (Papper 24) HSM Coxeter, Regular and Semi-Regular Polytopes III , [Math. Zeit. 200 (1988) 3-45] Se sid 318 [2]
• Klitzing, Richard. "1D-8D euklidiska tesselationer" .

Grundläggande konvexa regelbundna och enhetliga bikakor i dimensionerna 2–9
Plats	Familj	${\tilde {A}}_{n-1}$	${\tilde {C}}_{n-1}$	${\tilde {B}}_{n-1}$	${\tilde {D}}_{n-1}$	${\tilde {G}}_{2}$ / ${\tilde {F}}_{4}$ / ${\tilde { E}}_{n-1}$
E 2	Enhetlig plattsättning	{3 [3] }	δ 3	hδ 3	qδ 3	Hexagonal
E 3	Enhetlig konvex bikaka	{3 [4] }	δ 4	hδ 4	qδ 4
E 4	Uniform 4-honeycomb	{3 [5] }	δ 5	hδ 5	qδ 5	24-cells honungskaka
E 5	Uniform 5-bikaka	{3 [6] }	δ 6	hδ 6	qδ 6
E 6	Uniform 6-honeycomb	{3 [7] }	δ 7	hδ 7	qδ 7	2 22
E 7	Uniform 7-honeycomb	{3 [8] }	δ 8	hδ 8	qδ 8	1 33 • 3 31
E 8	Uniform 8-honeycomb	{3 [9] }	δ 9	hδ 9	qδ 9	1 52 • 2 51 • 5 21
E 9	Uniform 9-honeycomb	{3 [10] }	δ 10	hδ 10	qδ 10
E 10	Uniform 10-honeycomb	{3 [11] }	δ 11	hδ 11	qδ 11
E n -1	Uniform ( n -1)- honeycomb	{3 [n] }	5 n	hδ n	qδ n	1 k2 • 2 k1 • k 21