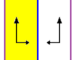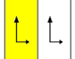Lista över plana symmetrigrupper

Den här artikeln sammanfattar klasserna av diskreta symmetrigrupper på det euklidiska planet . Symmetrigrupperna namnges här med tre namnscheman: Internationell notation , orbifold notation och Coxeter notation . Det finns tre typer av symmetrigrupper i planet:

• 2 familjer av rosettgrupper – 2D- punktgrupper
• 7 frisgrupper – 2D linjegrupper
• 17 tapetgrupper – 2D rymdgrupper .

Rosettgrupper

Det finns två familjer av diskreta tvådimensionella punktgrupper, och de specificeras med parametern n , som är ordningen för gruppen av rotationer i gruppen.

Familj	Intl ( orbifold )	Schön.	Geo Coxeter	Beställa	Exempel
Cyklisk symmetri	n (n•)	C n	n [n] +	n	C 1 , [ ] + (•)	C2 , [2] + (2• )	C3 , [3] + (3• )	C4 , [4] + (4• )	C5 , [5] + (5• )	C6 , [6] + (6• )
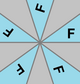
Dihedral symmetri	n m (*n•)	D n	n [n]	2 n	D 1 , [ ] (*•)	D 2 , [2] (*2•)	D 3 , [3] (*3•)	D 4 , [4] (*4•)	D 5 , [5] (*5•)	D 6 , [6] (*6•)

Frisgrupper

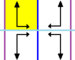
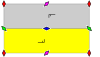
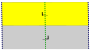
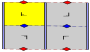
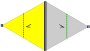
De 7 frisgrupperna , de tvådimensionella linjegrupperna , med en periodicitetsriktning ges med fem notationsnamn. Schönflies notation ges som oändliga gränser för 7 dihedriska grupper. De gula områdena representerar den oändliga fundamentala domänen i varje.

[1,∞], IUC ( orbifold ) Geo Schönflies Coxeter Grundläggande domän Exempel p1m1 (*∞•) p1 C ∞v [1,∞] sidle p1 (∞•) p 1 C ∞ [1,∞] + hopp [2,∞ + ], IUC (orbifold) Geo Schönflies Coxeter Grundläggande domän Exempel p11m (∞*) sid. 1 C ∞h [2,∞ + ] hoppa p11g (∞×) sid. g 1 S 2∞ [2 + ,∞ + ] steg

[2,∞], IUC (orbifold) Geo Schönflies Coxeter Grundläggande domän Exempel p2mm (*22∞) p2 D ∞h [2,∞] snurrande hopp p2mg (2*∞) p2 g D ∞d [2 + ,∞] snurrande sida p2 (22∞) p 2 D ∞ [2,∞] + snurrande humle

Bakgrundsgrupper

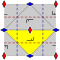
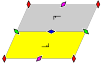
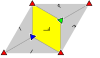
De 17 tapetgrupperna , med ändliga fundamentala domäner, ges av internationell notation , orbifold notation och Coxeter notation , klassificerade av de 5 Bravais-gittren i planet: kvadratisk , snedställd (parallelogrammatisk), hexagonal (liksidig triangulär), rektangulär (centrerad rombisk ) och rombisk (centrerad rektangulär).

Pl- och p2 -grupperna, utan reflektionssymmetri, upprepas i alla klasser . Den relaterade rena reflekterande Coxeter-gruppen ges med alla klasser utom sned.

Fyrkant [4,4], IUC ( Orb. ) Geo Coxeter Domän Conway namn p1 (°) p 1 Monotropisk s2 (2222) s 2 [4,1 + ,4] + [1 + ,4,4,1 + ] + Ditropiskt pgg (22×) p g 2 g [4 + ,4 + ] Diglide pmm (*2222) s2 [4,1 + ,4] [1 + ,4,4,1 + ] Diskopisk cmm (2*22) c2 [(4,4,2 + )] Dirhombic s4 (442) s 4 [4,4] + Tetratropisk p4g (4*2) sid g 4 [4 + ,4] Tetragyro p4m (*442) p4 [4,4] Tetraskopisk

Rektangulär [∞ h ,2,∞ v ], IUC (Orb.) Geo Coxeter Domän Conway namn p1 (°) p 1 [∞ + ,2,∞ + ] Monotropisk s2 (2222) s 2 [∞,2,∞] + Ditropiskt pg(h) (××) p g 1 h: [∞ + ,(2,∞) + ] Monoglid pg(v) (×× ) pg 1 v: [(∞,2) + ,∞ + ] Monoglid pgm (22*) sid g 2 h: [(∞,2) + ,∞] Digyro pmg (22*) sid g 2 v: [∞,(2,∞) + ] Digyro pm(h) (**) p1 h: [∞ + ,2,∞] Monoskopisk pm(v) (**) p1 v: [∞,2,∞ + ] Monoskopisk pmm (*2222) s2 [∞,2,∞] Diskopisk

Rombisk [∞ h ,2 + ,∞ v ], IUC (Orb.) Geo Coxeter Domän Conway namn p1 (°) p 1 [∞ + ,2 + ,∞ + ] Monotropisk s2 (2222) s 2 [∞,2 + ,∞] + Ditropiskt cm(h) (*×) cl h: [∞ + ,2 + ,∞] Monorhombisk cm(v) (*×) cl v: [∞,2 + ,∞ + ] Monorhombisk pgg (22×) p g 2 g [((∞,2) + ) [2] ] Diglide cmm (2*22) c2 [∞,2 + ,∞] Dirhombic Parallelogrammatisk ( snett ) p1 (°) p 1 Monotropisk s2 (2222) s 2 Ditropiskt

Hexagonal /Triangulär [6,3], / [3 [3] ], IUC (Orb.) Geo Coxeter Domän Conway namn p1 (°) p 1 Monotropisk s2 (2222) s 2 [6,3] Δ Ditropiskt cmm (2*22) c2 [6,3] ⅄ Dirhombic s3 (333) s 3 [1 + ,6,3 + ] [3 [3] ] + Tritropisk p3m1 (*333) p3 [1 + ,6,3] [3 [3] ] Triskopisk p31m (3*3) h3 [6,3 + ] Trigyro s6 (632) s 6 [6,3] + Hexatropisk p6m (*632) p6 [6,3] Hexaskopisk

Tapetundergruppsrelationer

Undergruppsrelationer bland de 17 tapetgruppen

		o	2222	××	**	*×	22×	22*	*2222	2*22	442	4*2	*442	333	*333	3*3	632	*632
		p1	p2	sid	kl	centimeter	pgg	pmg	pmm	cmm	p4	p4g	p4m	p3	p3m1	p31m	s6	p6m
o	p1	2
2222	p2	2	2	2
××	sid	2		2
**	kl	2		2	2	2
*×	centimeter	2		2	2	3
22×	pgg	4	2	2			3
22*	pmg	4	2	2	2	4	2	3
*2222	pmm	4	2	4	2	4	4	2	2	2
2*22	cmm	4	2	4	4	2	2	2	2	4
442	p4	4	2								2
4*2	p4g	8	4	4	8	4	2	4	4	2	2	9
*442	p4m	8	4	8	4	4	4	4	2	2	2	2	2
333	p3	3												3
*333	p3m1	6		6	6	3								2	4	3
3*3	p31m	6		6	6	3								2	3	4
632	s6	6	3											2			4
*632	p6m	12	6	12	12	6	6	6	6	3				4	2	2	2	3

Se även

• Lista över sfäriska symmetrigrupper
• Orbifold notation#Hyperboliskt plan - Hyperboliska symmetrigrupper

Anteckningar

•   The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, ISBN 978-1-56881-220-5 (Orbifold notation for polyhedra, Euclidean and hyperbolic platting)
•   On Quaternions and Octonions , 2003, John Horton Conway och Derek A. Smith ISBN 978-1-56881-134-5
•   Kaleidoscopes: Selected Writings of HSM Coxeter , redigerad av F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [2]
  • (Papper 22) HSM Coxeter, Regular and Semi Regular Polytopes I , [Math. Zeit. 46 (1940) 380–407, MR 2,10]
  • (Papper 23) HSM Coxeter, Regular and Semi-Regular Polytopes II , [Math. Zeit. 188 (1985) 559–591]
  • (Papper 24) HSM Coxeter, Regular and Semi-Regular Polytopes III , [Math. Zeit. 200 (1988) 3–45]
•   Coxeter, HSM & Moser, WOJ (1980). Generatorer och relationer för diskreta grupper . New York: Springer-Verlag. ISBN 0-387-09212-9 .
•   NW Johnson : Geometries and Transformations , (2018) ISBN 978-1-107-10340-5 Kapitel 12: Euklidiska symmetrigrupper

externa länkar

• "Conways manuskript" på Orbifold-notation (notation ändrad från detta original, x används nu i stället för öppen punkt och o används i stället för den stängda punkten)
• De 17 tapetgrupperna