Genetisk drift

Ej att förväxla med genetiskt utkast , antigendrift eller antigenskifte .

Genetisk drift , även känd som alleldrift eller Wright-effekten , är förändringen i frekvensen av en existerande genvariant ( allel ) i en population på grund av en slumpmässig slump.

Genetisk drift kan göra att genvarianter försvinner helt och därmed minska genetisk variation . Det kan också orsaka att initialt sällsynta alleler blir mycket mer frekventa och till och med fixerade.

När det finns få kopior av en allel är effekten av genetisk drift mer anmärkningsvärd, och när många kopior finns är effekten mindre anmärkningsvärd. I mitten av 1900-talet uppstod livliga debatter om den relativa betydelsen av naturligt urval kontra neutrala processer, inklusive genetisk drift. Ronald Fisher , som förklarade naturligt urval med hjälp av Mendelsk genetik , hade åsikten att genetisk drift spelar på sin höjd en mindre roll i evolutionen , och detta förblev den dominerande uppfattningen i flera decennier. 1968 återuppväckte befolkningsgenetikern Motoo Kimura debatten med sin neutrala teori om molekylär evolution , som hävdar att de flesta fall där en genetisk förändring sprider sig över en population (även om det inte nödvändigtvis är förändringar i fenotyper ) orsakas av genetisk drift som verkar på neutrala mutationer . På 1990-talet föreslogs konstruktiv neutral evolution som försöker förklara hur komplexa system uppstår genom neutrala övergångar.

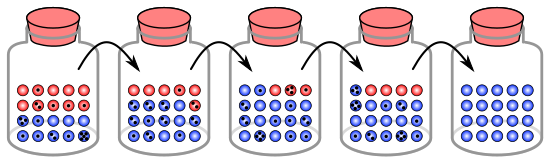
Analogi med kulor i en burk

Processen med genetisk drift kan illustreras med hjälp av 20 kulor i en burk för att representera 20 organismer i en population. Betrakta denna burk med kulor som startpopulationen. Hälften av kulorna i burken är röda och hälften är blå, där varje färg motsvarar en annan allel av en gen i populationen. I varje ny generation förökar sig organismerna slumpmässigt. För att representera denna reproduktion, välj slumpmässigt en kula från originalburken och lägg en ny kula med samma färg i en ny burk. Detta är "avkommorna" till den ursprungliga marmorn, vilket betyder att den ursprungliga marmorn finns kvar i sin burk. Upprepa denna process tills det finns 20 nya kulor i den andra burken. Den andra burken kommer nu att innehålla 20 "avkommor", eller kulor i olika färger. Om inte den andra burken innehåller exakt 10 röda kulor och 10 blå kulor, har en slumpmässig förskjutning inträffat i allelfrekvenserna.

Om denna process upprepas ett antal gånger, fluktuerar antalet röda och blå kulor som plockas varje generation. Ibland har en burk fler röda kulor än sin "förälder" burk och ibland mer blå. Denna fluktuation är analog med genetisk drift – en förändring i populationens allelfrekvens som beror på en slumpmässig variation i fördelningen av alleler från en generation till nästa.

I en generation kunde inga kulor av en viss färg väljas, vilket betyder att de inte har någon avkomma. I det här exemplet, om inga röda kulor väljs, innehåller burken som representerar den nya generationen endast blå avkomma. Om detta händer har den röda allelen förlorats permanent i befolkningen, medan den återstående blå allelen har fixerats: alla framtida generationer är helt blå. I små populationer fixering ske på bara några få generationer.

I denna simulering betyder varje svart prick på en kula att den har valts för kopiering (reproduktion) en gång. Fixering i den blå "allelen" sker inom fem generationer.

Sannolikhet och allelfrekvens

Mekanismerna för genetisk drift kan illustreras med ett förenklat exempel. Betrakta en mycket stor koloni av bakterier isolerade i en droppe lösning. Bakterierna är genetiskt identiska förutom en enda gen med två alleler märkta A och B , som är neutrala alleler, vilket betyder att de inte påverkar bakteriernas förmåga att överleva och föröka sig; alla bakterier i denna koloni är lika sannolikt att överleva och föröka sig. Anta att hälften av bakterierna har allel A och den andra hälften har allel B . Således A och B vardera en allelfrekvens på 1/2.

Droppen av lösningen krymper sedan tills den bara har tillräckligt med mat för att upprätthålla fyra bakterier. Alla andra bakterier dör utan att föröka sig. Bland de fyra som överlever finns 16 möjliga kombinationer för A- och B -allelerna: (AAAA), (BAAA), (ABAA), (BBAA), ( AABA), (BABA), (ABBA), (BBBA), ( AAAB), (BAAB), (ABAB), (BBAB), (AABB), (BABB), (ABBB), (BBBB).

Eftersom alla bakterier i den ursprungliga lösningen är lika sannolikt att överleva när lösningen krymper, är de fyra överlevande ett slumpmässigt prov från den ursprungliga kolonin. Sannolikheten är 1/2, så sannolikheten för att någon speciell allelkombination inträffar när lösningen krymper är

${\frac {1}{2}}\cdot {\frac {1}{2}}\cdot {\frac {1}{2}}\cdot {\frac {1}{2}}= {\frac {1}{16}}.$

(Den ursprungliga populationsstorleken är så stor att provtagningen faktiskt sker med utbyte). Med andra ord är var och en av de 16 möjliga allelkombinationerna lika sannolikt att inträffa, med sannolikhet 1/16.

Att räkna kombinationerna med samma antal A och B ger följande tabell:

A	B	Kombinationer	Sannolikhet
4	0	1	1/16
3	1	4	16/4
2	2	6	16/6
1	3	4	16/4
0	4	1	1/16

Som visas i tabellen är det totala antalet kombinationer som har samma antal A -alleler som B -alleler sex, och sannolikheten för denna kombination är 6/16. Det totala antalet andra kombinationer är tio, så sannolikheten för ojämnt antal A- och B -alleler är 10/16. Således, även om den ursprungliga kolonin började med lika många A- och B -alleler, kommer antalet alleler i den återstående populationen av fyra medlemmar mycket möjligt inte att vara lika. Situationen med lika siffror är faktiskt mindre sannolik än ojämna siffror. I det senare fallet har genetisk drift skett på grund av att populationens allelfrekvenser har förändrats på grund av slumpmässig provtagning. I det här exemplet minskade befolkningen till bara fyra slumpmässiga överlevande, ett fenomen som kallas en befolkningsflaskhals .

Sannolikheterna för antalet kopior av allel A (eller B ) som överlever (givna i den sista kolumnen i tabellen ovan) kan beräknas direkt från binomialfördelningen , där sannolikheten för "framgång" (sannolikheten för att en given allel är närvarande ) är 1/2 (dvs sannolikheten att det finns k kopior av A (eller B ) alleler i kombinationen) ges av:

${n \choose k}\left({\frac {1}{2}} \right)^{k}\left(1-{\frac {1}{2}}\right)^{nk}={n \välj k}\left({\frac {1}{2}}\ höger)^{n}\!$

där n=4 är antalet överlevande bakterier.

Matematiska modeller

Matematiska modeller av genetisk drift kan utformas med antingen förgreningsprocesser eller en diffusionsekvation som beskriver förändringar i allelfrekvens i en idealiserad population .

Wright–Fisher modell

Betrakta en gen med två alleler, A eller B . I diploidy har populationer som består av N individer 2 N kopior av varje gen. En individ kan ha två kopior av samma allel eller två olika alleler. Frekvensen för en allel tilldelas p och den andra q . Wright–Fisher-modellen (uppkallad efter Sewall Wright och Ronald Fisher ) antar att generationer inte överlappar varandra (till exempel har ettåriga växter exakt en generation per år) och att varje kopia av genen som finns i den nya generationen ritas slumpmässigt oberoende av varandra. från alla kopior av genen i den gamla generationen. Formeln för att beräkna sannolikheten att få k kopior av en allel som hade frekvensen p i den senaste generationen är då

${\frac {(2N)!}{k!(2N-k)!}}p^{k}q^{2N-k}$

där symbolen " ! " betecknar den faktoriella funktionen. Detta uttryck kan också formuleras med hjälp av binomialkoefficienten ,

${2N \choose k}p^{k}q^{2N-k}$

Moran modell

Moran -modellen utgår från överlappande generationer. Vid varje tidssteg väljs en individ att fortplanta sig och en individ väljs att dö. Så i varje tidssteg kan antalet kopior av en given allel öka med en, gå ner med en eller förbli densamma. Det betyder att övergångsmatrisen är tridiagonal , vilket innebär att matematiska lösningar är lättare för Moran-modellen än för Wright–Fisher-modellen. Å andra sidan datorsimuleringar vanligtvis lättare att utföra med Wright–Fisher-modellen, eftersom färre tidssteg behöver beräknas. I Moran-modellen tar det N tidssteg för att ta sig igenom en generation, där N är den effektiva populationsstorleken . I Wright–Fisher-modellen krävs bara en.

I praktiken ger Moran- och Wright–Fisher-modellerna kvalitativt liknande resultat, men genetisk drift går dubbelt så snabbt i Moran-modellen.

Andra modeller av drift

Om variansen i antalet avkommor är mycket större än den som ges av den binomialfördelning som antas av Wright-Fisher-modellen, är genetisk drift en mindre kraftfull kraft, givet samma totala hastighet av genetisk drift (variansens effektiva populationsstorlek). jämfört med urval. Även för samma varians, om högre moment av avkommantalsfördelningen överstiger de för binomialfördelningen, så försvagas återigen kraften av genetisk drift avsevärt.

Andra slumpmässiga effekter än provtagningsfel

Slumpmässiga förändringar i allelfrekvenser kan också orsakas av andra effekter än samplingsfel , till exempel slumpmässiga förändringar i urvalstrycket.

En viktig alternativ källa till stokasticitet , kanske viktigare än genetisk drift, är genetisk utkast . Genetisk utkast är effekten på ett lokus genom urval på länkade lokus. De matematiska egenskaperna hos genetiskt utkast skiljer sig från genetisk drift. Riktningen för den slumpmässiga förändringen i allelfrekvens är autokorrelerad över generationer.

Drift och fixering

Hardy -Weinberg-principen säger att inom tillräckligt stora populationer förblir allelfrekvenserna konstanta från en generation till nästa om inte jämvikten störs av migration , genetiska mutationer eller urval .

I ändliga populationer erhålls dock inga nya alleler från det slumpmässiga urvalet av alleler som skickas till nästa generation, men provtagningen kan få en befintlig allel att försvinna. Eftersom slumpmässig provtagning kan ta bort, men inte ersätta, en allel, och eftersom slumpmässiga minskningar eller ökningar av allelfrekvens påverkar förväntade allelfördelningar för nästa generation, driver genetisk drift en population mot genetisk enhetlighet över tid. När en allel når en frekvens på 1 (100%) sägs den vara "fixerad" i populationen och när en allel når en frekvens på 0 (0%) går den förlorad. Mindre populationer uppnår fixering snabbare, medan fixering inte uppnås inom gränsen för en oändlig population. När en allel väl har fixerats stannar den genetiska driften och allelfrekvensen kan inte ändras om inte en ny allel introduceras i populationen via mutation eller genflöde . Även om genetisk drift är en slumpmässig, riktningslös process, verkar den för att eliminera genetisk variation över tiden.

Frekvensförändring av allel på grund av drift

Tio simuleringar av slumpmässig genetisk drift av en enskild given allel med en initial frekvensfördelning på 0,5 uppmätt under loppet av 50 generationer, upprepade i tre reproduktivt synkrona populationer av olika storlekar. I dessa simuleringar driver alleler till förlust eller fixering (frekvens på 0,0 eller 1,0) endast i den minsta populationen.

Om man antar att genetisk drift är den enda evolutionära kraften som verkar på en allel, efter t generationer i många replikerade populationer, börjar med allelfrekvenserna p och q , är variansen i allelfrekvens över dessa populationer

$V_{t}\approx pq\left(1-\exp \left(-{\frac {t}{2N_{e} }}\eller hur)$

Dags för fixering eller förlust

Förutsatt att genetisk drift är den enda evolutionära kraften som verkar på en allel, vid varje given tidpunkt är sannolikheten att en allel så småningom kommer att fixeras i populationen helt enkelt dess frekvens i populationen vid den tiden. Till exempel, om frekvensen p för allel A är 75 % och frekvensen q för allel B är 25 %, då är sannolikheten för att A slutligen kommer att fixeras i populationen, givet obegränsad tid, 75 % och sannolikheten att B blir fixerad är 25 %.

Det förväntade antalet generationer för att fixering ska inträffa är proportionellt mot populationens storlek, så att fixering förutsägs inträffa mycket snabbare i mindre populationer. Normalt används den effektiva populationsstorleken, som är mindre än den totala populationen, för att bestämma dessa sannolikheter. Den effektiva populationen ( N _e ) tar hänsyn till faktorer som nivån av inavel , i vilket skede av livscykeln populationen är den minsta och det faktum att vissa neutrala gener är genetiskt kopplade till andra som är under urval. Den effektiva populationsstorleken kanske inte är densamma för varje gen i samma population.

En framåtblickande formel som används för att uppskatta den förväntade tiden innan en neutral allel fixeras genom genetisk drift, enligt Wright-Fisher-modellen, är

${\bar {T}}_{\text{fixed}}={\frac {-4N_{e}( 1-p)\ln(1-p)}{p}}$

där T är antalet generationer, Ne är den effektiva populationsstorleken och p är _den initiala frekvensen för den givna allelen. Resultatet är antalet generationer som förväntas gå innan fixering sker för en given allel i en population med given storlek ( _Ne ) och allelfrekvens ( p ).

Den förväntade tiden för den neutrala allelen att gå förlorad genom genetisk drift kan beräknas som

${\bar {T}}_{\text{lost}}={\frac {-4N_{e}p}{1-p}}\ln sid.$

När en mutation endast uppträder en gång i en population som är tillräckligt stor för att den initiala frekvensen ska vara försumbar, kan formlerna förenklas till

${\bar {T}}_{\text{fixed}}=4N_{e}$

för genomsnittligt antal generationer som förväntas före fixering av en neutral mutation, och

${\bar {T}}_{\text{lost}}=2\left({\frac {N_{e}}{N }}\right)\ln(2N)$

för det genomsnittliga antalet generationer som förväntas före förlusten av en neutral mutation i en population av verklig storlek N.

Dags att förlora med både drift och mutation

Formlerna ovan gäller för en allel som redan finns i en population, och som varken är föremål för mutation eller naturligt urval. Om en allel förloras genom mutation mycket oftare än vad den erhålls genom mutation, kan mutation, såväl som drift, påverka tiden till förlust. Om allelen som är benägen till mutationsförlust börjar som fixerad i populationen och går förlorad genom mutation med hastighet m per replikation, så ges den förväntade tiden i generationer till dess förlust i en haploid population av

${\bar {T}}_{\text{lost}}\approx {\begin{cases}{\dfrac {1}{m}},{\text{ if }}mN_{e}\ll 1\\[8pt]{\dfrac {\ln {(mN_{e})} +\gamma }{m}}{\text{ if }}mN_{e}\gg 1\end{case}}$

där $\gamma$ är Eulers konstant . Den första approximationen representerar väntetiden tills den första mutanten är avsedd för förlust, varvid förlusten då sker relativt snabbt genom genetisk drift, vilket tar tid 1 / m ≫ N _e . Den andra approximationen representerar den tid som behövs för deterministisk förlust genom mutationsackumulering. I båda fallen domineras tiden till fixering av mutation via termen 1 / m , och påverkas mindre av den effektiva populationsstorleken .

Mot naturligt urval

I naturliga populationer verkar genetisk drift och naturligt urval inte isolerat; båda fenomenen är alltid på gång, tillsammans med mutation och migration. Neutral evolution är produkten av både mutation och drift, inte av drift ensam. På samma sätt, även när selektion överväldigar genetisk drift, kan det bara verka på variation som mutation ger.

Medan det naturliga urvalet har en riktning som styr utvecklingen mot ärftliga anpassningar till den nuvarande miljön, har genetisk drift ingen riktning och styrs endast av slumpens matematik . Som ett resultat verkar drift på de genotypiska frekvenserna inom en population utan hänsyn till deras fenotypiska effekter. Däremot gynnar selektion spridningen av alleler vars fenotypiska effekter ökar överlevnaden och/eller reproduktionen av deras bärare, sänker frekvensen av alleler som orsakar ogynnsamma egenskaper och ignorerar de som är neutrala.

Lagen om stora siffror förutspår att när det absoluta antalet kopior av allelen är litet (t.ex. i små populationer ), är storleken på driften på allelfrekvenser per generation större. Storleken på driften är tillräckligt stor för att överväldiga selektion vid vilken allelfrekvens som helst när selektionskoefficienten är mindre än 1 dividerat med den effektiva populationsstorleken. Icke-adaptiv evolution som härrör från produkten av mutation och genetisk drift anses därför vara en följdmekanism för evolutionär förändring främst inom små, isolerade populationer. Matematiken för genetisk drift beror på den effektiva populationsstorleken, men det är inte klart hur detta är relaterat till det faktiska antalet individer i en population. Genetisk koppling till andra gener som är under selektion kan minska den effektiva populationsstorleken som upplevs av en neutral allel. Med en högre rekombinationshastighet minskar kopplingen och därmed denna lokala effekt på effektiv populationsstorlek. Denna effekt är synlig i molekylära data som en korrelation mellan lokal rekombinationshastighet och genetisk mångfald , och negativ korrelation mellan gentäthet och mångfald vid icke-kodande DNA- regioner. Stokasticitet förknippad med koppling till andra gener som är under urval är inte detsamma som provtagningsfel och kallas ibland genetiskt utkast för att skilja det från genetisk drift.

Låg allelfrekvens gör alleler mer känsliga för att elimineras av en slump, och till och med åsidosätter påverkan av naturligt urval. Till exempel, medan ofördelaktiga mutationer vanligtvis elimineras snabbt inom befolkningen, är nya fördelaktiga mutationer nästan lika känsliga för förlust genom genetisk drift som neutrala mutationer. Inte förrän allelfrekvensen för den fördelaktiga mutationen når en viss tröskel kommer genetisk drift inte att ha någon effekt.

Befolkningsflaskhals

Huvudartikel: Befolkningsflaskhals

Förändringar i en populations allelfrekvens efter en populationsflaskhals : den snabba och radikala nedgången i populationsstorlek har minskat populationens genetiska variation .

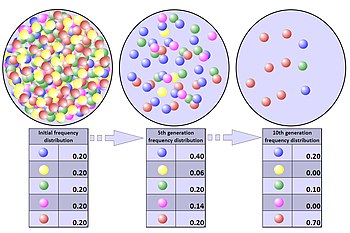
En befolkningsflaskhals är när en befolkning minskar till en betydligt mindre storlek under en kort tidsperiod på grund av någon slumpmässig miljöhändelse. I en sann befolkningsflaskhals är oddsen för överlevnad för någon medlem av befolkningen rent slumpmässigt och förbättras inte av någon speciell inneboende genetisk fördel. Flaskhalsen kan resultera i radikala förändringar i allelfrekvenser, helt oberoende av urval.

Effekten av en befolkningsflaskhals kan bibehållas, även när flaskhalsen orsakas av en engångshändelse som en naturkatastrof. Ett intressant exempel på en flaskhals som orsakar ovanlig genetisk distribution är den relativt höga andelen individer med total stavcellsfärgblindhet ( achromatopsia ) på Pingelap- atollen i Mikronesien . Efter en flaskhals ökar inaveln. Detta ökar skadan som orsakas av recessiva skadliga mutationer, i en process som kallas inavelsdepression . De värsta av dessa mutationer selekteras mot, vilket leder till förlust av andra alleler som är genetiskt kopplade till dem, i en process av bakgrundsselektion . För recessiva skadliga mutationer kan detta urval förbättras som en konsekvens av flaskhalsen, på grund av genetisk utrensning . Detta leder till en ytterligare förlust av genetisk mångfald. Dessutom ökar en varaktig minskning av populationsstorleken sannolikheten för ytterligare allelfluktuationer från drift under kommande generationer.

En populations genetiska variation kan reduceras avsevärt av en flaskhals, och även fördelaktiga anpassningar kan elimineras permanent. Förlusten av variation gör den överlevande befolkningen sårbar för alla nya selektionstryck såsom sjukdomar, klimatförändringar eller förändringar i den tillgängliga födokällan, eftersom anpassning som svar på miljöförändringar kräver tillräcklig genetisk variation i befolkningen för att naturligt urval ska kunna ske.

Det har förekommit många kända fall av befolkningsflaskhals på senare tid. Före européernas ankomst var nordamerikanska prärier livsmiljö för miljontals större präriehöns . Bara i Illinois rasade deras antal från cirka 100 miljoner fåglar år 1900 till cirka 50 fåglar på 1990-talet. Nedgången i populationen berodde på jakt och förstörelse av livsmiljöer, men en konsekvens har blivit en förlust av större delen av artens genetiska mångfald. DNA- analys som jämför fåglar från mitten av århundradet med fåglar på 1990-talet dokumenterar en kraftig nedgång i den genetiska variationen bara under de senaste decennierna. För närvarande upplever den större präriekycklingen låg reproduktionsframgång .

Den genetiska förlusten som orsakas av flaskhals och genetisk drift kan dock öka konditionen, som i Ehrlichia .

Överjakt orsakade också en allvarlig flaskhals hos den norra elefantsälen på 1800-talet. Deras resulterande nedgång i genetisk variation kan härledas genom att jämföra den med den för den sydliga elefantsälen, som inte jagades så aggressivt.

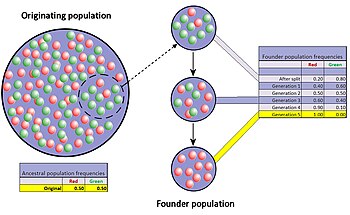
Grundareffekt

Huvudartikel: Grundareffekt

När mycket få medlemmar av en befolkning migrerar för att bilda en separat ny befolkning uppstår grundareffekten. Under en period efter grundandet upplever den lilla befolkningen intensiv drift. I figuren resulterar detta i fixering av den röda allelen.

Grundareffekten är ett specialfall av en befolkningsflaskhals, som uppstår när en liten grupp i en population splittras från den ursprungliga befolkningen och bildar en ny. Det slumpmässiga urvalet av alleler i den nybildade nya kolonin förväntas på ett grovt sätt förvränga den ursprungliga populationen i åtminstone vissa avseenden. Det är till och med möjligt att antalet alleler för vissa gener i den ursprungliga populationen är större än antalet genkopior hos grundarna, vilket gör fullständig representation omöjlig. När en nybildad koloni är liten kan dess grundare starkt påverka befolkningens genetiska sammansättning långt in i framtiden.

Ett väldokumenterat exempel finns i Amish- migrationen till Pennsylvania 1744. Två medlemmar av den nya kolonin delade den recessiva allelen för Ellis-Van Crevelds syndrom . Medlemmar av kolonin och deras ättlingar tenderar att vara religiösa isolater och förblir relativt isolerade. Som ett resultat av många generationers inavel är Ellis-Van Crevelds syndrom nu mycket vanligare bland amisherna än i den allmänna befolkningen.

Skillnaden i genfrekvenser mellan den ursprungliga populationen och kolonin kan också få de två grupperna att divergera avsevärt under loppet av många generationer. När skillnaden, eller det genetiska avståndet, ökar, kan de två separerade populationerna bli distinkta, både genetiskt och fenetiskt , även om inte bara genetisk drift utan också naturligt urval, genflöde och mutation bidrar till denna divergens. Denna potential för relativt snabba förändringar i kolonins genfrekvens ledde till att de flesta forskare betraktade grundareffekten (och i förlängningen den genetiska driften) som en betydande drivkraft i utvecklingen av nya arter . Sewall Wright var den första att fästa denna betydelse vid slumpmässig drift och små, nyligen isolerade populationer med sin skiftande balansteori om artbildning. Efter Wright Ernst Mayr många övertygande modeller för att visa att nedgången i genetisk variation och liten populationsstorlek efter grundareffekten var avgörande för att nya arter skulle utvecklas. Det finns dock mycket mindre stöd för denna uppfattning idag eftersom hypotesen har testats upprepade gånger genom experimentell forskning och resultaten har i bästa fall varit tvetydiga.

Historia

Ytterligare information: Modern syntes (1900-talet)

Den slumpmässiga slumpens roll i evolutionen beskrevs först av Arend L. Hagedoorn och AC Hagedoorn-Vorstheuvel La Brand 1921. De betonade att slumpmässig överlevnad spelar en nyckelroll i förlusten av variation från populationer. Fisher (1922) svarade på detta med den första, om än marginellt felaktiga, matematiska behandlingen av "Hagedoorn-effekten". Noterbart förväntade han sig att många naturliga populationer var för stora (ett N ~10 000) för att effekterna av drift skulle vara betydande och trodde att drift skulle ha en obetydlig effekt på evolutionsprocessen. Den korrigerade matematiska behandlingen och termen "genetisk drift" myntades senare av en grundare av befolkningsgenetik , Sewall Wright . Hans första användning av termen "drift" var 1929, även om han vid den tiden använde det i betydelsen av en riktad förändringsprocess, eller naturligt urval. Slumpmässig drift med hjälp av samplingsfel kom att kallas "Sewall-Wright-effekten", även om han aldrig var helt bekväm med att se sitt namn ges till den. Wright hänvisade till alla förändringar i allelfrekvens som antingen "stabil drift" (t.ex. urval) eller "slumpmässig drift" (t.ex. provtagningsfel). "Drift" kom att antas som en teknisk term i stokastisk mening uteslutande. Idag definieras det vanligtvis ännu snävare, i termer av urvalsfel, även om denna snäva definition inte är universell. Wright skrev att "begränsningen av "slumpmässig drift" eller till och med "drift" till endast en komponent, effekterna av olyckor vid provtagning, tenderar att leda till förvirring. Sewall Wright betraktade processen med slumpmässig genetisk drift med hjälp av provtagningsfel som var likvärdig med inavel, men senare arbete har visat att de är distinkta.

I början av den moderna evolutionära syntesen började forskare blanda den nya vetenskapen om populationsgenetik med Charles Darwins teori om naturligt urval. Inom denna ram fokuserade Wright på effekterna av inavel på små relativt isolerade populationer. Han introducerade konceptet med ett adaptivt landskap där fenomen som korsning och genetisk drift i små populationer kunde driva dem bort från adaptiva toppar, vilket i sin tur tillåter naturligt urval att driva dem mot nya adaptiva toppar. Wright trodde att mindre populationer var mer lämpade för naturligt urval eftersom "inavel var tillräckligt intensiv för att skapa nya interaktionssystem genom slumpmässig drift men inte tillräckligt intensiv för att orsaka slumpmässig icke-adaptiv fixering av gener".

Wrights åsikter om den genetiska driftens roll i det evolutionära systemet var kontroversiella nästan från första början. En av de mest högljudda och inflytelserika kritikerna var kollegan Ronald Fisher. Fisher medgav att genetisk drift spelade en viss roll i evolutionen, men en obetydlig sådan. Fisher har anklagats för att ha missförstått Wrights åsikter eftersom Fisher i sin kritik verkade hävda att Wright nästan helt hade avvisat urval. För Fisher var det enda sättet att förklara den ständigt ökande komplexiteten från enklare former att se evolutionsprocessen som en lång, stadig, adaptiv progression. Men debatterna har fortsatt mellan "gradualisterna" och de som lutar mer åt Wright-modellen för evolution där urval och drift tillsammans spelar en viktig roll.

1968 återuppväckte Motoo Kimura debatten med sin neutrala teori om molekylär evolution , som hävdar att de flesta av de genetiska förändringarna orsakas av genetisk drift som verkar på neutrala mutationer.

Rollen av genetisk drift med hjälp av provtagningsfel i evolutionen har kritiserats av John H. Gillespie och William B. Provine , som hävdar att urval på länkade platser är en viktigare stokastisk kraft.

Se även

• Peripatrisk artbildning
• Antigen drift
• Koalescent teori
• Konstruktiv neutral utveckling
• Genpool
• Meiotisk drift

Bibliografi

•     Avers CJ (1989). Process och mönster i evolutionen . New York: Oxford University Press . ISBN 0-19-505275-7 . LCCN 88005368 . OCLC 17677554 .
•     Barton NH , Briggs DE , Eisen JA , Goldstein DB , Patel NH (2007). Evolution . Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press . ISBN 978-0-87969-684-9 . LCCN 2007010767 . OCLC 86090399 .
•     Campbell NA (1996). Biologi . Benjamin/Cummings Series in the Life Sciences (4:e upplagan). Menlo Park, CA: Benjamin/Cummings Pub. Co. ISBN 0-8053-1940-9 . LCCN 95045572 . OCLC 33333455 .
•    Cavalli-Sforza LL , Menozzi P, Piazza A (1996). The History and Geography of Human Genes (Förkortad pocketutgåva). Princeton, NJ: Princeton University Press . ISBN 0-691-02905-9 . OCLC 35527063 .
•     Ewens WJ (2004). Matematisk populationsgenetik I. Teoretisk introduktion . Tvärvetenskaplig tillämpad matematik. Vol. 27 (andra upplagan). New York: Springer-Verlag . ISBN 0-387-20191-2 . LCCN 2003065728 . OCLC 53231891 .
•     Freeman S, Herron JC (2007). Evolutionär analys (4:e upplagan). Upper Saddle River, NJ: Pearson Prentice Hall . ISBN 978-0-13-227584-2 . LCCN 2006034384 . OCLC 73502978 .
•     Futuyma D (1998). Evolutionär biologi (3:e upplagan). Sunderland, MA: Sinauer Associates . ISBN 0-87893-189-9 . LCCN 97037947 . OCLC 37560100 .
•     Golding B, red. (1994). Icke-neutral evolution: teorier och molekylära data . New York: Chapman & Hall . ISBN 0-412-05391-8 . LCCN 93047006 . OCLC 29638235 . "Papper från en workshop sponsrad av Canadian Institute for Advanced Research ."
•     Hartl DL, Clark AG (2007). Principles of Population Genetics (4:e upplagan). Sunderland, MA: Sinauer Associates. ISBN 978-0-87893-308-2 . LCCN 2006036153 . OCLC 75087956 .
•     Hedrick PW (2005). Genetics of Populations (3:e upplagan). Boston, MA: Jones and Bartlett Publishers . ISBN 0-7637-4772-6 . LCCN 2004056666 . OCLC 56194719 .
•     Hej J , Fitch WM , Ayala FJ , red. (2005). Systematik och arternas uppkomst: På Ernst Mayrs 100-årsjubileum . Washington, DC: National Academies Press . ISBN 978-0-309-09536-5 . LCCN 2005017917 . OCLC 70745851 .
•     Howard DJ, Berlocher SH, red. (1998). Ändlösa former: arter och arter . New York: Oxford University Press. ISBN 978-0-19-510901-6 . LCCN 97031461 . OCLC 37545522 .
•      Kimura M , Ohta T (1971). Teoretiska aspekter av populationsgenetik . Monografier i befolkningsbiologi. Vol. 4. Princeton, NJ: Princeton University Press . s. 1–219. ISBN 0-691-08096-8 . LCCN 75155963 . OCLC 299867647 . PMID 5162676 .
•     Larson EJ (2004). Evolution: The Remarkable History of a Scientific Theory . Modern Library Chronicles. Vol. 17. New York: Modern Library . ISBN 0-679-64288-9 . LCCN 2003064888 . OCLC 53483597 .
•     Li W , Graur D (1991). Grunderna i molekylär evolution . Sunderland, MA: Sinauer Associates. ISBN 0-87893-452-9 . LCCN 90043581 . OCLC 22113526 .
•     Lynch M (2007). Ursprunget till genomarkitektur . Sunderland, MA: Sinauer Associates. ISBN 978-0-87893-484-3 . LCCN 2007000012 . OCLC 77574049 .
•     Miller G (2000). The Mating Mind: Hur sexuellt val formade utvecklingen av den mänskliga naturen . New York: Doubleday . ISBN 0-385-49516-1 . LCCN 00022673 . OCLC 43648482 .
•     Sadava D, Heller HC , Orians GH , Purves WK, Hillis DM (2008). Life: The Science of Biology . Vol. II: Evolution, mångfald och ekologi (8:e upplagan). Sunderland, MA; Gordonsville, VA: Sinauer Associates; WH Freeman och Company . ISBN 978-0-7167-7674-1 . LCCN 2006031320 . OCLC 71632224 .
•     Stevenson JC (1991). Ordbok över begrepp i fysisk antropologi . Referenskällor för samhällsvetenskap och humaniora. Vol. 10. Westport, CT: Greenwood Press . ISBN 0-313-24756-0 . LCCN 90022815 . OCLC 22732327 .
•      Tian JP (2008). Evolutionsalgebror och deras tillämpningar . Föreläsningsanteckningar i matematik. Vol. 1921. Berlin; New York: Springer. doi : 10.1007/978-3-540-74284-5 . ISBN 978-3-540-74283-8 . LCCN 2007933498 . OCLC 173807298 . Zbl 1136.17001 .
•     Wolf JB, Brodie ED, Wade MJ , red. (2000). Epistasis och evolutionsprocessen . Oxford, Storbritannien; New York: Oxford University Press. ISBN 0-19-512806-0 . LCCN 99046515 . OCLC 42603105 .
•     Zimmer C (2001). Evolution: The Triumph of an Idea . Inledning av Stephen Jay Gould ; förord ​​av Richard Hutton (1:a uppl.). New York: HarperCollins . ISBN 0-06-019906-7 . LCCN 2001024077 . OCLC 46359440 .

externa länkar

• Sheehy, Bob. "Simuleringsprogram för befolkningsgenetik" . Radford, VA: Radford University . Hämtad 21 december 2015 .
• Grimes, Bill. "Genetisk driftsimulering" . Tucson, Arizona: University of Arizona . Hämtad 25 augusti 2016 .