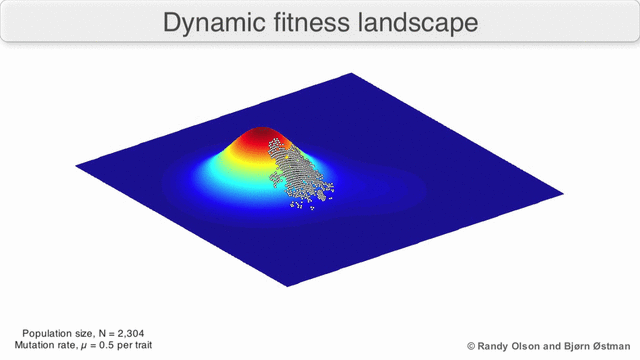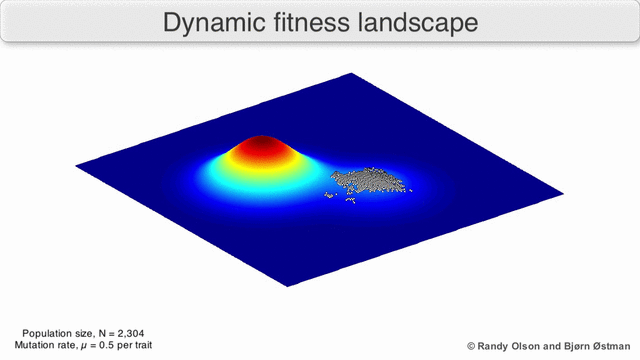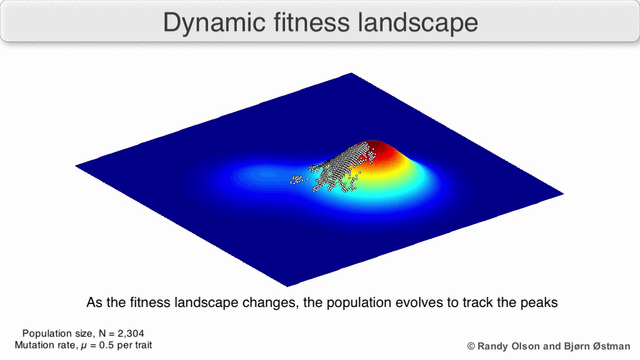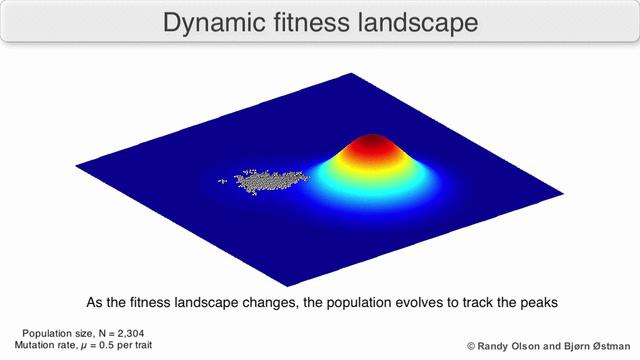
Fitness landskap

Inom evolutionär biologi används fitnesslandskap eller adaptiva landskap (typer av evolutionära landskap ) för att visualisera förhållandet mellan genotyper och reproduktiv framgång . Det antas att varje genotyp har en väldefinierad replikationshastighet (ofta kallad fitness ). Denna kondition är "höjden" av landskapet. Genotyper som liknar varandra sägs vara "nära" varandra, medan de som är väldigt olika är "långt" från varandra. Uppsättningen av alla möjliga genotyper, deras grad av likhet och deras relaterade fitnessvärden kallas då ett fitnesslandskap. Idén med ett fitnesslandskap är en metafor som hjälper till att förklara bristfälliga former i evolutionen genom naturligt urval , inklusive exploateringar och fel hos djur som deras reaktioner på övernaturliga stimuli .

Idén att studera evolution genom att visualisera fördelningen av fitnessvärden som ett slags landskap introducerades först av Sewall Wright 1932.

I evolutionära optimeringsproblem är fitnesslandskap utvärderingar av en fitnessfunktion för alla kandidatlösningar (se nedan).

I biologi

Skiss av ett fitnesslandskap. Pilarna indikerar det föredragna flödet av en population i landskapet, och punkterna A och C är lokala optima. Den röda bollen indikerar en population som har flyttat från ett mycket lågt konditionsvärde till toppen av en topp.

I alla fitnesslandskap representerar höjden och är en visuell metafor för fitness . Det finns tre distinkta sätt att karakterisera de andra dimensionerna, även om avståndet i varje fall representerar och är en metafor för graden av olikhet.

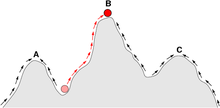
Fitnesslandskap uppfattas ofta som bergkedjor. Det finns lokala toppar (punkter varifrån alla stigar är nedförsbacke, dvs till lägre kondition) och dalar (regioner varifrån många stigar leder uppför). Ett fitnesslandskap med många lokala toppar omgivna av djupa dalar kallas robust. Om alla genotyper har samma replikationshastighet, å andra sidan, sägs ett fitnesslandskap vara platt. En växande befolkning klättrar vanligtvis uppför i fitnesslandskapet, genom en serie små genetiska förändringar, tills – inom den oändliga tidsgränsen – ett lokalt optimum uppnås.

Observera att ett lokalt optimum inte alltid kan hittas ens i evolutionär tid: om det lokala optimum kan hittas inom en rimlig tid kallas träningslandskapet "lätt" och om tiden som krävs är exponentiell kallas träningslandskapet " hård". Hårda landskap kännetecknas av den labyrintliknande egenskap genom vilken en allel som en gång var välgörande blir skadlig, vilket tvingar evolutionen att backa. Förekomsten av den labyrintliknande egenskapen i biofysiskt inspirerade fitnesslandskap kanske inte är tillräcklig för att skapa ett hårt landskap.

Visualisering av två dimensioner av ett NK fitnesslandskap . Pilarna representerar olika mutationsvägar som befolkningen kan följa medan de utvecklas i fitnesslandskapet.

Genotyp till fitnesslandskap

Wright visualiserade ett genotyprum som en hyperkub . Ingen kontinuerlig genotyp "dimension" definieras. Istället är ett nätverk av genotyper sammankopplade via mutationsvägar.

Stuart Kauffmans NK -modell faller inom denna kategori av fitnesslandskap. Nyare nätverksanalystekniker som SWAG (selektionsviktad attraktionsgraf) använder också ett dimensionslöst genotyputrymme.

Allelfrekvens till fitnesslandskap

Wrights matematiska arbete beskrev fitness som en funktion av allelfrekvenser. Här beskriver varje dimension en allelfrekvens vid en annan gen och går mellan 0 och 1.

Fenotyp till fitnesslandskap

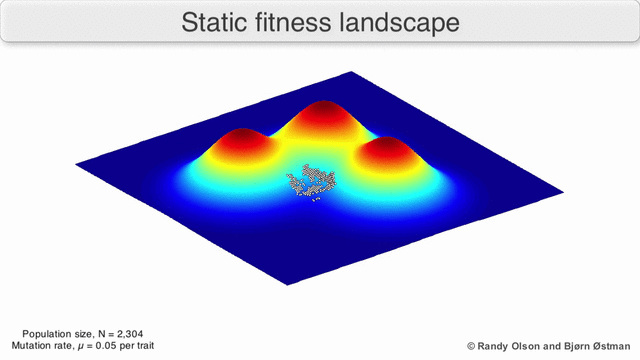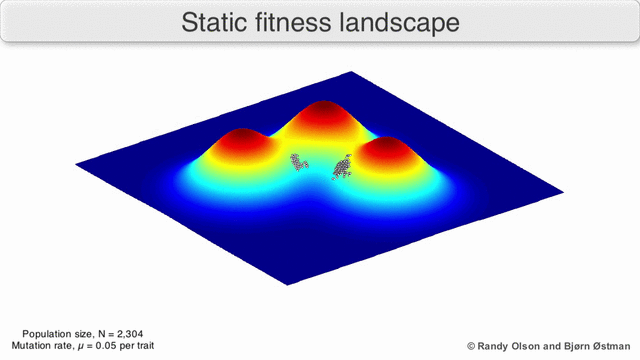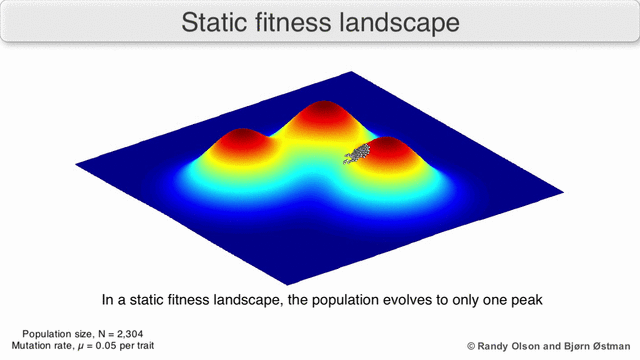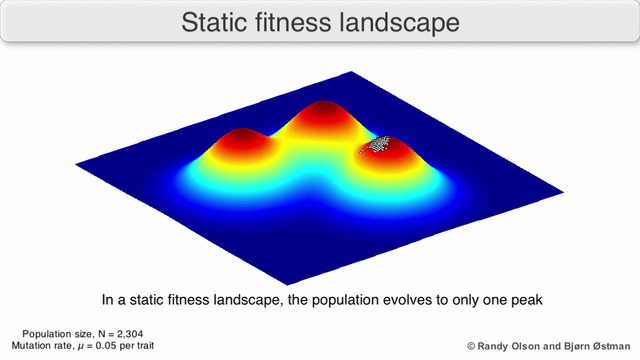
I den tredje typen av fitnesslandskap representerar varje dimension en annan fenotypisk egenskap. Under antaganden om kvantitativ genetik kan dessa fenotypiska dimensioner kartläggas på genotyper. Se visualiseringarna nedan för exempel på fenotyp till träningslandskap.

I evolutionär optimering

Förutom fältet evolutionär biologi har konceptet med ett fitnesslandskap också fått betydelse i evolutionära optimeringsmetoder som genetiska algoritmer eller evolutionsstrategier . I evolutionär optimering försöker man lösa verkliga problem (t.ex. ingenjörs- eller logistikproblem ) genom att imitera dynamiken i biologisk evolution. Till exempel kan en lastbil med ett antal destinationsadresser ta en mängd olika rutter, men endast ett fåtal kommer att resultera i kort körtid.

För att kunna använda många vanliga former av evolutionär optimering måste man definiera för alla möjliga lösningar på problemet av intresse (dvs. varje möjlig väg i fallet med lastbilen) hur "bra" den är. Detta görs genom att introducera en skalär -värderad funktion f(s) (skalär värderad betyder att f(s) är ett enkelt tal, såsom 0,3, medan s kan vara ett mer komplicerat objekt, till exempel en lista med destinationsadresser i fallet med lastbilen), som kallas fitnessfunktionen .

Ett högt f(s) innebär att s är en bra lösning. När det gäller lastbilen f(s) vara antalet leveranser per timme på rutt s . Den bästa, eller åtminstone en mycket bra, lösningen hittas sedan på följande sätt: initialt skapas en population av slumpmässiga lösningar. Sedan muteras lösningarna och väljs ut för dem med högre kondition, tills en tillfredsställande lösning har hittats.

Evolutionära optimeringstekniker är särskilt användbara i situationer där det är lätt att bestämma kvaliteten på en enskild lösning, men svårt att gå igenom alla möjliga lösningar en efter en (det är lätt att bestämma körtiden för en viss rutt för lastbilen , men det är nästan omöjligt att kontrollera alla möjliga rutter när antalet destinationer växer till mer än en handfull).

Även i de fall där en fitnessfunktion är svår att definiera kan konceptet med ett fitnesslandskap vara användbart. Till exempel, om konditionsutvärderingen sker genom stokastisk provtagning, är provtagningen från en (vanligtvis okänd) fördelning vid varje punkt; ändå kan det vara användbart att resonera om landskapet som bildas av den förväntade konditionen vid varje punkt. Om konditionen förändras med tiden (dynamisk optimering) eller med andra arter i miljön (samevolution) kan det ändå vara användbart att resonera kring banorna för det momentana fitnesslandskapet. Men i vissa fall (till exempel preferensbaserad interaktiv evolutionär beräkning) är relevansen mer begränsad, eftersom det inte finns någon garanti för att mänskliga preferenser överensstämmer med en enda träningsuppgift.

Konceptet med en skalärvärderad konditionsfunktion f(s) motsvarar också begreppet en potential- eller energifunktion inom fysiken . De två begreppen skiljer sig bara åt genom att fysiker traditionellt tänker i termer av att minimera den potentiella funktionen, medan biologer föredrar uppfattningen att konditionen maximeras. Om man tar inversen av en potentiell funktion förvandlas den därför till en fitnessfunktion och vice versa.

Varningar och begränsningar

Det finns flera viktiga varningar. Eftersom det mänskliga sinnet kämpar för att tänka i mer än tre dimensioner, kan 3D-topologier vilseleda när man diskuterar mycket multidimensionella fitnesslandskap. I synnerhet är det inte klart om toppar i naturliga biologiska fitnesslandskap någonsin verkligen separeras av fitnessdalar i sådana flerdimensionella landskap, eller om de är förbundna med enormt långa neutrala åsar. Dessutom är träningslandskapet inte statiskt i tiden utan beroende av den föränderliga miljön och utvecklingen av andra gener. Det är därför mer av ett havslandskap, vilket ytterligare påverkar hur åtskilda adaptiva toppar faktiskt kan vara. Dessutom är det relevant att ta hänsyn till att ett landskap i allmänhet inte är en absolut utan en relativ funktion. Slutligen, eftersom det är vanligt att använda funktion som en proxy för fitness när man diskuterar enzymer, existerar alla promiskuösa aktiviteter som överlappande landskap som tillsammans kommer att bestämma den ultimata lämpligheten för organismen, vilket innebär ett gap mellan olika samexisterande relativa landskap.

Med dessa begränsningar i åtanke kan fitnesslandskap fortfarande vara ett lärorikt sätt att tänka på evolution. Det är i grunden möjligt att mäta (även om det inte är för att visualisera) några av parametrarna för landskapets robusthet och toppantal, höjd, separation och klustring. Förenklade 3D-landskap kan sedan användas i förhållande till varandra för att visuellt representera relevanta funktioner. Dessutom kan fitnesslandskap av små undergrupper av evolutionära vägar konstrueras och visualiseras experimentellt, vilket potentiellt avslöjar funktioner som fitnesstoppar och dalar. Fitnesslandskap med evolutionära vägar indikerar de troliga evolutionära stegen och slutpunkterna bland uppsättningar av individuella mutationer.

Se även

• Viral kvasiart

externa länkar

Exempel på visualiserade fitnesslandskap

• Video: Använd träningslandskap för att visualisera evolution i aktion
• BEACON Blog—Evolution 101: Fitness Landscapes
• Pleiotropy Blog – en intressant diskussion om Sergey Gavrilets bidrag
• Pup Fish Evolution—UC Davis
• Evolution 101 – Shifting Balance Theory (Figur längst ner på sidan)
• Överlagra evolutionära banor på fitnesslandskap i virtuell verklighet

Vidare läsning

• Motbalans: Evolution som rörelse genom ett fitnesslandskap – en intressant (om bristfällig) diskussion om evolution och fitnesslandskap
• Exempel på användningen av evolutionära landskap i att tänka och tala om evolution
•   Hendrik Richter; Andries P. Engelbrecht (2014). Nya framsteg i teorin och tillämpningen av fitnesslandskap . ISBN 978-3-642-41888-4 .
•   Beerenwinkel, Niko; Pachter, Lior; Sturmfels, Bernd (2007). "Epistas och former av fitnesslandskap". Statistica Sinica . 17 (4): 1317–42. arXiv : q-bio.PE/0603034 . Bibcode : 2006q.bio.....3034B . MR 2398598 .
•   Richard Dawkins (1996). Att klättra på Mount Improbable . ISBN 0-393-03930-7 .
•   Sergey Gavrilets (2004). Fitnesslandskap och arternas ursprung . ISBN 978-0-691-11983-0 .
•   Stuart Kauffman (1995). Hemma i universum: sökandet efter lagar om självorganisering och komplexitet . ISBN 978-0-19-511130-9 .
•   Melanie Mitchell (1996). En introduktion till genetiska algoritmer (PDF) . ISBN 978-0-262-63185-3 .
•   Langdon, WB; Poli, R. (2002). "Kapitel 2 Fitnesslandskap" . Grunderna för genetisk programmering . ISBN 3-540-42451-2 .
•   Stuart Kauffman (1993). Ordningens ursprung . ISBN 978-0-19-507951-7 .
•    Poelwijk, Frank J; Kiviet, Daniel J; Weinreich, Daniel M; Tans, Sander J (2007). "Empiriska fitnesslandskap avslöjar tillgängliga evolutionära vägar". Naturen . 445 (7126): 383–6. Bibcode : 2007Natur.445..383P . doi : 10.1038/nature05451 . PMID 17251971 . S2CID 4415468 .