Faktoriell

Den här artikeln handlar om produkter av på varandra följande heltal. För statistiska experiment över alla kombinationer av värden, se faktorexperiment . För datarepresentation av oberoende komponenter, se faktorkod .

Utvalda fakulteter; värden i vetenskaplig notation är avrundade

$n$	$n!$
0	1
1	1
2	2
3	6
4	24
5	120
6	720
7	5 040
8	40 320
9	362 880
10	3 628 800
11	39 916 800
12	479 001 600
13	6 227 020 800
14	87 178 291 200
15	1 307 674 368 000
16	20 922 789 888 000
17	355 687 428 096 000
18	6 402 373 705 728 000
19	121 645 100 408 832 000
20	2 432 902 008 176 640 000
25	1 551 121 004 × 10 25
50	3,041 409 320 × 10 64
70	1,197 857 167 × 10 100
100	9,332 621 544 × 10 157
450	1 733 368 733 × 10 1 000
1 000	4,023 872 601 × 10 2 567
3 249	6,412 337 688 × 10 10 000
10 000	2,846 259 681 × 10 35 659
25 206	1,205 703 438 × 10 100 000
100 000	2,824 229 408 × 10 456 573
205 023	2,503 898 932 × 10 1 000 004
1 000 000	8,263 931 688 × 10 5 565 708
10 100	10 10 101,998 109 775 4820

I matematik , faktorialen för ett icke-negativt heltal $displaystyle n}$ , med $n!$ , betecknat ! är produkten av alla positiva heltal mindre än eller lika med $n$ . Faktorialen för $n$ är också lika med produkten av $n$ med nästa mindre faktorial:

$${\begin{aligned}n!&=n\ gånger (n-1)\ gånger (n-2)\ gånger (n-3)\ gånger \cdots \ gånger 3\ gånger 2\ gånger 1\\ &=n\ gånger (n-1)!\\\end{aligned}}$$

Till exempel,

$$5!=5\ gånger 4!=5\ gånger 4\ gånger 3\ gånger 2\ gånger 1=120.$$

Värdet på 0! är 1, enligt konventionen för en tom produkt .

Faktorer har upptäckts i flera forntida kulturer, särskilt i indisk matematik i Jainlitteraturens kanoniska verk och av judiska mystiker i den talmudiska boken Sefer Yetzirah . Den faktoriella operationen påträffas inom många områden av matematiken, särskilt inom kombinatorik , där dess mest grundläggande användning räknar de möjliga distinkta sekvenserna – permutationerna – av $n$ distinkta objekt: det finns $n!$ . I matematisk analys används faktorialer i potensserier för exponentialfunktionen och andra funktioner, och de har även tillämpningar inom algebra , talteori , sannolikhetsteori och datavetenskap .

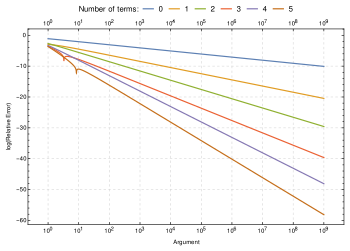
Mycket av matematiken för faktorialfunktionen utvecklades med början i slutet av 1700-talet och början av 1800-talet. Stirlings approximation ger en exakt approximation till factorialet av stora tal, vilket visar att det växer snabbare än exponentiell tillväxt . Legendres formel beskriver exponenterna för primtalen i en primtalsfaktorisering av faktorerna, och kan användas för att räkna de efterföljande nollorna för faktorerna. Daniel Bernoulli och Leonhard Euler interpolerade den faktoriella funktionen till en kontinuerlig funktion av komplexa tal , förutom vid de negativa heltal, (offset) gammafunktionen .

Många andra noterbara funktioner och nummersekvenser är nära släkt med faktorerna, inklusive de binomala koefficienterna , de dubbla faktorerna , de fallande faktorerna , de primära och subfaktorerna . Implementeringar av den faktoriella funktionen används ofta som exempel på olika datorprogrammeringsstilar och ingår i vetenskapliga miniräknare och bibliotek för vetenskapliga datorprogram. Även om direkt beräkning av stora faktoraler med hjälp av produktformeln eller upprepning inte är effektiv, är snabbare algoritmer kända, som inom en konstant faktor matchar tiden för snabba multiplikationsalgoritmer för tal med samma antal siffror.

Historia

Begreppet factorial har uppstått oberoende i många kulturer:

• I indisk matematik kommer en av de tidigaste kända beskrivningarna av factorials från Anuyogadvāra-sūtra, ett av Jainlitteraturens kanoniska verk, som har tilldelats datum varierande från 300 f.Kr. till 400 f.Kr. Den separerar den sorterade och omvända ordningen för en uppsättning artiklar från de andra ("blandade") beställningarna, och utvärderar antalet blandade beställningar genom att subtrahera två från den vanliga produktformeln för faktorn. Produktregeln för permutationer beskrevs också av Jain-munken Jinabhadra från 600-talet CE . Hinduforskare har använt faktorformler sedan åtminstone 1150, då Bhāskara II nämnde factorials i sitt verk Līlāvatī , i samband med ett problem om hur många sätt Vishnu kunde hålla sina fyra karakteristiska föremål (ett snäckaskal , diskus , muskotblomma och lotusblomma) . ) i sina fyra händer, och ett liknande problem för en gud med tio händer.
• I matematiken i Mellanöstern, listar den hebreiska mystiska skapelseboken Sefer Yetzirah , från den talmudiska perioden (200 till 500 e.Kr.), upp till 7 faktorer! som en del av en undersökning av antalet ord som kan bildas av det hebreiska alfabetet . Faktorer studerades också av liknande skäl av 700-talets arabiska grammatiker Al-Khalil ibn Ahmad al-Farahidi . Den arabiske matematikern Ibn al-Haytham (även känd som Alhazen, ca 965 – ca 1040) var den förste som formulerade Wilsons teorem som förband faktorialen med primtalen .
• I Europa, även om grekisk matematik inkluderade en del kombinatorik, och Platon berömt använde 5040 (en faktorial) som befolkningen i ett idealiskt samhälle, delvis på grund av dess delbarhetsegenskaper, finns det inga direkta bevis för antika grekiska studier av faktorialer. Istället var det första arbetet med factorials i Europa av judiska forskare som Shabbethai Donnolo , som förklarade Sefer Yetzirah-passagen. År 1677 beskrev den brittiske författaren Fabian Stedman tillämpningen av factorials för att ändra ringning , en musikalisk konst som involverar ringningen av flera stämda klockor.

Från slutet av 1400-talet och framåt blev factorials föremål för studier av västerländska matematiker. I en avhandling från 1494 beräknade den italienske matematikern Luca Pacioli factorials upp till 11!, i samband med ett problem med matbordsarrangemang. Christopher Clavius ​​diskuterade factorials i en kommentar från 1603 till Johannes de Sacroboscos arbete , och på 1640-talet publicerade den franske polymaten Marin Mersenne stora (men inte helt korrekta) tabeller med factorials, upp till 64!, baserade på Clavius ​​arbete. Potensserien för den exponentiella funktionen , med ömsesidiga faktorer för dess koefficienter, formulerades först 1676 av Isaac Newton i ett brev till Gottfried Wilhelm Leibniz . Andra viktiga verk av tidig europeisk matematik om faktorialer inkluderar omfattande täckning i en avhandling från 1685 av John Wallis , en studie av deras ungefärliga värden för stora värden på $n$ av Abraham de Moivre 1721, ett brev från James Stirling från 1729 till de Moivre anger vad som blev känt som Stirlings approximation , och arbete på samma gång av Daniel Bernoulli och Leonhard Euler som formulerar den kontinuerliga utvidgningen av den faktoriella funktionen till gammafunktionen . Adrien-Marie Legendre inkluderade Legendres formel , som beskrev exponenterna i faktoriseringen av faktoraler till primtal , i en text från 1808 om talteori .

Beteckningen $n!$ för factorials introducerades av den franske matematikern Christian Kramp 1808. Många andra notationer har också använts. En annan senare notation, där argumentet om faktorialet var halvt inneslutet av vänster och nedre sidor av en låda, var populär under en tid i Storbritannien och Amerika men föll ur bruk, kanske för att den är svår att typsätta. Ordet "faktoriell" (ursprungligen franska: factorielle ) användes första gången 1800 av Louis François Antoine Arbogast , i det första arbetet med Faà di Brunos formel, men med hänvisning till ett mer allmänt begrepp om produkter av aritmetiska progressioner . De "faktorer" som detta namn hänvisar till är termerna i produktformeln för faktorialen.

Definition

Faktorialfunktionen för ett positivt heltal $n$ definieras av produkten av alla positiva heltal som inte är större än $n$

$$n!=1\cdot 2\cdot 3\cdots (n-2)\cdot (n-1)\cdot n.$$

Detta kan skrivas mer kortfattat i produktnotation som

$$n!=\prod _{i=1}^{n}i.$$

Om denna produktformel ändras för att behålla alla utom den sista termen, skulle den definiera en produkt av samma form, för en mindre faktor. Detta leder till en återkommande relation , enligt vilken varje värde av faktorfunktionen kan erhållas genom att multiplicera det föregående värdet med $n$ :

$$n!=n\cdot (n-1)!.$$

Till exempel $5!=5\cdot 4!=5\cdot 24=120$ .

Faktoriell noll

Faktorialen för $0$ är ${\displaystyle 1} ,$ eller i symboler, $0!=1$ . Det finns flera motiv för denna definition:

• För $n=0$ , definitionen av $n!$ som en produkt involverar produkten av inga tal alls, och så är ett exempel på den bredare konventionen att den tomma produkten , en produkt av inga faktorer, är lika med den multiplikativa identiteten.
• Det finns exakt en permutation av noll objekt: med ingenting att permutera är den enda omarrangemangen att inte göra någonting.
• Denna konvention gör många identiteter i kombinatorik giltiga för alla giltiga val av deras parametrar. Till exempel är antalet sätt att välja alla $n$ element från en uppsättning av $n$${\textstyle {\tbinom {n}{n}}={\tfrac {n!}{n!0!}}=1,}$ en binomial koefficientidentitet som endast skulle vara giltig med $0!=1$ .
• Med $0!=1$ , återfallsrelationen för faktorialen förblir giltig vid $n=1$ . Därför, med denna konvention, behöver en rekursiv beräkning av faktorialen endast ha värdet för noll som basfall , vilket förenklar beräkningen och undviker behovet av ytterligare specialfall.
• Inställning $0!=1$ tillåter det kompakta uttrycket av många formler, såsom exponentialfunktionen , som en potensserie : ${\textstyle e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}.}$
• Detta val matchar gammafunktionen ${\displaystyle 0!=\Gamma (0+1)=1} ,$ och gammafunktionen måste ha detta värde för att vara en kontinuerlig funktion .

Ansökningar

De tidigaste användningarna av faktorfunktionen involverar att räkna permutationer : det finns $n!$ olika sätt att ordna $n$ distinkta objekt i en sekvens. Faktorer förekommer mer allmänt i många formler i kombinatorik , för att redogöra för olika ordningsföljder av objekt. Till exempel räknar binomialkoefficienterna ${\tbinom {n}{k}}$$k$ -elementkombinationerna (delmängder av $\displaystyle k}$ element) { från en mängd med $n$ element, och kan beräknas från fakulteter med hjälp av formeln

$${\binom {n}{k}}={\frac {n!}{k!(nk)!}}.$$

Stirlingtalen av det första slaget summerar till faktorerna och räknar permutationerna för $n$ grupperade i delmängder med samma antal cykler. En annan kombinatorisk tillämpning är att räkna avvikelser , permutationer som inte lämnar något element i sin ursprungliga position; antalet avvikelser av $n$ poster är det närmaste heltal till $n!/e$ .

I algebra uppstår faktorerna genom binomialsatsen , som använder binomialkoefficienter för att expandera summors styrkor. De förekommer också i de koefficienter som används för att relatera vissa familjer av polynom till varandra, till exempel i Newtons identiteter för symmetriska polynom . Deras användning vid räkning av permutationer kan också omarbetas algebraiskt: faktorerna är ordningarna för ändliga symmetriska grupper . I kalkyl förekommer faktorialer i Faà di Brunos formel för att kedja högre derivator. I matematisk analys förekommer faktorial ofta i nämnare av potensserier , framför allt i serierna för exponentialfunktionen ,

$$e^{x}=1+{\frac {x}{1}}+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6 }}+\cdots =\summa _{i=0}^{\infty }{\frac {x^{i}}{i!}},$$

och i koefficienterna för andra Taylor-serier (särskilt de för de trigonometriska och hyperboliska funktionerna ), där de upphäver faktorer för $n!$ kommer från $n$ :e derivatan av $x^{n}$ . Denna användning av faktorialer i potensserier kopplar tillbaka till analytisk kombinatorik genom den exponentiella genererande funktionen , som för en kombinatorisk klass med $n_{i}$ element av storlek $i$ definieras som potensserien

$$\sum _{i=0}^{\infty }{\frac {x^{i}n_{i}}{i!}}.$$

I talteorin är faktorernas mest framträdande egenskap delbarheten av $n!$ med alla positiva heltal upp till $n$ , mer exakt beskrivna för primtalsfaktorer med Legendres formel . Härav följer att godtyckligt stora primtal kan hittas som primtalsfaktorerna för talen $n!\pm 1$ , vilket leder till ett bevis för Euklids sats att antalet primtal är oändligt. När $n!\pm 1$ är i sig självt primtal kallas det ett faktoriellt primtal ; relaterat, Brocards problem , som också ställs av Srinivasa Ramanujan , gäller förekomsten av kvadrattal av formen $n!+1$ . Däremot siffrorna $n!+2,n!+3,\dots n!+n$ måste alla vara sammansatta, vilket bevisar förekomsten av godtyckligt stora primtalsluckor . Ett elementärt bevis för Bertrands postulat om förekomsten av ett primtal i valfritt intervall av formen ${\displaystyle [n,2n]} ,$ ett av de första resultaten av Paul Erdős , baserades på delbarhetsegenskaperna hos factorials. Faktorialtalssystemet är en blandad radixnotation för tal där platsvärdena för varje siffra är faktoriella .

Faktorer används flitigt i sannolikhetsteorin , till exempel i Poisson-fördelningen och i sannolikheterna för slumpmässiga permutationer . Inom datavetenskap , utöver att förekomma i analysen av brute-force-sökningar över permutationer, uppstår factorials i den nedre gränsen för $\log _{2}n!=n\log _{2}nO(n)$ på antalet jämförelser som behövs för att jämföra sortera en uppsättning av ${\ displaystyle n}$ objekt, och i analysen av kedjade hashtabeller , där fördelningen av nycklar per cell exakt kan approximeras med en Poisson-fördelning. Dessutom förekommer faktorialer naturligt i formler från kvantfysik och statistisk fysik , där man ofta överväger alla möjliga permutationer av en uppsättning partiklar. Inom statistisk mekanik måste beräkningar av entropi som Boltzmanns entropiformel eller Sackur-Tetrode-ekvationen korrigera antalet mikrotillstånd genom att dividera med fakulteterna av numren för varje typ av oskiljbar partikel för att undvika Gibbs-paradoxen . Kvantfysiken ger den underliggande anledningen till varför dessa korrigeringar är nödvändiga.

Egenskaper

Tillväxt och approximation

Jämförelse av faktorialen, Stirlings approximation och den enklare approximationen $(n/e)^{n}$ , på en dubbellogaritmisk skala

Relativt fel i en trunkerad Stirling-serie kontra antal termer

Huvudartikel: Stirlings approximation

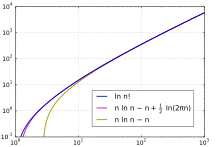
Som en funktion av $n$ växer har faktorialen snabbare än exponentiell tillväxt , men långsammare än en dubbel exponentiell funktion . Dess tillväxthastighet liknar n $\displaystyle n^{n}}$ , men långsammare med en exponentiell faktor. Ett sätt att närma sig detta resultat är att ta den naturliga logaritmen för faktorialen, som förvandlar dess produktformel till en summa, och sedan uppskatta summan med en integral:

$$\ln n!=\summa _{x=1}^{n}\ln x\approx \int _{1}^{n}\ln x\,dx=n\ln n-n+1.$$

Exponentiering av resultatet (och ignorerar den försumbara $+1$ termen) approximerar $n!$ som $(n/e)^{n}$ . Att mer noggrant begränsa summan både ovanför och under med en integral, med hjälp av trapetsregeln , visar att denna uppskattning behöver en korrektionsfaktor som är proportionell mot ${\sqrt {n}}$ . Proportionalitetskonstanten för denna korrigering kan hittas från Wallis-produkten , som uttrycker $\pi$ som ett begränsande förhållande mellan faktorial och två potenser. Resultatet av dessa korrigeringar är Stirlings approximation :

$$n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\,.$$

Här betyder $\sim$ -symbolen att när $n$ går till oändlighet, närmar sig förhållandet mellan vänster och höger sida ett i gränsen . Stirlings formel ger den första termen i en asymptotisk serie som blir ännu mer exakt när den tas till ett större antal termer:

$$n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\left(1+{\frac {1}{12n }}+{\frac {1}{288n^{2}}}-{\frac {139}{51840n^{3}}}-{\frac {571}{2488320n^{4}}}+\cdots \höger).$$

En alternativ version använder endast udda exponenter i korrigeringstermerna:

$$n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\exp \left({\frac {1}{12n }}-{\frac {1}{360n^{3}}}+{\frac {1}{1260n^{5}}}-{\frac {1}{1680n^{7}}}+\cdots \höger).$$

Många andra varianter av dessa formler har också utvecklats av Srinivasa Ramanujan , Bill Gosper och andra.

Den binära logaritmen för faktorialen, som används för att analysera jämförelsesortering , kan uppskattas mycket exakt med hjälp av Stirlings approximation. I formeln nedan anropar termen $O(1)$ stor O-notation .

$$\log _{2}n!=n\log _{2}n-(\log _{2}e)n+{\frac {1}{2}}\log _{2}n+O (1).$$

Delbarhet och siffror

Huvudartikel: Legendres formel

Produktformeln för faktorialet antyder att $n!$ är delbart med alla primtal som är högst n $\displaystyle n}$ , och med inga större primtal. Mer exakt information om dess delbarhet ges av Legendres formel , som ger exponenten för varje primtal $p$ i primtalsfaktoriseringen av $n!$ as

$$\sum _{i=1}^{\infty }\left\lfloor {\frac {n}{p^{i}}}\right\rfloor ={\frac {n-s_{p}( n)}{p-1}}.$$

Här betecknar $s_{p}(n)$ summan av basen - $p$ siffrorna i $n$ , och exponenten som ges av denna formel kan också tolkas i avancerad matematik som den p -adiska värderingen av faktorialet. Att tillämpa Legendres formel på produktformeln för binomialkoefficienter ger Kummers teorem , ett liknande resultat på exponenten för varje primtal i faktoriseringen av en binomialkoefficient. Att gruppera primtalsfaktorerna i faktorialet i primpotenser på olika sätt producerar multiplikativa partitioner av faktorialer .

Specialfallet med Legendres formel för $p=5$ ger antalet efterföljande nollor i decimalrepresentationen av faktorerna. Enligt denna formel kan antalet nollor erhållas genom att subtrahera basen-5 siffrorna i $n$ från $n$ , och dividera resultatet med fyra. Legendres formel innebär att exponenten för primtal $p=2$ alltid är större än exponenten för $p=5$ , så varje faktor av fem kan paras ihop med en faktor två att producera en av dessa avslutande nollor. De ledande siffrorna i faktorerna är fördelade enligt Benfords lag . Varje sekvens av siffror, i vilken bas som helst, är sekvensen av initiala siffror av något faktornummer i den basen.

$(n-1)!+1$ av faktorials, Wilsons sats , säger att är delbart med $n$ om och endast om $n$ är ett primtal . För ett givet heltal $x$ delar ges Kempner-funktionen för x {\displaystyle x} av den minsta n { \ $}$ n $vilken$ x $\displaystyle x}$$n!$ . För nästan alla tal (alla utom en delmängd av undantag med asymptotisk densitet noll) sammanfaller den med den största primfaktorn x $\displaystyle x}$ .

Produkten av två faktorer, $m!\cdot n!$ , delar alltid jämnt $(m+n)!$ . Det finns oändligt många faktorialer som är lika med produkten av andra faktorialer: om $n$ i sig är vilken produkt som helst av faktorialer, då $n!$ är lika med samma produkt multiplicerat med ytterligare en faktor, $(n-1)!$ . De enda kända exemplen på factorials som är produkter av andra factorials men inte är av denna "triviala" form är $9!=7!\cdot 3!\cdot 3!\cdot 2!$ , ${\displaystyle 10!=7!\cdot 6!=7!\cdot 5!\cdot 3!$ } och $16!=14!\cdot 5!\cdot 2!$ . Det skulle följa av abc- förmodan att det bara finns ändligt många icke-triviala exempel.

Den största gemensamma delaren av värdena för ett primitivt polynom av grad $d$ över heltal delar jämnt $d!$ .

Kontinuerlig interpolation och icke-heltalsgeneralisering

Gammafunktionen (skiftad en enhet kvar för att matcha faktorerna) interpolerar kontinuerligt de faktoriella värdena till icke-heltalsvärden

Absoluta värden för den komplexa gammafunktionen, som visar poler vid icke-positiva heltal

Huvudartikel: Gammafunktion

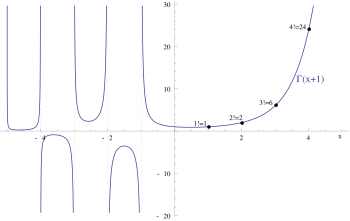
Det finns oändligt många sätt att utöka factorialerna till en kontinuerlig funktion . Den mest använda av dessa använder gammafunktionen , som kan definieras för positiva reella tal som integralen

$$\Gamma (z)=\int _{0}^{\infty }x^{z-1}e^{-x}\,dx.$$

Den resulterande funktionen är relaterad till faktorn för ett icke-negativt heltal $n$ med ekvationen

$$n!=\Gamma (n+1),$$

som kan användas som en definition av faktorn för icke-heltalsargument. Vid alla värden $x$ för vilka både $\Gamma (x)$ och $\Gamma (x-1)$ är definierade, följer gammafunktionen den funktionella ekvationen

$$\Gamma (n)=(n-1)\Gamma (n-1),$$

generalisering av återfallsrelationen för faktorialerna.

Samma integral konvergerar mer generellt för alla komplexa tal $z$ vars reella del är positiv. Det kan utökas till icke-heltalspunkterna i resten av det komplexa planet genom att lösa Eulers reflektionsformel

$$\Gamma (z)\Gamma (1-z)={\frac {\pi }{\sin \pi z}}.$$

Den här formeln kan dock inte användas vid heltal eftersom termen ${\displaystyle \sin \pi z} för dem$ skulle ge en division med noll . Resultatet av denna förlängningsprocess är en analytisk funktion , den analytiska fortsättningen av den integrerade formeln för gammafunktionen. Den har ett värde som inte är noll vid alla komplexa tal, förutom de icke-positiva heltal där den har enkla poler . På motsvarande sätt ger detta en definition för fakulteten vid alla komplexa tal förutom de negativa heltalen. En egenskap hos gammafunktionen, som skiljer den från andra kontinuerliga interpolationer av faktorialerna, ges av Bohr-Mollerups sats , som säger att gammafunktionen (offset med en) är den enda log-konvexa funktionen på de positiva reella talen som interpolerar faktorerna och följer samma funktionella ekvation. En relaterad unikhetssats av Helmut Wielandt säger att den komplexa gammafunktionen och dess skalära multipler är de enda holomorfa funktionerna på det positiva komplexa halvplanet som följer den funktionella ekvationen och förblir gränsade för komplexa tal med reell del mellan 1 och 2.

Andra komplexa funktioner som interpolerar faktorvärdena inkluderar Hadamards gammafunktion , som är en hel funktion över alla komplexa tal, inklusive de icke-positiva heltalen. I de p -adiska talen är det inte möjligt att kontinuerligt interpolera den faktoriella funktionen direkt, eftersom faktorerna för stora heltal (en tät delmängd av p -adicerna ) konvergerar till noll enligt Legendres formel, vilket tvingar fram en kontinuerlig funktion som är nära att deras värden ska vara noll överallt. Istället ger den p -adiska gammafunktionen en kontinuerlig interpolation av en modifierad form av faktorialet, och utelämnar de faktorer i faktorialet som är delbara med p .

Digammafunktionen är den logaritmiska derivatan av gammafunktionen . Precis som gammafunktionen ger en kontinuerlig interpolation av faktorerna, förskjuten med ett, ger digammafunktionen en kontinuerlig interpolation av övertonstalen, förskjuten av Euler-Mascheroni-konstanten .

Beräkning

TI SR-50A , en kalkylator från 1975 med en faktornyckel (tredje raden, mitten till höger)

Faktorialfunktionen är ett vanligt inslag i vetenskapliga miniräknare . Det ingår också i vetenskapliga programmeringsbibliotek som Python matematiska funktioner-modulen och Boost C++-biblioteket . Om effektivitet inte är ett problem, är beräkningsfaktorer trivialt: multiplicera bara successivt en variabel initierad till $1$ med heltal upp till $n$ . Enkelheten i denna beräkning gör den till ett vanligt exempel på användningen av olika datorprogrammeringsstilar och metoder.

Beräkningen av $n!$ kan uttryckas i pseudokod med iteration som

 definiera factorial(  n  ):  f  := 1 för  i  := 1, 2, 3, ...,  n  :  f  :=  f  ×  i  returnerar  f 

eller använda rekursion baserat på dess återkommande relation som

 definiera factorial(  n  ): om  n  = 0 returnera 1 return  n  × factorial(  n  − 1) 

Andra metoder som är lämpliga för dess beräkning inkluderar memoization , dynamisk programmering och funktionell programmering . Beräkningskomplexiteten hos dessa algoritmer kan analyseras med hjälp av enhetskostnadsmaskinmodellen med slumpmässig åtkomst , där varje aritmetisk operation tar konstant tid och varje nummer använder en konstant mängd lagringsutrymme. I denna modell kan dessa metoder beräkna $n!$ i tiden $O(n)$ , och den iterativa versionen använder mellanslag $O(1)$ . Om den inte är optimerad för svansrekursion tar den rekursiva versionen linjärt utrymme för att lagra sin anropsstack . Denna beräkningsmodell är dock endast lämplig när $n$ är tillräckligt liten för att tillåta $n!$ för att passa in i ett maskinord . Värdena 12! och 20! är de största faktorerna som kan lagras i 32-bitars respektive 64-bitars heltal . Flytande punkt kan representera större factorials, men ungefär snarare än exakt, och kommer fortfarande att svämma över för factorials större än $170!$ .

Den exakta beräkningen av större factorials involverar aritmetik med godtycklig precision, på grund av snabb tillväxt och heltalsspill . Beräkningstid kan analyseras som en funktion av antalet siffror eller bitar i resultatet. Enligt Stirlings formel, $n!$ har $b=O(n\log n)$ bitar. Schönhage –Strassen-algoritmen kan producera en $b$ -bit produkt i tid ${\displaystyle O(b\log b\log \log b)} ,$ och snabbare multiplikationsalgoritmer som tar tid $O(b\log b)$ är kända. Men att beräkna faktorialen involverar upprepade produkter snarare än en enkel multiplikation, så dessa tidsgränser gäller inte direkt. I den här inställningen beräknas $n!$ genom att multiplicera talen från 1 till $n$ i följd är ineffektivt, eftersom det involverar $n$ multiplikationer, varav en konstant bråkdel tar tid $O(n\log ^{2}n)$ vardera, vilket ger total tid $O(n^{2}\log ^{2}n)$ . Ett bättre tillvägagångssätt är att utföra multiplikationerna som en dividera-och-erövra-algoritm som multiplicerar en sekvens av $i$ -tal genom att dela upp den i två undersekvenser av $i/2$ -tal, multiplicerar varje undersekvens , och kombinerar resultaten med en sista multiplikation. Detta tillvägagångssätt till faktorialen tar total tid $O(n\log ^{3}n)$ : en logaritm kommer från antalet bitar i faktorialen, en andra kommer från multiplikationen algoritm, och en tredje kommer från dela och härska.

Ännu bättre effektivitet erhålls genom att beräkna n ! från dess primtalsfaktorisering, baserat på principen att exponentiering genom kvadrering är snabbare än att expandera en exponent till en produkt. En algoritm för detta av Arnold Schönhage börjar med att hitta listan med primtal upp till ${\displaystyle n} ,$ till exempel med hjälp av sikten av Eratosthenes , och använder Legendres formel för att beräkna exponenten för varje primtal. Sedan beräknar den produkten av primpotenserna med dessa exponenter, med hjälp av en rekursiv algoritm, enligt följande:

• Använd dividera och erövra för att beräkna produkten av primtal vars exponenter är udda
• Dela alla exponenterna med två (avrunda nedåt till ett heltal), beräkna rekursivt produkten av primpottserna med dessa mindre exponenter och kvadrera resultatet
• Multiplicera samman resultaten av de två föregående stegen

Produkten av alla primtal upp till $n$ är ett $O(n)$ -bittal, med primtalssatsen , så tiden för det första steget är $O(n\log ^{2}n)$ , där en logaritm kommer från dividera och erövra och en annan kommer från multiplikationsalgoritmen. I de rekursiva anropen till algoritmen kan primtalssatsen återigen anropas för att bevisa att antalet bitar i motsvarande produkter minskar med en konstant faktor på varje nivå av rekursion, så den totala tiden för dessa steg på alla nivåer av rekursion lägger till i en geometrisk serie till $O(n\log ^{2}n)$ . Tiden för kvadreringen i det andra steget och multiplikationen i det tredje steget är återigen ${\displaystyle O(n\log ^{2}n)} ,$ eftersom var och en är en enkel multiplikation av en nummer med $O(n\log n)$ bitar. Återigen, på varje nivå av rekursion har de inblandade talen en konstant bråkdel så många bitar (eftersom att upprepade gånger kvadrera dem skulle ge ett för stort slutresultat) så återigen adderas tidsmängderna för dessa steg i de rekursiva anropen i en geometrisk serie till $O(n\log ^{2}n)$ . Följaktligen tar hela algoritmen tid ${\displaystyle O(n\log ^{2}n)} ,$ proportionell mot en enkel multiplikation med samma antal bitar i resultatet.

Relaterade sekvenser och funktioner

Huvudartikel: Lista över faktoriella och binomiska ämnen

Flera andra heltalssekvenser liknar eller relaterade till faktorerna:

Alternerande faktorial

Den alternerande faktorialen är absolutvärdet av den alternerande summan av de första $n$ faktorerna, ${\textstyle \sum _{i=1}^{n}(-1)^{ni}i!}$ . Dessa har främst studerats i samband med deras primatitet; endast ändligt många av dem kan vara primtal, men en fullständig lista över primtal av denna form är inte känd.

Bhargava-faktorial

Bhargava -faktorialerna är en familj av heltalssekvenser definierade av Manjul Bhargava med liknande talteoretiska egenskaper som faktorialerna, inklusive själva faktorialen som ett specialfall.

Dubbelfaktorial

Produkten av alla udda heltal upp till något udda positivt heltal $n$ kallas dubbelfaktorialen av $n$ , och betecknas med $n!!$ . Det är,

$$(2k-1)!!=\prod _{i=1}^{k}(2i-1)={\frac {(2k)!}{2^{k}k!}}.$$

Till exempel 9!! = 1 × 3 × 5 × 7 × 9 = 945 . Dubbla faktorialer används i trigonometriska integraler , i uttryck för gammafunktionen vid halvheltal och volymerna av hypersfärer , och för att räkna binära träd och perfekta matchningar .

Exponentiell faktorial

Precis som triangulära tal summerar talen från $1$ till $n$ , och faktorialer tar sin produkt, exponentierar exponentialfaktorialen . Den exponentiella faktorialen definieras rekursivt som $a_{0}=1,\ a_{n}=n^{a_{n-1}}$ . Till exempel är den exponentiella faktorn 4

$$4^{3^{2^{1}}}=262144.$$

Dessa siffror växer mycket snabbare än vanliga factorials.

Fallande faktoral

Notationerna $(x)_{n}$ eller $x^{\underline {n}}$ används ibland för att representera produkten av $n$ heltal som räknas upp till och inklusive $x$ , lika med $x!/(xn)!$ . Detta är också känt som en fallande faktorial eller bakåtfaktor, och notationen $(x)_{n}$ är en Pochhammer-symbol. Fallande faktoraler räknar antalet olika sekvenser av $n$ distinkta objekt som kan dras från ett universum av $x$ objekt. De förekommer som koefficienter i de högre derivatorna av polynom och i faktormomenten för slumpvariabler .

Hyperfaktorer

Hyperfaktorerna för $n$ är produkten $displaystyle 1^{1}\cdot 2^{2}\cdots n^{n}}$ \ . Dessa siffror bildar diskriminanterna för hermitpolynom . De kan interpoleras kontinuerligt av K-funktionen och lyda analoger till Stirlings formel och Wilsons teorem.

Jordan–Pólya-siffror

Jordan –Pólya-talen är produkter av factorials, vilket tillåter upprepningar. Varje träd har en symmetrigrupp vars antal symmetrier är ett Jordan-Pólya-tal, och varje Jordan-Pólya-tal räknar symmetrierna för något träd.

Primorial

Primorial $n\#$ är produkten av primtal mindre än eller lika med ${\displaystyle n$ ; } denna konstruktion ger dem några liknande delbarhetsegenskaper som factorials, men till skillnad från factorials är de kvadratfria . Som med primtal $n!\pm 1$ , forskare har studerat primtal $n\#\pm 1$ .

Subfaktoriell

Underfaktor ger antalet avvikelser av en uppsättning av $displaystyle n}$ \ objekt. Det betecknas ibland $!n$ , och är lika med det heltal som ligger närmast $n!/e$ .

Superfaktoriell

Superfaktorial av $n$ är produkten av de första $\displaystyle n}$ { faktorerna. Superfaktorerna interpoleras kontinuerligt av Barnes G-funktionen .

externa länkar

• OEIS -sekvens A000142 (Faktornummer)
• "Faktoriell" . Encyclopedia of Mathematics . EMS Tryck på . 2001 [1994].
• Weisstein, Eric W. "Factorial" . MathWorld .