Funktion (matematik)

"f(x)" omdirigerar hit. Ej att förväxla med f(x) (musikgrupp) .

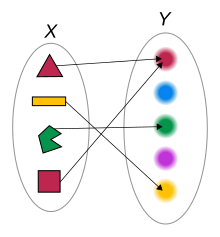
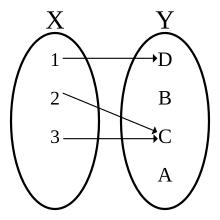
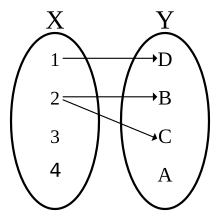
I matematik tilldelar en funktion från en mängd X till en mängd Y varje element i X exakt ett element av Y. Mängden X kallas funktionens domän och mängden Y kallas funktionens kodomän .

Funktioner var ursprungligen idealiseringen av hur en varierande kvantitet beror på en annan kvantitet. Till exempel är en planets position en funktion av tiden. Historiskt utvecklades konceptet med infinitesimalkalkylen i slutet av 1600-talet, och fram till 1800-talet var de funktioner som ansågs differentierbara (det vill säga de hade en hög grad av regelbundenhet). Begreppet funktion formaliserades i slutet av 1800-talet i termer av mängdlära , och detta utvidgade avsevärt tillämpningsområdena för konceptet.

En funktion betecknas oftast med bokstäver som f , g och h , och värdet av en funktion f vid ett element x i dess domän betecknas med f ( x ) ; det numeriska värdet som resulterar från funktionsutvärderingen vid ett speciellt ingångsvärde betecknas genom att ersätta x med detta värde; till exempel, värdet av f vid x = 4 betecknas med f (4) . När funktionen inte är namngiven och representeras av ett uttryck E , kan värdet på funktionen vid, säg, x = 4 betecknas med E | _{x =4} . Till exempel kan värdet vid 4 för funktionen som mappar x till $(x+1)^{2}$ betecknas med $\left.(x+1)^{2}\right\vert _{x=4}$ (vilket resulterar i 25).

En funktion representeras unikt av uppsättningen av alla par ( x , f ( x ) ) , kallad grafen för funktionen , ett populärt sätt att illustrera funktionen. När domänen och samdomänen är uppsättningar av reella tal, kan varje sådant par ses som de kartesiska koordinaterna för en punkt i planet.

Funktioner används i stor utsträckning inom naturvetenskap , teknik och inom de flesta områden av matematik. Det har sagts att funktioner är "de centrala undersökningsobjekten" inom de flesta matematikområden.

Schematisk skildring av en funktion beskriven metaforiskt som en "maskin" eller " svart låda " som för varje ingång ger en motsvarande utdata

Den röda kurvan är grafen för en funktion , eftersom varje vertikal linje har exakt en korsningspunkt med kurvan.

En funktion som associerar någon av de fyra färgade formerna till sin färg.

Definition

Diagram över en funktion, med domän X = {1, 2, 3} och kodomän Y = {A, B, C, D} , som definieras av uppsättningen ordnade par {(1, D), (2, C (3, C)} . Bilden/omfånget är uppsättningen {C, D} .

---

---

---

Detta diagram, som representerar uppsättningen av par {(1,D), (2,B), (2,C)} , definierar inte en funktion. En anledning är att 2 är det första elementet i mer än ett ordnat par, (2, B) och (2, C) , i denna uppsättning. Två andra skäl, som också är tillräckliga i sig, är att varken 3 eller 4 är första element (ingång) i något ordnat par däri.

En funktion från en mängd X till en mängd Y är en tilldelning av ett element av Y till varje element i X . Mängden X kallas funktionens domän och mängden Y kallas funktionens kodomän .

En funktion, dess domän och dess codomän deklareras av notationen f : X → Y , och värdet av en funktion f vid ett element x av X , betecknat med f(x) , kallas bilden av x under f , eller värdet av f tillämpat på argumentet x .

Funktioner kallas också kartor eller kartor , även om vissa författare gör viss skillnad mellan "kartor" och "funktioner" (se § Andra termer ).

Två funktioner f och g är lika om deras domän- och kodomänuppsättningar är samma och deras utvärden överensstämmer för hela domänen. Mer formellt, givet f : X → Y och g : X → Y , har vi f = g om och endast om f ( x ) = g ( x ) för alla x ∈ X .

Domänen och koddomänen ges inte alltid explicit när en funktion definieras, och utan någon (möjligen svår) beräkning kanske man bara vet att domänen ingår i en större uppsättning. Vanligtvis inträffar detta i matematisk analys , där "en funktion från X till Y " ofta hänvisar till en funktion som kan ha en riktig delmängd av X som domän. Till exempel kan en "funktion från realerna till realerna" hänvisa till en realvärderad funktion av en real variabel . En "funktion från de reella till de reella" betyder dock inte att funktionens domän är hela uppsättningen av de reella talen , utan bara att domänen är en uppsättning reella tal som innehåller ett icke-tomt öppet intervall . En sådan funktion kallas då en delfunktion . Till exempel, om f är en funktion som har de reella talen som domän och kodomän, då är en funktion som mappar värdet x till värdet g ( x ) = 1 / f ( x ) är en funktion g från realerna till realerna, vars domän är mängden av realerna x , så att f ( x ) ≠ 0 .

Omfånget eller bilden för en funktion är uppsättningen av bilder av alla element i domänen .

Totalt univalent förhållande

Vilken delmängd som helst av den kartesiska produkten av två mängder X och Y definierar en binär relation R ⊆ X × Y mellan dessa två mängder. Det är omedelbart att en godtycklig relation kan innehålla par som bryter mot de nödvändiga villkoren för en funktion som anges ovan.

En binär relation är univalent (även kallad högerunik) if

$\forall x\in X,\forall y\in Y,\forall z\in Y,\quad ((x,y)\in R\land (x,z)\in R)\implicerar y= z.$

En binär relation är total if

$\forall x\i X,\exists y\i Y,\quad (x,y)\i R.$

En partiell funktion är en binär relation som är univalent, och en funktion är en binär relation som är univalent och total.

Olika egenskaper hos funktioner och funktionssammansättning kan omformuleras i relationsspråket. Till exempel är en funktion injektiv om den omvända relationen R ^T ⊆ Y × X är univalent, där den omvända relationen definieras som R ^T = {( y , x ) | ( x , y ) ∈R } .

Ställ in exponentiering

Se även: Exponentiering § Anges som exponenter

Uppsättningen av alla funktioner från en uppsättning $X$ till en uppsättning $Y$ betecknas vanligtvis som

$Y^{X},$

som läses som $Y$ till potensen $X$ .

Denna notation är densamma som notationen för den kartesiska produkten av en familj av kopior av $Y$ indexerad med $X$ :

$Y^{X}=\prod _{x\in X}Y.$

Identiteten för dessa två beteckningar motiveras av det faktum att en funktion $f$ kan identifieras med elementet i den kartesiska produkten så att komponenten av index $x$ är $f(x)$ .

När $Y$ har två element, betecknas $Y^{X}}$ displaystyle vanligtvis $2^{X}$ och kallas potensmängden X . Den kan identifieras med uppsättningen av alla delmängder av $X$ , genom en-till-en-korrespondensen som associerar till varje delmängd $S\subseteq X$ funktionen $f$ så att $f(x)=1$ om $x\in S$ och $f(x)=0$ annars.

Notation

Det finns olika standardsätt för att beteckna funktioner. Den vanligaste notationen är funktionell notation, vilket är den första notationen som beskrivs nedan.

Funktionell notation

I funktionell notation får funktionen omedelbart ett namn, såsom f , och dess definition ges av vad f gör med det explicita argumentet x , med hjälp av en formel i termer av x . Till exempel betecknas funktionen som tar ett reellt tal som indata och matar ut det talet plus 1

$f(x)=x+1$ .

Om en funktion definieras i denna notation, tas dess domän och kodomän implicit att båda vara ${\displaystyle \mathbb {R} } ,$ uppsättningen av reella tal. Om formeln inte kan utvärderas med alla reella tal, så anses domänen implicit vara den maximala delmängden av $\mathbb {R}$ på vilken formeln kan utvärderas; se Domän för en funktion .

Ett mer komplicerat exempel är funktionen

$f(x)=\sin(x^{2}+1)$ .

det här exemplet tar funktionen f ett reellt tal som indata, kvadrerar det, adderar sedan 1 till resultatet, tar sedan sinus för resultatet och returnerar det slutliga resultatet som utdata.

När symbolen som betecknar funktionen består av flera tecken och ingen tvetydighet kan uppstå, kan parenteserna för funktionell notation utelämnas. Det är till exempel vanligt att skriva sin x istället för sin( x ) .

Funktionell notation användes först av Leonhard Euler 1734. Vissa ofta använda funktioner representeras av en symbol som består av flera bokstäver (vanligtvis två eller tre, vanligtvis en förkortning av deras namn). I det här fallet används vanligtvis en romersk typ istället, som " sin " för sinusfunktionen , i motsats till kursiv typsnitt för enbokstavssymboler.

När man använder denna notation stöter man ofta på missbruk av notation där notationen f ( x ) kan referera till värdet av f vid x , eller till själva funktionen. Om variabeln x deklarerades tidigare, betyder notationen f ( x ) entydigt värdet av f vid x . Annars är det användbart att förstå notationen som att den är båda samtidigt; detta gör att man kan beteckna sammansättning av två funktioner f och g på ett kortfattat sätt med beteckningen f ( g ( x )) .

Att särskilja f och f ( x ) kan dock bli viktigt i fall där funktioner i sig fungerar som indata för andra funktioner. (En funktion som tar en annan funktion som indata kallas en funktionell .) Andra metoder för att notera funktioner, som beskrivs nedan, undviker detta problem men är mindre vanliga.

Pilnotation

Pilnotation definierar regeln för en funktion inline, utan att ett namn måste ges till funktionen. Till exempel $x\mapsto x+1$ funktionen som tar ett reellt tal som indata och matar ut det numret plus 1. Återigen en domän och en koddomän av $\mathbb {R}$ antyds.

Domänen och koddomänen kan också uttryckligen anges, till exempel:

${\begin{aligned}\operatörsnamn {sqr} \colon \mathbb {Z} &\to \mathbb {Z} \\x&\mapsto x^{2}.\end{aligned}}$

Detta definierar en funktion sqr från heltal till heltal som returnerar kvadraten på dess indata.

Som en vanlig tillämpning av pilnotationen, anta ${\displaystyle f\colon X\times X\to Y;\;(x,t)\mapsto f(x,t)} är en$ funktion i två variabler, och vi vill referera till en delvis tillämpad funktion $X\to Y$ producerad genom att fixa det andra argumentet till värdet t ₀ utan att införa ett nytt funktionsnamn. Kartan i fråga skulle kunna betecknas $x\mapsto f(x,t_{0})$ med hjälp av pilnotationen. Uttrycket $x\mapsto f(x,t_{0})$ (läs: "kartan som tar x till en ₀ f ( x , t ) ") representerar denna nya funktion med bara argument, medan uttrycket ₀₀ f ( x , t ) hänvisar till värdet av funktionen f i punkten ₀₀ ( x , t ) .

Indexnotation

Indexnotation används ofta istället för funktionell notation. Det vill säga, istället för att skriva f ( x ) , skriver man $f_{x}.$

Detta är vanligtvis fallet för funktioner vars domän är uppsättningen av de naturliga talen . En sådan funktion kallas en sekvens , och i detta fall kallas elementet ${\displaystyle f_{n}} det$ n: te elementet i sekvensen.

Indexnotationen används också ofta för att skilja vissa variabler som kallas parametrar från de "sanna variablerna". Faktum är att parametrar är specifika variabler som anses vara fixerade under studiet av ett problem. Till exempel skulle kartan $x\mapsto f(x,t)$ (se ovan) betecknas $f_{t}$ med indexnotation, om vi definierar samlingen av kartor $f_{t}$ av formeln $f_{t}(x)=f(x,t)$ för alla $x,t\in X$ .

Punktnotation

I notationen $x\mapsto f(x),$ representerar inte symbolen x något värde, det är helt enkelt en platshållare som betyder att om x ersätts med något värde till vänster om pilen ska den ersättas med samma värde till höger om pilen. Därför x ersättas med vilken symbol som helst, ofta en interpunt " ⋅ ". Detta kan vara användbart för att särskilja funktionen f (⋅) från dess värde f ( x ) vid x .

Till exempel kan $a(\cdot )^{2}$ stå för funktionen $x\mapsto ax^{2}$ och ${\textstyle \int _{a}^{\,(\cdot )}f(u)\,du}$ kan stå för en funktion definierad av en integral med variabel övre gräns: ${\textstyle x\mapsto \int _{a}^{x}f(u)\,du}$ .

Specialiserade notationer

Det finns andra, specialiserade notationer för funktioner inom matematikens underdiscipliner. Till exempel, i linjär algebra och funktionell analys , betecknas linjära former och vektorerna de verkar på med hjälp av ett dubbelpar för att visa den underliggande dualiteten . Detta liknar användningen av bra–ket-notation i kvantmekanik. I logik och teorin om beräkning , funktion notation av lambda kalkyl används för att uttryckligen uttrycka de grundläggande begreppen funktionsabstraktion och tillämpning . I kategoriteori och homologisk algebra beskrivs nätverk av funktioner i termer av hur de och deras sammansättningar pendlar med varandra med hjälp av kommutativa diagram som utökar och generaliserar pilnotationen för funktioner som beskrivs ovan.

Andra villkor

För en bredare täckning av detta ämne, se Karta (matematik) .

Termin	Skillnad från "funktion"
Karta/Kartering	Ingen; termerna är synonyma.
	En karta kan ha vilken uppsättning som helst som sin koddomän, medan, i vissa sammanhang, typiskt i äldre böcker, koddomänen för en funktion specifikt är uppsättningen av reella eller komplexa tal.
	Alternativt är en karta associerad med en speciell struktur (t.ex. genom att explicit specificera en strukturerad koddomän i dess definition). Till exempel en linjär karta .
Homomorfism	En funktion mellan två strukturer av samma typ som bevarar strukturens funktioner (t.ex. en grupphomomorfism ) .
Morfism	En generalisering av homomorfismer till vilken kategori som helst , även när objekten i kategorin inte är mängder (till exempel definierar en grupp en kategori med endast ett objekt, som har gruppens element som morfismer; se Kategori (matematik) § Exempel för detta exempel och andra liknande).

En funktion kallas ofta också för en karta eller en kartläggning , men vissa författare gör skillnad på termen "karta" och "funktion". Till exempel är termen "karta" ofta reserverad för en "funktion" med någon sorts speciell struktur (t.ex. kartor över grenrör ) . Speciellt används karta ofta i stället för homomorfism för att vara kortfattad (t.ex. linjär karta eller karta från G till H istället för grupphomomorfism från G till H ). Vissa författare reserverar ordet mappning för det fall där koddomänens struktur uttryckligen tillhör definitionen av funktionen.

Vissa författare, som Serge Lang , använder "funktion" endast för att hänvisa till kartor där koddomänen är en delmängd av de reella eller komplexa talen, och använder termen avbildning för mer allmänna funktioner.

I teorin om dynamiska system betecknar en karta en evolutionsfunktion som används för att skapa diskreta dynamiska system . Se även Poincaré-karta .

Oavsett vilken definition av karta som används har relaterade termer som domän , codomain , injektiv , kontinuerlig samma betydelse som för en funktion.

Ange en funktion

Givet en funktion $f$ , per definition, till varje element $x$ i domänen för funktionen $f$ , finns det ett unikt element kopplat till det, värdet $f(x)$ av $f$ vid $x$ . Det finns flera sätt att specificera eller beskriva hur $x$ är relaterat till $f(x)$ , både explicit och implicit. Ibland hävdar ett teorem eller ett axiom existensen av en funktion som har vissa egenskaper, utan att beskriva den mer exakt. Ofta hänvisas till specifikationen eller beskrivningen som definitionen av funktionen $f$ .

Genom att lista funktionsvärden

På en finit uppsättning kan en funktion definieras genom att lista de element i koddomänen som är associerade med elementen i domänen. Till exempel, om $A=\{1,2,3\}$ så kan man definiera en funktion $f\colon A\to \ mathbb {R}$ med $f(1)=2,f(2)=3,f(3)=4.$

Med en formel

Funktioner definieras ofta av en formel som beskriver en kombination av aritmetiska operationer och tidigare definierade funktioner; En sådan formel gör det möjligt att beräkna värdet av funktionen från värdet av ett element i domänen. Till exempel, i exemplet ovan $f$ definieras med formeln $f(n)=n+1$ , för $n\in \{1,2,3\}$ .

När en funktion definieras på detta sätt är det ibland svårt att fastställa dess domän. Om formeln som definierar funktionen innehåller divisioner, måste värdena på variabeln för vilken en nämnare är noll exkluderas från domänen; sålunda, för en komplicerad funktion, går bestämningen av domänen genom beräkningen av nollorna för hjälpfunktioner. På liknande sätt, om kvadratrötter förekommer i definitionen av en funktion från $\mathbb {R}$ till $\mathbb {R} ,$ domänen ingår i uppsättningen av värden för variabeln för vilka argumenten för kvadratrötterna är icke-negativa.

Till exempel, $f(x)={\sqrt {1+x^{2}}}$ definierar en funktion $f\colon \mathbb {R} \to \mathbb {R}$ vars domän är $\mathbb {R} ,$ eftersom $1+x^{2}$ alltid är positivt om x är en reell siffra. Å andra sidan, $f(x)={\sqrt {1-x^{2}}}$ definierar en funktion från realerna till realerna vars domän reduceras till intervallet [−1, 1] . (I gamla texter kallades en sådan domän för definitionsdomänen för funktionen.)

Funktioner klassificeras ofta efter formlerna som definierar dem:

• En kvadratisk funktion är en funktion som kan skrivas $f(x)=ax^{2}+bx+c,$ där a , b , c är konstanter .
• Mer generellt är en polynomfunktion en funktion som kan definieras av en formel som endast involverar additioner, subtraktioner, multiplikationer och exponentiering till icke-negativa heltal. Till exempel, $f(x)=x^{3}-3x-1,$ och $f(x)=(x-1)(x^{3}+1)+2x^{2}-1.$
• En rationell funktion är densamma, med divisioner också tillåtna, såsom $f(x)={\frac {x-1}{x+1}},$ och $f(x)={\frac {1}{x+1}}+{\frac {3}{x}}-{\frac {2}{x-1}}.$
• En algebraisk funktion är densamma, med n :te rötter och rötter av polynom också tillåtna.
• En elementär funktion är densamma, med logaritmer och exponentialfunktioner tillåtna.

Inversa och implicita funktioner

En funktion $f\colon X\to Y,$ med domän X och kodomän Y , är bijektiv , om det för varje y i Y finns ett och bara ett element x i X så att y = f ( x ) . I det här fallet är den inversa funktionen av f funktionen $f^{-1}\colon Y\to X$ som mappar $y\in Y$ till elementet $x\in X$ så att y = f ( x ) . Till exempel är den naturliga logaritmen en bijektiv funktion från de positiva reella talen till de reella talen. Den har alltså en invers, kallad exponentialfunktionen , som mappar de reella talen på de positiva talen.

Om en funktion $f\colon X\to Y$ inte är bijektiv, kan det förekomma att man kan välja delmängder $E\subseteq X$ och $F \subseteq Y$ så att begränsningen av f till E är en bijektion från E till F , och har alltså en invers. De omvända trigonometriska funktionerna definieras på detta sätt. Till exempel cosinusfunktionen , genom begränsning, en bijektion från intervallet [0, π ] till intervallet [−1, 1] , och dess inversa funktion, kallad arccosine , mappar [−1, 1] till [0, π ] . De andra inversa trigonometriska funktionerna definieras på liknande sätt.

Mer generellt, givet en binär relation R mellan två uppsättningar X och Y , låt E vara en delmängd av X så att det för varje $x\in E,$ finns något $y \in Y$ så att x R y . Om man har ett kriterium som tillåter att välja ett sådant y för varje $x\in E,$ detta definierar en funktion $f\colon E\to Y,$ som kallas en implicit funktion , eftersom den är implicit definierad av relationen R .

Till exempel, ekvationen för enhetscirkeln x $\displaystyle x^{2}+y^{2}=1}$ definierar en relation på reella tal. Om −1 < x < 1 finns det två möjliga värden på y , ett positivt och ett negativt. För x = ± 1 blir dessa två värden båda lika med 0. Annars finns det inget möjligt värde på y . Detta betyder att ekvationen definierar två implicita funktioner med domän [−1, 1] och respektive kodomän [0, +∞) och (−∞, 0] .

I det här exemplet kan ekvationen lösas i y , vilket ger $y=\pm {\sqrt {1-x^{2}}},$ men i mer komplicerade exempel, detta är omöjligt. Till exempel, relationen $y^{5}+y+x=0$ definierar y som en implicit funktion av x , kallad Bring-radical , som har $\mathbb { R}$ som domän och intervall. Bring-radikalen kan inte uttryckas i termer av de fyra aritmetiska operationerna och n: e rötterna .

Den implicita funktionssatsen ger milda differentieringsvillkor för existens och unikhet hos en implicit funktion i närheten av en punkt.

Använder differentialkalkyl

Många funktioner kan definieras som antiderivatan av en annan funktion. Detta är fallet med den naturliga logaritmen , som är antiderivatan av 1/ x som är 0 för x = 1 . Ett annat vanligt exempel är felfunktionen .

Mer generellt kan många funktioner, inklusive de flesta specialfunktioner , definieras som lösningar av differentialekvationer . Det enklaste exemplet är förmodligen exponentialfunktionen , som kan definieras som den unika funktionen som är lika med sin derivata och tar värdet 1 för x = 0 .

Power-serier kan användas för att definiera funktioner på den domän där de konvergerar. Exponentialfunktionen ges till exempel av $e^{x}=\summa _{n=0}^{\infty }{x^{n} \över n!}$ . Men eftersom koefficienterna för en serie är ganska godtyckliga, definieras en funktion som är summan av en konvergent serie i allmänhet på annat sätt, och sekvensen av koefficienterna är resultatet av någon beräkning baserad på en annan definition. Därefter kan effektserien användas för att förstora funktionens domän. Vanligtvis, om en funktion för en reell variabel är summan av dess Taylor-serie i något intervall, tillåter denna potensserie att omedelbart förstora domänen till en delmängd av de komplexa talen , seriens konvergensskiva . Sedan analytisk fortsättning tillåter ytterligare förstoring av domänen för att inkludera nästan hela det komplexa planet . Denna process är den metod som vanligtvis används för att definiera logaritmen , exponential- och trigonometriska funktioner för ett komplext tal .

Genom återfall

Huvudartikel: Återkommande relation

Funktioner vars domän är de icke-negativa heltal, kända som sekvenser , definieras ofta av återkommande relationer .

Faktorialfunktionen på de icke-negativa heltalen ( $n\mapsto n!}$ displaystyle ) är ett grundläggande exempel, eftersom den kan definieras av återfallsrelationen

$n!=n(n-1)!\quad {\text{for}}\quad n>0,$

och initialtillståndet

$0!=1.$

Representerar en funktion

En graf används vanligtvis för att ge en intuitiv bild av en funktion. Som ett exempel på hur en graf hjälper till att förstå en funktion är det lätt att se från dess graf om en funktion ökar eller minskar. Vissa funktioner kan också representeras av stapeldiagram .

Grafer och plotter

Huvudartikel: Graf över en funktion

Funktionen kartlägger varje år dess dödstal i amerikanska motorfordon, visas som ett linjediagram

Samma funktion, visad som ett stapeldiagram

Givet en funktion ${\displaystyle f\colon X\to Y,} är$ dess graf formellt sett mängden

$G=\{(x,f(x))\mid x\in X\}.$

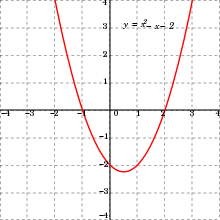
I det vanliga fallet där X och Y är delmängder av de reella talen (eller kan identifieras med sådana delmängder, t.ex. intervall ), kan ett element $(x,y)\in G$ vara identifieras med en punkt som har koordinaterna x , y i ett 2-dimensionellt koordinatsystem, t.ex. det kartesiska planet . Delar av detta kan skapa en tomt som representerar (delar av) funktionen. Användningen av plotter är så allmänt förekommande att de också kallas grafen för funktionen . Grafiska representationer av funktioner är också möjliga i andra koordinatsystem. Till exempel grafen för kvadratfunktionen

$x\mapsto x^{2},$

bestående av alla punkter med koordinater $(x,x^{2})$ för $x\in \mathbb {R} ,$ ger, när de avbildas i kartesiska koordinater , den välkända parabeln . Om samma kvadratiska funktion $x\mapsto x^{2},$ med samma formella graf, bestående av talpar, plottas istället i polära koordinater $(r,\theta )=(x,x^{2}),$ plotten som erhålls är Fermats spiral .

Tabeller

Huvudartikel: Matematisk tabell

En funktion kan representeras som en värdetabell. Om domänen för en funktion är finit, kan funktionen specificeras helt på detta sätt. Till exempel, multiplikationsfunktionen $f\colon \{1,\ldots ,5\}^{2}\to \mathbb {R}$ definierad som $f(x,y)=xy$ kan representeras av den välbekanta multiplikationstabellen

y x	1	2	3	4	5
1	1	2	3	4	5
2	2	4	6	8	10
3	3	6	9	12	15
4	4	8	12	16	20
5	5	10	15	20	25

Å andra sidan, om en funktions domän är kontinuerlig, kan en tabell ge funktionens värden vid specifika värden för domänen. Om ett mellanvärde behövs interpolation användas för att uppskatta värdet på funktionen. Till exempel kan en del av en tabell för sinusfunktionen ges enligt följande, med värden avrundade till 6 decimaler:

x	synd x
1,289	0,960557
1,290	0,960835
1,291	0,961112
1,292	0,961387
1,293	0,961662

Före tillkomsten av handhållna miniräknare och persondatorer sammanställdes och publicerades sådana tabeller ofta för funktioner som logaritmer och trigonometriska funktioner.

Stapeldiagram

Huvudartikel: Stapeldiagram

Stapeldiagram används ofta för att representera funktioner vars domän är en ändlig mängd, de naturliga talen eller heltal . I detta fall representeras ett element x i domänen av ett intervall av x -axeln, och motsvarande värde för funktionen, f ( x ) , representeras av en rektangel vars bas är intervallet som motsvarar x och vars höjd är f ( x ) (eventuellt negativt, i vilket fall staven sträcker sig under x -axeln).

Generella egenskaper

Detta avsnitt beskriver allmänna egenskaper hos funktioner, som är oberoende av specifika egenskaper hos domänen och koddomänen.

Standardfunktioner

Det finns ett antal standardfunktioner som förekommer ofta:

• För varje uppsättning X finns det en unik funktion, som kallas den tomma funktionen , eller tom karta , från den tomma uppsättningen till X . Grafen för en tom funktion är den tomma uppsättningen. Förekomsten av tomma funktioner behövs både för teorins koherens och för att undvika undantag som rör den tomma mängden i många påståenden. Under den vanliga mängdteoretiska definitionen av en funktion som en ordnad triplett (eller motsvarande), finns det exakt en tom funktion för varje mängd, alltså den tomma funktionen $\varnothing \mapsto X$ är inte lika med $\varnothing \mapsto Y$ om och endast om $X\neq Y$ , även om deras graf båda är den tomma mängden .
• För varje uppsättning X och varje singeluppsättning { s } finns det en unik funktion från X till { s } , som mappar varje element i X till s . Detta är en injektion (se nedan) om inte X är den tomma uppsättningen.
• Givet en funktion $f\colon X\to Y,$ den kanoniska avbildningen av f på dess bild $f(X )=\{f(x)\mid x\in X\}$ är funktionen från X till f ( X ) som mappar x till f ( x ) .
• För varje delmängd A av en mängd X är inkluderingskartan av A till X den injektiva (se nedan) funktion som mappar varje element i A till sig själv .
• Identitetsfunktionen på en mängd X , ofta betecknad med id _X , är inkluderingen av X i sig själv.

Funktionssammansättning

Huvudartikel: Funktionssammansättning

Givet två funktioner $f\colon X\to Y$ och $g\colon Y\to Z$ så att domänen för g är codomänen för f , deras sammansättning är funktionen $g\circ f\kolon X\högerpil Z$ definierad av

$(g\circ f)(x)=g(f(x)).$

Det vill säga, värdet av $g\circ f$ erhålls genom att först applicera f till x för att få y = f ( x ) och sedan tillämpa g på resultatet y för att få g ( y ) = g ( f ( x )) . I notationen skrivs alltid den funktion som tillämpas först till höger.

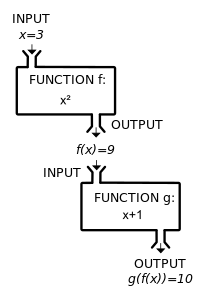
Sammansättningen $g\circ f$ är en operation på funktioner som endast definieras om koddomänen för den första funktionen är domänen för den andra. Även när både $g\circ f$ och $f\circ g$ uppfyller dessa villkor, är kompositionen inte nödvändigtvis kommutativ , det vill säga funktionerna $g\ circ f$ och $f\circ g$ behöver inte vara lika, men kan ge olika värden för samma argument. Låt till exempel f ( x ) = x ² och g ( x ) = x + 1 , sedan $g(f(x))=x^{2} +1$ och $f(g(x))=(x+1)^{2}$ håller med bara för $x=0.$

Funktionssammansättningen är associativ i den meningen att, om en av $(h\circ g)\circ f$ och $h\circ (g\ circ f)$ definieras, sedan definieras den andra också, och de är lika. Sålunda skriver man

$h\circ g\circ f=(h\circ g)\circ f=h\circ (g\circ f).$

Identitetsfunktionerna $\operatorname {id} _{X}}$ displaystyle och $\operatorname {id} _{Y}$ är en högeridentitet respektive en vänsteridentitet för funktioner från X till Y . Det vill säga, om f är en funktion med domän X , och kodomän Y , har man $f\circ \operatörsnamn {id} _{X}=\operatörsnamn {id} _{Y}\circ f=f.$

• 

  En sammansatt funktion g ( f ( x )) kan visualiseras som en kombination av två "maskiner".

• 

  Ett enkelt exempel på en funktionssammansättning

• 

  En annan komposition. I det här exemplet, ( g ∘ f )(c) = # .

Bild och förbild

Huvudartikel: Bild (matematik)

Låt $X\to Y.}$ colon Bilden under f av ett element x i domänen X är f ( x ) . Om A är någon delmängd av X , så är bilden av A under f , betecknad f ( A ) , delmängden av koddomänen Y som består av alla bilder av element i A , dvs.

$f(A)=\{f(x)\mid x\in A\}.$

Bilden av f är bilden av hela domänen, det vill säga f ( X ) . Det kallas också intervallet f , även om termen intervall också kan syfta på kodomänen .

Å andra sidan är den omvända bilden eller förbilden under f av ett element y i samdomänen Y uppsättningen av alla element i domänen X vars bilder under f är lika med y . I symboler betecknas förbilden av y med $f^{-1}(y)$ och ges av ekvationen

$f^{-1}(y)=\{x\in X\mid f(x)=y\}.$

På samma sätt är förbilden av en delmängd B av samdomänen Y uppsättningen av förbilderna av elementen i B , det vill säga den är delmängden av domänen X som består av alla element av X vars bilder tillhör B. Den betecknas med $f^{-1}(B)$ och ges av ekvationen

$f^{-1}(B)=\{x\in X\mid f(x)\in B\}.$

Till exempel är förbilden av $\{4,9\}$ under fyrkantsfunktionen mängden $\{-3,-2 ,2,3\}$ .

Per definition av en funktion är bilden av ett element x i domänen alltid ett enda element i kodomänen. Däremot kan förbilden $f^{-1}(y)$ för ett element y i koddomänen vara tom eller innehålla valfritt antal element. Till exempel, om f är funktionen från heltal till sig själva som mappar varje heltal till 0, då $f^{-1}(0)=\mathbb {Z}$ .

Om $f\colon X\to Y$ är en funktion, A och B är delmängder av X och C och D är delmängder av Y , då har en följande egenskaper:

• $A\subseteq B\Longrightarrow f(A)\subseteq f(B)$
• $C\subseteq D\Longrightarrow f^{-1}(C)\subseteq f^{-1}(D)$
• $A\subseteq f^{-1}(f(A))$
• $C\supseteq f(f^{-1}(C))$
• $f(f^{-1}(f(A)))=f(A)$
• $f^{-1}(f(f^{-1}(C)))=f^{-1 }(C)$

Förbilden av f av ett element y i kodomänen kallas ibland, i vissa sammanhang, fibern av y under f .

Om en funktion f har en invers (se nedan) betecknas denna invers $f^{-1}.$ I det här fallet kan $f^{-1}(C)$ beteckna antingen bilden med $f^{-1 }$ eller förbilden av f av C . Detta är inget problem, eftersom dessa uppsättningar är lika. Notationen $f(A)$ och $f^{-1}(C)$ kan vara tvetydig i fallet med mängder som innehåller vissa delmängder som element, såsom $\{x,\{x\}\}.$ I det här fallet kan viss försiktighet behövas, till exempel genom att använda hakparenteser $f[A ],f^{-1}[C]$ för bilder och förbilder av delmängder och vanliga parenteser för bilder och förbilder av element.

Injektiva, surjektiva och bijektiva funktioner

Låt $f\colon X\to Y$ vara en funktion.

Funktionen f är injektiv (eller en - till-en , eller är en injektion ) om f ( a ) ≠ f ( b ) för två olika element a och b i X. På motsvarande sätt är f injektiv om och endast om, för någon $y\in Y,$ förbilden $f^{-1}(y)$ innehåller högst ett element. En tom funktion är alltid injektiv. Om X inte är den tomma mängden, är f injektiv om och endast om det finns en funktion $g\colon Y\to X$ så att $g\ circ f=\operatörsnamn {id} _{X},$ det vill säga om f har en vänsterinvers . Bevis : Om f är injektiv, för att definiera g väljer man ett element $x_{0}$ i X (som existerar eftersom X antas vara icke-tomt), och man definierar g med $g( y)=x$ om $y=f(x)$ och $g(y)=x_{0}$ om $y\not \in f(X).$ Omvänt, om $g\circ f=\operatörsnamn {id} _{X},$ och $y=f(x),$ sedan $x=g(y),$ och därmed $f^{-1}(y)=\{x\}.$

Funktionen f är surjektiv (eller på , eller är en surjektion ) om dess område $f(X)$ är lika med dess koddomän ${\displaystyle Y} ,$ det vill säga om, för varje element ${\ displaystyle y}$ för codomänen, det finns något element $x$ i domänen så att $f(x)=y$ (med andra ord, förbilden $f^{-1}(y)$ av varje $y\in Y$ är inte tom). Om, som vanligt i modern matematik, valets axiom antas , så är f surjektiv om och endast om det finns en funktion $g\colon Y\to X$ så att $f\circ g=\operatörsnamn {id} _{Y},$ det vill säga om f har en höger invers . Valets axiom behövs, eftersom, om f är surjektiv, definierar man g med $g(y)=x,$ där $x$ är ett godtyckligt valt element i $f^{-1}(y).$

Funktionen f är bijektiv (eller är en bijektion eller en-till-en-korrespondens ) om den är både injektiv och surjektiv. Det vill säga, f är bijektiv om, för någon $y\in Y,$ förbilden $f^{-1}(y)$ innehåller exakt ett element. Funktionen f är bijektiv om och endast om den tillåter en invers funktion , det vill säga en funktion $g\colon Y\to X$ så att $g\circ f=\operatörsnamn {id} _{X}$ och $f\circ g=\operatörsnamn {id} _{Y}.$ (Till skillnad från fallet med surjektioner kräver detta inte valets axiom, beviset är enkelt).

Varje funktion $f\colon X\to Y$ kan faktoriseras som sammansättningen $i\circ s$ av en injektion följt av en injektion, där s är den kanoniska injektionen av X på f ( X ) och i är den kanoniska injektionen av f ( X ) i Y . Det här är kanonisk faktorisering av f .

"En-till-en" och "på" är termer som var vanligare i den äldre engelskspråkiga litteraturen; "injektiv", "surjektiv" och "bijektiv" myntades ursprungligen som franska ord under andra kvartalet av 1900-talet av Bourbaki- gruppen och importerades till engelska. är "en en-till-en-funktion" en som är injektiv, medan en "en-till-en-överensstämmelse" hänvisar till en bijektiv funktion. Även påståendet " f mappar X till Y " skiljer sig från " f mappar X till B ", genom att det förra antyder att f är surjektivt, medan det senare inte gör något påstående om f :s natur. I ett komplicerat resonemang kan skillnaden med en bokstav lätt missas. Förvirrande karaktär av denna äldre terminologi, har dessa termer minskat i popularitet i förhållande till de Bourbakiska termerna, som också har fördelen av att vara mer symmetriska.

Begränsning och förlängning

Huvudartikel: Restriktion (matematik)

Om $f\colon X\to Y$ är en funktion och S är en delmängd av X , då begränsningen av $f$ till S , betecknad $f|_{S}$ , är funktionen från S till Y definierad av

$f|_{S}(x)=f(x)$

för alla x i S . Restriktioner kan användas för att definiera partiella inversa funktioner : om det finns en delmängd S av domänen för en funktion $f$ så att $f|_{S}$ är injektiv, då den kanoniska antagandet av $f|_{S}$ på sin bild $f|_{S}(S)=f(S)$ är en bijektion och har alltså en invers funktion från $f(S)$ till S . En tillämpning är definitionen av inversa trigonometriska funktioner . Till exempel cosinusfunktionen injektiv när den är begränsad till intervallet [0, π ] . Bilden av denna begränsning är intervallet [−1, 1] , och därför har begränsningen en invers funktion från [−1, 1] till [0, π ] , som kallas arccosine och betecknas arccos .

Funktionsbegränsning kan också användas för att "limma ihop" funktioner. Låt ${\textstil X=\bigcup _{i\in I}U_{i}}$ vara nedbrytningen av X som en förening av delmängder, och antag att en funktion $f_{i}\colon U_{i}\to Y$ definieras på varje $U_{i}$ så att för varje par $i,j$ av index, begränsningarna för $f_{i}$ och $f_{j}$ till $U_{i}\cap U_ {j}$ är lika. Då definierar detta en unik funktion $f\kolon X\to Y$ så att $f|_{U_{i}}=f_{i}$ för alla i . Det är så här funktioner på grenrör definieras.

En förlängning av en funktion f är en funktion g så att f är en begränsning av g . En typisk användning av detta koncept är processen för analytisk fortsättning , som tillåter att utöka funktioner vars domän är en liten del av det komplexa planet till funktioner vars domän är nästan hela det komplexa planet.

Här är ett annat klassiskt exempel på en funktionsförlängning som man stöter på när man studerar homografier av den verkliga linjen . En homografi är en funktion $h(x)={\frac {ax+b}{cx+d}}$ så att ad − bc ≠ 0 . Dess domän är mängden av alla reella tal som skiljer sig från $-d/c,$ och dess bild är mängden av alla reella tal som skiljer sig från $a/c.$ Om man förlänger den reella linjen till den projektivt förlängda reella linjen ${\ displaystyle h(\infty )=a/c}$ att inkludera ∞ , kan man utöka h till en bijektion från den förlängda reella linjen till sig själv genom att sätta och $h(-d/c)=\infty$ .

Multivariat funktion

Ytterligare information: Verklig multivariatfunktion

Ej att förväxla med Multivalued-funktionen .

En binär operation är ett typiskt exempel på en bivariat funktion som tilldelar varje par $(x,y)$ resultatet $x\circ y$ .

En multivariatfunktion , eller funktion av flera variabler, är en funktion som beror på flera argument. Sådana funktioner förekommer ofta. Till exempel är en bils position på en väg en funktion av den tillryggalagda tiden och dess medelhastighet.

Mer formellt är en funktion av n variabler en funktion vars domän är en uppsättning av n -tupler. Till exempel är multiplikation av heltal en funktion av två variabler, eller bivariat funktion , vars domän är uppsättningen av alla par (2-tuplar) av heltal, och vars koddomän är uppsättningen av heltal. Detsamma gäller för varje binär operation . Mer generellt definieras varje matematisk operation som en multivariat funktion.

Den kartesiska produkten $X_{1}\times \cdots \times X_{n}$ av n set $X_{1},\ldots ,X_ {n}$ är mängden av alla n -tupler $(x_{1},\ldots ,x_{n})$ så att $x_{i}\in X_{i}$ för varje i med $1\leq i\leq n$ . Därför är en funktion av n variabler en funktion

$f\colon U\to Y,$

där domänen U har formen

$U\subseteq X_{1}\times \cdots \times X_{n}.$

När man använder funktionsnotation utelämnar man vanligtvis parentesen kring tupler, och skriver $f(x_{1},x_{2})$ istället för $f((x_{1},x_{2})).$

I det fall där alla $X_{i}$ är lika med mängden $\mathbb {R}$ av reella tal , har man en funktion av flera reella variabler . Om $X_{i}$ är lika med mängden $\mathbb {C}$ av komplexa tal , har man en funktion av flera komplexa variabler .

Det är vanligt att även beakta funktioner vars koddomän är en produkt av uppsättningar. Till exempel euklidisk division varje par ( a , b ) av heltal med b ≠ 0 till ett par heltal som kallas kvoten och resten :

${\begin{aligned}{\text{Euklidisk division}}\colon \quad \mathbb {Z} \times (\mathbb {Z} \setminus \{0\})&\to \mathbb {Z} \times \mathbb {Z} \\(a,b)&\mapsto (\operatörsnamn {kvot} (a,b),\operatörsnamn {rest} (a,b)).\end{aligned}}$

Kodomänen kan också vara ett vektorrum . I det här fallet talar man om en vektorvärderad funktion . Om domänen finns i ett euklidiskt utrymme , eller mer allmänt ett mångfaldigt , kallas en vektorvärderad funktion ofta ett vektorfält .

I kalkyl

Ytterligare information: Funktionskonceptets historik

Idén om funktion, som började på 1600-talet, var grundläggande för den nya infinitesimalkalkylen . Vid den tiden ansågs endast realvärderade funktioner av en reell variabel , och alla funktioner antogs vara jämna . Men definitionen utvidgades snart till funktioner av flera variabler och till funktioner av en komplex variabel . Under andra hälften av 1800-talet infördes den matematiskt rigorösa definitionen av en funktion, och funktioner med godtyckliga domäner och koddomäner definierades.

Funktioner används nu inom alla områden inom matematiken. I inledande kalkyl , när ordet funktion används utan förbehåll, betyder det en realvärderad funktion av en enda reell variabel. Den mer allmänna definitionen av en funktion introduceras vanligtvis för andra eller tredje års högskolestudenter med STEM- major, och under deras sista år introduceras de till kalkyl i en större, mer rigorös miljö i kurser som verklig analys och komplex analys .

Verklig funktion

Se även: Verklig analys

Graf över en linjär funktion

Graf över en polynomfunktion, här en kvadratisk funktion.

Graf över två trigonometriska funktioner: sinus och cosinus .

En reell funktion är en reellt värderad funktion av en reell variabel , det vill säga en funktion vars koddomän är fältet för reella tal och vars domän är en uppsättning reella siffror som innehåller ett intervall . I det här avsnittet kallas dessa funktioner helt enkelt för funktioner .

De funktioner som oftast betraktas i matematik och dess tillämpningar har viss regelbundenhet, det vill säga att de är kontinuerliga , differentierbara och till och med analytiska . Denna regelbundenhet säkerställer att dessa funktioner kan visualiseras av deras grafer . I det här avsnittet är alla funktioner differentierbara i ett visst intervall.

Funktioner åtnjuter punktvisa operationer , det vill säga om f och g är funktioner, är deras summa, skillnad och produkt funktioner som definieras av

${\begin{aligned}(f+g)(x)&=f(x)+g(x)\\(fg)(x)&=f(x)-g(x)\\( f\cdot g)(x)&=f(x)\cdot g(x)\\\end{aligned}}.$

Domänerna för de resulterande funktionerna är skärningspunkten mellan domänerna för f och g . Kvoten av två funktioner definieras på liknande sätt av

${\frac {f}{g}}(x)={\frac {f(x)}{g(x)}},$

men domänen för den resulterande funktionen erhålls genom att ta bort nollorna för g från skärningspunkten mellan domänerna för f och g .

Polynomfunktionerna definieras av polynom , och deras domän är hela uppsättningen av reella tal . De inkluderar konstantfunktioner , linjära funktioner och kvadratiska funktioner . Rationella funktioner är kvoter av två polynomfunktioner, och deras domän är de reella talen med ett ändligt antal av dem borttagna för att undvika division med noll . Den enklaste rationella funktionen är funktionen $x\mapsto {\frac {1}{x}},$ vars graf är en hyperbel och vars domän är hela den reella linjen förutom 0.

Derivatan av en reell differentierbar funktion är en reell funktion . En antiderivata av en kontinuerlig reell funktion är en reell funktion som har den ursprungliga funktionen som en derivata. Till exempel är funktionen $x\mapsto {\frac {1}{x}}$ kontinuerlig, och till och med differentierbar, på de positiva reella talen. En antiderivata, som tar värdet noll för x = 1 , är alltså en differentierbar funktion som kallas den naturliga logaritmen .

En reell funktion f är monoton i ett intervall om tecknet för ${\frac {f(x)-f(y)}{xy}}$ inte beror på av valet av x och y i intervallet. Om funktionen är differentierbar i intervallet är den monoton om derivatans tecken är konstant i intervallet. Om en reell funktion f är monoton i ett intervall I , har den an invers funktion , som är en reell funktion med domän f ( I ) och bild I. Så definieras inversa trigonometriska funktioner i termer av trigonometriska funktioner , där de trigonometriska funktionerna är monotona. Ett annat exempel: den naturliga logaritmen är monoton på de positiva reella talen, och dess bild är hela den reella linjen; därför har den en invers funktion som är en bijektion mellan de reella talen och de positiva reella talen. Denna invers är exponentialfunktionen .

Många andra reella funktioner definieras antingen av den implicita funktionssatsen (den inversa funktionen är en speciell instans) eller som lösningar av differentialekvationer . Till exempel sinus- och cosinusfunktionerna lösningarna för den linjära differentialekvationen

$y''+y=0$

Så att

$\sin 0=0,\quad \cos 0=1,\quad {\frac {\partial \sin x}{\partial x}}(0)=1,\quad {\frac {\partial \cos x}{\partial x}}(0)=0.$

Vektorvärderad funktion

Huvudartiklar: Vektorvärderad funktion och vektorfält

När elementen i en funktions koddomän är vektorer sägs funktionen vara en vektorvärderad funktion. Dessa funktioner är särskilt användbara i applikationer, till exempel modellering av fysiska egenskaper. Till exempel är funktionen som associerar till varje punkt i en vätska dess hastighetsvektor en vektorvärderad funktion.

Vissa vektorvärderade funktioner är definierade på en delmängd av $\mathbb {R} ^{n}$ eller andra utrymmen som delar geometriska eller topologiska egenskaper hos $\mathbb {R} ^{n}$ , såsom grenrör . Dessa vektorvärderade funktioner får namnet vektorfält .

Funktionsutrymme

Huvudartiklar: Funktionsutrymme och Funktionsanalys

I matematisk analys , och mer specifikt i funktionsanalys , är ett funktionsutrymme en uppsättning skalärvärdade eller vektorvärderade funktioner , som delar en specifik egenskap och bildar ett topologiskt vektorrum . Till exempel bildar de verkliga jämna funktionerna med ett kompakt stöd (det vill säga de är noll utanför någon kompakt uppsättning ) ett funktionsutrymme som ligger till grund för teorin om fördelningar .

Funktionsrum spelar en grundläggande roll i avancerad matematisk analys, genom att tillåta användning av deras algebraiska och topologiska egenskaper för att studera funktioners egenskaper. Till exempel är alla teorem om existens och unika lösningar av vanliga eller partiella differentialekvationer resultatet av studiet av funktionsrum.

Flervärdiga funktioner

Huvudartikel: Funktion med flera värden

Tillsammans bildar de två kvadratrötterna av alla icke-negativa reella tal en enda jämn kurva.

Flera metoder för att specificera funktioner för reella eller komplexa variabler utgår från en lokal definition av funktionen vid en punkt eller i ett område av en punkt, och utökar sedan genom kontinuitet funktionen till en mycket större domän. För en startpunkt $x_{0},$ finns det ofta flera möjliga startvärden för funktionen.

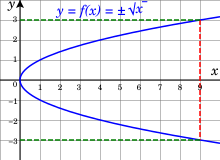
Till exempel, när du definierar kvadratroten som den inversa funktionen av kvadratfunktionen, för varje positivt reellt tal $x_{0},$ finns det två val för värdet av kvadratroten, varav ett är positivt och betecknas ${\sqrt {x_{0}}},$ och en annan som är negativ och betecknad $-{\sqrt {x_{0}}}.$ Dessa val definierar två kontinuerliga funktioner, som båda har de icke-negativa reella talen som en domän och har antingen de icke-negativa eller de icke-positiva reella talen som bilder. När man tittar på graferna för dessa funktioner kan man se att de tillsammans bildar en enda jämn kurva . Det är därför ofta användbart att betrakta dessa två kvadratrotsfunktioner som en enda funktion som har två värden för positivt x , ett värde för 0 och inget värde för negativt x .

I det föregående exemplet är det ena valet, den positiva kvadratroten, mer naturligt än det andra. Detta är inte fallet i allmänhet. Låt oss till exempel betrakta den implicita funktionen som mappar y till roten x av $x^{3}-3x-y=0$ (se bilden till höger). För y = 0 kan man välja $0,{\sqrt {3}},{\text{ eller }}-{\sqrt {3}}$ för x . Genom den implicita funktionssatsen definierar varje val en funktion; för den första är den (maximala) domänen intervallet [−2, 2] och bilden är [−1, 1] ; för den andra är domänen [−2, ∞) och bilden är [1, ∞) ; för den sista är domänen (−∞, 2] och bilden är (−∞, −1] . Eftersom de tre graferna tillsammans bildar en jämn kurva, och det inte finns någon anledning att föredra ett val, betraktas dessa tre funktioner ofta som en enda flervärdig funktion av y som har tre värden för −2 < y < 2 , och bara en värde för y ≤ −2 och y ≥ −2 .

Användbarheten av konceptet med flervärdiga funktioner är tydligare när man överväger komplexa funktioner, typiskt analytiska funktioner . Den domän till vilken en komplex funktion kan utvidgas genom analytisk fortsättning består i allmänhet av nästan hela det komplexa planet . Men när man utökar domänen genom två olika vägar får man ofta olika värden. Till exempel, när man utökar domänen för kvadratrotsfunktionen, längs en väg av komplexa tal med positiva imaginära delar, får man i för kvadratroten av −1; medan man, när man sträcker sig genom komplexa tal med negativa imaginära delar, får − i . Det finns i allmänhet två sätt att lösa problemet. Man kan definiera en funktion som inte är kontinuerlig längs någon kurva, som kallas en grensnitt . En sådan funktion kallas för funktionens huvudvärde . Det andra sättet är att anse att man har en funktion med flera värden , som är analytisk överallt förutom för isolerade singulariteter, men vars värde kan "hoppa" om man följer en sluten slinga runt en singularitet. Detta hopp kallas monodromin .

I grunderna för matematik och mängdlära

Definitionen av en funktion som ges i den här artikeln kräver begreppet set , eftersom domänen och koddomänen för en funktion måste vara en mängd. Detta är inget problem i vanlig matematik, eftersom det generellt sett inte är svårt att bara överväga funktioner vars domän och koddomän är uppsättningar, som är väldefinierade, även om domänen inte är explicit definierad. Men ibland är det bra att överväga mer allmänna funktioner.

Till exempel kan singeluppsättningen betraktas som en funktion $x\mapsto \{x\}.$ Dess domän skulle inkludera alla uppsättningar och skulle därför inte vara en uppsättning. I vanlig matematik undviker man den här typen av problem genom att ange en domän, vilket innebär att man har många singelfunktioner. Men när man etablerar grunder för matematik kan man behöva använda funktioner vars domän, koddomän eller båda inte är specificerade, och vissa författare, ofta logiker, ger en exakt definition för dessa svagt specificerade funktioner.

Dessa generaliserade funktioner kan vara avgörande för utvecklingen av en formalisering av matematikens grunder . Till exempel Von Neumann–Bernays–Gödel mängdlära , en förlängning av mängdläran där samlingen av alla mängder är en klass . Denna teori inkluderar ersättningsaxiomet , som kan anges som: Om X är en mängd och F är en funktion, så är F [ X ] en mängd.

I datavetenskap

Huvudartiklar: Funktion (datorprogrammering) och lambdakalkyl

Inom datorprogrammering är en funktion i allmänhet en del av ett datorprogram , som implementerar det abstrakta funktionsbegreppet. Det vill säga att det är en programenhet som producerar en utdata för varje ingång. Men i många programmeringsspråk kallas varje subrutin en funktion, även när det inte finns någon utdata, och när funktionaliteten helt enkelt består av att modifiera vissa data i datorns minne .

Funktionell programmering är programmeringsparadigmet som består av att bygga program genom att endast använda subrutiner som beter sig som matematiska funktioner. Till exempel, if_then_else är en funktion som tar tre funktioner som argument, och, beroende på resultatet av den första funktionen ( true eller false ), returnerar resultatet av antingen den andra eller den tredje funktionen. En viktig fördel med funktionell programmering är att den underlättar programbevis , eftersom den bygger på en välgrundad teori, lambdakalkylen ( se nedan).

Förutom datorspråkterminologi har "funktion" den vanliga matematiska betydelsen inom datavetenskap . I detta område är en egenskap av stort intresse en funktions beräkningsbarhet . För att ge en exakt innebörd till detta koncept, och till det relaterade begreppet algoritm , har flera beräkningsmodeller introducerats, de gamla är generella rekursiva funktioner , lambda-kalkyl och Turing-maskin . Grundsatsen för beräkningsteorin är att dessa tre beräkningsmodeller definierar samma uppsättning beräkningsbara funktioner, och att alla andra beräkningsmodeller som någonsin föreslagits definierar samma uppsättning beräkningsbara funktioner eller en mindre. Kyrkan -Turing-tesen är påståendet att varje filosofiskt godtagbar definition av en beräkningsbar funktion också definierar samma funktioner.

Allmänna rekursiva funktioner är partiella funktioner från heltal till heltal som kan definieras från

• konstanta funktioner ,
• efterträdare och
• projektionsfunktioner _

via operatörerna

• sammansättning ,
• primitiv rekursion , och
• minimering .

Även om de bara definieras för funktioner från heltal till heltal, kan de modellera vilken beräkningsbar funktion som helst som en konsekvens av följande egenskaper:

• en beräkning är manipulering av ändliga sekvenser av symboler (siffror i tal, formler, ...),
• varje sekvens av symboler kan kodas som en sekvens av bitar ,
• en bitsekvens kan tolkas som den binära representationen av ett heltal.

Lambdakalkyl är en teori som definierar beräkningsbara funktioner utan att använda mängdteori och är den teoretiska bakgrunden till funktionell programmering. Den består av termer som antingen är variabler, funktionsdefinitioner ( 𝜆 -termer) eller tillämpningar av funktioner på termer. Termer manipuleras genom vissa regler ( α -ekvivalensen, β -reduktionen och η -konverteringen), som är teorins axiom och kan tolkas som beräkningsregler.

I sin ursprungliga form inkluderar lambda-kalkyl inte begreppen domän och kodomän för en funktion. Grovt sett har de införts i teorin under namnet typ i maskinskriven lambdakalkyl . De flesta typer av maskinskrivna lambdakalkyler kan definiera färre funktioner än otypade lambdakalkyler.

Se även

Undersidor

• Lista över typer av funktioner
• Lista över funktioner
• Funktionsmontering
• Implicit funktion

Generaliseringar

• Funktion av högre ordning
• Homomorfism
• Morfism
• Mikrofunktion
• Distribution
• Funktionär

Relaterade ämnen

• Associativ array
• Uttryck i sluten form
• Elementär funktion
• Funktionell
• Funktionell nedbrytning
• Funktionellt predikat
• Funktionell programmering
• Parametrisk ekvation
• Ställ in funktion
• Enkel funktion

Källor

•    Bartle, Robert (1976). The Elements of Real Analysis (2nd ed.). Wiley. ISBN 978-0-471-05465-8 . OCLC 465115030 .
•   Bloch, Ethan D. (2011). Bevis och grunder: En första kurs i abstrakt matematik . Springer. ISBN 978-1-4419-7126-5 .
•   Cunningham, Daniel W. (2016). Mängdlära: En första kurs . Cambridge University Press. ISBN 978-1-107-12032-7 .
•   Gödel, Kurt (1940). Kontinuumhypotesens konsistens . Princeton University Press. ISBN 978-0-691-07927-1 .
•   Halmos, Paul R. (1970). Naiv mängdteori . Springer-Verlag. ISBN 978-0-387-90092-6 .
•   Jech, Thomas (2003). Mängdlära (3:e uppl.). Springer-Verlag . ISBN 978-3-540-44085-7 .
•   Spivak, Michael (2008). Calculus (4:e upplagan). Publicera eller förgås. ISBN 978-0-914098-91-1 .

Vidare läsning

•   Anton, Howard (1980). Kalkyl med analytisk geometri . Wiley . ISBN 978-0-471-03248-9 .
•   Bartle, Robert G. (1976). The Elements of Real Analysis (2nd ed.). Wiley. ISBN 978-0-471-05464-1 .
•   Dubinsky, Ed; Harel, Guershon (1992). Funktionsbegreppet: Aspekter av epistemologi och pedagogik . Mathematical Association of America. ISBN 978-0-88385-081-7 .
• Hammack, Richard (2009). "12. Funktioner" (PDF) . Bevisets bok . Virginia Commonwealth University . Hämtad 2012-08-01 .
• Husch, Lawrence S. (2001). Visuell kalkyl . University of Tennessee . Hämtad 2007-09-27 .
• Katz, Robert (1964). Axiomatisk analys . DC Heath and Company .
•    Kleiner, Israel (1989). "Funktionskonceptets utveckling: En kort undersökning". The College Mathematics Journal . 20 (4): 282–300. CiteSeerX 10.1.1.113.6352 . doi : 10.2307/2686848 . JSTOR 2686848 .
•   Lützen, Jesper (2003). "Mellan rigor och tillämpningar: Utveckling av funktionsbegreppet i matematisk analys" . I Porter, Roy (red.). The Cambridge History of Science: De moderna fysikaliska och matematiska vetenskaperna . Cambridge University Press. ISBN 978-0-521-57199-9 . En lättillgänglig och avledande historisk presentation.
• Malik, MA (1980). "Historiska och pedagogiska aspekter av definitionen av funktion". International Journal of Mathematical Education in Science and Technology . 11 (4): 489–492. doi : 10.1080/0020739800110404 .
•   Reichenbach, Hans (1947). Element av symbolisk logik . Dover. ISBN 0-486-24004-5 .
•   Ruthing, D. (1984). "Old Intelligencer: Några definitioner av funktionsbegreppet från Bernoulli, Joh. till Bourbaki, N.". Matematisk intelligens . 6 (4): 71–78. doi : 10.1007/BF03026743 . S2CID 189883712 .
•   Thomas, George B.; Finney, Ross L. (1995). Calculus and Analytic Geometry (9:e upplagan). Addison-Wesley . ISBN 978-0-201-53174-9 .

externa länkar

• "Function" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• Wolfram Functions Site ger formler och visualiseringar av många matematiska funktioner.
• NIST Digital Library of Mathematical Functions