Christiaan Huygens
|
Christiaan Huygens
| |
|---|---|

| |
| Född |
14 april 1629 |
| dog | 8 juli 1695 (66 år gammal) Haag, Nederländska republiken
|
| Alma mater | |
| Känd för | Lista
|
| Vetenskaplig karriär | |
| Fält | |
| institutioner | |
| Akademiska rådgivare | Frans van Schooten |
| Influenser | |
| Influerad | |
| Signatur | |
| Del av en serie om |
| klassisk mekanik |
|---|
Christiaan Huygens , Lord of Zeelhem , FRS ( / ˈ h aɪ ɡ ən z / hy -gənz , us också / ˈ h ɔɪ ɡ ɡ ɡ n z / hoy -gənz , holländska : [ˈkrɪstijaːn ˈɦœyɣə (n) s] ( ![]() lyssna ) ; också stavas Huyghens , latin : Hugenius , 14 april 1629 – 8 juli 1695) var en holländsk matematiker , fysiker , ingenjör , astronom och uppfinnare , som anses vara en av de viktigaste gestalterna i den vetenskapliga revolutionen . Inom fysiken gjorde Huygens viktiga bidrag till optik och mekanik , medan han som astronom är främst känd för sina studier av Saturnus ringar och upptäckten av dess måne Titan . Som ingenjör och uppfinnare förbättrade han designen av teleskop och uppfann pendelklockan, ett genombrott inom tidtagning och den mest exakta tidtagaren på nästan 300 år. En exceptionellt begåvad matematiker och fysiker, Huygens var den förste att idealisera ett fysiskt problem genom en uppsättning matematiska parametrar , och den första att helt matematisera en mekanistisk förklaring av ett oobserverbart fysiskt fenomen. Av dessa skäl har han kallats den första teoretiska fysikern och en av grundarna av modern matematisk fysik .
lyssna ) ; också stavas Huyghens , latin : Hugenius , 14 april 1629 – 8 juli 1695) var en holländsk matematiker , fysiker , ingenjör , astronom och uppfinnare , som anses vara en av de viktigaste gestalterna i den vetenskapliga revolutionen . Inom fysiken gjorde Huygens viktiga bidrag till optik och mekanik , medan han som astronom är främst känd för sina studier av Saturnus ringar och upptäckten av dess måne Titan . Som ingenjör och uppfinnare förbättrade han designen av teleskop och uppfann pendelklockan, ett genombrott inom tidtagning och den mest exakta tidtagaren på nästan 300 år. En exceptionellt begåvad matematiker och fysiker, Huygens var den förste att idealisera ett fysiskt problem genom en uppsättning matematiska parametrar , och den första att helt matematisera en mekanistisk förklaring av ett oobserverbart fysiskt fenomen. Av dessa skäl har han kallats den första teoretiska fysikern och en av grundarna av modern matematisk fysik .
Huygens identifierade först de korrekta lagarna för elastisk kollision i sitt verk De Motu Corporum ex Percussione , färdigt 1656 men publicerat postumt 1703. 1659 härledde Huygens geometriskt formeln i klassisk mekanik för centrifugalkraften i sitt verk De vi Centrifuga , en decennium före Newton . Inom optiken är han mest känd för sin vågteori om ljus, som han beskrev i sin Traité de la Lumière (1690). Hans teori om ljus förkastades initialt till förmån för Newtons korpuskulära teori om ljus , tills Augustin-Jean Fresnel antog Huygens princip för att ge en fullständig förklaring av ljusets rätlinjiga utbredning och diffraktionseffekter 1821. Idag är denna princip känd som Huygens– Fresnelprincipen .
Huygens uppfann pendelklockan 1657, som han patenterade samma år. Hans horologiska forskning resulterade i en omfattande analys av pendeln i Horologium Oscillatorium (1673), betraktad som ett av de viktigaste 1600-talsverken om mekanik. Även om den innehåller beskrivningar av klockdesigner, är det mesta av boken en analys av pendulrörelser och en teori om kurvor . År 1655 började Huygens slipa linser med sin bror Constantijn för att bygga brytande teleskop . Han upptäckte den första av Saturnus månar, Titan, och var den första som förklarade Saturnus märkliga utseende på grund av "en tunn, platt ring, som inte rörde någonstans och lutade mot ekliptikan." År 1662 utvecklade Huygens det som nu kallas Huygenian-okularet , ett teleskop med två linser för att minska mängden spridning .
Som matematiker utvecklade Huygens teorin om evolutes och skrev om hasardspel och problem med poäng i Van Rekeningh i Spelen van Gluck , som Frans van Schooten översatte och publicerade som De Ratiociniis i Ludo Aleae (1657). Användningen av förväntningsvärden av Huygens och andra skulle senare inspirera Jacob Bernoullis arbete med sannolikhetsteori .
Biografi

Christiaan Huygens föddes den 14 april 1629 i Haag , i en rik och inflytelserik holländsk familj, den andra sonen till Constantijn Huygens . Christiaan fick sitt namn efter sin farfar. Hans mor, Suzanna van Baerle , dog kort efter att ha fött Huygens syster. Paret fick fem barn: Constantijn (1628), Christiaan (1629), Lodewijk (1631), Philips (1632) och Suzanna (1637).
Constantijn Huygens var diplomat och rådgivare till House of Orange , förutom att vara poet och musiker. Han korresponderade brett med intellektuella över hela Europa; hans vänner inkluderade Galileo Galilei , Marin Mersenne och René Descartes . Christiaan utbildades hemma fram till sexton års ålder och gillade från unga år att leka med miniatyrer av kvarnar och andra maskiner. Från sin far fick han en liberal utbildning och studerade språk, musik , historia , geografi , matematik , logik och retorik , tillsammans med dans , fäktning och ridning .
År 1644 hade Huygens som sin matematiska handledare Jan Jansz Stampioen , som tilldelade 15-åringen en krävande litteraturlista om samtida vetenskap. Descartes blev senare imponerad av sina färdigheter i geometri, liksom Mersenne, som döpte honom till "den nye Arkimedes ."
Studentår
Vid sexton års ålder skickade Constantijn Huygens för att studera juridik och matematik vid Leiden University , där han studerade från maj 1645 till mars 1647. Frans van Schooten var akademiker i Leiden från 1646 och blev privatlärare till Huygens och hans äldre bror , Constantijn Jr., ersätter Stampioen på inrådan av Descartes. Van Schooten förde Huygens matematiska utbildning aktuell, introducera honom till arbetet med Viète , Descartes och Fermat .
Efter två år, med början i mars 1647, fortsatte Huygens sina studier vid det nygrundade Orange College i Breda , där hans far var kurator . Constantijn Huygens var nära involverad i det nya kollegiet, som varade endast till 1669; rektor var André Rivet . Christiaan Huygens bodde hemma hos juristen Johann Henryk Dauber medan han gick på college, och hade matematikklasser med den engelska lektorn John Pell . Hans tid i Breda slutade vid den tidpunkt då hans bror Lodewijk, som var inskriven på skolan, duellerade med en annan elev. Huygens lämnade Breda efter att ha avslutat sina studier i augusti 1649 och hade en period som diplomat på ett uppdrag med Henrik, hertig av Nassau . Det tog honom till Bentheim , sedan Flensburg . Han lyfte till Danmark, besökte Köpenhamn och Helsingör och hoppades kunna korsa Öresund för att besöka Descartes i Stockholm . Det fick det inte bli.
Även om hans far Constantijn hade önskat att hans son Christiaan skulle bli diplomat, hindrade omständigheterna honom från att bli det. Den första Stadtholderless-perioden som började 1650 innebar att House of Orange inte längre hade makten, vilket tog bort Constantijns inflytande. Vidare insåg han att hans son inte hade något intresse av en sådan karriär.
Tidig korrespondens
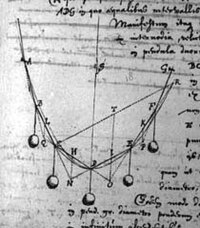
Huygens skrev i allmänhet på franska eller latin. 1646, medan han fortfarande var högskolestudent i Leiden, började han en korrespondens med sin fars vän, Marin Mersenne , som dog kort därefter 1648. Mersenne skrev till Constantijn om sin sons talang för matematik och jämförde honom smickrande med Archimedes den 3 januari. 1647.
Bokstäverna visar Huygens tidiga intresse för matematik. I oktober 1646 finns hängbron och demonstrationen att en hängande kedja inte är en parabel , som Galileo trodde. Huygens skulle senare märka den kurvan catenaria ( kontaktledning ) 1690 samtidigt som han motsvarade Gottfried Leibniz .
Under de följande två åren (1647-48) täckte Huygens brev till Mersenne olika ämnen, inklusive ett matematiskt bevis på lagen om fritt fall , påståendet från Grégoire de Saint-Vincent om cirkelkvadratur , vilket Huygens visade vara fel, rättelse av ellipsen, projektiler och den vibrerande strängen . Några av Mersennes bekymmer vid den tiden, såsom cykloiden ( han skickade Huygens Torricellis avhandling om kurvan), svängningscentrum och gravitationskonstanten , var frågor Huygens tog på allvar först mot slutet av 1600-talet. Mersenne hade också skrivit om musikteori. Huygens föredrog medeltonstemperament ; han förnyade i 31 lika temperament (vilket i sig inte var en ny idé men känt för Francisco de Salinas ), med hjälp av logaritmer för att undersöka det vidare och visa dess nära relation till medeltonsystemet.
År 1654 återvände Huygens till sin fars hus i Haag, och kunde ägna sig helt åt forskning. Familjen hade ett annat hus, inte långt borta vid Hofwijck , och han tillbringade tid där under sommaren. Trots att han var mycket aktiv tillät hans akademiska liv honom inte att undkomma anfall av depression.
Därefter utvecklade Huygens ett brett spektrum av korrespondenter, även om det hämmades av den femåriga Fronde i Frankrike att ta upp trådarna efter 1648. När han besökte Paris 1655 bad Huygens Ismael Boulliau att presentera sig, som tog honom till Claude Mylon . Den parisiska gruppen av savanter som hade samlats runt Mersenne höll ihop in på 1650-talet, och Mylon, som hade tagit på sig sekreterarrollen, gjorde lite besvär för att hålla Huygens i kontakt. Genom Pierre de Carcavi korresponderade Huygens 1656 med Pierre de Fermat, som han beundrade mycket, även om denna sida av avgudadyrkan. Erfarenheten var bitterljuv och något förbryllande, eftersom det stod klart att Fermat hade hoppat av huvudfåran i forskningen, och hans prioriterade anspråk kunde förmodligen inte gottgöras i vissa fall. Dessutom letade Huygens då efter att tillämpa matematik på fysiken, medan Fermats bekymmer gick till renare ämnen.
Vetenskaplig debut

Liksom några av hans samtida var Huygens ofta långsam med att begå sina resultat och upptäckter på tryck, och föredrar att sprida sitt arbete genom brev istället. Under sina tidiga dagar gav hans mentor Frans van Schooten teknisk feedback och var försiktig för sitt ryktes skull.
Mellan 1651 och 1657 publicerade Huygens ett antal verk som visade hans talang för matematik och hans behärskning av både klassisk och analytisk geometri , vilket ökade hans räckvidd och rykte bland matematiker. Ungefär samtidigt började Huygens ifrågasätta Descartes kollisionslagar, som till stor del var felaktiga, och härledde de korrekta lagarna algebraiskt och senare genom geometri. Han visade att, för alla system av kroppar, förblir systemets tyngdpunkt densamma i hastighet och riktning, vilket Huygens kallade bevarandet av "rörelsekvantitet" . Medan andra studerade påverkan ungefär samtidigt, var Huygens teori om kollisioner mer generell. Dessa resultat var kända genom korrespondens och i en kort artikel i Journal des Sçavans men skulle förbli i stort sett opublicerade till efter hans död, med publiceringen av De Motu Corporum ex Percussione ( Angående rörelsen av kolliderande kroppar ).
Utöver sitt arbete med mekanik gjorde han viktiga vetenskapliga upptäckter, såsom identifieringen av Saturnus måne Titan 1655 och uppfinningen av pendelklockan 1657, som båda gav honom berömmelse över hela Europa. Den 3 maj 1661 observerade Huygens planeten Merkurius passera över solen med hjälp av instrumentmakaren Richard Reeves teleskop i London, tillsammans med astronomen Thomas Streete och Reeve. Streete diskuterade sedan det publicerade rekordet av Hevelius transitering, en kontrovers förmedlad av Henry Oldenburg . Huygens överlämnade till Hevelius ett manuskript av Jeremiah Horrocks på Venus transitering, 1639, som trycktes för första gången 1662.
Sir Robert Moray skickade Huygens John Graunts livstabell 1662 , och med tiden ägnade Huygens och hans bror Lodewijk sig till den förväntade livslängden . Huygens skapade så småningom den första grafen av en kontinuerlig distributionsfunktion under antagandet om en enhetlig dödsfrekvens och använde den för att lösa problem i gemensamma livräntor . Samma år intresserade Huygens, som spelade cembalo , Simon Stevins teorier om musik; dock visade han mycket lite oro för att publicera sina teorier om konsonans , av vilka några gick förlorade i århundraden. För sina bidrag till vetenskapen Royal Society of London Huygens till en stipendiat 1665, vilket gjorde honom till dess första utländska medlem när han bara var 36 år gammal.
Frankrike

Montmor Academy var den form den gamla Mersenne-kretsen tog efter mitten av 1650-talet. Huygens deltog i dess debatter och stödde dess "oliktänkande" fraktion som förespråkade experimentell demonstration för att begränsa fruktlös diskussion och motsatte sig amatörmässiga attityder. Under 1663 gjorde han vad som var hans tredje besök i Paris; Montmor Academy lades ner, och Huygens tog chansen att förespråka ett mer baconiskt program inom vetenskap. Tre år senare, 1666, flyttade han till Paris på en inbjudan att fylla en tjänst vid kung Ludvig XIV: s nya franska Académie des sciences .
Medan han var i Paris hade Huygens en viktig beskyddare och korrespondent i Jean-Baptiste Colbert , Ludvig XIV:s förste minister. Hans förhållande till den franska akademin var dock inte alltid lätt, och 1670 valde Huygens, allvarligt sjuk, Francis Vernon att donera sina papper till Royal Society i London, om han skulle dö. Efterdyningarna av det fransk-holländska kriget (1672–78), och särskilt Englands roll i det, kan ha skadat hans förhållande till Royal Society. Robert Hooke , som representant för Royal Society, saknade finess för att hantera situationen 1673.
Fysikern och uppfinnaren Denis Papin var assistent till Huygens från 1671. Ett av deras projekt, som inte gav direkt frukt, var krutmotorn . Papin flyttade till England 1678 för att fortsätta arbeta inom detta område. Också i Paris gjorde Huygens ytterligare astronomiska observationer med hjälp av observatoriet som nyligen färdigställdes 1672. Han introducerade Nicolaas Hartsoeker för franska vetenskapsmän som Nicolas Malebranche och Giovanni Cassini 1678.
Huygens träffade Leibniz som ung diplomat och besökte Paris 1672 på ett fåfängt uppdrag för att träffa den franske utrikesministern Arnauld de Pomponne . Vid denna tidpunkt arbetade Leibniz på en räknemaskin , och han flyttade till London i början av 1673 med diplomater från Mainz . Från mars 1673 undervisades Leibniz i matematik av Huygens, som lärde honom analytisk geometri. En omfattande korrespondens följde, där Huygens till en början visade ovilja att acceptera fördelarna med Leibniz infinitesimalkalkyl .
Sista åren
Huygens flyttade tillbaka till Haag 1681 efter att ha drabbats av ytterligare en anfall av allvarlig depressiv sjukdom. År 1684 publicerade han Astroscopia Compendiaria på sitt nya tublösa luftteleskop . Han försökte återvända till Frankrike 1685 men upphävandet av Ediktet av Nantes uteslöt detta drag. Hans far dog 1687 och han ärvde Hofwijck, som han gjorde till sitt hem året därpå.
På sitt tredje besök i England träffade Huygens Isaac Newton personligen den 12 juni 1689. De talade om Island spar och korresponderade därefter om motståndsrörelse.
Huygens återvände till matematiska ämnen under sina sista år och observerade det akustiska fenomen som nu kallas flänsning 1693. Två år senare, den 8 juli 1695, dog Huygens i Haag och begravdes i en omärkt grav i Grote Kerk där, liksom hans far före honom.
Huygens gifte sig aldrig.
Matematik
Huygens blev först internationellt känd för sitt arbete inom matematik och publicerade ett antal viktiga resultat som uppmärksammades av många europeiska geometrar. Huygens föredragna metod i hans publicerade verk var Archimedes, även om han använde Descartes analytiska geometri och Fermats infinitesimala tekniker mer utförligt i sina privata anteckningsböcker.
Publicerade verk
Theoremata de Quadratura

Huygens första publikation var Theoremata de Quadratura Hyperboles, Ellipsis et Circuli ( Theorems on the quadrature of the hyperbola, ellips and circle ), utgiven av Elzeviers i Leiden 1651. Den första delen av arbetet innehöll satser för beräkning av hyperbolernas arealer , ellipser och cirklar som parallellt med Arkimedes arbete med koniska sektioner, särskilt hans Quadrature of the Parabola . Den andra delen inkluderade ett vederläggande av Grégoire de Saint-Vincents påståenden om cirkelkvadratur, som han hade diskuterat med Mersenne tidigare.
Huygens visade att tyngdpunkten för ett segment av någon hyperbel , ellips eller cirkel var direkt relaterad till området för det segmentet. Han kunde sedan visa sambanden mellan trianglar inskrivna i koniska sektioner och tyngdpunkten för dessa sektioner. Genom att generalisera dessa satser till alla koniska sektioner utökade Huygens klassiska metoder för att generera nya resultat.
Kvadratur var en levande fråga på 1650-talet och genom Mylon ingrep Huygens i diskussionen om matematiken hos Thomas Hobbes . Genom att envisas med att försöka förklara felen Hobbes hade hamnat i, skapade han ett internationellt rykte.
De Circuli Magnitudine Inventa
Huygens nästa publikation var De Circuli Magnitudine Inventa ( Nya fynd i mätningen av cirkeln ), publicerad 1654. I detta arbete kunde Huygens minska klyftan mellan de omskrivna och inskrivna polygonerna som finns i Archimedes' Mätning av cirkeln , vilket visar att förhållandet mellan omkretsen och dess diameter eller π måste ligga i den första tredjedelen av det intervallet.
Genom att använda en teknik som motsvarar Richardsons extrapolering kunde Huygens förkorta de ojämlikheter som användes i Archimedes metod; i detta fall, genom att använda tyngdpunkten för ett segment av en parabel, kunde han approximera tyngdpunkten för ett segment av en cirkel, vilket resulterade i en snabbare och exakt approximation av cirkelkvadraturen. Från dessa satser erhöll Huygens två uppsättningar värden för π : den första mellan 3,1415926 och 3,1415927, och den andra mellan 3,1415926538 och 3,1415926533.
Huygens visade också att, i fallet med hyperbeln , producerar samma approximation med paraboliska segment en snabb och enkel metod för att beräkna logaritmer . Han bifogade en samling av lösningar på klassiska problem i slutet av arbetet under titeln Illustrium Quorundam Problematum Constructiones ( Construction of some illustrious problems) .
De Ratiociniis i Ludo Aleae
Huygens blev intresserad av hasardspel efter att han besökte Paris 1655 och stötte på verk av Fermat, Blaise Pascal och Girard Desargues år tidigare. Han publicerade så småningom vad som vid den tiden var den mest sammanhängande presentationen av ett matematiskt förhållningssätt till hasardspel i De Ratiociniis i Ludo Aleae ( Om resonemang i hasardspel ). Frans van Schooten översatte det ursprungliga holländska manuskriptet till latin och publicerade det i sin Exercitationum Mathematicarum (1657).
Arbetet innehåller tidiga spelteoretiska idéer och behandlar särskilt problemet med poäng . Huygens tog från Pascal begreppen "rättvist spel" och rättvist kontrakt (dvs lika delning när chanserna är lika), och utökade argumentet till att sätta upp en icke-standardiserad teori om förväntade värden. Hans framgång med att tillämpa algebra på slumpens rike, som hittills verkade otillgänglig för matematiker, visade kraften i att kombinera euklidiska syntetiska bevis med det symboliska resonemang som finns i Viète och Descartes verk.
Huygens inkluderade fem utmanande problem i slutet av boken som blev standardtestet för alla som vill visa sin matematiska skicklighet i hasardspel under de kommande sextio åren. Människor som arbetade med dessa problem var Abraham de Moivre , Jacob Bernoulli, Johannes Hudde , Baruch Spinoza och Leibniz.
Opublicerat verk

Huygens hade tidigare färdigställt ett manuskript på samma sätt som Archimedes On Floating Bodies med titeln De Iis quae Liquido Supernatant ( Om delar som flyter ovanför vätskor ). Den skrevs omkring 1650 och bestod av tre böcker. Även om han skickade det färdiga verket till Frans van Schooten för feedback, valde Huygens till slut att inte publicera det och föreslog vid ett tillfälle att det skulle brännas. Några av resultaten som hittats här återfanns inte förrän på artonde och artonde århundradena.
Huygens återhämtar först Archimedes resultat för sfärens och paraboloidens stabilitet genom en smart tillämpning av Torricellis princip (dvs att kroppar i ett system rör sig endast om deras tyngdpunkt sjunker). Han bevisar sedan den allmänna satsen att för en flytande kropp i jämvikt är avståndet mellan dess tyngdpunkt och dess nedsänkta del på ett minimum. Huygens använder detta teorem för att komma fram till ursprungliga lösningar för stabiliteten hos flytande koner , parallellepipeder och cylindrar , i vissa fall genom en hel rotationscykel. Hans tillvägagångssätt var alltså likvärdigt med principen om virtuellt arbete . Huygens var också den första att inse att för homogena fasta ämnen är deras specifika vikt och bildförhållande de väsentliga parametrarna för hydrostatisk stabilitet .
Naturfilosofi
Huygens var den ledande europeiska naturfilosofen mellan Descartes och Newton. Emellertid, till skillnad från många av sina samtida, hade Huygens ingen smak för storslagna teoretiska eller filosofiska system och undvek i allmänhet att ta itu med metafysiska frågor (om påtryckt höll han sig till sin tids kartesiska och mekaniska filosofi ). Istället utmärkte Huygens sig i att utöka sina föregångares arbete, såsom Galileo, för att härleda lösningar på olösta fysiska problem som var mottagliga för matematisk analys. I synnerhet sökte han förklaringar som förlitade sig på kontakt mellan kroppar och undvek handling på avstånd .
I likhet med Robert Boyle och Jacques Rohault förespråkade Huygens en experimentellt orienterad, korpuskulär-mekanisk naturfilosofi under sina år i Paris. Detta tillvägagångssätt kallades ibland "Baconian", utan att vara induktivistisk eller identifiera sig med Francis Bacons åsikter på ett enkelt sätt.
Efter sitt första besök i England 1661 och när han deltog i ett möte på Gresham College där han lärde sig direkt om Boyles luftpumpsexperiment , tillbringade Huygens tid i slutet av 1661 och början av 1662 med att replikera arbetet. Det visade sig vara en lång process som förde upp till ytan både en experimentell fråga ("anomal suspension") och en teoretisk fråga (" horror vacui ") och som slutade i juli 1663 när Huygens blev medlem av Royal Society. Huygens kom att acceptera Boyles syn på tomrummet mot det kartesiska förnekandet av det, medan replikeringen av resultaten av Boyles experiment med luftpumpen slutade stökigt.
Newtons inflytande på John Locke förmedlades av Huygens, som försäkrade Locke att Newtons matematik var sund, vilket ledde till Lockes acceptans av en korpuskulär-mekanisk fysik.
Lagar för rörelse, stötar och gravitation

Det allmänna tillvägagångssättet för de mekaniska filosoferna var att postulera teorier av det slag som nu kallas "kontakthandling". Huygens anammade denna metod, men inte utan att ha sett dess svårigheter och misslyckanden. Leibniz, hans student i Paris, övergav senare teorin. Att se universum på detta sätt gjorde teorin om kollisioner central för fysiken. Materia i rörelse utgjorde universum, och endast förklaringar i dessa termer kunde vara riktigt begripliga. Medan han var influerad av det kartesiska förhållningssättet var han mindre doktrinär. Han studerade elastiska kollisioner på 1650-talet men försenade publiceringen i över ett decennium.
Huygens drog ganska tidigt slutsatsen att Descartes lagar för elastisk kollision mellan två kroppar måste vara felaktiga, och han formulerade de korrekta lagarna, inklusive bevarandet av produkten av massa gånger kvadraten av hastigheten för hårda kroppar, och bevarandet av kvantiteten av rörelse. i en riktning för alla kroppar. Ett viktigt steg var hans erkännande av den galileiska invariansen av problemen. Huygens hade faktiskt utarbetat kollisionslagarna från 1652 till 1656 i ett manuskript med titeln De Motu Corporum ex Percussione, även om hans resultat tog många år att cirkulera. 1661 vidarebefordrade han dem personligen till William Brouncker och Christopher Wren i London. Det som Spinoza skrev till Henry Oldenburg om dem 1666, under det andra anglo-holländska kriget, bevakades. Kriget slutade 1667 och Huygens tillkännagav sina resultat för Royal Society 1668. Han publicerade dem senare i Journal des Sçavans 1669.
gravitationsaccelerationens konstant och angav vad som nu är känt som den andra av Newtons rörelselagar i kvadratisk form. Han härledde geometriskt den numera standardformeln för centrifugalkraften , som utövas på ett föremål när det ses i en roterande referensram, till exempel när man kör runt en kurva. I modern notation:
med m objektets massa , w vinkelhastigheten och r radien . _ _ Huygens samlade sina resultat i en avhandling under titeln De vi Centrifuga , opublicerad fram till 1703, där kinematik av fritt fall användes för att producera den första generaliserade uppfattningen om kraft före Newton. Den allmänna formeln för centrifugalkraften publicerades dock 1673 och var ett viktigt steg i att studera omloppsbanor inom astronomi. Det möjliggjorde övergången från Keplers tredje lag för planetrörelse till den omvända kvadratiska gravitationslagen. Ändå skilde Huygens tolkning av Newtons arbete om gravitation från Newtonianernas som Roger Cotes : han insisterade inte på Descartes a priori attityd, men han skulle inte heller acceptera aspekter av gravitationsattraktioner som i princip inte kunde tillskrivas kontakt mellan partiklar.
Det tillvägagångssätt som används av Huygens saknade också några centrala föreställningar om matematisk fysik, som inte gick förlorade för andra. I sitt arbete med pendlar kom Huygens mycket nära teorin om enkel harmonisk rörelse ; ämnet täcktes dock helt för första gången av Newton i bok II av Principia Mathematica (1687). 1678 plockade Leibniz ut idén om bevarandelagar som Huygens hade lämnat implicit från Huygens arbete med kollisioner.
Horologi
Pendelur

1657, inspirerad av tidigare forskning om pendlar som regleringsmekanismer, uppfann Huygens pendelklockan, som var ett genombrott inom tidtagning och blev den mest exakta tidtagaren i nästan 300 år fram till 1930-talet. Pendelklockan var mycket mer exakt än de befintliga kant- och foliotklockorna och blev omedelbart populär och spred sig snabbt över Europa. Han anlitade konstruktionen av sina klockdesigner till Salomon Coster i Haag, som byggde klockan. Huygens tjänade dock inte mycket pengar på sin uppfinning. Pierre Séguier vägrade honom några franska rättigheter, medan Simon Douw i Rotterdam och Ahasverus Fromanteel i London kopierade hans design 1658. Den äldsta kända pendelklockan i Huygens-stil är daterad 1657 och kan ses på Museum Boerhaave i Leiden .
En del av incitamentet för att uppfinna pendelklockan var att skapa en exakt marin kronometer som kunde användas för att hitta longitud genom himmelsnavigering under havsresor. Klockan visade sig dock misslyckas som marin tidtagare eftersom skeppets gungande rörelse störde pendelns rörelse. År 1660 gjorde Lodewijk Huygens en rättegång på en resa till Spanien och rapporterade att det tunga vädret gjorde klockan värdelös. Alexander Bruce armbågade in på fältet 1662, och Huygens kallade in Sir Robert Moray och Royal Society för att medla och bevara några av hans rättigheter. Rättegångar fortsatte in på 1660-talet, de bästa nyheterna kom från en kapten från den kungliga flottan Robert Holmes som opererade mot de holländska besittningarna 1664. Lisa Jardine tvivlar på att Holmes rapporterade resultaten av rättegången korrekt, eftersom Samuel Pepys uttryckte sina tvivel vid den tiden.
En rättegång för Franska Akademien på en expedition till Cayenne slutade illa. Jean Richer föreslog korrigering för jordens figur . Vid tiden för det holländska Ostindiska kompaniets expedition 1686 till Godahoppsudden, kunde Huygens tillhandahålla korrigeringen i efterhand.
Horologium Oscillatorium
Sexton år efter uppfinningen av pendelklockan, 1673, publicerade Huygens sitt huvudverk om urologi med titeln Horologium Oscillatorium: Sive de Motu Pendulorum ad Horologia Aptato Demonstrationes Geometricae ( Pendelklockan: eller geometriska demonstrationer om pendlars rörelse som tillämpas på klockor ). Det är det första moderna arbetet om mekanik där ett fysiskt problem idealiseras av en uppsättning parametrar som sedan analyseras matematiskt.
Huygens motivation kom från observationen, gjord av Mersenne och andra, att pendlar inte är helt isokrona : deras period beror på deras svingbredd, med breda gungor som tar något längre än smala gungor. Han tacklade detta problem genom att hitta kurvan nedåt som en massa kommer att glida under inverkan av gravitationen under samma tid, oavsett dess utgångspunkt; det så kallade tautochrone problemet . Genom geometriska metoder som förutsåg kalkylen , visade Huygens att det var en cykloid snarare än den cirkulära bågen av en pendel, och därför att pendlar behövde röra sig på en cykloidbana för att vara isokrona. Den matematik som krävs för att lösa detta problem ledde Huygens att utveckla sin teori om evolutes, som han presenterade i del III av hans Horologium Oscillatorium .
Han löste också ett problem som ställts av Mersenne tidigare: hur man beräknar perioden för en pendel gjord av en godtyckligt formad svängande stel kropp. Detta innebar att upptäcka svängningscentrum och dess ömsesidiga förhållande till vridpunkten. I samma arbete analyserade han den koniska pendeln , bestående av en vikt på en lina som rörde sig i en cirkel, med hjälp av begreppet centrifugalkraft.
Huygens var den första som härledde formeln för perioden för en idealisk matematisk pendel (med massalös stång eller snöre och längd mycket längre än dess sving), i modern notation:
med T perioden, l pendelns längd och g gravitationsaccelerationen . Genom sin studie av svängningsperioden för sammansatta pendlar gjorde Huygens avgörande bidrag till utvecklingen av begreppet tröghetsmoment .
Huygens observerade också kopplade svängningar : två av hans pendelklockor monterade bredvid varandra på samma stöd blev ofta synkroniserade och svängde i motsatta riktningar. Han rapporterade resultaten per brev till Royal Society, och det hänvisas till som " en udda sorts sympati " i sällskapets protokoll. Detta koncept är nu känt som entrainment .
Balans vårklocka
1675, medan han undersökte cykloidens oscillerande egenskaper, kunde Huygens omvandla en cykloidpendel till en vibrerande fjäder genom en kombination av geometri och högre matematik. Samma år designade Huygens en spiralbalansfjäder och patenterade ett fickur . Dessa klockor är kända för att sakna en säkring för att utjämna huvudfjäderns vridmoment. Innebörden är att Huygens trodde att hans spiralfjäder skulle isokronisera balansen på samma sätt som cykloidformade upphängningskanter på hans klockor skulle isokronisera pendeln.
Han använde senare spiralfjädrar i mer konventionella klockor, gjorda för honom av Thuret i Paris. Sådana fjädrar är nödvändiga i moderna klockor med en fristående spak escapement eftersom de kan justeras för isokronism . Klockor på Huygens tid använde dock den mycket ineffektiva kantrymningen , som störde de isokrona egenskaperna hos någon form av balansfjäder, spiral eller annat.
Huygens design kom ungefär samtidigt som, men oberoende av, Robert Hookes. Kontroversen om prioriteringen av balansfjädern höll i sig i århundraden. I februari 2006 upptäcktes en sedan länge borttappad kopia av Hookes handskrivna anteckningar från flera decennier av Royal Society-möten i ett skåp i Hampshire , England, vilket antagligen visade bevisen till Hookes fördel.
Optik
Dioptri
Huygens hade ett långsiktigt intresse för studiet av ljusbrytning och linser eller dioptri . Från 1652 daterar de första utkasten till en latinsk avhandling om teorin om dioptri, känd som Tractatus , som innehöll en omfattande och rigorös teori om teleskopet. Huygens var en av få som väckte teoretiska frågor angående teleskopets egenskaper och funktion, och nästan den enda som riktade sin matematiska kunskap mot de faktiska instrument som används inom astronomi.
Huygens tillkännagav upprepade gånger dess publicering för sina kollegor men sköt till slut upp den till förmån för en mycket mer omfattande behandling, nu under namnet Dioptrica . Den bestod av tre delar. Den första delen fokuserade på de allmänna principerna för brytning, den andra behandlade sfärisk och kromatisk aberration , medan den tredje täckte alla aspekter av konstruktionen av teleskop och mikroskop. I motsats till Descartes dioptri som endast behandlade idealiska (elliptiska och hyperboliska) linser, sysslade Huygens uteslutande med sfäriska linser, som var den enda sorten som verkligen kunde tillverkas och inkorporeras i anordningar som mikroskop och teleskop.
Huygens utarbetade också praktiska sätt att minimera effekterna av sfärisk och kromatisk aberration, såsom långa brännvidd för objektivet i ett teleskop, interna stopp för att minska bländaren och en ny typ av okulär i form av en uppsättning av två planokonvexa linser, nu kända som Huygens okular. Dioptrica publicerades aldrig under Huygens livstid och publicerades först 1703, när det mesta av dess innehåll redan var bekant för den vetenskapliga världen .
Linser
Tillsammans med sin bror Constantijn började Huygens slipa sina egna linser 1655 i ett försök att förbättra teleskop. Han designade 1662 det som nu kallas Huygenian-okularet , med två linser, som ett teleskopokulär. Linser var också ett gemensamt intresse genom vilket Huygens kunde träffas socialt på 1660-talet med Spinoza, som grundade dem professionellt. De hade ganska olika syn på vetenskap, Spinoza var den mer engagerade kartesianen, och en del av deras diskussioner överlever i korrespondens. Antoni van Leeuwenhoeks arbete , en annan linskvarn, inom mikroskopi som intresserade hans far.
Huygens undersökte också användningen av linser i projektorer. Han krediteras som uppfinnaren av den magiska lyktan , beskriven i korrespondens från 1659. Det finns andra till vilka en sådan lyktaanordning har tillskrivits, såsom Giambattista della Porta och Cornelis Drebbel , även om Huygens design använde lins för bättre projektion ( Athanasius Kircher har också krediterats för det).
Traité de la Lumière

Huygens är särskilt ihågkommen inom optiken för sin vågteori om ljus, som han först kommunicerade 1678 till Académie des sciences i Paris. Ursprungligen ett preliminärt kapitel av hans Dioptrica , Huygens teori publicerades 1690 under titeln Traité de la Lumière ( Avhandling om ljus ), och innehåller den första helt matematiserade, mekanistiska förklaringen av ett oobserverbart fysiskt fenomen (dvs ljusutbredning). Huygens hänvisar till Ignace-Gaston Pardies , vars manuskript om optik hjälpte honom med hans vågteori.
Utmaningen vid den tiden var att förklara geometrisk optik , eftersom de flesta fysiska optikfenomen (som diffraktion ) inte hade observerats eller uppskattats som problem. Huygens hade experimenterat 1672 med dubbelbrytning ( dubbelbrytning ) i islandsspåren (en kalcit ), ett fenomen som upptäcktes 1669 av Rasmus Bartholin . Till en början kunde han inte belysa vad han hittade men kunde senare förklara det med sin vågfrontsteori och begreppet evolutes. Han utvecklade också idéer om kaustik . Huygens antar att ljusets hastighet är ändlig, baserat på en rapport av Ole Christensen Rømer 1677 men som Huygens antas redan ha trott. Huygens teori förutsätter ljus som utstrålande vågfronter , med den vanliga föreställningen om ljusstrålar som visar utbredning normal till dessa vågfronter. Utbredningen av vågfronterna förklaras sedan som resultatet av att sfäriska vågor emitteras vid varje punkt längs vågfronten (i dag känd som Huygens–Fresnel-principen). Det antog en allestädes närvarande eter , med överföring genom perfekt elastiska partiklar, en revidering av synen på Descartes. Ljusets natur var därför en longitudinell våg .
Hans teori om ljus var inte allmänt accepterad, medan Newtons rivaliserande korpuskulära teori om ljus , som finns i hans Opticks (1704), fick mer stöd. En stark invändning mot Huygens teori var att longitudinella vågor bara har en enda polarisation som inte kan förklara den observerade dubbelbrytningen. Men Thomas Youngs interferensexperiment 1801 och François Aragos upptäckt av Poisson-fläcken 1819 kunde inte förklaras genom Newtons eller någon annan partikelteori, vilket återupplivade Huygens idéer och vågmodeller. Fresnel blev medveten om Huygens arbete och kunde 1821 förklara dubbelbrytning som ett resultat av att ljus inte var en longitudinell (som hade antagits) utan faktiskt en tvärgående våg . Den så kallade Huygens-Fresnel-principen var grunden för den fysiska optikens framsteg, och förklarade alla aspekter av ljusutbredning tills Maxwells elektromagnetiska teori kulminerade i utvecklingen av kvantmekaniken och upptäckten av fotonen .
Astronomi
Systema Saturnium
År 1655 upptäckte Huygens den första av Saturnus månar, Titan , och observerade och skissade Orionnebulosan med hjälp av ett brytande teleskop med en 43x förstoring av hans egen design. Huygens lyckades dela upp nebulosan i olika stjärnor (den ljusare insidan bär nu namnet Huygenian-regionen till hans ära), och upptäckte flera interstellära nebulosor och några dubbelstjärnor . Han var också den första som föreslog att Saturnus framträdande , som har förbryllat astronomer, berodde på "en tunn, platt ring, som inte rörde någonstans och lutade mot ekliptikan".
Mer än tre år senare, 1659, publicerade Huygens sin teori och fynd i Systema Saturnium . Det anses vara det viktigaste verket om teleskopisk astronomi sedan Galileos Sidereus Nuncius femtio år tidigare. Mycket mer än en rapport om Saturnus, gav Huygens mätningar för planeternas relativa avstånd från solen, introducerade konceptet mikrometer och visade en metod för att mäta vinkeldiametrar på planeter, vilket till slut gjorde det möjligt för teleskopet att användas som en instrument för att mäta (snarare än att bara observera) astronomiska objekt. Han var också den förste att ifrågasätta Galileos auktoritet i teleskopiska frågor, en känsla som skulle vara vanlig under åren efter dess publicering.
Samma år kunde Huygens observera Syrtis Major , en vulkanisk slätt på Mars . Han använde upprepade observationer av denna funktions rörelse under loppet av ett antal dagar för att uppskatta längden på dygnet på Mars, vilket han gjorde ganska exakt till 24 1/2 timme. Denna siffra är bara några minuter från den faktiska längden av Marsdagen på 24 timmar, 37 minuter.
Planetarium
På initiativ av Jean-Baptiste Colbert åtog sig Huygens uppgiften att bygga ett mekaniskt planetarium som kunde visa alla planeter och deras månar som då kändes cirkulerande runt solen. Huygens färdigställde sin design 1680 och lät bygga sin klockare Johannes van Ceulen året därpå. Emellertid gick Colbert bort under tiden och Huygens fick aldrig leverera sitt planetarium till den franska vetenskapsakademin eftersom den nya ministern, François-Michel le Tellier , beslutade att inte förnya Huygens kontrakt.
I sin design använde Huygens en genialisk användning av fortsatta fraktioner för att hitta de bästa rationella approximationerna genom vilka han kunde välja växlarna med rätt antal tänder. Förhållandet mellan två växlar bestämde omloppsperioderna för två planeter. För att flytta planeterna runt solen använde Huygens en klockmekanism som kunde gå framåt och bakåt i tiden. Huygens hävdade att hans planetarium var mer exakt än en liknande anordning konstruerad av Ole Rømer ungefär samtidigt, men hans planetariumsdesign publicerades inte förrän efter hans död i Opuscula Posthuma (1703).
Kosmoteorer
Strax före sin död 1695 avslutade Huygens sitt mest spekulativa arbete med titeln Cosmotheoros . På hans ledning skulle det endast publiceras postumt av hans bror, vilket Constantijn Jr gjorde 1698. I detta arbete spekulerade Huygens om existensen av utomjordiskt liv , som han föreställde sig liknande det på jorden. Sådana spekulationer var inte ovanliga på den tiden, motiverade av copernicanism eller plenitude-principen , men Huygens gick in mer i detalj. Men det gjorde det utan fördelen av att förstå Newtons gravitationslagar, eller det faktum att atmosfärerna på andra planeter är sammansatta av olika gaser. Cosmotheoros, översatt till engelska som The celestial worlds discover'd , har setts som en del av spekulativ fiktion i traditionen av Francis Godwin , John Wilkins och Cyrano de Bergerac . Huygens arbete var i grunden utopiskt och har en del inspiration från Peter Heylins kosmografi och planetariska spekulationer .
Huygens skrev att tillgången på vatten i flytande form var avgörande för liv och att vattnets egenskaper måste variera från planet till planet för att passa temperaturområdet. Han tog sina observationer av mörka och ljusa fläckar på Mars och Jupiters ytor som bevis på vatten och is på dessa planeter. Han hävdade att utomjordiskt liv varken bekräftas eller förnekas av Bibeln, och ifrågasatte varför Gud skulle skapa de andra planeterna om de inte skulle tjäna ett större syfte än att beundras från jorden. Huygens postulerade att det stora avståndet mellan planeterna betydde att Gud inte hade tänkt att varelser på en skulle få veta om varelserna på de andra, och att han inte hade förutsett hur mycket människor skulle gå framåt i vetenskaplig kunskap.
solsystemets relativa storlekar och sin metod för att beräkna stjärnavstånd . Han gjorde en serie mindre hål i en skärm vänd mot solen, tills han uppskattade ljuset var av samma intensitet som stjärnan Sirius . Han beräknade sedan att vinkeln på detta hål var 1/27 664 av solens diameter, och därmed var den cirka 30 000 gånger så långt bort, med det (felaktiga) antagandet att Sirius är lika lysande som solen. Ämnet för fotometri var i sin linda fram till Pierre Bouguers och Johann Heinrich Lamberts tid .
Arv
Under hans livstid var Huygens inflytande betydande men började blekna kort efter hans död. Hans färdigheter som geometer och hans mekaniska insikter väckte beundran hos många av hans samtida, inklusive Newton, Leibniz, l'Hôpital och Bernoullis . För sitt arbete inom fysik har Huygens ansetts vara en av de största vetenskapsmännen i 1600-talets Europa och en framstående figur i den vetenskapliga revolutionen, som bara konkurrerade med Newton i både djup insikt och antalet erhållna resultat. Huygens hjälpte också till att utveckla de institutionella ramarna för vetenskaplig forskning på den europeiska kontinenten , vilket gjorde honom till en ledande aktör i upprättandet av modern vetenskap.
Matematik och fysik

Inom matematiken behärskade Huygens metoderna för antik grekisk geometri , särskilt Arkimedes arbete, och var en skicklig användare av analytisk geometri och infinitesimala tekniker av Descartes, Fermat och andra. Hans matematiska stil kan karakteriseras som geometrisk infinitesimal analys av kurvor och av rörelse. Med inspiration och bildspråk från mekanik förblev det ren matematik i formen. Huygens avslutade denna typ av geometrisk analys, eftersom fler matematiker vände sig bort från klassisk geometri till kalkylen för att hantera oändliga små, gränsprocesser och rörelse.
Huygens kunde dessutom helt och hållet använda matematiken för att svara på frågor om fysik. Ofta innebar detta att man introducerade en enkel modell för att beskriva en komplicerad situation, sedan analyserade den med utgångspunkt från enkla argument till deras logiska konsekvenser, och utvecklade den nödvändiga matematiken längs vägen. Som han skrev i slutet av ett utkast till De vi Centrifuga :
Vad du än antar att det inte är omöjligt vare sig angående gravitation eller rörelse eller någon annan sak, om du sedan bevisar något angående storleken på en linje, yta eller kropp, så kommer det att vara sant; som till exempel Arkimedes på parabelns kvadratur , där tendensen hos tunga föremål har antagits verka genom parallella linjer.
Huygens gynnade axiomatiska presentationer av sina resultat, som kräver rigorösa metoder för geometrisk demonstration: även om han tillät nivåer av osäkerhet i valet av primära axiom och hypoteser, kunde bevisen för satser som härrör från dessa aldrig vara i tvivel. Huygens stil av publicering utövade ett inflytande i Newtons presentation av hans egna stora verk .
Förutom tillämpningen av matematik på fysik och fysik på matematik, förlitade Huygens sig på matematik som metod, särskilt dess förmåga att generera ny kunskap om världen. Till skillnad från Galileo, som använde matematiken främst som retorik eller syntes, använde Huygens konsekvent matematik som en metod för upptäckt och analys, och insisterade på att reduktionen av det fysiska till det geometriska tillfredsställer höga krav på passform mellan det verkliga och det ideala. Genom att kräva sådan matematisk dragbarhet och precision, satte Huygens ett exempel för artonhundratalets vetenskapsmän som Johann Bernoulli , Jean le Rond d'Alembert och Charles-Augustin de Coulomb .
Även om Huygens aldrig var avsedd för publicering använde han sig av algebraiska uttryck för att representera fysiska enheter i en handfull av sina manuskript om kollisioner. Detta skulle göra honom till en av de första som använde matematiska formler för att beskriva samband i fysiken, som det görs idag. Huygens kom också nära den moderna idén om gräns när han arbetade på sin Dioptrica, även om han aldrig använde begreppet utanför geometrisk optik.
Senare inflytande
Huygens ställning som den största vetenskapsmannen i Europa förmörkades av Newtons i slutet av 1600-talet, trots att, som Hugh Aldersey-Williams noterar, "Huygens prestation överträffar Newtons prestation i några viktiga avseenden". Hans mycket idiosynkratiska stil och ovilja att publicera sitt verk gjorde mycket för att minska hans inflytande i efterdyningarna av den vetenskapliga revolutionen, eftersom anhängare av Leibniz kalkyl och Newtons fysik tog centrala scenen.
Huygens analyser av kurvor som uppfyller vissa fysikaliska egenskaper, såsom cykloiden, ledde till senare studier av många andra sådana kurvor som kaustik, brachistochrone , segelkurva och kontaktledning. Hans tillämpning av matematik på fysik, såsom i hans studie av dubbelbrytning, skulle inspirera till nya utvecklingar inom matematisk fysik och rationell mekanik under de följande århundradena (om än på det nya språket i kalkylen). Dessutom utvecklade Huygens de oscillerande tidtagningsmekanismerna, pendeln och balansfjädern, som har använts sedan dess i mekaniska klockor och klockor . Dessa var de första pålitliga tidtagarna som var lämpliga för vetenskapligt bruk (t.ex. var det möjligt för första gången att göra exakta mätningar av soldagens ojämlikhet, vilket astronomer tidigare inte kunde göra). Hans arbete på detta område förutsåg föreningen av tillämpad matematik med maskinteknik under århundradena som följde.
Porträtt
Under sin livstid lät Huygens och hans far beställa ett antal porträtt. Dessa inkluderade:
- 1639 – Constantijn Huygens mitt bland sina fem barn av Adriaen Hanneman , målning med medaljonger, Mauritshuis , Haag
- 1671 – Porträtt av Caspar Netscher , Museum Boerhaave , Leiden, lån från Haags Historisch Museum
- c.1675 – Avbildning av Huygens i Établissement de l'Académie des Sciences et fondation de l'observatoire, 1666 av Henri Testelin . Colbert presenterar medlemmarna i den nygrundade Académie des Sciences för kung Ludvig XIV av Frankrike. Musée National du Château et des Trianons de Versailles , Versailles
- 1679 – Medaillon -porträtt i relief av den franske skulptören Jean-Jacques Clérion
- 1686 – Porträtt i pastell av Bernard Vaillant , Museum Hofwijck , Voorburg
- 1684 till 1687 – Gravyrer av G. Edelinck efter målningen av Caspar Netscher
- 1688 – Porträtt av Pierre Bourguignon (målare) , Royal Netherlands Academy of Arts and Sciences , Amsterdam
Åminnelse
European Space Agency som landade på Titan , Saturnus största måne, 2005 fick sitt namn efter honom.
Ett antal monument över Christiaan Huygens kan hittas över viktiga städer i Nederländerna, inklusive Rotterdam , Delft och Leiden .
Arbetar
Källa(r):
- 1650 – De Iis Quae Liquido Supernatant ( Om delar som flyter ovanför vätskor , opublicerad).
- 1651 – Theoremata de Quadratura Hyperboles, Ellipsis et Circuli , återpublicerad i Oeuvres Complètes , Tome XI.
- 1651 – Epistola, qua diluuntur ea quibus 'Εξέτασις [Exetasis] Cyclometriae Gregori à Sto. Vincentio impugnata fuit (tillägg).
- 1654 – De Circuli Magnitudine Inventa.
- 1654 – Illustrium Quorundam Problematum Constructiones (tillägg).
- 1655 – Horologium ( Klockan – kort pamflett om pendeluret).
- 1656 – De Saturni Luna Observatio Nova ( Om den nya observationen av Saturnus måne , som beskriver upptäckten av Titan ).
- 1656 – De Motu Corporum ex Percussione , publicerad postumt 1703.
- 1657 – De Ratiociniis in Ludo Aleae ( Van reeckening in spelen van geluck , översatt till latin av Frans van Schooten).
- 1659 – Systema Saturnium ( Saturnus system ).
- 1659 – De vi Centrifuga ( Angående centrifugalkraften ), publicerad postumt 1703.
- 1673 – Horologium Oscillatorium Sive de Motu Pendulorum ad Horologia Aptato Demonstrationes Geometricae (inkluderar hans teori om evolutioner och design av pendelklockor, tillägnad Ludvig XIV av Frankrike).
- 1684 – Astroscopia Compendiaria Tubi Optici Molimine Liberata ( sammansatta teleskop utan rör ).
- 1685 – Memoriën aengaende het slijpen van glasen tot verrekijckers (som handlar om slipning av linser).
- 1686 – Old Dutch : Kort onderwijs aengaende het gebruijck der horologiën tot het vinden der lenghten van Oost en West ( instruktioner om hur man använder klockor för att fastställa longituden till sjöss).
- 1690 – Traité de la Lumière (som handlar om ljusutbredningens natur).
- 1690 – Discours de la Cause de la Pesanteur ( Diskurs om gravitation , tillägg).
- 1691 – Lettre Touchant le Cycle Harmonique (kort traktat om 31-tonssystemet ).
- 1698 – Cosmotheoros (som handlar om solsystemet, kosmologi och utomjordiskt liv).
- 1703 – Opuscula Posthuma inklusive:
- De Motu Corporum ex Percussione ( Angående rörelser hos kolliderande kroppar, innehåller de första korrekta lagarna för kollision, från 1656).
- Descriptio Automati Planetarii (beskrivning och design av ett planetarium ).
- 1724 – Novus Cyclus Harmonicus (en avhandling om musik, publicerad i Leiden efter Huygens död).
- 1728 – Christiani Hugenii Zuilichemii, dum viveret Zelhemii Toparchae, Opuscula Posthuma ... (pub. 1728) Alternativ titel: Opera Reliqua , inklusive verk inom optik och fysik
- 1888–1950 – Huygens, Christiaan. Oeuvres complès. Kompletta verk, 22 volymer. Redaktörer D. Bierens de Haan (1–5), J. Bosscha (6–10), DJ Korteweg (11–15), AA Nijland (15), JA Vollgraf (16–22). Haag:
- Tome I: Korrespondens 1638–1656 (1888).
- Tome II: Korrespondens 1657–1659 (1889).
- Tome III: Korrespondens 1660–1661 (1890).
- Tome IV: Korrespondens 1662–1663 (1891).
- Tome V: Korrespondens 1664–1665 (1893).
- Tome VI: Korrespondens 1666–1669 (1895).
- Tome VII: Korrespondens 1670–1675 (1897).
- Tome VIII: Korrespondens 1676–1684 (1899).
- Tome IX: Korrespondens 1685–1690 (1901).
- Tome X: Korrespondens 1691–1695 (1905).
- Tome XI: Travaux mathématiques 1645–1651 (1908).
- Tome XII: Travaux mathématiques pures 1652–1656 (1910).
- Tome XIII, Fasc. I: Dioptrique 1653, 1666 (1916).
- Tome XIII, Fasc. II: Dioptrique 1685–1692 (1916).
- Tome XIV: Calcul des probabilités. Travaux de mathématiques pures 1655–1666 (1920).
- Tome XV: Observationer astronomiques. Système de Saturne. Travaux astronomiques 1658–1666 (1925).
- Tome XVI: Mécanique jusqu'à 1666. Slagverk. Question de l'existence et de la perceptibilité du mouvement absolu. Kraftcentrifug (1929).
- Tome XVII: L'horloge à pendule de 1651 à 1666. Travaux divers de physique, de mécanique et de technique de 1650 à 1666. Traité des couronnes et des parhélies (1662 ou 1663) (1932) .
- Tome XVIII: L'horloge à pendule ou à balancier de 1666 à 1695. Anecdota (1934).
- Tome XIX: Mécanique théorique et physique de 1666 à 1695. Huygens à l'Académie royale des sciences (1937).
- Tome XX: Musique et mathématique. Musique. Mathématiques de 1666 à 1695 (1940).
- Tome XXI: Cosmologie (1944).
- Tome XXII: Tillägg à la korrespondens. Varia. Biographie de Chr. Huygens. Catalog de la vente des livres de Chr. Huygens (1950).
Se även
- Förbränningsmotorns historia
- Lista över de största optiska teleskopen historiskt
- Fokker orgel
- Sekunder pendel
Vidare läsning
- Andriesse, CD (2005). Huygens: Mannen bakom principen . Förord av Sally Miedema. Cambridge University Press .
- Bell, AE (1947). Christian Huygens och vetenskapens utveckling under 1600-talet
- Boyer, CB (1968). A History of Mathematics , New York.
- Dijksterhuis, EJ (1961). Mekaniseringen av världsbilden: Pythagoras till Newton
- Hooijmaijers, H. (2005). Talande tid – Enheter för tidsmätning i Museum Boerhaave – A Descriptive Catalog , Leiden, Museum Boerhaave.
- Struik, DJ (1948). En kortfattad matematikens historia
- Van den Ende, H. et al. (2004). Huygens's Legacy, The golden age of the pendel clock , Fromanteel Ltd, Castle Town, Isle of Man.
- Yoder, J G. (2005). "Book on the pendel clock" i Ivor Grattan-Guinness , red., Landmark Writings in Western Mathematics . Elsevier: 33–45.
externa länkar
Primära källor, översättningar
-
Verk av Christiaan Huygens vid Project Gutenberg :
- C. Huygens (översatt av Silvanus P. Thompson, 1912), Treatise on Light ; Errata .
- Verk av eller om Christiaan Huygens på Internet Archive
-
Verk av Christiaan Huygens på LibriVox (public domain audiobooks)

- Clerke, Agnes Mary (1911). . Encyclopædia Britannica . Vol. 14 (11:e upplagan). s. 21–22.
- Korrespondens av Christiaan Huygens på Early Modern Letters Online
- De Ratiociniis i Ludo Aleae eller The Value of all Chances in Games of Fortune, 1657 Christiaan Huygens bok om sannolikhetsteori. En engelsk översättning publicerad 1714. Text pdf-fil.
- Horologium oscillatorium (tysk översättning, pub. 1913) eller Horologium oscillatorium (engelsk översättning av Ian Bruce) på pendelklockan
- ΚΟΣΜΟΘΕΩΡΟΣ ( Cosmotheoros ). (Engelsk översättning av latin, pub. 1698; undertiteln The celestial worlds discover'd: or, Conjectures angående invånare, växter och produktioner av världarna på planeterna. )
- C. Huygens (översatt av Silvanus P. Thompson), Traité de la lumière eller Treatise on light , London: Macmillan, 1912, archive.org/details/treatiseonlight031310mbp ; New York: Dover, 1962; Project Gutenberg, 2005, gutenberg.org/ebooks/14725 ; Errata
- Systema Saturnium 1659 text en digital upplaga av Smithsonian Libraries
- Om centrifugalkraften (1703)
- Huygens arbete på WorldCat
- Christiaan Huygens korrespondens i EMLO
- Christiaan Huygens biografi och prestationer
- Porträtt av Christiaan Huygens
- Huygens böcker, i digital faksimil från Linda Hall Library :
- (1659) Systema Saturnium (latin)
- (1684) Astroscopia compendiaria (latin)
- (1690) Traité de la lumiére (franska)
- (1698) ΚΟΣΜΟΘΕΩΡΟΣ, sive De terris cœlestibus (latin)
Museer
- Huygensmuseum Hofwijck i Voorburg, Nederländerna, där Huygens bodde och arbetade.
- Huygens Clocks- utställning från Science Museum, London
- Onlineutställning om Huygens i Leiden University Library (på holländska)
Övrig
- O'Connor, John J .; Robertson, Edmund F. , "Christiaan Huygens" , MacTutor History of Mathematics arkiv , University of St Andrews
- Huygens och musikteorin Huygens–Fokkers stiftelse — om Huygens 31 lika temperament och hur det har använts
- Christiaan Huygens på 1950-talets sedel på 25 holländska gulden.
- Christiaan Huygens vid Mathematics Genealogy Project
- Hur man uttalar "Huygens"
- 1629 födslar
- 1695 döda
- Nederländska uppfinnare från 1600-talet
- Nederländska matematiker från 1600-talet
- Nederländska filosofer från 1600-talet
- Holländska vetenskapsmän från 1600-talet
- Nederländska 1600-talsförfattare
- 1600-talets latinspråkiga författare
- Upplysningstiden
- Astronomi i Nederländska republiken
- Christiaan Huygens
- Upptäckare av månar
- holländska klockare
- Holländska medlemmar av den nederländska reformerade kyrkan
- Nederländska musikteoretiker
- holländska vetenskapliga instrumenttillverkare
- Geometrar
- Huygens familj
- Alumner från Leiden University
- Medlemmar av den franska vetenskapsakademin
- Optiska fysiker
- Originalstipendiater från Royal Society
- Forskare från Haag
- Teoretiska fysiker





















