Tidsutvidgning

Den här artikeln handlar om ett fysiskt koncept. För termen som används inom psykologi, se Tidsuppfattning .

Tidsdilatation förklarar varför två arbetsklockor kommer att rapportera olika tider efter olika accelerationer. Till exempel går tiden långsammare vid ISS och släpar efter ungefär 0,01 sekunder för var 12:e jordmånad som går. För att GPS- satelliter ska fungera måste de anpassa sig för liknande böjning av rumtiden för att korrekt koordinera med system på jorden.

Inom fysik och relativitetsteori är tidsdilatation skillnaden i förfluten tid mätt med två klockor . Det beror antingen på en relativ hastighet mellan dem ( särskild relativistisk "kinetisk" tidsdilatation) eller på en skillnad i gravitationspotential mellan deras platser ( allmän relativistisk gravitationstidsdilatation ). När ospecificerat, hänvisar "tidsutvidgning" vanligtvis till effekten på grund av hastighet.

Efter att ha kompenserat för varierande signalfördröjningar på grund av det ändrade avståndet mellan en observatör och en rörlig klocka (dvs. Dopplereffekt ), kommer observatören att mäta den rörliga klockan som tickande långsammare än en klocka som står i vila i observatörens egen referensram . Dessutom kommer en klocka som är nära en massiv kropp (och som därför har lägre gravitationspotential) att registrera mindre förfluten tid än en klocka som ligger längre från nämnda massiva kropp (och som har en högre gravitationspotential).

Dessa förutsägelser av relativitetsteorin har upprepade gånger bekräftats genom experiment, och de är av praktisk betydelse, till exempel i driften av satellitnavigeringssystem som GPS och Galileo . Tidsutvidgning har också varit föremål för science fiction-verk.

Historia

Huvudartikel: History of special relativity

Tidsutvidgning av Lorentz-faktorn förutspåddes av flera författare vid 1900-talets början. Joseph Larmor (1897), åtminstone för elektroner som kretsar kring en kärna, skrev "... individuella elektroner beskriver motsvarande delar av sina banor i tider kortare för [vila] systemet i förhållandet: 1 − v ${ \sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$ ". Emil Cohn (1904) relaterade specifikt denna formel till klockfrekvensen. Inom ramen för den speciella relativitetsteorien visade Albert Einstein (1905) att denna effekt gäller själva tidens natur, och han var också den förste att påpeka dess ömsesidighet eller symmetri. Därefter Hermann Minkowski (1907) begreppet riktig tid som ytterligare förtydligade innebörden av tidsutvidgning.

Tidsutvidgning orsakad av en relativ hastighet

Från den blå klockans lokala referensram uppfattas den röda klockan, när den är i rörelse, som att den tickar långsammare.

Särskild relativitet indikerar att, för en observatör i en tröghetsreferensram , kommer en klocka som rör sig i förhållande till dem att mätas så att den tickar långsammare än en klocka som är i vila i deras referensram. Detta fall kallas ibland för speciell relativistisk tidsutvidgning. Ju snabbare den relativa hastigheten är , desto större blir tidsutvidgningen mellan varandra, med tiden som saktar ner till stopp när man närmar sig ljusets hastighet (299 792 458 m/s).

Teoretiskt sett skulle tidsutvidgning göra det möjligt för passagerare i ett snabbt rörligt fordon att avancera längre in i framtiden på en kort tid av sin egen tid. För tillräckligt höga hastigheter är effekten dramatisk. Till exempel kan ett års resa motsvara tio år på jorden. Faktum är att en konstant acceleration på 1 g skulle tillåta människor att resa genom hela det kända universum under en mänsklig livstid.

Med nuvarande teknik som kraftigt begränsar rymdresornas hastighet är skillnaderna som upplevs i praktiken små: efter 6 månader på den internationella rymdstationen (ISS), som kretsar runt jorden med en hastighet av cirka 7 700 m/s, skulle en astronaut ha åldrats cirka 0,005 sekunder mindre än de på jorden. Kosmonauterna Sergei Krikalev och Sergei Avdeyev upplevde båda tidsdilatation på cirka 20 millisekunder jämfört med tiden som passerade på jorden.

Enkel slutledning

Vänster : Observatör i vila mäter tiden 2 L / c mellan samlokala händelser av ljussignalgenerering vid A och ankomst till A. Höger : Händelser enligt en observatör som rör sig till vänster om uppställningen: bottenspegel A när signal genereras kl. tid t'= 0, övre spegel B när signalen reflekteras vid tidpunkten t'=D/c , nedre spegel A när signalen återvänder vid tidpunkten t'=2D/c

Tidsdilatation kan härledas från den observerade konstansen av ljusets hastighet i alla referensramar som dikteras av det andra postulatet av speciell relativitet .

Denna konstanta ljushastighet gör att, mot intuitionen, är hastigheterna för materiella föremål och ljus inte additiv. Det är inte möjligt att få ljusets hastighet att verka högre genom att röra sig mot eller bort från ljuskällan.

Betrakta då en enkel vertikal klocka som består av två speglar A och B , mellan vilka en ljuspuls studsar. Separationen mellan speglarna är L och klockan tickar en gång varje gång ljuspulsen träffar spegel A .

I ramen där klockan står i vila (se vänster del av diagrammet), spårar ljuspulsen en väg med längden 2 L och klockans period är 2 L dividerat med ljusets hastighet:

$\Delta t={\frac {2L}{c}}$

Från referensramen för en rörlig observatör som färdas med hastigheten v i förhållande till klockans viloram (högra delen av diagrammet), ses ljuspulsen som en längre, vinklad bana. Att hålla ljusets hastighet konstant för alla tröghetsobservatörer kräver en förlängning av perioden för denna klocka ur den rörliga observatörens perspektiv. Det vill säga, mätt i en bildruta som rör sig i förhållande till den lokala klockan, kommer denna klocka att gå långsammare. Enkel tillämpning av Pythagoras sats leder till den välkända förutsägelsen av speciell relativitet:

Den totala tiden för ljuspulsen att spåra sin väg ges av:

$\Delta t'={\frac {2D}{c}}$

Längden på den halva banan kan beräknas som en funktion av kända kvantiteter som:

$D={\sqrt {\left({\frac {1}{2}}v\Delta t'\right)^{2}+L ^{2}}}$

Eliminering av variablerna D och L från dessa tre ekvationer resulterar i:

$\Delta t'={\frac {\Delta t}{\sqrt {1-{\frac {v^{2}}{c^{2} }}}}}$

som uttrycker det faktum att den rörliga observatörens period av klockan $\Delta t'$ är längre än perioden $\Delta t$ i själva klockans ram.

Eftersom alla klockor som har en gemensam period i den vilande ramen bör ha en gemensam period när de observeras från den rörliga ramen, bör alla andra klockor – mekaniska, elektroniska, optiska (som en identisk horisontell version av klockan i exemplet) – uppvisa samma hastighetsberoende tidsutvidgning.

Ömsesidighet

Tid UV för en klocka i S är kortare jämfört med Ux′ i S′, och tiden UV för en klocka i S′ är kortare jämfört med Ux i S

Transversal tidsdilatation. De blå prickarna representerar en ljuspuls. Varje par prickar med ljus "studsande" mellan dem är en klocka. I ramen för varje grupp av klockor mäts den andra gruppen för att ticka långsammare, eftersom den rörliga klockans ljuspuls måste färdas en längre sträcka än den stillastående klockans ljuspuls. Det är så, även om klockorna är identiska och deras relativa rörelse är perfekt ömsesidig.

Givet en viss referensram, och den "stationära" observatör som beskrivits tidigare, om en andra observatör följde med den "rörliga" klockan, skulle var och en av observatörerna uppfatta den andras klocka som att den tickar i en långsammare takt än sin egen lokala klocka , p.g.a. de uppfattar båda att den andra är den som är i rörelse relativt sin egen stationära referensram.

Sunt förnuft skulle diktera att, om tidens gång har saktat ner för ett rörligt föremål, skulle objektet observera att den yttre världens tid påskyndas i motsvarande grad. Motintuitivt förutspår speciell relativitetsteori motsatsen. När två observatörer är i rörelse i förhållande till varandra, kommer var och en att mäta den andras klocka som saktar ner, i enlighet med att de är i rörelse i förhållande till observatörens referensram.

Även om detta verkar motsägelsefullt, förekommer en liknande märklighet i vardagen. Om två personer A och B observerar varandra på avstånd, kommer B att framstå som liten för A, men samtidigt kommer A att verka liten för B. Att vara bekant med effekterna av perspektiv finns det ingen motsättning eller paradox i denna situation .

Fenomenets ömsesidighet leder också till den så kallade tvillingparadoxen där tvillingarnas åldrande, där den ena vistas på jorden och den andra ger sig ut på rymdresor, jämförs, och där ömsesidigheten antyder att båda personerna bör ha samma ålder när de återförena. Tvärtom, i slutet av rundresan kommer den resande tvillingen att vara yngre än syskonen på jorden. Dilemmat som paradoxen utgör kan dock förklaras av att den resande tvillingen måste accelerera markant i minst tre faser av resan (början, riktningsändringen och slutet), medan den andra endast kommer att uppleva försumbar acceleration, pga. till rotation och rotation av jorden. Under rymdfärdens accelerationsfaser är tidsutvidgningen inte symmetrisk.

Experimentell testning

Se även: Tester av speciell relativitet

Dopplereffekt

Huvudartikel: Ives–Stilwell-experiment

• Det uttalade syftet av Ives och Stilwell (1938, 1941) med dessa experiment var att verifiera tidsdilatationseffekten, förutspådd av Larmor-Lorentz eterteorin, på grund av rörelse genom etern med hjälp av Einsteins förslag att dopplereffekten i kanalstrålar skulle ge en lämplig experimentera. Dessa experiment mätte Doppler-förskjutningen av strålningen som sänds ut från katodstrålar , sett framifrån och direkt bakifrån. De upptäckta höga och låga frekvenserna var inte de klassiskt förutsagda värdena:
  $${\frac {f_{0}}{1-v/c}}\qquad {\text{and}}\qquad {\frac {f_{ 0}}{1+v/c}}$$
  De höga och låga frekvenserna av strålningen från de rörliga källorna mättes som:
  $${\sqrt { \frac {1+v/c}{1-v/c}}}f_{0}=\gamma \left(1+v/c\right)f_{0}\qquad {\text{and}}\ qquad {\sqrt {\frac {1-v/c}{1+v/c}}}f_{0}=\gamma \left(1-v/c\right)f_{0}\,$$
  som härleds av Einstein (1905) från Lorentz-transformationen , när källan går långsamt av Lorentz-faktorn.
• Hasselkamp, ​​Mondry och Scharmann (1979) mätte Dopplerskiftet från en källa som rörde sig i rät vinkel till siktlinjen. Det mest allmänna förhållandet mellan frekvenser av strålningen från de rörliga källorna ges av:
  $$f_{\mathrm {upptäckt} }=f_{\mathrm {rest } }{\left(1-{\frac {v}{c}}\cos \phi \right)/{\sqrt {1-{v^{2}}/{c^{2}}}}}$$
  enligt slutsatsen av Einstein (1905). För ϕ = 90° ( cos ϕ = 0 ) reduceras detta till f _detekterat = f _vila γ . Denna lägre frekvens från den rörliga källan kan tillskrivas tidsdilatationseffekten och kallas ofta för den tvärgående Dopplereffekten och förutspåddes av relativitetsteorin.
• 2010 observerades tidsutvidgning vid hastigheter på mindre än 10 meter per sekund med hjälp av optiska atomklockor sammankopplade med 75 meter optisk fiber.

Rörliga partiklar

Huvudartikel: Experimentell testning av tidsdilatation

• En jämförelse av myonlivslängder vid olika hastigheter är möjlig. I laboratoriet produceras långsamma myoner; och i atmosfären introduceras mycket snabbrörliga myoner av kosmiska strålar. Om man tar myonens livstid i vila som laboratorievärdet på 2,197 μs, är livslängden för en kosmisk strålningsproducerad myon som färdas med 98 % av ljusets hastighet ungefär fem gånger längre, i överensstämmelse med observationer. Ett exempel är Rossi och Hall (1941), som jämförde populationen av myoner som produceras av kosmisk strålning på toppen av ett berg med den som observerats vid havsnivån.
• Livslängden för partiklar som produceras i partikelacceleratorer är längre på grund av tidsdilatation. I sådana experiment är "klockan" den tid det tar för processer som leder till myons sönderfall, och dessa processer äger rum i den rörliga myonen med sin egen "klockhastighet", som är mycket långsammare än laboratorieklockan. Detta tas rutinmässigt med i beräkningen inom partikelfysik, och många dedikerade mätningar har utförts. Till exempel, i myonlagringsringen vid CERN visade sig livslängden för myoner som cirkulerade med γ = 29,327 vara dilaterade till 64,378 μs, vilket bekräftar tidsdilatation till en noggrannhet på 0,9 ± 0,4 promille.

Rätt tid och Minkowski-diagram

Minkowski-diagram och tvillingparadox

Klocka C i relativ rörelse mellan två synkroniserade klockor A och B. C möter A vid d och B vid f .

Tvillingparadox . En tvilling måste byta ram, vilket leder till olika rätta tider i tvillingens världslinjer.

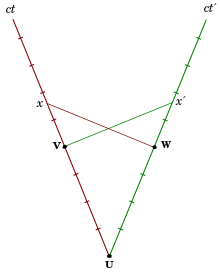
I Minkowski-diagrammet från den första bilden till höger möter klockan C som vilar i tröghetsramen S′ klockan A vid d och klockan B vid f (båda vilar i S). Alla tre klockorna börjar samtidigt ticka i S. A världslinjen är ct-axeln, världslinjen för B som skär f är parallell med ct-axeln och världslinjen för C är ct′-axeln. Alla händelser samtidigt med d i S är på x-axeln, i S′ på x′-axeln.

Den korrekta tiden mellan två händelser indikeras av en klocka som finns vid båda händelserna. Den är invariant, dvs i alla tröghetsramar är det överens om att denna tid indikeras av den klockan. Intervallet df är därför den korrekta tiden för klockan C och är kortare med avseende på koordinattiderna ef=dg för klockorna B och A i S. Omvänt är även korrekt tid ef för B kortare med avseende på tiden om i S. ′, eftersom händelse e mättes i S′ redan vid tidpunkten i på grund av relativitet av samtidighet, långt innan C började ticka.

Av det kan man se att den korrekta tiden mellan två händelser indikerad av en opaccelererad klocka närvarande vid båda händelserna, jämfört med den synkroniserade koordinattiden uppmätt i alla andra tröghetsramar, alltid är det minimala tidsintervallet mellan dessa händelser . Emellertid kan intervallet mellan två händelser också motsvara den korrekta tiden för accelererade klockor som finns vid båda händelserna. Under alla möjliga riktiga tider mellan två händelser är den rätta tiden för den opaccelererade klockan maximal , vilket är lösningen på tvillingparadoxen .

Härledning och formulering

Lorentzfaktor som funktion av hastighet (i naturliga enheter där c = 1). Observera att för små hastigheter (mindre än 0,1) är γ ungefär 1.

Förutom ljusklockan som används ovan kan formeln för tidsdilatation mer allmänt härledas från den tidsmässiga delen av Lorentz-transformationen . Låt det finnas två händelser där den rörliga klockan indikerar $t_{a}$ och ${\displaystyle t_{b}},$ alltså:

$t_{a}^{\prime }= {\frac {t_{a}-{\frac {vx_{a}}{c^{2}}}}{\sqrt {1-{\frac {v^{2}}{c^{2}} }}}},\ t_{b}^{\prime }={\frac {t_{b}-{\frac {vx_{b}}{c^{2}}}}{\sqrt {1-{ \frac {v^{2}}{c^{2}}}}}}$

Eftersom klockan förblir i vila i sin tröghetsram, följer den $x_{a}=x_{b}$ , alltså intervallet $\ Delta t^{\prime }=t_{b}^{\prime }-t_{a}^{\prime }$ ges av:

$\Delta t'=\gamma \,\Delta t={\frac {\Delta t}{\sqrt {1-{\frac { v^{2}}{c^{2}}}}}}\,$

där Δ t är tidsintervallet mellan två samlokala händelser (dvs. händer på samma plats) för en observatör i någon tröghetsram (t.ex. tickar på klockan), känd som den korrekta tiden , Δ t′ är tidsintervallet mellan samma händelser, mätta av en annan observatör, som rör sig trögt med hastigheten v med avseende på den tidigare observatören, v är den relativa hastigheten mellan observatören och den rörliga klockan, c är ljusets hastighet och Lorentz-faktorn (betecknas konventionellt med den grekiska bokstaven gamma eller γ) är:

$\gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}\,$

Sålunda visar sig varaktigheten av klockcykeln för en rörlig klocka vara ökad: den mäts vara "löpande långsam". Omfånget av sådana varianser i det vanliga livet, där v ≪ c , även med tanke på rymdresor, inte är tillräckligt stora för att producera lätt detekterbara tidsutvidgningseffekter och sådana försvinnande små effekter kan säkert ignoreras för de flesta ändamål. Det är först när ett föremål närmar sig hastigheter i storleksordningen 30 000 km/s (1/10 av ljusets hastighet) som tidsutvidgningen blir viktig.

Hyperbolisk rörelse

Huvudartikel: Hyperbolisk rörelse (relativitet)

I speciell relativitet beskrivs tidsdilatation enklast under omständigheter där den relativa hastigheten är oföränderlig. Icke desto mindre tillåter Lorentz-ekvationerna en att beräkna korrekt tid och rörelse i rymden för det enkla fallet med ett rymdskepp som appliceras med en kraft per massenhet, i förhållande till något referensobjekt i enhetlig (dvs konstant hastighet) rörelse, lika med g genomgående mätperioden.

₀ Låt t vara tiden i en tröghetsram som senare kallas vilobilden. Låt x vara en rumslig koordinat, och låt riktningen för den konstanta accelerationen samt rymdskeppets hastighet (relativt viloramen) vara parallella med x -axeln . Antag att rymdskeppets position vid tidpunkten t = 0 är x = 0 och hastigheten är v och definierar följande förkortning:

$\gamma _{0}={\frac {1}{\sqrt {1-v_{0}^{2}/c^{2}}}}$

följande formler gäller:

Placera:

$x(t)={\frac {c^{2}}{g}}\left({ \sqrt {1+{\frac {\left(gt+v_{0}\gamma _{0}\right)^{2}}{c^{2}}}}}-\gamma _{0}\ höger)$

Hastighet:

$v(t)={\frac {gt+v_{0}\gamma _{0}}{\sqrt {1+{\frac {\left(gt+v_{0}\gamma _{0}\right)^{2}}{c^{2}}}}}}$

Rätt tid som funktion av koordinattid:

$\tau (t)=\tau _{0}+\int _{0}^{t}{ \sqrt {1-\left({\frac {v(t')}{c}}\right)^{2}}}dt'$

₀₀ I fallet där v (0) = v = 0 och τ (0) = τ = 0 kan integralen uttryckas som en logaritmisk funktion eller, ekvivalent, som en invers hyperbolisk funktion :

$\tau (t)={\frac {c}{g }}\ln \left({\frac {gt}{c}}+{\sqrt {1+\left({\frac {gt}{c}}\right)^{2}}}\right)= {\frac {c}{g}}\operatörsnamn {arsinh} \left({\frac {gt}{c}}\right)$

Som funktioner av den rätta tiden $\tau$ för fartyget, gäller följande formler:

Placera:

$x(\tau )={\frac {c^{2}}{g}}\left(\cosh {\frac {g \tau }{c}}-1\höger)$

Hastighet:

$v(\tau )=c\tanh {\frac {g\tau }{c}}$

Koordinera tid som funktion av rätt tid:

$t(\tau )={\frac {c}{g}}\sinh {\frac {g\tau }{c}}$

Klockhypotes

Klockhypotesen är antagandet att hastigheten med vilken en klocka påverkas av tidsdilatation inte beror på dess acceleration utan bara på dess momentana hastighet. Detta motsvarar att säga att en klocka som rör sig längs en bana $P$ mäter rätt tid , definierad av:

$\tau =\int _{P}{\sqrt {dt^{2}- dx^{2}/c^{2}-dy^{2}/c^{2}-dz^{2}/c^{2}}}$

Klockhypotesen ingick implicit (men inte explicit) i Einsteins ursprungliga formulering från 1905 om speciell relativitet. Sedan dess har det blivit ett standardantagande och ingår vanligtvis i den speciella relativitetsteorien, särskilt i ljuset av experimentell verifiering upp till mycket höga accelerationer i partikelacceleratorer .

Tidsutvidgning orsakad av gravitation eller acceleration

Huvudartikel: Gravitationstidsdilatation

Tiden går snabbare längre från en tyngdpunkt, vilket man kan se med massiva föremål (som jorden)

Gravitationstidsdilatation upplevs av en observatör som vid en viss höjd inom en gravitationspotentialbrunn finner att deras lokala klockor mäter mindre förfluten tid än identiska klockor som ligger på högre höjd (och som därför har högre gravitationspotential).

Tyngdkraftsutvidgningen är på gång för t.ex. ISS-astronauter. Medan astronauternas relativa hastighet saktar ner deras tid, påskyndar den minskade gravitationspåverkan på deras plats den, om än i mindre grad. Dessutom går en klättrars tid teoretiskt något snabbare på toppen av ett berg jämfört med människor vid havsnivån. Det har också beräknats att på grund av tidsutvidgning jordens kärna 2,5 år yngre än jordskorpan . "En klocka som används för att tajma en hel rotation av jorden kommer att mäta dagen till att vara ungefär 10 extra ns/dag längre för varje km höjd över referensgeoiden." Resor till områden i rymden där extrem gravitationell tidsdilatation äger rum, såsom nära (men inte bortom händelsehorisonten för ) ett svart hål , kan ge tidsförskjutande resultat analogt med de för rymdresor i nära ljushastighet.

I motsats till hastighetstidsdilatation, där båda observatörerna mäter den andra som åldrande långsammare (en reciprok effekt), är gravitationstidsdilatation inte reciprok. Detta betyder att med gravitationstidsdilatation är båda observatörerna överens om att klockan närmare gravitationsfältets centrum är långsammare i takt, och de är överens om förhållandet mellan skillnaden.

Experimentell testning

Huvudartikel: Experimentell testning av tidsdilatation

• 1959 mätte Robert Pound och Glen A. Rebka den mycket lätta gravitationsrödförskjutningen i frekvensen av ljus som sänds ut på en lägre höjd, där jordens gravitationsfält är relativt intensivare. Resultaten låg inom 10 % av förutsägelserna av allmän relativitet. 1964 mätte Pound och JL Snider ett resultat inom 1% av det värde som förutspåtts av gravitationstidsdilatation. (Se Pound–Rebka-experiment )
• 2010 uppmättes gravitationstidsdilatation vid jordens yta med en höjdskillnad på endast en meter, med hjälp av optiska atomur.

Kombinerad effekt av hastighets- och gravitationstidsdilatation

Daglig tidsutvidgning (förstärkning eller förlust om negativ) i mikrosekunder som en funktion av (cirkulär) omloppsradie r = rs / re , där rs är satellitens omloppsradie och re är ekvatorjordens radie, beräknad med Schwarzschild-måttet. Vid r ≈ 1,497 finns ingen tidsutvidgning. Här upphäver effekterna av rörelse och minskad gravitation. ISS-astronauter flyger under, medan GPS och geostationära satelliter flyger ovanför.

Daglig tidsutvidgning över cirkulär omloppshöjd uppdelad i dess komponenter

Tidtagning med hög noggrannhet, satellitspårning i låg omloppsbana runt jorden och pulsartiming är tillämpningar som kräver övervägande av de kombinerade effekterna av massa och rörelse för att producera tidsdilatation. Praktiska exempel inkluderar International Atomic Time- standarden och dess förhållande till Barycentric Coordinate Time- standarden som används för interplanetära objekt.

Relativistiska tidsdilatationseffekter för solsystemet och jorden kan modelleras mycket exakt med Schwarzschilds lösning på Einsteins fältekvationer. I Schwarzschild- måttet ges intervallet ${\displaystyle dt_{\text{E}}} av:$

${ \displaystyle dt_{\text{E}}^{2}=\left(1-{\frac {2GM_{\text{i}}}{r_{\text{i}}c^{2}}}\ höger)dt_{\text{c}}^{2}-\left(1-{\frac {2GM_{\text{i}}}{r_{\text{i}}c^{2}}}\ höger)^{-1}{\frac {dx^{2}+dy^{2}+dz^{2}}{c^{2}}}}$

var:

• $dt_{\text{E}}$ är en liten ökning av korrekt tid $t_{\text{E}}$ (ett intervall som kan registreras på en atomur),
• $dt_{\text{c}}$ är ett litet steg i koordinaten $t_{\text{c}}$ ( koordinattid ),
• $dx,dy,dz$ är små steg i de tre koordinaterna $x,y,z$ för klockans position,
• ${\frac {-GM_{i}}{r_{i}}}$ representerar summan av de Newtonska gravitationspotentialerna på grund av massorna i grannskapet, baserat på deras avstånd ${ \displaystyle r_{i}}$ från klockan. Denna summa inkluderar eventuella tidvattenpotentialer.

Klockans koordinathastighet ges av:

$v^{2}={\frac {dx^{2}+dy^{2}+dz^{2}}{ dt_{\text{c}}^{2}}}$

Koordinattiden $t_{c}$ är tiden som skulle avläsas på en hypotetisk "koordinatklocka" belägen oändligt långt från alla gravitationsmassor ( ${\displaystyle U=0} )$ , och stationär i koordinatsystem ( $v=0$ ). Det exakta förhållandet mellan hastigheten för korrekt tid och hastigheten för koordinattiden för en klocka med en radiell hastighetskomponent är:

${\frac {dt_{\text{E}}}{dt_{\text{c}}}}={\sqrt {1+{\frac {2U}{c^ {2}}}-{\frac {v^{2}}{c^{2}}}+\left({\frac {c^{2}}{2U}}+1\höger)^{- 1}{\frac {{v_{\shortparallel }}^{2}}{c^{2}}}}}={\sqrt {1-\left(\beta ^{2}+\beta _{e }^{2}+{\frac {\beta _{\shortparallel }^{2}\beta _{e}^{2}}{1-\beta _{e}^{2}}}\right) }}$

var:

• $v_{\shortparallel }$ är den radiella hastigheten,
• $v_{e}={\sqrt {\frac {2GM_{i}}{r_{i}}}}$ är flykthastigheten,
• $\beta =v/c$ , $\beta _{e}=v_{e}/c$ och ${\ displaystyle \beta _{\shortparallel }=v_{\shortparallel }/c}$ är hastigheter i procent av ljusets hastighet c ,
• $U={\frac {-GM_{i}}{r_{i}}}$ är den newtonska potentialen; alltså $-U$ är lika med halva kvadraten på flykthastigheten.

Ovanstående ekvation är exakt under antagandena av Schwarzschild-lösningen. Den reducerar till hastighetstidsdilatationsekvationen i närvaro av rörelse och frånvaro av gravitation, dvs $\beta _{e}=0$ . Den reducerar till gravitationstidsdilatationsekvationen i frånvaro av rörelse och närvaro av gravitation, dvs $\beta =0=\beta _{\shortparallel }$ .

Experimentell testning

• Hafele och Keating , 1971, flög cesium atomklockor öster och väster runt jorden i kommersiella flygplan, för att jämföra den förflutna tiden med den för en klocka som fanns kvar vid US Naval Observatory . Två motsatta effekter spelade in. Klockorna förväntades åldras snabbare (visa en längre förfluten tid) än referensklockan eftersom de hade en högre (svagare) gravitationspotential under större delen av resan (jfr Pound–Rebka-experimentet ). Men också, som kontrast, förväntades de rörliga klockorna åldras långsammare på grund av hastigheten på deras färd. Från de faktiska flygvägarna för varje resa förutspådde teorin att de flygande klockorna, jämfört med referensklockorna vid US Naval Observatory, borde ha tappat 40±23 nanosekunder under resan österut och borde ha ökat 275±21 nanosekunder under resan västerut. . I förhållande till den atomära tidsskalan för US Naval Observatory förlorade de flygande klockorna 59±10 nanosekunder under resan österut och fick 273±7 nanosekunder under resan västerut (där felstaplarna representerar standardavvikelse). År 2005 National Physical Laboratory i Storbritannien sin begränsade replikering av detta experiment. NPL-experimentet skilde sig från originalet genom att cesiumklockorna skickades på en kortare resa (London–Washington, DC retur), men klockorna var mer exakta. De rapporterade resultaten ligger inom 4 % av relativitetsförutsägelserna, inom mätningarnas osäkerhet.
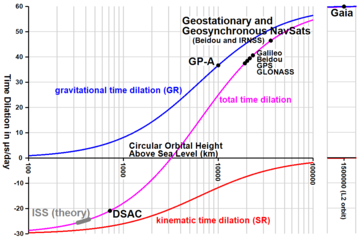
• Global Positioning System kan betraktas som ett kontinuerligt fungerande experiment i både speciell och allmän relativitetsteori. Klockorna i omloppsbana korrigeras för både speciella och allmänna relativistiska tidsutvidgningseffekter enligt beskrivningen ovan , så att de (som observerats från jordens yta) går i samma takt som klockor på jordens yta.

I populärkulturen

Hastighet och gravitationstidsdilatation har varit föremål för science fiction-verk i en mängd olika medier. Några exempel inom film är filmerna Interstellar och Planet of the Apes . I Interstellar involverar en viktig plotpunkt en planet, som är nära ett roterande svart hål och på vars yta en timme motsvarar sju år på jorden på grund av tidsutvidgning. Fysikern Kip Thorne samarbetade för att göra filmen och förklarade dess vetenskapliga begrepp i boken The Science of Interstellar .

Tidsdilatation användes i Doctor Who -avsnitten World Enough och Time och The Doctor Falls , som utspelar sig på ett rymdskepp i närheten av ett svart hål. På grund av det svarta hålets enorma gravitationskraft och fartygets längd (400 miles) går tiden snabbare i ena änden än den andra. När Doktorns följeslagare, Bill, blir förd till andra änden av skeppet, väntar hon i flera år på att han ska rädda henne; på hans tid går det bara minuter. Dessutom tillåter utvidgningen att Cybermen kan utvecklas i en "snabbare" takt än vad som tidigare setts i showen.

Tau Zero , en roman av Poul Anderson , är ett tidigt exempel på begreppet inom science fiction-litteratur. I romanen använder en rymdfarkost en Bussard ramjet för att accelerera till tillräckligt höga hastigheter för att besättningen tillbringar fem år ombord, men det går trettiotre år på jorden innan de når sin destination. Hastighetens tidsdilatation förklaras av Anderson i termer av tau-faktorn som minskar närmare och närmare noll när skeppet närmar sig ljusets hastighet - därav titeln på romanen. På grund av en olycka kan besättningen inte stoppa accelerationen av rymdfarkosten, vilket orsakar en sådan extrem tidsutvidgning att besättningen upplever Big Crunch i slutet av universum. Andra exempel i litteraturen, som Rocannons värld och The Forever War , använder sig på liknande sätt av relativistisk tidsutvidgning som en vetenskapligt rimlig litterär anordning för att få vissa karaktärer att åldras långsammare än resten av universum.

Se även

• Längdsammandragning
• Mässa i speciell relativitetsteori

Vidare läsning

•   Callender, C. ; Edney, R. (2001). Introduktion av tid . Ikon böcker . ISBN 978-1-84046-592-1 .
• Einstein, A. (1905). "Zur Elektrodynamik bewegter Körper" . Annalen der Physik . 322 (10): 891. Bibcode : 1905AnP...322..891E . doi : 10.1002/andp.19053221004 .
• Einstein, A. (1907). "Über die Möglichkeit einer neuen Prüfung des Relativitätsprinzips" . Annalen der Physik . 328 (6): 197–198. Bibcode : 1907AnP...328..197E . doi : 10.1002/andp.19073280613 .
•   Hasselkamp, ​​D.; Mondry, E.; Scharmann, A. (1979). "Direkt observation av den tvärgående Doppler-Skiften". Zeitschrift für Physik A . 289 (2): 151–155. Bibcode : 1979ZPhyA.289..151H . doi : 10.1007/BF01435932 . S2CID 120963034 .
• Ives, HE; Stilwell, GR (1938). "En experimentell studie av hastigheten på en rörlig klocka". Journal of the Optical Society of America . 28 (7): 215–226. Bibcode : 1938JOSA...28..215I . doi : 10.1364/JOSA.28.000215 .
• Ives, HE; Stilwell, GR (1941). "En experimentell studie av hastigheten på en rörlig klocka. II". Journal of the Optical Society of America . 31 (5): 369–374. Bibcode : 1941JOSA...31..369I . doi : 10.1364/JOSA.31.000369 .
• Joos, G. (1959). "Bewegte Bezugssysteme in der Akustik. Der Doppler-Effekt". Lehrbuch der Theoretischen Physik, Zweites Buch (11:e upplagan).
• Larmor, J. (1897). "Om en dynamisk teori om det elektriska och lysande mediet" . Philosophical Transactions of the Royal Society . 190 : 205–300. Bibcode : 1897RSPTA.190..205L . doi : 10.1098/rsta.1897.0020 . (tredje och sista i en serie tidningar med samma namn).
• Poincaré, H. (1900). "La théorie de Lorentz et le principe de Réaction". Arkiv Néerlandaises . 5 : 253-78.
•   Puri, A. (2015). "Einstein kontra den enkla pendelformeln: saktar gravitationen ned alla klockor?". Fysisk utbildning . 50 (4): 431. Bibcode : 2015PhyEd..50..431P . doi : 10.1088/0031-9120/50/4/431 . S2CID 118217730 .
• Reinhardt, S.; et al. (2007). "Test av relativistisk tidsdilatation med snabba optiska atomklockor vid olika hastigheter" ( PDF) . Naturfysik . 3 (12): 861–864. Bibcode : 2007NatPh...3..861R . doi : 10.1038/nphys778 . Arkiverad från originalet (PDF) 2009-07-12.
• Rossi, B.; Hall, DB (1941). "Variation av sönderfallshastigheten för mesotroner med momentum". Fysisk granskning . 59 (3): 223. Bibcode : 1941PhRv...59..223R . doi : 10.1103/PhysRev.59.223 .
• Weiss, M. "Two way time transfer for satellites" . National Institute of Standards and Technology . Arkiverad från originalet 2017-05-29.
• Voigt, W. (1887). "Über das Doppler'sche princip". Nachrichten von der Königlicher Gesellschaft der Wissenschaften zu Göttingen . 2 : 41–51.

externa länkar

• Merrifield, Michael. "Lorentz-faktor (och tidsutvidgning)" . Sextio symboler . Brady Haran för University of Nottingham .