Jerk (fysik)

Ryck
Tidsderivat av position, inklusive ryck
Vanliga symboler	j , j , ȷ →
I SI-basenheter	m / s 3
Dimensionera	L T −3

₀ Inom fysiken är ryck eller ryck den hastighet med vilken ett objekts acceleration ändras i förhållande till tiden. Det är en vektorkvantitet (som har både storlek och riktning). Ryck betecknas oftast med symbolen j och uttrycks i m/s ³ ( SI-enheter ) eller standardvikt per sekund ( g /s).

Uttryck

Som en vektor kan ryck j uttryckas som första tidsderivata av acceleration , andra tidsderivata av hastighet och tredje tidsderivata av position :

$$\mathbf {j} (t)={\frac {\mathrm {d} \mathbf {a} (t)}{\mathrm {d} t}}={\frac {\mathrm {d} ^{2}\mathbf {v} (t)}{\mathrm {d} t^{2}}}={\frac {\mathrm {d} ^{3}\mathbf {r} (t)}{\mathrm {d} t^{3}}}$$

Var:

• a är acceleration
• v är hastighet
• r är position
• det är tid

differentialekvationer av tredje ordningen

$$J\left({\overset {\mathbf {...} }{x}},{\ddot {x}},{\ punkt {x}},x\right)=0$$

kallas ibland jerk-ekvationer . När de konverteras till ett ekvivalent system av tre vanliga icke-linjära differentialekvationer av första ordningen , är jerk-ekvationer den minimala inställningen för lösningar som visar kaotiskt beteende . Detta tillstånd genererar matematiskt intresse för rycksystem . System som involverar fjärde ordningens derivator eller högre kallas följaktligen hyperjerk-system .

Fysiologiska effekter och mänsklig perception

Se även: Mänsklig tolerans för g-kraft och hur mänsklig fysiologi bearbetar och reagerar på rörelse

Människokroppens position kontrolleras genom att balansera krafterna från antagonistiska muskler . Vid balansering av en given kraft, såsom att hålla upp en vikt, upprättar den postcentrala gyrusen en kontrollslinga för att uppnå den önskade jämvikten . Om kraften ändras för snabbt kan musklerna inte slappna av eller spänna sig tillräckligt snabbt och skjuta över i endera riktningen, vilket orsakar en tillfällig förlust av kontroll. Reaktionstiden för att reagera på förändringar i kraft beror på fysiologiska begränsningar och hjärnans uppmärksamhetsnivå : en förväntad förändring kommer att stabiliseras snabbare än en plötslig minskning eller ökning av belastningen.

För att undvika att fordonspassagerare tappar kontrollen över kroppens rörelser och skadas är det nödvändigt att begränsa exponeringen för både maximal kraft (acceleration) och maximalt ryck, eftersom det krävs tid för att justera muskelspänningen och anpassa sig till även begränsade stressförändringar. Plötsliga förändringar i accelerationen kan orsaka skador som whiplash . Överdrivet ryck kan också resultera i en obekväm åktur, även på nivåer som inte orsakar skada. Ingenjörer lägger ner avsevärd designansträngning för att minimera "ryckiga rörelser" på hissar , spårvagnar och andra transportmedel.

Tänk till exempel på effekterna av acceleration och ryck när du åker i en bil:

• Skickliga och erfarna förare kan accelerera smidigt, men nybörjare ger ofta en ryckig åktur. Vid växling i en bil med fotmanövrerad koppling begränsas accelerationskraften av motorkraften, men en oerfaren förare kan orsaka kraftiga ryck på grund av intermittent kraftstängning över kopplingen.
• Känslan av att pressas ner i sätena i en kraftfull sportbil beror på accelerationen. När bilen startar från vila sker ett stort positivt ryck då accelerationen snabbt ökar. Efter lanseringen sker ett litet, ihållande negativt ryck när kraften i luftmotståndet ökar med bilens hastighet, vilket gradvis minskar accelerationen och minskar kraften som pressar passageraren in i sätet. När bilen når sin toppfart har accelerationen nått 0 och förblir konstant, varefter det inte sker något ryck förrän föraren bromsar in eller ändrar riktning.
• Vid plötslig inbromsning eller vid kollisioner piskar passagerarna framåt med en initial acceleration som är större än under resten av inbromsningsprocessen eftersom muskelspänningar snabbt återtar kontrollen över kroppen efter inbromsningen eller kollisionen. Dessa effekter modelleras inte i fordonstestning eftersom kadaver och krocktestdockor inte har aktiv muskelkontroll.
• För att minimera effekterna av ett ryck är kurvor längs vägar utformade för att vara klotoider , liksom järnvägskurvor och berg-och dalbana .

Kraft, acceleration och ryck

För en konstant massa m är accelerationen a direkt proportionell mot kraften F enligt Newtons andra rörelselag :

$$\mathbf {F} =m\mathbf {a}$$

I klassisk mekanik av stela kroppar finns inga krafter associerade med derivator av acceleration; fysiska system upplever dock svängningar och deformationer som ett resultat av ryck. Vid utformningen av rymdteleskopet Hubble satte NASA gränser för både ryck och hopp .

Abraham -Lorentz-kraften är rekylkraften på en accelererande laddad partikel som avger strålning. Denna kraft är proportionell mot partikelns ryck och mot kvadraten på dess laddning . Wheeler -Feynman-absorberteorin är en mer avancerad teori, tillämplig i en relativistisk och kvantomgivning, och som tar hänsyn till självenergi .

I en idealiserad miljö

Diskontinuiteter i acceleration förekommer inte i verkliga miljöer på grund av deformation , kvantmekaniska effekter och andra orsaker. En hopp-diskontinuitet i accelerationen och följaktligen ett obegränsat ryck är dock möjliga i en idealiserad miljö, såsom en idealiserad punktmassa som rör sig längs en bitvis jämn , hel kontinuerlig bana. Hopp-diskontinuiteten uppstår vid punkter där banan inte är jämn. Extrapolerat från dessa idealiserade inställningar kan man kvalitativt beskriva, förklara och förutsäga effekterna av ryck i verkliga situationer.

Hopp-diskontinuitet i acceleration kan modelleras med hjälp av en Dirac deltafunktion i ryck, skalad till hoppets höjd. Att integrera ryck över tid över Dirac-deltat ger hopp-diskontinuiteten.

Betrakta till exempel en bana längs en båge med radien r , som tangentiellt ansluter till en rät linje. Hela vägen är kontinuerlig, och dess delar är jämna. Antag nu att en punktpartikel rör sig med konstant hastighet längs denna väg, så dess tangentiella acceleration är noll. Centripetalaccelerationen som ges av v ² / r är vinkelrät mot bågen och inåt . När partikeln passerar kopplingen av bitar, upplever den en hopp-diskontinuitet i accelerationen given av v ² / r , och den genomgår ett ryck som kan modelleras av ett Dirac-delta, skalat till hopp-diskontinuiteten.

För ett mer påtagligt exempel på diskontinuerlig acceleration, överväg ett idealiskt fjäder-massasystem med massan som oscillerar på en idealiserad yta med friktion. Kraften på massan är lika med vektorsumman av fjäderkraften och den kinetiska friktionskraften . När hastigheten ändrar tecken (vid maximala och minimala förskjutningar ), ändras storleken på kraften på massan med två gånger storleken på friktionskraften, eftersom fjäderkraften är kontinuerlig och friktionskraften ändrar riktning med hastigheten. Hoppet i acceleration är lika med kraften på massan dividerat med massan. Det vill säga, varje gång massan passerar genom en minimal eller maximal förskjutning, upplever massan en diskontinuerlig acceleration, och rycket innehåller ett Dirac-delta tills massan stannar. Den statiska friktionskraften anpassar sig till den kvarvarande fjäderkraften och skapar jämvikt med noll nettokraft och noll hastighet.

Tänk på exemplet med en bromsande och bromsande bil. Bromsbeläggen genererar kinetiska friktionskrafter och konstanta bromsmoment på skivorna ( eller trummorna ) ) av hjulen. Rotationshastigheten minskar linjärt till noll med konstant vinkelretardation. Friktionskraften, vridmomentet och bilens retardation når plötsligt noll, vilket indikerar ett Dirac-delta i fysiskt ryck. Dirac-deltat jämnas ut av den verkliga miljön, vars kumulativa effekter är analoga med dämpning av det fysiologiskt upplevda rycket. Det här exemplet försummar effekterna av däckglidning, fjädringsdoppning, verklig avböjning av alla idealiskt stela mekanismer, etc.

Ett annat exempel på betydande ryck, analogt med det första exemplet, är skärningen av ett rep med en partikel på änden. Antag att partikeln oscillerar i en cirkulär bana med en centripetalacceleration som inte är noll. När repet kapas ändras partikelns bana abrupt till en rak bana, och kraften i riktningen inåt ändras plötsligt till noll. Föreställ dig en monomolekylär fiber skuren av en laser; partikeln skulle uppleva mycket höga ryck på grund av den extremt korta skärtiden.

I rotation

Geneva-enhet i fyra lägen i drift

Tidsdiagram över ett varv för vinkel, vinkelhastighet, vinkelacceleration och vinkelryck

Betrakta en stel kropp som roterar runt en fast axel i en tröghetsreferensram . Om dess vinkelposition som funktion av tiden är θ ( t ) , kan vinkelhastigheten, accelerationen och rycket uttryckas på följande sätt:

• Vinkelhastighet , $\omega (t)={\dot {\theta }}(t)={\frac {\mathrm {d } \theta (t)}{\mathrm {d} t}}$ , är tidsderivatan av θ ( t ) .
• Vinkelacceleration , $\alpha (t)={\dot {\omega }}(t)={\frac {\mathrm {d } \omega (t)}{\mathrm {d} t}}$ , är tidsderivatan av ω ( t ) .
• Vinkelryck, $\zeta (t)={\dot {\alpha }}(t)={\ddot {\omega }}(t)={\overset {...}{\theta }}( t)$ , är tidsderivatan av α ( t ) .

Vinkelacceleration är lika med vridmomentet som verkar på kroppen, dividerat med kroppens tröghetsmoment med avseende på den momentana rotationsaxeln. En förändring av vridmomentet resulterar i vinkelryck.

Det allmänna fallet med en roterande stel kropp kan modelleras med hjälp av kinematisk skruvteori , som inkluderar en axiell vektor , vinkelhastighet Ω ( t ) och en polär vektor , linjär hastighet v ( t ) . Från detta definieras vinkelaccelerationen som

$${\boldsymbol {\alpha }}(t)={\frac {\mathrm {d} }{\mathrm {d} t }}{\boldsymbol {\Omega }}(t)={\dot {\boldsymbol {\Omega }}}(t)$$

och det kantiga rycket ges av

$${\boldsymbol {\zeta }}(t)={\frac {\mathrm {d} }{ \mathrm {d} t}}{\boldsymbol {\alpha }}(t)={\dot {\boldsymbol {\alpha }}}(t)={\ddot {\boldsymbol {\Omega }}}(t )$$

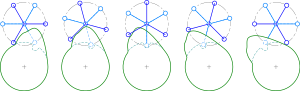
Tänk till exempel på en Genève-enhet , en enhet som används för att skapa intermittent rotation av ett driven hjul (det blå hjulet i animationen) genom kontinuerlig rotation av ett drivande hjul (det röda hjulet i animationen). Under en cykel av drivhjulet ändras det drivna hjulets vinkelposition θ med 90 grader och förblir sedan konstant. På grund av den ändliga tjockleken på drivhjulets gaffel (springan för drivstiftet) genererar denna anordning en diskontinuitet i vinkelaccelerationen α och ett obegränsat vinkelryck ζ i det drivna hjulet.

Jerk utesluter inte att Genève-enheten används i applikationer som filmprojektorer och kameror. I filmprojektorer går filmen fram bildruta för bildruta, men projektordriften har lågt brus och är mycket tillförlitlig på grund av den låga filmbelastningen (endast en liten del av filmen som väger några gram drivs), den måttliga hastigheten (2,4) m/s), och den låga friktionen.

Dubbla kamdrifter

_ 1/6 per varv

_ 1/3 per varv

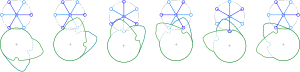
Med kamdrivsystem kan användning av en dubbel kam undvika rycket från en enda kam; dock är den dubbla kammen skrymmande och dyrare. Dual-cam-systemet har två kammar på en axel som växlar en andra axel med en bråkdel av ett varv. Grafiken visar stegdrivningar med en sjättedels och en tredjedels rotation per varv på drivaxeln. Det finns inget radiellt spel eftersom två armar på det stegade hjulet alltid är i kontakt med dubbelkammen. Generellt kan kombinerade kontakter användas för att undvika ryck (och slitage och buller) som är förknippade med en enskild följeslagare (såsom en enda följeslagare som glider längs en slits och ändrar dess kontaktpunkt från ena sidan av slitsen till den andra kan undvikas genom att med två följare som glider längs samma spår, en sida vardera).

I elastiskt deformerbart material

Kompressionsvågmönster

Plan våg

Cylindrisk symmetri

En elastiskt deformerbar massa deformeras under en applicerad kraft (eller acceleration); deformationen är en funktion av dess styvhet och kraftens storlek . Om förändringen i kraft är långsam är rycket litet, och utbredningen av deformation anses vara momentan jämfört med förändringen i acceleration. Den förvrängda kroppen agerar som om den var i en kvasistatisk regim , och endast en föränderlig kraft (icke noll ryck) kan orsaka utbredning av mekaniska vågor (eller elektromagnetiska vågor) för en laddad partikel); därför bör en stötvåg och dess fortplantning genom kroppen övervägas för icke-noll till högt ryck.

Utbredningen av deformation visas i grafiken "Kompressionsvågmönster" som en kompressionsplan våg genom ett elastiskt deformerbart material. För vinkelryck visas också deformationsvågorna som utbreder sig i ett cirkulärt mönster, vilket orsakar skjuvspänning och möjligen andra vibrationssätt . Reflexionen av vågor längs gränserna orsakar konstruktiva interferensmönster (ej avbildade), vilket ger spänningar som kan överskrida materialets gränser. Deformationsvågorna kan orsaka vibrationer, vilket kan leda till buller, slitage och fel, särskilt i fall av resonans.

Stång med massiv topp

Den grafiska rubriken "Stång med massiv topp" visar ett block kopplat till en elastisk stång och en massiv topp. Stången böjer sig när blocket accelererar, och när accelerationen upphör, kommer toppen att svänga ( dämpad ) under regimen av stavstyvhet. Man skulle kunna hävda att ett större (periodiskt) ryck kan excitera en större oscillationsamplitud eftersom små svängningar dämpas innan förstärkning av en stötvåg. Man kan också hävda att ett större ryck kan öka sannolikheten för att excitera ett resonansläge eftersom de större vågkomponenterna i stötvågen har högre frekvenser och Fourierkoefficienter .

Sinusformad accelerationsprofil

För att minska amplituden av exciterade stressvågor och vibrationer kan man begränsa ryck genom att forma rörelse och göra accelerationen kontinuerlig med sluttningar så plana som möjligt. På grund av abstrakta modellers begränsningar inkluderar algoritmer för att reducera vibrationer högre derivator, till exempel hopp , eller föreslår kontinuerliga regimer för både acceleration och ryck. Ett koncept för att begränsa ryck är att forma acceleration och retardation sinusformigt med noll acceleration däremellan (se grafisk rubrik "Sinusformad accelerationsprofil"), vilket gör att hastigheten ser sinusformad ut med konstant maxhastighet. Rycket kommer dock att förbli diskontinuerligt vid de punkter där accelerationen går in i och lämnar nollfaserna.

I geometrisk utformning av vägar och spår

En spårövergångskurva begränsar ryck. Övergången visas i rött mellan den blå räta linjen och den gröna bågen.

Vägar och spår är utformade för att begränsa rycket som orsakas av förändringar i deras kurvatur. På järnväg använder designers 0,35 m/s ³ som designmål och 0,5 m/s ³ som max. Spårövergångskurvor begränsar rycket vid övergång från en rak linje till en kurva, eller vice versa. Kom ihåg att i konstant hastighetsrörelse längs en båge är ryck noll i tangentiell riktning och icke-noll i inåtriktad normalriktning. Övergångskurvor ökar gradvis krökningen och, följaktligen, centripetalaccelerationen.

En Euler-spiral , den teoretiskt optimala övergångskurvan, ökar linjärt centripetalaccelerationen och resulterar i konstant ryck (se grafik). I verkliga tillämpningar är banans plan lutande ( cant ) längs de krökta sektionerna. Lutningen orsakar vertikal acceleration, vilket är en designhänsyn för slitage på banan och banvallen. Wiener Kurve (Wiener Curve) är en patenterad kurva designad för att minimera detta slitage.

Berg-och dalbanor är också designade med spårövergångar för att begränsa ryck. När du går in i en slinga kan accelerationsvärdena nå cirka 4 g (40 m/s ² ), och att åka i denna miljö med hög acceleration är endast möjligt med spårövergångar. S-formade kurvor, som till exempel åttor, använder också spårövergångar för mjuka turer.

I rörelsekontroll

I rörelsekontroll ligger designfokus på rak, linjär rörelse, med behovet av att flytta ett system från en stadig position till en annan (punkt-till-punkt-rörelse). Designfrågan ur ett ryckperspektiv är vertikalt ryck; rycket från tangentiell acceleration är faktiskt noll eftersom linjär rörelse är icke-roterande.

Tillämpningar för rörelsekontroll inkluderar passagerarhissar och bearbetningsverktyg. Att begränsa vertikala ryck anses vara avgörande för bekvämligheten att åka hiss. ISO 18738 specificerar mätmetoder för hisskörningskvalitet med avseende på ryck, acceleration, vibrationer och buller; standarden anger dock nivåer för acceptabel eller oacceptabel åkkvalitet. Det rapporteras att de flesta passagerare bedömer ett vertikalt ryck på 2 m/s ³ som acceptabelt och 6 m/s ³ som oacceptabelt. För sjukhus är 0,7 m/s ³ den rekommenderade gränsen.

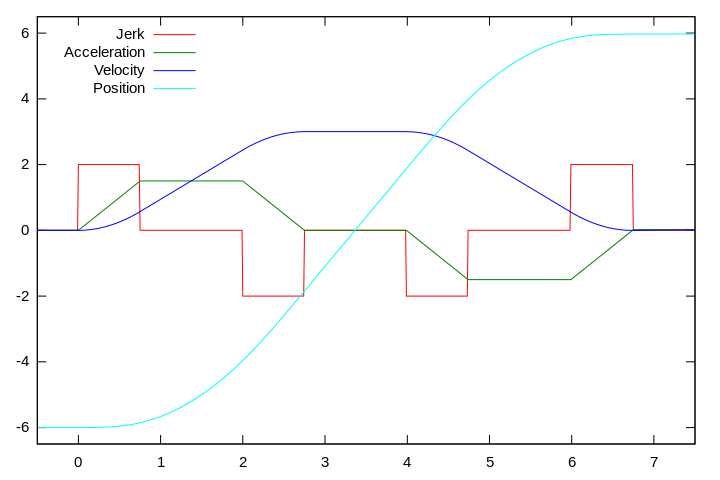
Ett primärt designmål för rörelsekontroll är att minimera övergångstiden utan att överskrida hastighets-, accelerations- eller ryckgränser. Betrakta en tredje ordningens rörelsekontrollprofil med kvadratiska rampnings- och derampningsfaser i hastighet (se figur).

Denna rörelseprofil består av följande sju segment:

1. Accelerationsuppbyggnad — positiv ryckgräns; linjär ökning av accelerationen till den positiva accelerationsgränsen; kvadratisk ökning av hastigheten
2. Övre accelerationsgräns — noll ryck; linjär hastighetsökning
3. Accelerationsramp nedåt — negativt ryckgräns; linjär minskning av accelerationen; (negativ) kvadratisk ökning av hastigheten, närmar sig den önskade hastighetsgränsen
4. Hastighetsgräns — noll ryck; noll acceleration
5. Uppbyggnad av retardation — negativ ryckgräns; linjär minskning av accelerationen till den negativa accelerationsgränsen; (negativ) kvadratisk minskning av hastigheten
6. Nedre retardationsgräns — noll ryck; linjär minskning av hastigheten
7. Retardationsramp ner — positiv ryckgräns; linjär ökning av accelerationen till noll; kvadratisk minskning av hastighet; närmar sig önskat läge med nollhastighet och nollacceleration

Segment fyras tidsperiod (konstant hastighet) varierar med avståndet mellan de två positionerna. Om detta avstånd är så litet att det inte skulle räcka att utelämna segment fyra, skulle segment två och sex (konstant acceleration) kunna reduceras lika mycket, och gränsen för konstant hastighet skulle inte nås. Om denna modifiering inte tillräckligt minskar det korsade avståndet, skulle segment ett, tre, fem och sju kunna förkortas lika mycket, och de konstanta accelerationsgränserna skulle inte nås.

Andra rörelseprofilstrategier används, såsom att minimera ryckkvadraten för en given övergångstid och, som diskuterats ovan, sinusformade accelerationsprofiler. Rörelseprofiler är skräddarsydda för specifika applikationer inklusive maskiner, personbilar, kättingtelfer, bilar och robotar.

I tillverkningen

Jerk är en viktig faktor i tillverkningsprocesser . Snabba förändringar i accelerationen av ett skärverktyg kan leda till för tidigt verktygsslitage och resultera i ojämna skärningar; Följaktligen inkluderar moderna rörelsekontroller ryckbegränsningsfunktioner. Inom maskinteknik övervägs ryck, förutom hastighet och acceleration, i utvecklingen av kamprofiler på grund av tribologiska implikationer och förmågan hos den aktiverade kroppen att följa kamprofilen utan prat . Ryck övervägs ofta när vibrationer är ett problem. En anordning som mäter ryck kallas "ryckmätare".

Ytterligare derivat

Huvudartikel: Fjärde, femte och sjätte derivator av position

Ytterligare tidsderivator har också namngetts, som snap eller jounce (fjärde derivata), crackle (femte derivata) och pop (sjätte derivata). Tidsderivator av positioner av högre ordning än fyra förekommer dock sällan.

Termerna snap , crackle och pop ‍—‌för fjärde, femte och sjätte derivatan av position‍—‌inspirerades av reklammaskoterna Snap, Crackle och Pop .

Se även

• Geomagnetiskt ryck
• Chock (mekanik)
• Ryck

•   Sprott JC (2003). Kaos och tidsserieanalys . Oxford University Press. ISBN 0-19-850839-5 .
• Sprott JC (1997). "Några enkla kaotiska ryckfunktioner" (PDF) . Am J Phys . 65 (6): 537–43. Bibcode : 1997AmJPh..65..537S . doi : 10.1119/1.18585 . Arkiverad från originalet (PDF) 2010-06-13 . Hämtad 2009-09-28 .
• Blair G (2005). "Making the Cam" (PDF) . Race Engine Technology (10) . Hämtad 2009-09-29 .

externa länkar

• Vilken term används för tredjederivatan av position? , beskrivning av jerk i Usenet Physics FAQ
• Matematik för rörelsekontrollprofiler
• Hiss-Ride-Kvalitet
• Hisstillverkare broschyr
• Patent av Wiener Kurve
• (på tyska) Beskrivning av Wiener Kurve