Vinkelhastighet

Vinkelhastighet
Vanliga symboler	ω
I SI-basenheter	s −1
Omfattande ?	ja
Intensiv ?	ja ( endast för stel kropp )
Konserverad ?	Nej
Beteende under koordinationsförändring	pseudovektor
Härledningar från andra kvantiteter	ω = d θ / d t
Dimensionera	${\mathsf {T}}^{-1}$

Inom fysiken är vinkelhastighet eller rotationshastighet ( ω eller Ω ), även känd som vinkelfrekvensvektor , en pseudovektorrepresentation av hur snabbt ett objekts vinkelposition eller orientering ändras med tiden (dvs. hur snabbt ett objekt roterar eller roterar i förhållande till en punkt eller axel). Storleken på pseudovektorn representerar vinkelhastigheten , hastigheten med vilken föremålet roterar eller roterar, och dess riktning är normal till det momentana rotationsplanet eller vinkelförskjutningen. Orienteringen av vinkelhastigheten specificeras konventionellt av högerregeln .

Det finns två typer av vinkelhastighet.

• Orbital vinkelhastighet avser hur snabbt ett punktobjekt kretsar kring ett fast origo , dvs. tidshastigheten för förändring av dess vinkelposition i förhållande till origo .
• Spinnvinkelhastighet avser hur snabbt en stel kropp roterar med avseende på dess rotationscentrum och är oberoende av valet av ursprung, i motsats till orbital vinkelhastighet.

I allmänhet har vinkelhastighet dimension av vinkel per tidsenhet (vinkel som ersätter avstånd från linjär hastighet med tid gemensamt). SI -enheten för vinkelhastighet är radianer per sekund , där radianen är en dimensionslös storhet , därför kan SI-enheterna för vinkelhastighet anges som s ⁻¹ . Vinkelhastigheten representeras vanligtvis av symbolen omega ( ω , ibland Ω ). Enligt konvention indikerar positiv vinkelhastighet rotation moturs , medan negativ är medurs.

Till exempel fullföljer en geostationär satellit en omloppsbana per dag ovanför ekvatorn , eller 360 grader per 24 timmar, och har vinkelhastighet ω = (360°)/(24 h) = 15°/h, eller (2π rad)/( 24 h) ≈ 0,26 rad/h. Om vinkeln mäts i radianer är den linjära hastigheten radien gånger vinkelhastigheten, $v=r\omega$ . Med en omloppsradie 42 000 km från jordens centrum är satellitens hastighet genom rymden alltså v = 42 000 km × 0,26/h ≈ 11 000 km/h. Vinkelhastigheten är positiv eftersom satelliten färdas österut med jordens rotation (moturs ovanför nordpolen.)

Orbital vinkelhastighet för en punktpartikel

Partikel i två dimensioner

Vinkelhastigheten för partikeln vid P med avseende på origo O bestäms av den vinkelräta komponenten av hastighetsvektorn v .

I det enklaste fallet med cirkulär rörelse vid radien $r$ , med positionen given av vinkelförskjutningen $\phi (t)$ från x-axeln, är omloppsvinkelhastigheten hastigheten för ändring av vinkel med avseende på tid: ${\textstyle \omega ={\frac {d\phi }{dt}}}$ . Om $\phi$ mäts i radianer är båglängden från den positiva x-axeln runt cirkeln till partikeln $\ell =r\phi$ , och den linjära hastigheten är ${\textstyle v(t)={\frac {d\ell }{dt}}=r\omega (t)}$ , så att ${\textstyle \omega ={\frac {v}{r}}}$ .

I det allmänna fallet med en partikel som rör sig i planet är omloppsvinkelhastigheten den hastighet med vilken positionsvektorn relativt ett valt ursprung "sveper ut" vinkeln. Diagrammet visar positionsvektorn $\mathbf {r}$ från origo $O$ till en partikel $P$ , med dess polära koordinater $(r, \phi )$ . (Alla variabler är funktioner av tiden $t$ .) Partikeln har linjär hastighetsdelning som ${\displaystyle \mathbf {v} =\mathbf {v} _{\|}+\mathbf {v} _{\perp }} ,$ med radiell komponent $\mathbf {v} _{\|}$ parallell med radien, och den tvärradiala (eller tangentiella) komponenten $\mathbf {v} _{\perp }$ vinkelrätt mot radien. När det inte finns någon radiell komponent, rör sig partikeln runt ursprunget i en cirkel; men när det inte finns någon tvärradiell komponent, rör sig den i en rak linje från origo. Eftersom radiell rörelse lämnar vinkeln oförändrad, bidrar endast den tvärradiala komponenten av linjär hastighet till vinkelhastigheten.

Vinkelhastigheten ω är ändringshastigheten för vinkelpositionen med avseende på tid, som kan beräknas från den tvärradiala hastigheten som:

$\omega ={\frac {d\phi }{dt}}={\frac {v_{\perp }}{r}}.$

Här är den tvärradiala hastigheten $v_{\perp }$ teckenstorleken på ${\displaystyle \mathbf {v} _{\perp }} ,$ positiv för moturs rörelse, negativ för medurs. Att ta polära koordinater för den linjära hastigheten $\mathbf {v}$ ger magnituden $v$ (linjär hastighet) och vinkeln $\theta$ relativt radievektorn; i dessa termer, $v_{\perp }=v\sin(\theta )$ , så att

$\omega ={\frac {v\sin(\theta)}{r}}.$

Dessa formler kan härledas genom att $\mathbf {r} =(r\cos(\varphi ),r\sin(\varphi ))$ , är $r$ en funktion av avståndet till origo med avseende på tid, och $\varphi$ en funktion av vinkeln mellan vektorn och x-axeln. Då ${\textstyle {\frac {d\ }{dtbf {r} }}=({\dot {r}}\cos(\varphi )-r{\dot {\varphi }}\sin(\varphi),{\dot {r}}\sin(\varphi)+r{ \dot {\varphi }}\cos(\varphi ))}$ . Som är lika med ${\dot {r}}(\cos(\varphi ),\sin(\varphi ))+r{\dot {\varphi }}(-\sin(\varphi ),\cos(\varphi ) )={\dot {r}}{\hat {r}}+r{\dot {\varphi }}{\hat {\varphi }}$ . (Se Enhetsvektor i cylindriska koordinater). Genom att veta ${\textstyle {\frac {d\mathbf {r} }{dt}}=\mathbf {v} } drar$ vi slutsatsen att den radiella komponenten av hastigheten ges av ${\dot {r}}$ , eftersom ${\hat {r}}$ är en radiell enhetsvektor; och den vinkelräta komponenten ges av $r{\dot {\varphi }}$ eftersom ${\hat {\varphi }}$ är en vinkelrät enhetsvektor.

I två dimensioner är vinkelhastighet ett tal med plus- eller minustecken som indikerar orientering, men som inte pekar i en riktning. Tecknet anses konventionellt vara positivt om radievektorn vrids moturs och negativt om medurs. Vinkelhastigheten kan då kallas en pseudoskalär , en numerisk storhet som ändrar tecken under en paritetsinversion , som att invertera en axel eller byta de två axlarna.

Partikel i tre dimensioner

Den orbitala vinkelhastighetsvektorn kodar tidshastigheten för förändring av vinkelposition, såväl som det momentana planet för vinkelförskjutning. I detta fall (moturs cirkulär rörelse) pekar vektorn uppåt.

I det tredimensionella rummet har vi återigen positionsvektorn r för en rörlig partikel. Här är omloppsvinkelhastigheten en pseudovektor vars magnitud är den hastighet med vilken r sveper ut vinkeln, och vars riktning är vinkelrät mot det momentana plan i vilket r sveper ut vinkeln (dvs planet som spänns över av r och v ). Men eftersom det finns två riktningar vinkelräta mot vilket plan som helst, ett ytterligare villkor är nödvändigt för att unikt specificera riktningen för vinkelhastigheten; konventionellt används högerregeln .

Låt pseudovektorn $\mathbf {u}$ vara enhetsvektorn vinkelrät mot planet som spänns av r och v , så att högerregeln är uppfylld (dvs. den momentana riktningen för vinkelförskjutningen är moturs sett från toppen av $\mathbf {u}$ ). Om man tar polära koordinater $(r,\phi )$ i detta plan, som i det tvådimensionella fallet ovan, kan man definiera den orbitala vinkelhastighetsvektorn som:

${\boldsymbol {\omega }}=\omega \mathbf {u} ={\frac {d\phi }{dt }}\mathbf {u} ={\frac {v\sin(\theta )}{r}}\mathbf {u} ,$

där θ är vinkeln mellan r och v . När det gäller korsprodukten är detta:

${\boldsymbol {\omega }}={\frac {\mathbf {r} \times \mathbf {v} }{r^{2}}}.$

Från ovanstående ekvation kan man återställa tangentiell hastighet som:

$\mathbf {v} _{\perp }={\boldsymbol {\omega }}\times \mathbf {r}$

Spinnvinkelhastighet för en stel kropp eller referensram

Givet en roterande ram med tre enhetskoordinatvektorer måste alla tre ha samma vinkelhastighet vid varje ögonblick. I en sådan ram kan varje vektor betraktas som en rörlig partikel med konstant skalär radie.

Den roterande ramen uppträder i samband med stela kroppar , och specialverktyg har utvecklats för den: spinnvinkelhastigheten kan beskrivas som en vektor eller motsvarande som en tensor .

I överensstämmelse med den allmänna definitionen definieras spinnvinkelhastigheten för en ram som den orbitala vinkelhastigheten för någon av de tre vektorerna (samma för alla) med avseende på dess eget rotationscentrum. Tillägget av vinkelhastighetsvektorer för ramar definieras också av den vanliga vektoradditionen (sammansättning av linjära rörelser), och kan vara användbart för att dekomponera rotationen som i en kardan . Alla komponenter i vektorn kan beräknas som derivator av parametrarna som definierar de rörliga ramarna (Euler-vinklar eller rotationsmatriser). Som i det allmänna fallet är addition kommutativ: $\omega _{1}+\omega _{2}=\omega _{2}+\omega _{1}$ .

Enligt Eulers rotationssats har varje roterande ram en momentan rotationsaxel , som är riktningen för vinkelhastighetsvektorn, och storleken på vinkelhastigheten är förenlig med det tvådimensionella fallet.

Om vi ​​väljer en referenspunkt ${\boldsymbol {R}}$ fixerad i den stela kroppen, är hastigheten ${\dot {\boldsymbol {r}}}$ för vilken punkt som helst i kroppen getts av

${\dot {\boldsymbol {r}}}={\dot {\boldsymbol {R}}}+{\boldsymbol {\omega }}\ gånger ({\boldsymbol {r}}-{\boldsymbol {R}})$

Komponenter från basvektorerna för en kroppsfixerad ram

Betrakta en stel kropp som roterar runt en fast punkt O. Konstruera en referensram i kroppen som består av en ortonormal uppsättning vektorer $\mathbf {e} _{1},\mathbf {e } _{2},\mathbf {e} _{3}$ fixerade till kroppen och med deras gemensamma ursprung vid O. Spinnvinkelhastighetsvektorn för både ram och kropp om O är då

${\boldsymbol {\omega }}=\left({\dot {\mathbf {e} }}_{1}\cdot \mathbf {e} _{2}\right)\mathbf {e} _ {3}+\left({\dot {\mathbf {e} }}_{2}\cdot \mathbf {e} _{3}\right)\mathbf {e} _{1}+\left({ \dot {\mathbf {e} }}_{3}\cdot \mathbf {e} _{1}\right)\mathbf {e} _{2},$

där ${\dot {\mathbf {e} }}_{i}={\frac {d\mathbf {e} _{i}}{dt}}$ är tidshastigheten för förändring av ramvektorn $\mathbf {e} _{i},i=1,2,3,$ på grund av rotationen.

Observera att denna formel är inkompatibel med uttrycket för omloppsvinkelhastighet

${\boldsymbol {\omega }}={\frac {\mathbf {r} \times \mathbf {v} }{r^{2}}},$

eftersom den formeln definierar vinkelhastighet för en enda punkt kring O, medan formeln i detta avsnitt gäller för en ram eller stel kropp. I fallet med en stel kropp måste en enda ${\boldsymbol {\omega }}$ redogöra för rörelsen för alla partiklar i kroppen.

Komponenter från Euler-vinklar

Diagram som visar Euler-ramen i grönt

Komponenterna i spinnvinkelhastighetspseudovektorn beräknades först av Leonhard Euler med hjälp av hans Euler-vinklar och användningen av en mellanliggande ram:

• En axel i referensramen (precessionsaxeln)
• Linjen med noder för den rörliga ramen med avseende på referensramen (nutationsaxel)
• En axel för den rörliga ramen (den inneboende rotationsaxeln)

Euler bevisade att projektionerna av vinkelhastighetspseudovektorn på var och en av dessa tre axlar är derivatan av dess associerade vinkel (vilket motsvarar att sönderdela den momentana rotationen i tre momentana Eulerrotationer ) . Därför:

${\boldsymbol {\omega }}={\dot {\alpha }}\mathbf {u} _{1}+{\dot { \beta }}\mathbf {u} _{2}+{\dot {\gamma }}\mathbf {u} _{3}$

Denna bas är inte ortonormal och den är svår att använda, men nu kan hastighetsvektorn ändras till den fasta ramen eller till den rörliga ramen med bara ett byte av baser. Till exempel, byta till den mobila ramen:

${\boldsymbol {\omega }}=({\dot {\alpha }}\sin \beta \sin \gamma +{\dot {\beta }}\cos \gamma ){\hat {\mathbf { i} }}+({\dot {\alpha }}\sin \beta \cos \gamma -{\dot {\beta }}\sin \gamma ){\hat {\mathbf {j} }}+({ \dot {\alpha }}\cos \beta +{\dot {\gamma }}){\hat {\mathbf {k} }}$

där ${\displaystyle {\hat {\mathbf {i} }},{\hat {\mathbf {j} }},{\hat {\mathbf {k} }}} är$ enheter vektorer för ramen fixerad i den rörliga kroppen. Detta exempel har gjorts med hjälp av ZXZ-konventionen för Euler-vinklar.

Tensor

Se även: Skevsymmetrisk matris

Vinkelhastighetsvektorn ${\boldsymbol {\omega }}=(\omega _{x},\omega _{y},\omega _{z})$ definierad ovan kan uttryckas ekvivalent som en vinkelhastighetstensor , matrisen (eller linjär mappning) W = W ( t ) definierad av:

$W={\begin{pmatrix}0&-\omega _{z}&\omega _{y}\\\omega _ {z}&0&-\omega _{x}\\-\omega _{y}&\omega _{x}&0\\\end{pmatrix}}$

Detta är en infinitesimal rotationsmatris . Den linjära avbildningen W fungerar som $({\boldsymbol {\omega }}\times )$ :

${\boldsymbol {\omega }}\times \mathbf {r} =W\cdot \mathbf {r} .$

Beräkning från orienteringsmatrisen

En vektor $\mathbf {r}$ som genomgår enhetlig cirkulär rörelse runt en fast axel uppfyller:

${\frac {d\mathbf {r} }{dt}}={\boldsymbol {\omega }}\times \mathbf {r} =W\cdot \mathbf {r}$

Givet orienteringsmatrisen A ( t ) för en ram, vars kolumner är de rörliga ortonormala koordinatvektorerna $\mathbf {e} _{1},\mathbf {e} _{2} ,\mathbf {e} _{3}$ , kan vi få dess vinkelhastighetstensor W ( t ) enligt följande. Vinkelhastigheten måste vara densamma för de tre vektorerna $\mathbf {r} =\mathbf {e} _{i}$ , så att ordna de tre vektorekvationerna i kolumner i en matris, har vi:

${\frac {dA}{dt}}=W\cdot A.$

(Detta gäller även om A ( t ) inte roterar jämnt.) Därför är vinkelhastighetstensorn:

$W={\frac {dA}{dt}}\cdot A^{-1}={\frac {dA}{ dt}}\cdot A^{\mathrm {T} },$

eftersom inversen av den ortogonala matrisen $A$ är dess transponering $A^{\mathrm {T} }$ .

Egenskaper

Se även: Infinitesimal rotation

I allmänhet är vinkelhastigheten i ett n -dimensionellt utrymme tidsderivatan av vinkelförskjutningstensorn, som är en snedsymmetrisk tensor i andra rang .

Denna tensor W kommer att ha n ( n −1)/2 oberoende komponenter, vilket är dimensionen av Lie-algebra i Lie-gruppen av rotationer i ett n -dimensionellt inre produktrum.

Dualitet med avseende på hastighetsvektorn

I tre dimensioner kan vinkelhastigheten representeras av en pseudovektor eftersom andra rangstensorer är dubbla till pseudovektorer i tre dimensioner. Eftersom vinkelhastighetstensorn W = W ( t ) är en skevsymmetrisk matris :

$W={\begin{pmatrix}0&-\omega _{z}&\omega _{y}\\\omega _{z}&0&-\omega _{x}\\-\omega _{y}&\omega _{x}&0\\\end{pmatrix}},$

dess Hodge-dual är en vektor, som är exakt den föregående vinkelhastighetsvektorn ${\boldsymbol {\omega }}=[\omega _{x},\omega _ {y},\omega _{z}]$ .

Exponentiell av W

Om vi ​​känner till en initial ram A (0) och vi får en konstant vinkelhastighetstensor W , kan vi få A ( t ) för vilken given t som helst . Kom ihåg matrisdifferentialekvationen:

${\frac {dA}{dt}}=W\cdot A.$

Denna ekvation kan integreras för att ge:

$A(t)=e^{Wt}A(0),$

som visar ett samband med Lie-gruppen av rotationer.

W är snedsymmetrisk

Vi bevisar att vinkelhastighetstensor är skevsymmetrisk , dvs $W={\frac {dA(t)}{dt}}\cdot A^{\text{T }}$ uppfyller $W^{\text{T}}=-W$ .

En rotationsmatris A är ortogonal, invers till dess transponering, så vi har $I=A\cdot A^{\text{T}}$ . För $A=A(t)$ ger en rammatris, med tidsderivatan av ekvationen:

$0={\frac {dA}{dt}}A^{\text{T}}+A{\frac {dA^{\text{ T}}}{dt}}$

Genom att använda formeln $(AB)^{\text{T}}=B^{\text{T}}A^{\text{T}}$ ,

$0={\frac {dA}{dt}}A^{\text{T}}+\left( {\frac {dA}{dt}}A^{\text{T}}\right)^{\text{T}}=W+W^{\text{T}}$

Således är W det negativa av dess transponering, vilket antyder att den är skevsymmetrisk.

Koordinatfri beskrivning

Vid varje ögonblick $t$ representerar vinkelhastighetstensorn en linjär karta mellan positionsvektorn $\mathbf {r} (t)$ och hastighetsvektorerna $\ mathbf {v} (t)$ av en punkt på en stel kropp som roterar runt origo:

$\mathbf {v} =W\mathbf {r} .$

Relationen mellan denna linjära karta och vinkelhastighetspseudovektorn ω $\displaystyle {\boldsymbol {\omega }}}$ är följande.

Eftersom W är derivatan av en ortogonal transformation , den bilinjära formen

$B(\mathbf {r} ,\mathbf {s} )=(W\mathbf {r} )\cdot \mathbf {s}$

är snedsymmetrisk . Således kan vi tillämpa det faktum av yttre algebra att det finns en unik linjär form $L$ på $\Lambda ^{2}V$ som

$L(\mathbf {r} \wedge \mathbf {s} )=B(\mathbf {r} ,\mathbf {s} )$

där $\mathbf {r} \wedge \mathbf {s} \in \Lambda ^{2}V$ är den yttre produkten av $\mathbf {r}$ och $\mathbf {s}$ .

Genom att ta det skarpa L ^♯ av L får vi

$(W\mathbf {r} )\cdot \mathbf {s} =L^{\sharp }\cdot (\mathbf {r} \wedge \mathbf {s} )$

Vi introducerar ${\displaystyle {\boldsymbol {\omega }}:={\star }(L^{\sharp })} ,$ som Hodge-dual av L ^♯ , och tillämpar definitionen av Hodge dual två gånger förutsatt att den föredragna enheten 3-vektor är $\star 1$

$(W\mathbf {r} )\cdot \mathbf {s} ={\star }({\star }(L^{\sharp })\wedge \mathbf {r} \wedge \mathbf {s} )={\star }({\boldsymbol {\omega }}\wedge \mathbf {r} \wedge \mathbf {s} )={\star }({\boldsymbol {\omega }}\wedge \mathbf {r } )\cdot \mathbf {s} =({\boldsymbol {\omega }}\times \mathbf {r} )\cdot \mathbf {s} ,$

var

${\boldsymbol {\omega }}\times \mathbf {r} :={\star }({\boldsymbol {\omega }}\wedge \mathbf {r } )$

per definition.

Eftersom $\mathbf {s}$ är en godtycklig vektor, följer från icke-degeneration av skalär produkt

$W\mathbf {r} ={\boldsymbol {\omega }}\times \mathbf {r}$

Vinkelhastighet som ett vektorfält

Eftersom spinnvinkelhastighetstensorn för en stel kropp (i dess viloram) är en linjär transformation som mappar positioner till hastigheter (inom den stela kroppen), kan den betraktas som ett konstant vektorfält . Speciellt är spinnvinkelhastigheten ett dödande vektorfält som tillhör ett element i Lie-algebra SO(3) i den 3-dimensionella rotationsgruppen SO(3) .

Det kan också visas att spinnvinkelhastighetsvektorfältet är exakt hälften av kurvan för det linjära hastighetsvektorfältet v ( r ) för den stela kroppen. I symboler,

${\boldsymbol {\omega }}={\frac {1}{2}}\nabla \times \mathbf {v}$

Stela kroppsöverväganden

Se även: axekonventioner

Position för punkt P i den stela kroppen (visas i blått). R _i är positionen med avseende på labbramen, centrerad vid O och ri _är positionen med avseende på den stela kroppsramen, centrerad vid O ′ . Ursprunget för den stela kroppsramen är vid vektorposition R från labbramen.

Samma ekvationer för vinkelhastigheten kan erhållas resonemang över en roterande stel kropp . Här antas inte att den stela kroppen roterar runt origo. Istället kan den antas rotera runt en godtycklig punkt som rör sig med en linjär hastighet V ( t ) i varje ögonblick.

För att få ekvationerna är det lämpligt att föreställa sig en stel kropp fäst vid ramarna och överväga ett koordinatsystem som är fixerat med avseende på den stela kroppen. Sedan ska vi studera koordinattransformationerna mellan denna koordinat och det fasta "laboratorie"-systemet.

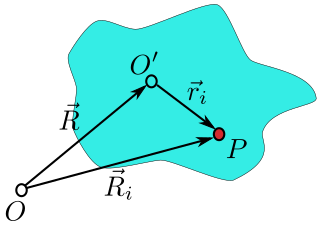
Som visas i figuren till höger är labbsystemets ursprung vid punkt O , det stela kroppssystemets ursprung är vid O ′ och vektorn från O till O ′ är R . En partikel ( i ) i den stela kroppen är belägen vid punkt P och vektorpositionen för denna partikel är R _i i labbramen och vid position ri _i kroppsramen. Man ser att partikelns position kan skrivas:

$\mathbf {R} _{i}=\mathbf {R} +\mathbf {r} _{i}$

Det avgörande kännetecknet för en stel kropp är att avståndet mellan två godtyckliga punkter i en stel kropp är oföränderligt i tiden. Detta betyder att längden på vektorn $\mathbf {r} _{i}$ är oförändrad. Med Eulers rotationssats kan vi ersätta vektorn $\mathbf {r} _{i}$ med ${\mathcal {R}}\mathbf {r} _{io}$ där ${\mathcal {R}}$ är en 3×3 rotationsmatris och $\mathbf {r} _{io}$ är partikelns position vid någon bestämd tidpunkt, säg t = 0 . Den här ersättningen är användbar, eftersom det nu bara är rotationsmatrisen ${\mathcal {R}}$ som ändras med tiden och inte referensvektorn $\mathbf {r} _{io}$ , när den stela kroppen roterar kring punkten O ′ . Dessutom, eftersom de tre kolumnerna i rotationsmatrisen representerar de tre versorerna av en referensram som roterar tillsammans med den stela kroppen, blir varje rotation kring valfri axel nu synlig, medan vektorn $\mathbf {r} _{i}$ inte skulle rotera om rotationsaxeln var parallell med den, och följaktligen skulle den endast beskriva en rotation kring en axel vinkelrät mot den (dvs. den skulle inte se komponenten av vinkelhastighetspseudovektorn parallell med den, och skulle endast tillåta beräkningen av komponenten vinkelrät mot den). Partikelns position skrivs nu som:

$\mathbf {R} _{i}=\mathbf {R} +{\mathcal {R}}\mathbf {r} _{io}$

Att ta tidsderivatan ger partikelns hastighet:

$\mathbf {V} _{i}=\mathbf {V} +{\frac {d{\mathcal {R}}}{dt}}\mathbf {r} _{io}$

där V _i är partikelns hastighet (i labbramen) och V är hastigheten för O ′ (ursprunget till den stela kroppsramen). Eftersom ${\mathcal {R}}$ är en rotationsmatris är dess invers dess transponering. Så vi ersätter ${\mathcal {I}}={\mathcal {R}}^{\text{T}}{\mathcal {R}}$ :

$\mathbf {V} _{i}=\mathbf {V} +{\frac {d{\mathcal {R}}}{dt}}{ \mathcal {I}}\mathbf {r} _{io}$

$\mathbf {V} _{i}=\mathbf {V} + {\frac {d{\mathcal {R}}}{dt}}{\mathcal {R}}^{\text{T}}{\mathcal {R}}\mathbf {r} _{io}$

$\mathbf {V} _{i}=\mathbf {V} +{\frac {d{\mathcal {R}}}{dt}}{\mathcal {R} }^{\text{T}}\mathbf {r} _{i}$

eller

$\mathbf {V} _{i}=\mathbf {V} +W\mathbf {r} _{i}$

där ${\displaystyle W={\frac {d{\mathcal {R}}}{dt}}{\mathcal {R}}^{\text{T}}} är det$ föregående vinkelhastighetstensor .

Det kan bevisas att detta är en skev symmetrisk matris , så vi kan ta dess dubbla för att få en 3-dimensionell pseudovektor som är exakt den föregående vinkelhastighetsvektorn ${\boldsymbol {\omega }}$ :

${\boldsymbol {\omega }}=[\omega _{x},\omega _{y},\omega _{z}]$

Ersätter W med ω i ovanstående hastighetsuttryck och ersätter matrismultiplikation med en ekvivalent korsprodukt:

$\mathbf {V} _{i}=\mathbf {V} +{\boldsymbol {\omega }}\times \mathbf {r} _{i}$

Det kan ses att hastigheten för en punkt i en stel kropp kan delas in i två termer - hastigheten för en referenspunkt fixerad i den stela kroppen plus tvärprodukttermen som involverar partikelns omloppsvinkelhastighet i förhållande till referensen punkt. Denna vinkelhastighet är vad fysiker kallar "snurrvinkelhastigheten" för den stela kroppen, i motsats till den orbitala vinkelhastigheten för referenspunkten O ′ omkring origo O .

Konsistens

Vi har antagit att den stela kroppen roterar runt en godtycklig punkt. Vi bör bevisa att den tidigare definierade spinnvinkelhastigheten är oberoende av valet av ursprung, vilket betyder att spinnvinkelhastigheten är en inneboende egenskap hos den spinnstyva kroppen. (Observera den markanta kontrasten av detta med omloppsvinkelhastigheten för en punktpartikel, vilket säkert beror på valet av ursprung.)

Bevisar oberoendet av spinnvinkelhastighet från val av ursprung

Se grafen till höger: Ursprunget för labbramen är O , medan O ₁ och O ₂ är två fasta punkter på den stela kroppen, vars hastighet är $\mathbf {v} _{1}$ och $\mathbf {v} _{2}$ respektive. Antag att vinkelhastigheten med avseende på O ₁ och O ₂ är ${\boldsymbol {\omega }}_{1}$ och ${\boldsymbol {\omega }}_{2}$ respektive. Eftersom punkt P och O ₂ bara har en hastighet,

$\mathbf {v} _{1}+{\boldsymbol {\omega }}_{1}\times \mathbf {r} _ {1}=\mathbf {v} _{2}+{\boldsymbol {\omega }}_{2}\times \mathbf {r} _{2}$

$\mathbf {v} _{2}=\mathbf {v} _{1}+{\boldsymbol {\omega }}_{1}\times \mathbf {r} =\mathbf {v} _{ 1}+{\boldsymbol {\omega }}_{1}\times (\mathbf {r} _{1}-\mathbf {r} _{2})$

Ovanstående två ger det

$({\boldsymbol {\omega }}_{2}-{\boldsymbol {\omega }}_{1})\times \mathbf {r} _{ 2}=0$

Eftersom punkten P (och därmed $\mathbf {r} _{2}$ ) är godtycklig, följer det att

${\boldsymbol {\omega }}_{1}={\boldsymbol {\omega }}_{2}$

Om referenspunkten är den momentana rotationsaxeln kommer uttrycket av hastigheten för en punkt i den stela kroppen att ha bara vinkelhastighetstermen. Detta beror på att hastigheten för den momentana rotationsaxeln är noll. Ett exempel på den momentana rotationsaxeln är gångjärnet på en dörr. Ett annat exempel är kontaktpunkten för en rent rullande sfärisk (eller mer allmänt konvex) stel kropp.

Se även

• Vinkelacceleration
• Vinkelfrekvens
• Vinkelmoment
• Arealhastighet
• Isometri
• Ortogonal grupp
• Styv kroppsdynamik
• Vorticity

•   Symon, Keith (1971). Mekanik . Addison-Wesley, Reading, MA. ISBN 978-0-201-07392-8 .
•   Landau, LD ; Lifshitz, EM (1997). Mekanik . Butterworth-Heinemann. ISBN 978-0-7506-2896-9 .

externa länkar

• En lärobok i fysik av Arthur Lalanne Kimball ( Angular Velocity of a particle )
• Pickering, Steve (2009). "ω Rotationshastighet [vinkelhastighet]" . Sextio symboler . Brady Haran för University of Nottingham .