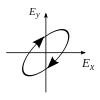Polarisering (fysik)

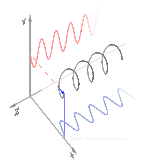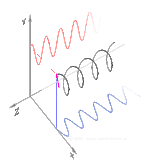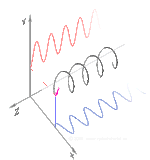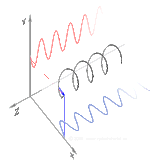
Cirkulär polarisering på gummitråd, omvandlad till linjär polarisation

Polarisation ( även polarisation ) är en egenskap hos transversella vågor som specificerar den geometriska orienteringen av svängningarna . I en tvärvåg är oscillationens riktning vinkelrät mot vågens rörelseriktning. Ett enkelt exempel på en polariserad tvärvåg är vibrationer som rör sig längs en spänd sträng ( se bild) ; till exempel i ett musikinstrument som en gitarrsträng . Beroende på hur snöret är plockat kan vibrationerna vara i vertikal riktning, horisontell riktning eller i vilken vinkel som helst vinkelrätt mot snöret. I motsats till detta, i longitudinella vågor , såsom ljudvågor i en vätska eller gas, är förskjutningen av partiklarna i oscillationen alltid i utbredningsriktningen, så dessa vågor uppvisar inte polarisering. Tvärgående vågor som uppvisar polarisering inkluderar elektromagnetiska vågor som ljus- och radiovågor , gravitationsvågor och tvärgående ljudvågor ( skjuvvågor ) i fasta ämnen.

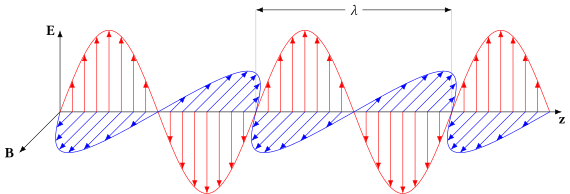
En elektromagnetisk våg som ljus består av ett kopplat oscillerande elektriskt fält och magnetfält som alltid är vinkelräta mot varandra; enligt konvention hänvisar "polariseringen" av elektromagnetiska vågor till det elektriska fältets riktning. I linjär polarisation svänger fälten i en enda riktning. I cirkulär eller elliptisk polarisation roterar fälten med en konstant hastighet i ett plan när vågen färdas, antingen i höger eller vänster riktning.

Ljus eller annan elektromagnetisk strålning från många källor, såsom solen, lågorna och glödlampor , består av kortvågståg med en lika stor blandning av polarisationer; detta kallas opolariserat ljus . Polariserat ljus kan produceras genom att passera opolariserat ljus genom en polarisator , som tillåter vågor av endast en polarisation att passera igenom. De vanligaste optiska materialen påverkar inte ljusets polarisering, men vissa material - de som uppvisar dubbelbrytning , dikroism eller optisk aktivitet - påverkar ljuset olika beroende på dess polarisering. Vissa av dessa används för att tillverka polariserande filter. Ljus blir också delvis polariserat när det reflekteras i en vinkel från en yta.

Enligt kvantmekaniken kan elektromagnetiska vågor också ses som strömmar av partiklar som kallas fotoner . När den ses på detta sätt bestäms polariseringen av en elektromagnetisk våg av en kvantmekanisk egenskap hos fotoner som kallas deras spin . En foton har en av två möjliga snurr: den kan antingen snurra i höger eller vänster riktning om sin färdriktning. Cirkulärt polariserade elektromagnetiska vågor är sammansatta av fotoner med endast en typ av spinn, antingen höger- eller vänsterhand. Linjärt polariserade vågor består av fotoner som är i en överlagring av höger och vänster cirkulärt polariserade tillstånd, med lika amplitud och faser synkroniserade för att ge oscillation i ett plan.

Polarisering är en viktig parameter inom vetenskapsområden som behandlar tvärgående vågor, såsom optik , seismologi , radio och mikrovågor . Särskilt påverkade är teknologier som lasrar , trådlös och optisk fibertelekommunikation och radar .

Introduktion

Vågutbredning och polarisering

korslinjärpolariserad

De flesta ljuskällor klassificeras som inkoherenta och opolariserade (eller endast "delvis polariserade") eftersom de består av en slumpmässig blandning av vågor som har olika rumsliga egenskaper, frekvenser (våglängder), faser och polarisationstillstånd. Men för att förstå elektromagnetiska vågor och polarisation i synnerhet är det lättare att bara överväga koherenta plana vågor ; dessa är sinusformade vågor i en viss riktning (eller vågvektor ), frekvens, fas och polarisationstillstånd. Att karakterisera ett optiskt system i förhållande till en plan våg med de givna parametrarna kan sedan användas för att förutsäga dess svar på ett mer generellt fall, eftersom en våg med vilken som helst specificerad rumslig struktur kan brytas ned till en kombination av plana vågor (dess s.k. vinkelspektrum ). Inkoherenta tillstånd kan modelleras stokastiskt som en viktad kombination av sådana okorrelerade vågor med viss fördelning av frekvenser (dess spektrum ), faser och polarisationer.

Tvärgående elektromagnetiska vågor

En "vertikalt polariserad" elektromagnetisk våg med våglängden λ har sin elektriska fältvektor E (röd) oscillerande i vertikal riktning. Magnetfältet B (eller H ) är alltid i rät vinkel mot det (blått), och båda är vinkelräta mot utbredningsriktningen ( z ).

Elektromagnetiska vågor (som ljus), som färdas i fritt utrymme eller annat homogent isotropiskt icke-dämpande medium, beskrivs korrekt som tvärgående vågor , vilket betyder att en plan vågs elektriska fältvektor E och magnetfält H är var och en i någon riktning vinkelräta mot (eller "tvärgående" mot) riktningen för vågutbredning; E och H är också vinkelräta mot varandra. Enligt konvention ges "polarisations"-riktningen för en elektromagnetisk våg av dess elektriska fältvektor. Med tanke på en monokromatisk plan våg med optisk frekvens f (ljus med vakuumvåglängd λ har frekvensen f = c/λ där c är ljusets hastighet), låt oss ta utbredningsriktningen som z -axeln. Eftersom E- och H -fälten _är Ez = H _z = 0 en tvärvåg måste då endast komponenter innehålla komponenter i x- och y -riktningarna medan . Med hjälp av komplex (eller fas ) notation, ges de momentana fysiska elektriska och magnetiska fälten av de reella delarna av de komplexa storheterna som förekommer i följande ekvationer. Som en funktion av tiden t och rumslig position z (eftersom för en plan våg i + z -riktningen fälten inte har något beroende av x eller y ) kan dessa komplexa fält skrivas som:

{\vec {E} }(z,t)={\begin{bmatrix}e_{x}\\e_{y}\\0\end{bmatrix}}\;e^{i2\pi \left({\frac {z}{ \lambda }}-{\frac {t}{T}}\right)}={\begin{bmatrix}e_{x}\\e_{y}\\0\end{bmatrix}}\;e^{ i(kz-\omega t)}

och

{\vec {H} }(z,t)={\begin{bmatrix}h_{x}\\h_{y}\\0\end{bmatrix}}\;e^{i2\pi \left({\frac {z}{ \lambda }}-{\frac {t}{T}}\right)}={\begin{bmatrix}h_{x}\\h_{y}\\0\end{bmatrix}}\;e^{ i(kz-\omega t)}

₀ där λ = λ / n är våglängden i mediet (vars brytningsindex är n ) och T = 1/ f är vågens period. Här e _x , e _y , h _x , och h _y komplexa tal. I den andra mer kompakta formen, som dessa ekvationer vanligtvis uttrycks, beskrivs dessa faktorer med hjälp av vågtalet k $\displaystyle k=2\pi n/\lambda _{0}}$ och vinkelfrekvens (eller "radianfrekvens") $\omega =2\pi f$ . I en mer allmän formulering med fortplantning som inte är begränsad till +z -riktningen, ersätts det rumsliga beroendet kz med ${\vec {k}}\cdot {\vec {r}}$ där ${\vec {k}}$ kallas vågvektorn , vars storlek är vågnumret.

Således innehåller de ledande vektorerna e och h var och en upp till två icke-noll (komplexa) komponenter som beskriver amplituden och fasen för vågens x- och y -polarisationskomponenter (återigen, det kan inte finnas någon z -polarisationskomponent för en transversell våg i + z -riktningen) . För ett givet medium med en karakteristisk impedans $\eta } är$ displaystyle h relaterad till e med:

h_{y}={\frac {e_{x}}{\eta }}

och

h_{x}=-{\frac {e_{y}}{\eta }}

.

₀₀ I ett dielektrikum är η reell och har värdet η / n , där n är brytningsindex och η är impedansen för fritt utrymme. Impedansen kommer att vara komplex i ett ledande medium. ^{[ förtydligande behövs ]} Observera att med tanke på det förhållandet måste punktprodukten av E och H vara noll: ^{[ tveksamt – diskutera ]}

{\vec {E}}\left({\vec {r}},t\right)\cdot {\vec {H}}\left({\vec {r}},t\right )=e_{x}h_{x}+e_{y}h_{y}+e_{z}h_{z}=e_{x}\left(-{\frac {e_{y}}{\eta } }\right)+e_{y}\left({\frac {e_{x}}{\eta }}\right)+0\cdot 0=0

vilket indikerar att dessa vektorer är ortogonala (i rät vinkel mot varandra), som förväntat.

Så genom att känna till utbredningsriktningen (+ z i detta fall) och η, kan man lika gärna specificera vågen i termer av att bara e _x och e _y beskriver det elektriska fältet. Vektorn som innehåller e _x och e _y (men utan z -komponenten som nödvändigtvis är noll för en transversell våg) är känd som en Jones-vektor . Förutom att specificera vågens polarisationstillstånd, specificerar en generell Jones-vektor också den övergripande magnituden och fasen för den vågen. Specifikt är ljusvågens intensitet proportionell mot summan av de kvadratiska magnituderna av de två elektriska fältkomponenterna:

I=\left(\left|e_{x}\right|^{2}+\left|e_{y}\right |^{2}\right)\,{\frac {1}{2\eta }}

Vågens polarisationstillstånd är dock endast beroende av det (komplexa ) förhållandet e _y till e _x . Så låt oss bara betrakta vågor vars |e _x | ² + |e _y | ² = 1 ; detta råkar motsvara en intensitet på cirka 0,00133 watt per kvadratmeter i ledigt utrymme (där $\eta =$ ${\displaystyle \eta _{0}} )$ . Och eftersom den absoluta fasen av en våg är oviktig för att diskutera dess polariseringstillstånd, låt oss bestämma att fasen för e _x är noll, med andra ord e _x är ett reellt tal medan e _y kan vara komplext. Under dessa begränsningar e _x och e _y representeras enligt följande:

e_{x}={\sqrt {\frac {1+Q}{2}}}

e_{y}= {\sqrt {\frac {1-Q}{2}}}\,e^{i\phi }

där polarisationstillståndet nu är helt parametriserat av värdet på Q (såsom −1 < Q < 1) och den relativa fasen $\phi$ .

Icke-tvärgående vågor

Förutom tvärvågor finns det många vågrörelser där svängningen inte är begränsad till riktningar vinkelräta mot utbredningsriktningen. Dessa fall ligger långt utanför ramen för den aktuella artikeln som koncentrerar sig på transversella vågor (som de flesta elektromagnetiska vågor i bulkmedia), men man bör vara medveten om fall där polariseringen av en koherent våg inte kan beskrivas enbart med hjälp av en Jones-vektor, som vi just har gjort.

Bara med tanke på elektromagnetiska vågor, noterar vi att den föregående diskussionen strikt gäller plana vågor i ett homogent isotropiskt icke-dämpande medium, medan i ett anisotropiskt medium (som dubbelbrytande kristaller som diskuteras nedan) kan det elektriska eller magnetiska fältet ha såväl longitudinella som magnetiska fält. tvärgående komponenter. I dessa fall följer den elektriska förskjutningen D och den magnetiska flödestätheten B ^{[ förtydligande behövs ]} fortfarande ovanstående geometri men på grund av anisotropi i den elektriska susceptibiliteten (eller i den magnetiska permeabiliteten ), nu given av en tensor , riktningen för E (eller H) ) kan skilja sig från det för D (eller B ). Även i isotropa medier kan så kallade inhomogena vågor sändas in i ett medium vars brytningsindex har en betydande imaginär del (eller " extinktionskoefficient ") såsom metaller; ^{[ förtydligande behövs ]} dessa fält är inte heller strikt tvärgående. Ytvågor eller vågor som fortplantar sig i en vågledare (som en optisk fiber ) är i allmänhet inte tvärgående vågor, utan kan beskrivas som ett elektriskt eller magnetiskt tvärläge , eller ett hybridläge.

Även i fritt utrymme kan longitudinella fältkomponenter genereras i fokalområden, där planvågsapproximationen bryts ner. Ett extremt exempel är radiellt eller tangentiellt polariserat ljus, i vars fokus det elektriska respektive magnetiska fältet är helt longitudinellt (längs utbredningsriktningen).

För longitudinella vågor som ljudvågor i vätskor är svängningsriktningen per definition längs färdriktningen, så frågan om polarisering nämns normalt inte ens. Å andra sidan kan ljudvågor i ett bulkfast ämne vara tvärgående såväl som longitudinella, för totalt tre polarisationskomponenter. I detta fall är den tvärgående polarisationen associerad med riktningen för skjuvspänningen och förskjutningen i riktningar vinkelräta mot utbredningsriktningen, medan den längsgående polarisationen beskriver komprimering av det fasta ämnet och vibration längs utbredningsriktningen. Den differentiella utbredningen av tvärgående och longitudinella polarisationer är viktig inom seismologi .

Polariseringstillstånd

Elektriskt fältsvängning

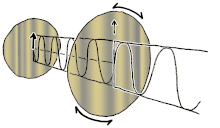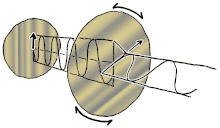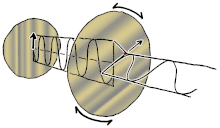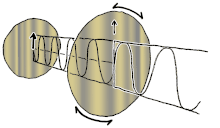
Polarisation förstås bäst genom att man initialt endast tar hänsyn till rena polarisationstillstånd och endast en koherent sinusformad våg vid någon optisk frekvens. Vektorn i det intilliggande diagrammet kan beskriva oscillationen av det elektriska fältet som emitteras av en singelmodslaser (vars oscillationsfrekvens vanligtvis skulle vara 10 ¹⁵ gånger snabbare). Fältet svänger i xy- planet, längs sidan, med vågen som utbreder sig i z- riktningen, vinkelrätt mot sidan. De två första diagrammen nedan spårar den elektriska fältvektorn över en fullständig cykel för linjär polarisation vid två olika orienteringar; dessa anses var och en vara ett distinkt polarisationstillstånd (SOP). Observera att den linjära polarisationen vid 45° också kan ses som tillägget av en horisontellt linjärt polariserad våg (som i bilden längst till vänster) och en vertikalt polariserad våg med samma amplitud i samma fas .

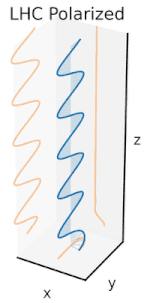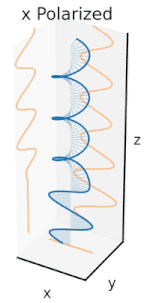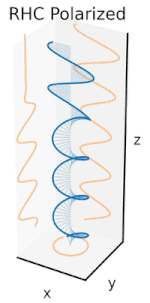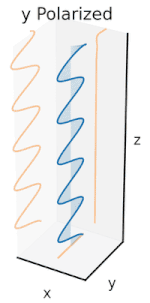
Animation som visar fyra olika polarisationstillstånd och tre ortogonala projektioner.

En cirkulärt polariserad våg som summan av två linjärt polariserade komponenter 90° ur fas

Om man nu skulle införa en fasförskjutning mellan dessa horisontella och vertikala polarisationskomponenter, skulle man i allmänhet få elliptisk polarisation som visas i den tredje figuren. När fasförskjutningen är exakt ±90° produceras cirkulär polarisation (fjärde och femte siffran). Sålunda skapas cirkulär polarisering i praktiken, som börjar med linjärt polariserat ljus och använder en kvartsvågsplatta för att införa en sådan fasförskjutning. Resultatet av två sådana fasförskjutna komponenter som orsakar en roterande elektrisk fältvektor visas i animationen till höger. Observera att cirkulär eller elliptisk polarisation kan involvera antingen en medurs eller moturs rotation av fältet. Dessa motsvarar distinkta polarisationstillstånd, såsom de två cirkulära polarisationerna som visas ovan.

Naturligtvis är orienteringen av x- och y -axlarna som används i denna beskrivning godtycklig. Valet av ett sådant koordinatsystem och betraktande av polarisationsellipsen i termer av x- och y -polarisationskomponenterna, motsvarar definitionen av Jones-vektorn (nedan) i termer av dessa baspolarisationer . Man skulle typiskt välja axlar för att passa ett speciellt problem som att x är i infallsplanet. Eftersom det finns separata reflektionskoefficienter för de linjära polarisationerna i och vinkelrät mot infallsplanet ( p- och s- polarisationer, se nedan), förenklar det valet avsevärt beräkningen av en vågs reflektion från en yta.

vilket par som helst av ortogonala polarisationstillstånd som basfunktioner, inte bara linjära polarisationer. Till exempel, att välja höger och vänster cirkulär polarisation som basfunktioner förenklar lösningen av problem som involverar cirkulär dubbelbrytning (optisk aktivitet) eller cirkulär dikroism.

Polarisationsellips

Betrakta en rent polariserad monokromatisk våg. Om man skulle plotta den elektriska fältvektorn över en svängningscykel, skulle en ellips i allmänhet erhållas, som visas i figuren, motsvarande ett särskilt tillstånd av elliptisk polarisation . Observera att linjär polarisation och cirkulär polarisation kan ses som speciella fall av elliptisk polarisation.

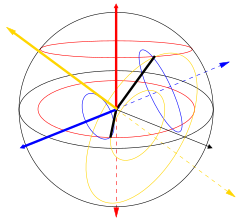
Ett polarisationstillstånd kan då beskrivas i relation till ellipsens geometriska parametrar, och dess "handedness", det vill säga om rotationen runt ellipsen är medurs eller moturs. En parametrisering av den elliptiska figuren specificerar orienteringsvinkeln ψ , definierad som vinkeln mellan ellipsens huvudaxel och x -axeln tillsammans med ellipticiteten ε = a/b , förhållandet mellan ellipsens huvudaxel och mindre axel. (även känt som det axiella förhållandet ). Ellipticitetsparametern är en alternativ parametrisering av en ellips excentricitet ${\textstyle e={\sqrt {1-b^{2}/a^{2}}},}$ eller ellipticity vinkel , ${\textstyle \chi =\arctan b/a}$ ${\textstyle =\arctan 1/\varepsilon }$ som visas i figuren. Vinkeln χ är också signifikant genom att latituden (vinkeln från ekvatorn) för polarisationstillståndet som representerat på Poincaré-sfären (se nedan) är lika med ±2 χ . De speciella fallen av linjär och cirkulär polarisation motsvarar en elliptisk ε av oändlighet och enhet (eller χ av noll respektive 45°).

Jones vektor

Fullständig information om ett helt polariserat tillstånd tillhandahålls också av amplituden och fasen av svängningar i två komponenter av den elektriska fältvektorn i polarisationsplanet. Denna representation användes ovan för att visa hur olika polariseringstillstånd är möjliga. Amplitud- och fasinformationen kan bekvämt representeras som en tvådimensionell komplex vektor ( Jones-vektorn) :

\mathbf {e} ={\begin{bmatrix}a_{1}e^{i\theta _{1}}\\a_{2}e^{i\theta _{2}}\end{ bmatrix}}.

Här betecknar $a_{1}$ och $a_{2}$ amplituden för vågen i de två komponenterna i den elektriska fältvektorn, medan $\theta _{1}$ och $\theta _{2}$ representerar faserna. Produkten av en Jones-vektor med ett komplext antal enhetsmoduler ger en annan Jones-vektor som representerar samma ellips och därmed samma polarisationstillstånd. Det fysiska elektriska fältet, som den verkliga delen av Jones-vektorn, skulle förändras men själva polariseringstillståndet är oberoende av den absoluta fasen . Basvektorerna som används för att representera Jones-vektorn behöver inte representera linjära polarisationstillstånd (dvs. vara verkliga ) . I allmänhet kan två ortogonala tillstånd användas, där ett ortogonalt vektorpar formellt definieras som ett med en inre produkt noll . Ett vanligt val är vänster och höger cirkulär polarisation, till exempel för att modellera den olika utbredningen av vågor i två sådana komponenter i cirkulärt dubbelbrytande media (se nedan) eller signalvägar för koherenta detektorer som är känsliga för cirkulär polarisation.

Koordinatram

Oavsett om polariseringstillståndet representeras med hjälp av geometriska parametrar eller Jones-vektorer, är koordinatramens orientering implicit i parametriseringen. Detta tillåter en viss grad av frihet, nämligen rotation kring utbredningsriktningen. När man betraktar ljus som utbreder sig parallellt med jordens yta, används ofta termerna "horisontell" och "vertikal" polarisering, där den förra är associerad med den första komponenten av Jones-vektorn, eller noll azimutvinkel. Å andra sidan, inom astronomi används i allmänhet det ekvatoriala koordinatsystemet istället, med nollazimut (eller positionsvinkel, som det mer allmänt kallas inom astronomi för att undvika förväxling med det horisontella koordinatsystemet ) som motsvarar rakt norrut.

s- och p- beteckningar

Elektromagnetiska vektorer för

{\textstyle {\textbf {E}}}

,

{\textstyle {\textbf {B}}}

och

{\textstyle {\textbf {k}}}

med

{\textstyle {\textbf {E}}={\textbf {E}}(x,y)}

tillsammans med 3 plana projektioner och en deformationsyta av totalt elektriskt fält. Ljuset är alltid s-polariserat i xy-planet.

{\textstyle \theta }

är den polära vinkeln för

{\textstyle {\textbf {k}}}

och

{\textstyle \varphi _{E}}

är azimutvinkeln för

{\textstyle {\textbf { E}}}

.

Ett annat koordinatsystem som ofta används hänför sig till infallsplanet . Detta är planet som skapas av den inkommande utbredningsriktningen och vektorn vinkelrät mot planet för ett gränssnitt, med andra ord, planet i vilket strålen färdas före och efter reflektion eller brytning. Komponenten av det elektriska fältet parallellt med detta plan kallas p-liknande (parallell) och komponenten vinkelrät mot detta plan kallas s-liknande (från senkrecht , tyska för vinkelrät). Polariserat ljus med sitt elektriska fält längs infallsplanet betecknas alltså p-polariserat , medan ljus vars elektriska fält är normalt mot infallsplanet kallas s-polariserat . P- polarisering kallas vanligen för transversell magnetisk (TM), och har också benämnts pi-polariserad eller tangentiellt plan polariserad . S- polarisering kallas också transversell-elektrisk (TE), såväl som sigma-polariserad eller sagittalplanspolariserad .

Grad av polarisering

Polarisationsgrad ( DOP ) är en storhet som används för att beskriva den del av en elektromagnetisk våg som är polariserad . En perfekt polariserad våg har en DOP på 100 %, medan en opolariserad våg har en DOP på 0 %. En våg som är delvis polariserad, och därför kan representeras av en överlagring av en polariserad och opolariserad komponent, kommer att ha en DOP någonstans mellan 0 och 100 %. DOP beräknas som andelen av den totala effekten som bärs av vågens polariserade komponent.

DOP kan användas för att kartlägga töjningsfältet i material när man överväger fotoluminescensens DOP . Polariseringen av fotoluminescensen är relaterad till töjningen i ett material genom det givna materialets fotoelasticitetstensor .

DOP visualiseras också med hjälp av Poincaré- sfärrepresentationen av en polariserad stråle. I denna representation är DOP lika med längden på vektorn mätt från sfärens mitt.

Opolariserat och delvis polariserat ljus

Opolariserat ljus är ljus med en slumpmässig, tidsvarierande polarisation. Naturligt ljus, som de flesta andra vanliga källor till synligt ljus, produceras oberoende av ett stort antal atomer eller molekyler vars utsläpp är okorrelerade . Denna term är något inexakt, eftersom det vid vilket ögonblick som helst på en plats finns ett bestämt polariseringsplan ; det innebär dock att polariseringen förändras så snabbt i tiden att den inte kommer att mätas eller relevant för resultatet av ett experiment.

Opolariserat ljus kan produceras från den inkoherenta kombinationen av vertikalt och horisontellt linjärt polariserat ljus, eller höger- och vänsterhänt cirkulärt polariserat ljus. Omvänt kan de två ingående linjärt polariserade tillstånden av opolariserat ljus inte bilda ett interferensmönster , även om de roteras i linje ( Fresnel–Arago 3:e lag) .

En så kallad depolarisator verkar på en polariserad stråle för att skapa en där polarisationen varierar så snabbt över strålen att den kan ignoreras i de avsedda tillämpningarna. Omvänt verkar en polarisator på en opolariserad stråle eller godtyckligt polariserad stråle för att skapa en som är polariserad.

Opolariserat ljus kan beskrivas som en blandning av två oberoende motsatt polariserade strömmar, var och en med halva intensiteten. Ljus sägs vara delvis polariserat när det finns mer kraft i en av dessa strömmar än den andra. Vid vilken speciell våglängd som helst kan partiellt polariserat ljus statistiskt beskrivas som superpositionen av en helt opolariserad komponent och en helt polariserad komponent. Man kan sedan beskriva ljuset i termer av graden av polarisation och parametrarna för den polariserade komponenten. Den polariserade komponenten kan beskrivas i termer av en Jones-vektor eller polarisationsellips. Men för att också beskriva graden av polarisation använder man normalt Stokes-parametrar för att specificera ett tillstånd av partiell polarisation.

Implikationer för reflektion och fortplantning

Polarisering i vågutbredning

I ett vakuum fortplantar sig komponenterna i det elektriska fältet med ljusets hastighet , så att vågens fas varierar i rum och tid medan polarisationstillståndet inte gör det. Det vill säga, den elektriska fältvektorn e för en plan våg i + z -riktningen följer:

\mathbf {e} (z+\Delta z,t+\Delta t) =\mathbf {e} (z,t)e^{ik(c\Delta t-\Delta z)},

där k är vågnumret . Som noterats ovan är det momentana elektriska fältet den reella delen av produkten av Jones-vektorn gånger fasfaktorn $e^{-i\omega t}$ . När en elektromagnetisk våg interagerar med materia, förändras dess utbredning enligt materialets (komplexa) brytningsindex . När den verkliga eller imaginära delen av det brytningsindexet är beroende av polarisationstillståndet för en våg, egenskaper kända som dubbelbrytning respektive polarisationsdikroism (eller diattenuation ), då kommer polarisationstillståndet för en våg i allmänhet att ändras.

I sådana medier kan en elektromagnetisk våg med vilket som helst givet polarisationstillstånd brytas upp i två ortogonalt polariserade komponenter som möter olika utbredningskonstanter . Effekten av utbredning över en given väg på dessa två komponenter karakteriseras lättast i form av en komplex 2×2 transformationsmatris J känd som en Jones-matris :

\mathbf {e'} =\mathbf {J} \mathbf {e} .

Jones-matrisen på grund av passage genom ett transparent material är beroende av utbredningsavståndet såväl som dubbelbrytningen. Dubbelbrytningen (liksom det genomsnittliga brytningsindexet) kommer i allmänhet att vara dispersiv , det vill säga den kommer att variera som en funktion av optisk frekvens (våglängd). I fallet med icke-dubbelbrytande material är dock 2×2 Jones-matrisen identitetsmatrisen (multiplicerad med en skalär fasfaktor och dämpningsfaktor), vilket innebär ingen förändring i polarisation under fortplantning.

För fortplantningseffekter i två ortogonala lägen kan Jones-matrisen skrivas som

\mathbf {J} =\mathbf {T} {\begin{bmatrix}g_{1}&0\\0&g_{2}\end{bmatrix}} \mathbf {T} ^{-1},

där g ₁ och g ₂ är komplexa tal som beskriver fasfördröjningen och möjligen amplituddämpningen på grund av utbredning i var och en av de två polarisationsegenmoden. T är en enhetlig matris som representerar en förändring av basen från dessa fortplantningsmoder till det linjära systemet som används för Jones-vektorerna; i fallet med linjär dubbelbrytning eller diattenuering är moden i sig linjära polarisationstillstånd så T och T ⁻¹ kan utelämnas om koordinataxlarna har valts på lämpligt sätt.

Dubbelbrytning

I ett dubbelbrytande ämne färdas elektromagnetiska vågor med olika polarisation med olika hastigheter ( fashastigheter) . Som ett resultat när opolariserade vågor färdas genom en platta av dubbelbrytande material, har en polarisationskomponent en kortare våglängd än den andra, vilket resulterar i en fasskillnad mellan komponenterna som ökar ju längre vågorna färdas genom materialet. Jones-matrisen är en enhetlig matris : | g ₁ | = | g ₂ | = 1. Medier som kallas diattenuerande (eller dikroiska i betydelsen polarisation), där endast amplituderna för de två polarisationerna påverkas differentiellt, kan beskrivas med hjälp av en hermitisk matris (i allmänhet multiplicerad med en gemensam fasfaktor). Faktum är att, eftersom vilken matris som helst kan skrivas som produkten av enhetliga och positiva hermitiska matriser, kan ljusutbredning genom vilken sekvens av polarisationsberoende optiska komponenter som helst skrivas som produkten av dessa två grundläggande typer av transformationer.

Färgmönster på en plastlåda som visar stressinducerad dubbelbrytning när den placeras mellan två korsade polarisatorer .

I dubbelbrytande media finns ingen dämpning, men två moder åstadkommer en differentiell fasfördröjning. Välkända manifestationer av linjär dubbelbrytning (det vill säga där baspolarisationerna är ortogonala linjära polarisationer) förekommer i optiska vågplattor /retardrar och många kristaller. Om linjärt polariserat ljus passerar genom ett dubbelbrytande material kommer dess polarisationstillstånd i allmänhet att förändras, om inte dess polarisationsriktning är identisk med en av dessa baspolarisationer. Eftersom fasförskjutningen, och därmed förändringen i polarisationstillståndet, vanligtvis är våglängdsberoende, kan sådana föremål som ses i vitt ljus mellan två polarisatorer ge upphov till färgglada effekter, som ses i det medföljande fotografiet.

Cirkulär dubbelbrytning benämns också optisk aktivitet , speciellt i kirala vätskor, eller Faraday-rotation , när det beror på närvaron av ett magnetiskt fält längs utbredningsriktningen. När linjärt polariserat ljus passerar genom ett sådant föremål, kommer det att lämnas fortfarande linjärt polariserat, men med polarisationsaxeln roterad. En kombination av linjär och cirkulär dubbelbrytning kommer att ha två ortogonala elliptiska polarisationer som baspolarisationer; termen "elliptisk dubbelbrytning" används emellertid sällan.

Vägar tagna av vektorer i Poincaré-sfären under dubbelbrytning. Utbredningssätten (rotationsaxlarna) visas med röda, blå och gula linjer, de initiala vektorerna med tjocka svarta linjer och vägarna de tar med färgade ellipser (som representerar cirklar i tre dimensioner).

Man kan visualisera fallet med linjär dubbelbrytning (med två ortogonala linjära utbredningslägen) med en inkommande våg linjärt polariserad i en 45° vinkel mot dessa moder. När en differentialfas börjar ackumuleras blir polarisationen elliptisk, och så småningom ändras den till ren cirkulär polarisation (90° fasskillnad), sedan till elliptisk och så småningom linjär polarisation (180° fas) vinkelrät mot den ursprungliga polarisationen, sedan genom cirkulär igen (270) ° fas), sedan elliptisk med den ursprungliga azimutvinkeln, och slutligen tillbaka till det ursprungliga linjärt polariserade tillståndet (360 ° fas) där cykeln börjar på nytt. I allmänhet är situationen mer komplicerad och kan karakteriseras som en rotation i Poincaré-sfären kring den axel som definieras av utbredningssätten. Exempel på linjär (blå), cirkulär (röd) och elliptisk (gul) dubbelbrytning visas i figuren till vänster. Den totala intensiteten och graden av polarisation påverkas inte. Om väglängden i det dubbelbrytande mediet är tillräcklig kan de två polarisationskomponenterna i en kollimerad stråle (eller stråle ) lämna materialet med en positionsförskjutning, även om deras slutliga utbredningsriktningar kommer att vara desamma (förutsatt att ingångsytan och utgångsytan antas är parallella). Detta ses vanligtvis med hjälp av kalcitkristaller , som ger betraktaren två lätt förskjutna bilder, i motsatta polarisationer, av ett föremål bakom kristallen . Det var denna effekt som gav den första upptäckten av polarisering, av Erasmus Bartholinus 1669.

Dikroism

Medier där överföringen av ett polarisationsläge företrädesvis reduceras kallas dikroisk eller diattenuerande . Liksom dubbelbrytning kan diattenuering vara med avseende på linjära polarisationsmoder (i en kristall) eller cirkulära polarisationsmoder (vanligtvis i en vätska).

Enheter som blockerar nästan all strålning i ett läge kallas polariserande filter eller helt enkelt " polarisatorer ". Detta motsvarar g ₂ =0 i ovanstående representation av Jones-matrisen. Utsignalen från en ideal polarisator är ett specifikt polarisationstillstånd (vanligtvis linjär polarisation) med en amplitud lika med ingångsvågens ursprungliga amplitud i det polarisationsläget. Strömmen i det andra polarisationsläget är eliminerad. Således om opolariserat ljus leds genom en ideal polarisator (där g ₁ = 1 och g ₂ = 0) behålls exakt hälften av dess initiala effekt. Praktiska polarisatorer, speciellt billiga arkpolarisatorer, har ytterligare förluster så att g ₁ < 1. I många fall är emellertid den mer relevanta siffran polarisatorns grad av polarisation eller extinktionsförhållande, vilket involverar en jämförelse av g ₁ till g ₂ . Eftersom Jones-vektorer refererar till vågornas amplituder (snarare än intensitet ), när de belyses av opolariserat ljus kommer den återstående effekten i den oönskade polarisationen att vara ( g ₂ / g ₁ ) ² av effekten i den avsedda polarisationen.

Speglande reflektion

Förutom dubbelbrytning och dikroism i utökade medier, kan polarisationseffekter som kan beskrivas med Jones-matriser också inträffa vid (reflekterande) gränssnitt mellan två material med olika brytningsindex . Dessa effekter behandlas av Fresnel-ekvationerna . En del av vågen sänds ut och en del reflekteras; för ett givet material är dessa proportioner (och även reflektionsfasen) beroende av infallsvinkeln och är olika för s- och p -polarisationerna. Därför ändras i allmänhet polarisationstillståndet för reflekterat ljus (även om det initialt är opolariserat).

En bunt plattor i Brewsters vinkel mot en stråle reflekterar en bråkdel av det s -polariserade ljuset på varje yta och lämnar (efter många sådana plattor) en huvudsakligen p -polariserad stråle.

Allt ljus som träffar en yta med en speciell infallsvinkel känd som Brewsters vinkel , där reflektionskoefficienten för p- polarisation är noll, kommer att reflekteras med endast s -polarisationen kvar. Denna princip används i den så kallade "högen av plattor polarisatorn" (se figur) där en del av s -polarisationen avlägsnas genom reflektion vid varje Brewster-vinkelyta, vilket bara lämnar p- polarisationen efter överföring genom många sådana ytor. Den generellt sett mindre reflektionskoefficienten för p- polarisationen är också grunden för polariserade solglasögon ; genom att blockera s (horisontell) polarisering, avlägsnas det mesta av bländningen på grund av reflektion från till exempel en våt gata.

I det viktiga specialfallet med reflektion vid normal incidens (som inte involverar anisotropa material) finns det ingen speciell s- eller p- polarisation. Både x- och y- polarisationskomponenterna reflekteras identiskt, och därför är polariseringen av den reflekterade vågen identisk med den för den infallande vågen. Emellertid, i fallet med cirkulär (eller elliptisk) polarisation omkastas polarisationstillståndets handedness därigenom, eftersom detta enligt konventionen specificeras i förhållande till utbredningsriktningen. Den cirkulära rotationen av det elektriska fältet runt xy- axlarna som kallas "högerhänt" för en våg i +z -riktningen är "vänsterhänt" för en våg i -z- riktningen . Men i det allmänna fallet med reflektion vid en infallsvinkel som inte är noll, kan ingen sådan generalisering göras. Till exempel kommer höger-cirkulärt polariserat ljus som reflekteras från en dielektrisk yta i en betesvinkel fortfarande att vara högerhänt (men elliptiskt) polariserat. Linjärt polariserat ljus som reflekteras från en metall vid icke-normalt infall kommer i allmänhet att bli elliptiskt polariserat. Dessa fall hanteras med hjälp av Jones-vektorer som påverkas av de olika Fresnel-koefficienterna för s- och p -polarisationskomponenterna.

Mättekniker som involverar polarisering

Vissa optiska mättekniker är baserade på polarisering. I många andra optiska tekniker är polarisering avgörande eller måste åtminstone beaktas och kontrolleras; sådana exempel är för många för att nämnas.

Mätning av stress

Stress i plastglasögon

Inom ingenjörskonst möjliggör fenomenet spänningsinducerad dubbelbrytning att spänningar i transparenta material lätt kan observeras. Som noterats ovan och sett i det medföljande fotografiet, skapar kromaticiteten av dubbelbrytning typiskt färgade mönster när de ses mellan två polarisatorer. När yttre krafter appliceras observeras därigenom inre spänningar som induceras i materialet. Dessutom observeras dubbelbrytning ofta på grund av spänningar "infrusna" vid tillverkningstillfället. Detta är känt i cellofantejp vars dubbelbrytning beror på att materialet sträcker sig under tillverkningsprocessen.

Ellipsometri

Ellipsometri är en kraftfull teknik för att mäta de optiska egenskaperna hos en enhetlig yta. Det innebär att mäta ljusets polarisationstillstånd efter spegelreflektion från en sådan yta. Detta görs vanligtvis som en funktion av infallsvinkel eller våglängd (eller båda). Eftersom ellipsometri är beroende av reflektion krävs det inte att provet är transparent för ljus eller att dess baksida är tillgänglig.

Ellipsometri kan användas för att modellera det (komplexa) brytningsindexet för en yta av ett bulkmaterial. Det är också mycket användbart för att bestämma parametrar för ett eller flera tunna filmskikt avsatta på ett substrat. På grund av deras reflektionsegenskaper är inte bara den förutsagda magnituden av p- och s- polarisationskomponenterna, utan deras relativa fasförskjutningar vid reflektion, jämfört med mätningar med en ellipsometer. En normal ellipsometer mäter inte den faktiska reflektionskoefficienten (vilket kräver noggrann fotometrisk kalibrering av den lysande strålen) utan förhållandet mellan p- och s - reflektionerna, såväl som förändring av polarisationsellipticiteten (därav namnet) som induceras vid reflektion av ytan studerat. Förutom användning inom vetenskap och forskning, används ellipsometrar på plats för att styra till exempel produktionsprocesser.

Geologi

Mikrofotografi av ett vulkaniskt sandkorn ; Den övre bilden är planpolariserat ljus, den nedre bilden är korspolariserat ljus, skalrutan till vänster i mitten är 0,25 millimeter.

Egenskapen för (linjär) dubbelbrytning är utbredd i kristallina mineraler , och var verkligen avgörande i den första upptäckten av polarisering. Inom mineralogi utnyttjas denna egenskap ofta med hjälp av polarisationsmikroskop, i syfte att identifiera mineraler. Se optisk mineralogi för mer information.

Ljudvågor i fasta material uppvisar polarisering. Differentiell utbredning av de tre polarisationerna genom jorden är en avgörande faktor inom seismologiområdet . Horisontellt och vertikalt polariserade seismiska vågor ( skjuvvågor ) benämns SH och SV, medan vågor med longitudinell polarisation ( kompressionsvågor ) benämns P-vågor.

Kemi

Vi har sett (ovan) att dubbelbrytningen av en typ av kristall är användbar för att identifiera den, och därför är detektion av linjär dubbelbrytning särskilt användbar inom geologi och mineralogi . Linjärt polariserat ljus har i allmänhet sitt polariseringstillstånd ändrat vid överföring genom en sådan kristall, vilket gör att det sticker ut när det betraktas mellan två korsade polarisatorer, som ses på fotografiet ovan. På samma sätt, inom kemi, kan rotation av polarisationsaxlar i en flytande lösning vara ett användbart mått. I en vätska är linjär dubbelbrytning omöjlig, men det kan finnas cirkulär dubbelbrytning när en kiral molekyl är i lösning. När höger- och vänsterhänta enantiomerer av en sådan molekyl är närvarande i lika antal (en så kallad racemisk blandning) upphör deras effekter. Men när det bara finns en (eller en övervikt av en), som oftare är fallet för organiska molekyler , observeras en netto cirkulär dubbelbrytning (eller optisk aktivitet ), som avslöjar storleken på den obalansen (eller koncentrationen av molekylen) själv, när det kan antas att endast en enantiomer är närvarande). Detta mäts med hjälp av en polarimeter i vilken polariserat ljus leds genom ett rör av vätskan, i slutet av vilket är en annan polarisator som roteras för att nollställa överföringen av ljus genom den.

Astronomi

Inom många områden av astronomi är studiet av polariserad elektromagnetisk strålning från yttre rymden av stor betydelse. Även om det vanligtvis inte är en faktor i den termiska strålningen av stjärnor , är polarisering också närvarande i strålning från koherenta astronomiska källor (t.ex. hydroxyl- eller metanolmasrar ) , och osammanhängande källor som de stora radioloberna i aktiva galaxer och pulsarradiostrålning (som kan , det spekuleras, ibland vara koherent), och påtvingas också stjärnljus genom att spridas från interstellärt damm . Förutom att tillhandahålla information om strålningskällor och spridning, sonderar polarisation också det interstellära magnetfältet via Faraday-rotation . Polariseringen av den kosmiska mikrovågsbakgrunden används för att studera det mycket tidiga universums fysik. Synkrotronstrålning är i sig polariserad. Det har föreslagits att astronomiska källor orsakade chiraliteten hos biologiska molekyler på jorden.

Tillämpningar och exempel

Polariserade solglasögon

Effekt av en polarisator på reflektion från lera. På bilden till vänster överför den horisontellt orienterade polarisatorn företrädesvis dessa reflektioner; Att rotera polarisatorn 90° (höger) som man skulle se med polariserade solglasögon blockerar nästan allt spegelreflekterat solljus.

Man kan testa om solglasögon är polariserade genom att titta igenom två par, med det ena vinkelrätt mot det andra. Om båda är polariserade kommer allt ljus att blockeras.

Opolariserat ljus, efter att ha reflekterats av en spegelblank (blank) yta, erhåller i allmänhet en grad av polarisation. Detta fenomen observerades 1808 av matematikern Étienne-Louis Malus , efter vilken Malus lag är uppkallad. Polariserande solglasögon utnyttjar denna effekt för att reducera bländning från reflektioner från horisontella ytor, särskilt vägen framför betraktad i en betesvinkel.

Bärare av polariserade solglasögon kommer ibland att observera oavsiktliga polarisationseffekter såsom färgberoende dubbelbrytande effekter, till exempel i härdat glas (t.ex. bilfönster) eller föremål gjorda av transparent plast , i samband med naturlig polarisering genom reflektion eller spridning. Det polariserade ljuset från LCD-skärmar (se nedan) är mycket iögonfallande när dessa bärs.

Skypolarisering och fotografering

Effekterna av ett polariserande filter (höger bild) på himlen i ett fotografi

Polarisering observeras i ljuset av himlen , eftersom detta beror på solljus som sprids av aerosoler när det passerar genom jordens atmosfär . Det spridda ljuset producerar ljusstyrkan och färgen i klar himmel. Denna partiella polarisering av spritt ljus kan användas för att göra himlen mörkare i fotografier och öka kontrasten. Denna effekt observeras starkast vid punkter på himlen som gör en 90° vinkel mot solen. Polariserande filter använder dessa effekter för att optimera resultatet av fotografering av scener där reflektion eller spridning från himlen är inblandad.

Färgade fransar i Embassy Gardens Sky Pool när de ses genom en polarisator, på grund av stressinducerad dubbelbrytning i takfönstret

Skypolarisering har använts för orientering i navigering. Pfund himmelkompassen användes på 1950-talet när man navigerade nära polerna av jordens magnetfält när varken solen eller stjärnorna var synliga (t.ex. under dagtid moln eller skymning ). Det har föreslagits, kontroversiellt, att vikingarna utnyttjade en liknande anordning (" solstenen ") i sina omfattande expeditioner över Nordatlanten under 900-1100-talen, innan den magnetiska kompassen kom från Asien till Europa på 1100-talet . Besläktad med himmelkompassen är " polarklockan ", som uppfanns av Charles Wheatstone i slutet av 1800-talet.

Displayteknik

Principen för LCD- teknik (LCD) bygger på rotationen av den linjära polarisationsaxeln av den flytande kristalluppsättningen. Ljus från bakgrundsbelysningen (eller det bakre reflekterande lagret, i enheter som inte inkluderar eller kräver bakgrundsbelysning) passerar först genom ett linjärt polariserande ark. Det polariserade ljuset passerar genom själva flytande kristallskiktet som kan vara organiserat i pixlar (för en TV eller datorskärm) eller i ett annat format som en sjusegmentsskärm eller en med anpassade symboler för en viss produkt. Det flytande kristallskiktet produceras med en konsekvent höger- (eller vänster-) kiralitet, huvudsakligen bestående av små helixar . Detta orsakar cirkulär dubbelbrytning och är konstruerad så att det finns en 90 graders rotation av det linjära polarisationstillståndet. Men när en spänning appliceras över en cell, rätas molekylerna ut, vilket minskar eller helt förlorar den cirkulära dubbelbrytningen. På visningssidan av skärmen finns ett annat linjärt polariserande ark, vanligtvis orienterat 90 grader från det bakom det aktiva lagret. Därför, när den cirkulära dubbelbrytningen avlägsnas genom applicering av en tillräcklig spänning, förblir polariseringen av det transmitterade ljuset i rät vinkel mot den främre polarisatorn, och pixeln verkar mörk. Utan spänning gör dock 90 graders rotation av polarisationen att den exakt matchar den främre polarisatorns axel, vilket släpper igenom ljuset. Mellanspänningar skapar mellanliggande rotation av polarisationsaxeln och pixeln har en mellanliggande intensitet. Skärmar baserade på denna princip är utbredda och används nu i de allra flesta tv-apparater, datorskärmar och videoprojektorer, vilket gör den tidigare CRT -tekniken i princip föråldrad. Användningen av polarisering i driften av LCD-skärmar är omedelbart uppenbar för någon som bär polariserade solglasögon, vilket ofta gör skärmen oläslig.

I en helt annan mening har polarisationskodning blivit den ledande (men inte enda) metoden för att leverera separata bilder till vänster och höger öga i stereoskopiska skärmar som används för 3D-filmer . Detta innebär separata bilder avsedda för varje öga, antingen projicerade från två olika projektorer med ortogonalt orienterade polariserande filter eller, mer typiskt, från en enda projektor med tidsmultiplex polarisation (en snabb alternerande polarisationsanordning för successiva bildrutor). Polariserade 3D-glasögon med lämpliga polariserande filter ser till att varje öga endast får den avsedda bilden. Historiskt använde sådana system linjär polarisationskodning eftersom det var billigt och erbjöd bra separation. Cirkulär polarisering gör dock separationen av de två bilderna okänslig för lutning av huvudet, och används ofta i 3D-filmutställningar idag, som systemet från RealD . Att projicera sådana bilder kräver skärmar som bibehåller polariseringen av det projicerade ljuset när det ses i reflektion (såsom silverdukar) ; en normal diffus vit projektionsduk orsakar depolarisering av de projicerade bilderna, vilket gör den olämplig för denna applikation.

Även om de nu är föråldrade, led CRT-datorskärmar av reflektion från glashöljet, vilket orsakade bländning från rumsbelysning och följaktligen dålig kontrast. Flera antireflektionslösningar användes för att lindra detta problem. En lösning använde principen om reflektion av cirkulärt polariserat ljus. Ett cirkulärt polariserande filter framför skärmen möjliggör överföring av (säg) endast rätt cirkulärt polariserat rumsljus. Nu har rätt cirkulärt polariserat ljus (beroende på vilken konvention som används) sin elektriska (och magnetiska) fältriktning roterande medurs medan den fortplantar sig i +z-riktningen. Vid reflektion har fältet fortfarande samma rotationsriktning, men nu är utbredningen i −z-riktningen vilket gör att den reflekterade vågen lämnas cirkulärt polariserad. Med det högra cirkulära polarisationsfiltret placerat framför det reflekterande glaset, kommer det oönskade ljuset som reflekteras från glaset således att vara i mycket polarisationstillstånd som blockeras av det filtret, vilket eliminerar reflektionsproblemet. Omkastningen av cirkulär polarisation vid reflektion och eliminering av reflektioner på detta sätt kan lätt observeras genom att titta i en spegel medan du bär 3D-filmglasögon som använder vänster- och högerhänt cirkulär polarisering i de två linserna. Om man stänger ett öga kommer det andra ögat att se en reflektion där det inte kan se sig själv; linsen ser svart ut. Den andra linsen (av det slutna ögat) kommer dock att ha den korrekta cirkulära polariseringen vilket gör att det slutna ögat lätt kan ses av det öppna.

Radiosändning och mottagning

Alla radio- (och mikrovågs) antenner som används för att sända eller ta emot är polariserade i sig. De sänder in (eller tar emot signaler från) en viss polarisation, och är totalt okänsliga för den motsatta polariseringen; i vissa fall är polarisering en funktion av riktning. De flesta antenner är nominellt linjärt polariserade, men elliptisk och cirkulär polarisering är en möjlighet. Såsom är konventionen inom optik, förstås "polariseringen" av en radiovåg att hänvisa till polariseringen av dess elektriska fält, med magnetfältet i en 90 graders rotation med avseende på det för en linjärt polariserad våg.

De allra flesta antenner är linjärt polariserade. I själva verket kan det visas från symmetriöverväganden att en antenn som ligger helt i ett plan som även inkluderar observatören, endast kan ha sin polarisering i riktning mot det planet. Detta gäller i många fall, vilket gör att man enkelt kan sluta sig till en sådan antenns polarisation i en avsedd utbredningsriktning. Så en typisk Yagi -antenn på taket eller log-periodisk antenn med horisontella ledare, sett från en andra station mot horisonten, är nödvändigtvis horisontellt polariserad. Men en vertikal " piskantenn " eller AM-sändningstorn som används som ett antennelement (återigen, för observatörer som är horisontellt förskjutna från det) kommer att sända i den vertikala polarisationen. En vändkorsantenn med sina fyra armar i horisontalplanet sänder likaså horisontellt polariserad strålning mot horisonten. Men när samma vändkorsantenn används i "axiellt läge" (uppåt, för samma horisontellt orienterade struktur) är dess strålning cirkulärt polariserad. På mellanliggande höjder är den elliptiskt polariserad.

Polarisering är viktig i radiokommunikation eftersom, till exempel, om man försöker använda en horisontellt polariserad antenn för att ta emot en vertikalt polariserad sändning, kommer signalstyrkan att reduceras avsevärt (eller under mycket kontrollerade förhållanden, reduceras till ingenting). Denna princip används i satellit-tv för att fördubbla kanalkapaciteten över ett fast frekvensband. Samma frekvenskanal kan användas för två signaler som sänds i motsatta polarisationer. Genom att justera mottagningsantennen för den ena eller andra polarisationen kan endera signalen väljas utan störningar från den andra.

Speciellt på grund av närvaron av marken finns det vissa skillnader i utbredning (och även i reflektioner som är ansvariga för TV- spökbilder ) mellan horisontella och vertikala polariseringar. AM- och FM-radio använder vanligtvis vertikal polarisering, medan TV använder horisontell polarisering. Speciellt vid låga frekvenser undviks horisontell polarisering. Det beror på att fasen för en horisontellt polariserad våg omkastas vid reflektion från marken. En avlägsen station i horisontell riktning kommer att ta emot både den direkta och reflekterade vågen, som därmed tenderar att ta emot varandra. Detta problem undviks med vertikal polarisering. Polarisering är också viktig vid sändning av radarpulser och mottagning av radarreflektioner av samma eller en annan antenn. Till exempel kan bakåtspridning av radarpulser genom regndroppar undvikas genom att använda cirkulär polarisering. Precis som spegelreflektion av cirkulärt polariserat ljus vänder polarisationens handenhet, som diskuterats ovan, gäller samma princip för spridning av föremål som är mycket mindre än en våglängd, såsom regndroppar. Å andra sidan kommer reflektion av den vågen av ett oregelbundet metallföremål (såsom ett flygplan) typiskt att introducera en förändring i polarisation och (partiell) mottagning av returvågen av samma antenn.

Effekten av fria elektroner i jonosfären , i samband med jordens magnetfält , orsakar Faraday-rotation , en sorts cirkulär dubbelbrytning. Detta är samma mekanism som kan rotera axeln för linjär polarisering av elektroner i det interstellära rymden som nämns nedan . Storleken på Faraday-rotationen som orsakas av en sådan plasma är kraftigt överdriven vid lägre frekvenser, så vid de högre mikrovågsfrekvenserna som används av satelliter är effekten minimal. påverkas medel- eller kortvågsöverföringar som tas emot efter brytning av jonosfären starkt. Eftersom en vågs väg genom jonosfären och jordens magnetfältsvektor längs en sådan väg är ganska oförutsägbara, kommer en våg som sänds med vertikal (eller horisontell) polarisation i allmänhet att ha en resulterande polarisation i en godtycklig orientering vid mottagaren.

Cirkulär polarisering genom ett flygplans plastfönster, 1989

Polarisering och vision

Många djur är kapabla att uppfatta några av komponenterna i polarisationen av ljus, t.ex. linjärt horisontellt polariserat ljus. Detta används vanligtvis för navigeringsändamål, eftersom den linjära polariseringen av himmelljus alltid är vinkelrät mot solens riktning. Denna förmåga är mycket vanlig bland insekter , inklusive bin , som använder denna information för att orientera sina kommunikativa danser . Polarisationskänslighet har också observerats hos arter av bläckfisk , bläckfisk , bläckfisk och mantisräkor . I det senare fallet mäter en art alla sex ortogonala polarisationskomponenter och tros ha optimal polarisationsseende. De snabbt föränderliga, livligt färgade hudmönstren hos bläckfisk, som används för kommunikation, innehåller också polarisationsmönster, och mantisräkor är kända för att ha polarisationsselektiv reflekterande vävnad. Skypolarisering ansågs uppfattas av duvor , vilket antogs vara ett av deras hjälpmedel vid målsökning , men forskning visar att detta är en populär myt.

Det blotta mänskliga ögat är svagt känsligt för polarisering, utan behov av mellanliggande filter. Polariserat ljus skapar ett mycket svagt mönster nära mitten av synfältet, kallat Haidingers borste . Detta mönster är mycket svårt att se, men med övning kan man lära sig att upptäcka polariserat ljus med blotta ögat.

Vinkelmoment med cirkulär polarisation

Det är välkänt att elektromagnetisk strålning bär ett visst linjärt momentum i utbredningsriktningen. Dessutom bär ljuset dock ett visst vinkelmoment om det är cirkulärt polariserat (eller delvis). I jämförelse med lägre frekvenser som mikrovågor är mängden vinkelmoment i ljus , även av ren cirkulär polarisation, jämfört med samma vågs linjära rörelsemängd (eller strålningstryck ) mycket liten och svår att ens mäta. Den användes dock i ett experiment för att uppnå hastigheter på upp till 600 miljoner varv per minut.

Se även

Citerade referenser

Allmänna referenser

Principles of Optics , 7:e upplagan, M. Born & E. Wolf, Cambridge University, 1999, ISBN 0-521-64222-1 .
Fundamentals of polarized light: a statistical optics approach , C. Brosseau, Wiley, 1998, ISBN 0-471-14302-2 .
Polarized Light, andra upplagan , Dennis Goldstein, Marcel Dekker, 2003, ISBN 0-8247-4053-X .
Field Guide to Polarization , Edward Collett, SPIE Field Guides vol. FG05 , SPIE, 2005, ISBN 0-8194-5868-6 .
Polarization Optics in Telecommunications , Jay N. Damask, Springer 2004, ISBN 0-387-22493-9 .
Polarized Light in Nature , GP Können, Översatt av GA Beerling, Cambridge University, 1985, ISBN 0-521-25862-6 .
Polarized Light in Science and Nature , D. Pye , Institute of Physics, 2001, ISBN 0-7503-0673-4 .
Polariserat ljus, produktion och användning , William A. Shurcliff, Harvard University, 1962.
Ellipsometri och polariserat ljus , RMA Azzam och NM Bashara, North-Holland, 1977, ISBN 0-444-87016-4 .
Secrets of the Viking Navigators – Hur vikingarna använde sina fantastiska solstenar och andra tekniker för att korsa de öppna haven , Leif Karlsen, One Earth Press, 2003.

externa länkar

Feynmans föreläsning om polarisering
Polariserat ljus i naturen och tekniken
Digitalt bildgalleri med polariserat ljus : Mikroskopiska bilder gjorda med polarisationseffekter
Polarisering av University of Colorado Physics 2000 : Animerad förklaring av polarisering
MathPages: Förhållandet mellan fotonspin och polarisering
Ett virtuellt polarisationsmikroskop
Polarisationsvinkel i parabolantenner .
Använda polarisatorer i fotografering
Molecular Expressions: Science, Optics and You — Polarization of Light : Interactive Java-tutorial
SPIE teknisk grupp för polarisering
Antennpolarisering
Animationer av linjära, cirkulära och elliptiska polarisationer på YouTube