Rotsystem

Den här artikeln handlar om rotsystem i matematik. För växtrotsystem , se Rot .

I matematik är ett rotsystem en konfiguration av vektorer i ett euklidiskt utrymme som uppfyller vissa geometriska egenskaper. Konceptet är grundläggande i teorin om Lie-grupper och Lie-algebror , särskilt klassificerings- och representationsteorin för semisimpla Lie-algebror . Eftersom Lie-grupper (och vissa analoger som algebraiska grupper ) och Lie-algebror har blivit viktiga i många delar av matematiken under nittonhundratalet, motsäger rotsystemens till synes speciella karaktär antalet områden där de tillämpas. Vidare förekommer klassificeringsschemat för rotsystem, enligt Dynkin-diagram , i delar av matematiken utan någon öppen koppling till Lie-teorin (som singularitetsteorin) . Slutligen är rotsystem viktiga för sin egen skull, som i spektralgrafteorin .

Definitioner och exempel

De sex vektorerna i rotsystemet A ₂

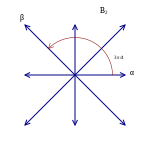
Som ett första exempel, betrakta de sex vektorerna i det 2-dimensionella euklidiska rummet , R ² , som visas i bilden till höger; kalla dem rötter . Dessa vektorer spänner över hela utrymmet. Om du betraktar linjen vinkelrät mot någon rot, säg β , så skickar reflektionen av R ² i den linjen vilken annan rot som helst, säg α , till en annan rot. Dessutom är roten till vilken den skickas lika med α + nβ , där n är ett heltal (i detta fall är n lika med 1). Dessa sex vektorer uppfyller följande definition och bildar därför ett rotsystem; denna är känd som A ₂ .

Definition

Låt E vara ett ändligt dimensionellt euklidiskt vektorrum , med den euklidiska standardinre produkten betecknad med $(\cdot ,\cdot )$ . Ett rotsystem $\Phi$ i E är en ändlig uppsättning vektorer som inte är noll (kallade rötter ) som uppfyller följande villkor:

1. Rötterna spänner över E .
2. De enda skalära multiplerna av en rot $\alpha \in \Phi$ som hör till $\Phi$ är själva $\alpha$ och $-\alpha$ .
3. För varje rot $\alpha \in \Phi$ stängs mängden ${\displaystyle \Phi } under$ reflektion genom hyperplanet vinkelrätt mot $\alpha$ .
4. ( Integralitet ) Om $\alpha$ och $\beta$ är rötter i $\Phi$ , då projektionen av $\beta$ på linjen genom $\ alpha$ är ett heltal eller halvheltalsmultipel av $\alpha$ .

Ett likvärdigt sätt att skriva villkor 3 och 4 är följande:

3. För två valfria rötter $\alpha ,\beta \in \Phi$ , innehåller mängden $\Phi$ elementet $\sigma _{\alpha }(\beta ):=\beta -2{\frac {(\alpha ,\beta )}{(\alpha ,\alpha )}}\alpha .$
4. För två valfria rötter $\alpha ,\beta \in \Phi$ , talet $\langle \beta ,\alpha \rangle :=2{\frac {(\alpha ,\beta )}{(\alpha ,\alpha )}}$ är ett heltal .

Vissa författare inkluderar endast villkor 1–3 i definitionen av ett rotsystem. I detta sammanhang kallas ett rotsystem som också uppfyller integralitetsvillkoret ett kristallografiskt rotsystem . Andra författare utelämnar villkor 2; sedan kallar de rotsystem som uppfyller villkor 2 reducerat . I den här artikeln antas alla rotsystem vara reducerade och kristallografiska.

Med tanke på egenskap 3 är integralitetsvillkoret ekvivalent med att ange att β och dess reflektion σ _α ( β ) skiljer sig åt med en heltalsmultipel av α . Observera att operatören

$$\langle \cdot ,\cdot \rangle \colon \Phi \times \Phi \to \mathbb {Z}$$

definierad av egenskap 4 är inte en inre produkt. Det är inte nödvändigtvis symmetriskt och är linjärt endast i det första argumentet.

Rank-2 rotsystem

Rotsystem $A_{1}\times A_{1}$	Rotsystem $D_{2}$
Rotsystem $A_{2}$	Rotsystem $G_{2}$
Rotsystem $B_{2}$	Rotsystem $C_{2}$

Rangen för ett rotsystem Φ är dimensionen av E . Två rotsystem kan kombineras genom att betrakta de euklidiska utrymmena som de sträcker sig över som ömsesidigt ortogonala underrum till ett gemensamt euklidiskt utrymme. Ett rotsystem som inte härrör från en sådan kombination, såsom systemen A ₂ , B ₂ , och G ₂ som visas till höger, sägs vara irreducerbart .

Två rotsystem ( E ₁ , Φ ₁ ) och ( E ₂ , Φ ₂ ) kallas isomorfa om det finns en inverterbar linjär transformation E ₁ → E ₂ som skickar Φ ₁ till Φ ₂ så att för varje par av rötter, talet $\langle x,y\rangle$ bevaras.

Rotnätet i ett rotsystem Φ är Z -submodulen av E som genereras av Φ. Det är ett galler i E .

Weyl-gruppen

Huvudartikel: Weyl group

Weylgruppen i $A_{2}$ rotsystemet är symmetrigruppen i en liksidig triangel

Gruppen av isometrier av E som genereras av reflektioner genom hyperplan associerade med rötter av Φ kallas Weyl - gruppen av Φ. Eftersom den verkar troget på den finita mängden Φ är Weyl-gruppen alltid finit. Reflexionsplanen är hyperplanen vinkelräta mot rötterna, indikerade för $A_{2}$ med streckade linjer i figuren nedan. Weyl-gruppen är symmetrigruppen i en liksidig triangel, som har sex element. I det här fallet är Weyl-gruppen inte den fullständiga symmetrigruppen i rotsystemet (t.ex. en 60-graders rotation är en symmetri av rotsystemet men inte ett element i Weyl-gruppen).

Rangordna ett exempel

Det finns bara ett rotsystem av rang 1, bestående av två vektorer som inte är noll $\{\alpha ,-\alpha \}$ . Detta rotsystem kallas $A_{1}$ .

Rangordna två exempel

I rang 2 finns fyra möjligheter, motsvarande $\sigma _{\alpha }(\beta )=\beta +n\alpha$ , där $n=0,1,2,3$ . Figuren till höger visar dessa möjligheter, men med några redundanser: $A_{1}\ gånger A_{1}$ är isomorf till $D_{2}$ och ${\ displaystyle B_{2}}$ är isomorf till $C_{2}$ .

Observera att ett rotsystem inte bestäms av det gitter som det genererar: $A_{1}\times A_{1}$ och $B_{2}$ genererar båda ett kvadratiskt gitter medan $A_{2}$ och $G_{2}$ båda genererar ett hexagonalt gitter .

Närhelst Φ är ett rotsystem i E , och S är ett delrum av E som sträcks av Ψ = Φ ∩ S , då är Ψ ett rotsystem i S . Således visar den uttömmande listan av fyra rotsystem av rang 2 de geometriska möjligheterna för vilka två rötter som helst, valda från ett rotsystem av godtycklig rang. I synnerhet måste två sådana rötter mötas i en vinkel på 0, 30, 45, 60, 90, 120, 135, 150 eller 180 grader.

Rotsystem som härrör från halvenkla Lie-algebror

Se även: Semienkel Lie-algebra § Cartan-subalgebra och rotsystem , och Rotsystemet för en semi-enkel Lie-algebra

Om ${\mathfrak {g}}$ är en komplex halvenkel Lie-algebra och ${\mathfrak {h}}$ är en kartansk subalgebra , kan vi konstruera ett rotsystem enligt följande. Vi säger att $\alpha \in {\mathfrak {h}}^{*}$ är en rot av ${\mathfrak {g}}$ relativt ${\ mathfrak {h}}$ om $\alpha \neq 0$ och det finns något $X\neq 0\i {\mathfrak {g}}$ så att

$$[H,X]=\alpha (H)X$$

för alla $H\in {\mathfrak {h}}$ . Man kan visa att det finns en inre produkt för vilken uppsättningen rötter bildar ett rotsystem. Rotsystemet för ${\mathfrak {g}}$ är ett grundläggande verktyg för att analysera strukturen för ${\mathfrak {g}}$ och klassificera dess representationer. (Se avsnittet nedan om rotsystem och lögnteori.)

Historia

Begreppet rotsystem introducerades ursprungligen av Wilhelm Killing omkring 1889 (på tyska, Wurzelsystem ). Han använde dem i sitt försök att klassificera alla enkla Lie algebror över området komplexa tal . Killing gjorde ursprungligen ett misstag i klassificeringen och listade två exceptionella rotsystem i rang 4, när det i själva verket bara finns ett, nu känt som F ₄ . Cartan korrigerade senare detta misstag genom att visa Killings två rotsystem var isomorfa.

Killing undersökte strukturen hos en Lie-algebra $L$ , genom att betrakta vad som nu kallas en Cartan-subalgebra ${\mathfrak {h}}$ . Sedan studerade han rötterna till det karakteristiska polynomet ${\displaystyle \det(\operatörsnamn {ad} _{L}xt)} ,$ där $x\in {\mathfrak {h}}$ . Här betraktas en rot som en funktion av ${\mathfrak {h}}$ , eller faktiskt som ett element i det dubbla vektorutrymmet ${\mathfrak {h}}^{*}$ . Denna uppsättning rötter bildar ett rotsystem inuti ${\displaystyle {\mathfrak {h}}^{*}} ,$ som definierats ovan, där den inre produkten är Killing-formen .

Elementära konsekvenser av rotsystemets axiom

Integralitetsvillkoret för $\langle \beta ,\alpha \rangle$ uppfylls endast för β på en av de vertikala linjerna, medan integralitetsvillkoret för $\langle \ alpha ,\beta \rangle$ uppfylls endast för β på en av de röda cirklarna. Varje β vinkelrätt mot α (på Y -axeln) uppfyller trivialt båda med 0, men definierar inte ett irreducerbart rotsystem. Moduloreflektion, för en given α finns det bara 5 icke-triviala möjligheter för β , och 3 möjliga vinklar mellan α och β i en uppsättning enkla rötter. Nedsänkta bokstäver motsvarar serien av rotsystem för vilka den givna β kan fungera som den första roten och α som den andra roten (eller i F ₄ som de mittersta 2 rötterna).

Cosinus för vinkeln mellan två rötter är begränsad till att vara hälften av kvadratroten ur ett positivt heltal. Detta beror på att $\langle \beta ,\alpha \rangle$ och $\langle \alpha ,\beta \rangle$ båda är heltal, enligt antagande, och

$${\begin{aligned}\langle \beta ,\alpha \rangle \langle \alpha ,\beta \rangle &=2{\frac {(\alpha ,\beta )}{(\alpha ,\alpha ) }}\cdot 2{\frac {(\alpha ,\beta )}{(\beta ,\beta )}}\\&=4{\frac {(\alpha ,\beta )^{2}}{\ vert \alpha \vert ^{2}\vert \beta \vert ^{2}}}\\&=4\cos ^{2}(\theta )=(2\cos(\theta ))^{2} \in \mathbb {Z} .\end{aligned}}$$

Eftersom ${\displaystyle 2\cos(\theta )\in [-2,2]} är$ de enda möjliga värdena för $\cos( \theta )$$\displaystyle 0,\pm {\tfrac {1}{2}},\pm {\tfrac {\sqrt {2}}{2} },\pm {\tfrac {\sqrt {3}}{2}}}$ ± och $\pm {\tfrac {\sqrt {4}}{2}}=\pm 1$ , motsvarande vinklar på 90°, 60° eller 120°, 45° eller 135°, 30° eller 150° och 0° eller 180°. Villkor 2 säger att inga skalära multipler av α förutom 1 och −1 kan vara rötter, så 0 eller 180°, vilket skulle motsvara 2 α eller −2 α , är ute. Diagrammet till höger visar att en vinkel på 60° eller 120° motsvarar lika långa rötter, medan en vinkel på 45° eller 135° motsvarar ett längdförhållande på 2 {\displaystyle {\sqrt {2}} $och$ en vinkel på 30° eller 150° motsvarar ett längdförhållande på ${\sqrt {3}}$ .

Sammanfattningsvis, här är de enda möjligheterna för varje par av rötter.

• vinkel på 90 grader; i så fall är längdförhållandet obegränsat.
• Vinkel på 60 eller 120 grader, med ett längdförhållande på 1.
• Vinkel på 45 eller 135 grader, med ett längdförhållande på ${\sqrt {2}}$ .
• Vinkel på 30 eller 150 grader, med ett längdförhållande på ${\sqrt {3}}$ .

Positiva rötter och enkla rötter

De märkta rötterna är en uppsättning positiva rötter för $G_{2}$ rotsystemet, med $\alpha _{1}$ och $\alpha _{2}$ vara de enkla rötterna

Givet ett rotsystem $\Phi$ kan vi alltid välja (på många sätt) en uppsättning positiva rötter . Detta är en delmängd $\Phi ^{+}$ av $\Phi$ så att

• För varje rot ${\displaystyle \alpha \in \Phi } finns$ exakt en av rötterna $\alpha$ , $-\alpha$ i $\Phi ^{ +}$ .
• För två distinkta $\alpha ,\beta \in \Phi ^{+}$ så att $\alpha +\beta$ är en rot, $\alpha +\beta \in \Phi ^{+}$ .

Om en uppsättning positiva rötter $\Phi ^{+}$ väljs, kallas element av $-\Phi ^{+}$ negativa rötter . En uppsättning positiva rötter kan konstrueras genom att välja ett hyperplan $V$ som inte innehåller någon rot och sätta $\Phi ^{+}$ för att vara alla rötter som ligger på en fast sida av ${\ displaystil V}$ . Dessutom uppstår varje uppsättning positiva rötter på detta sätt.

Ett element av $\Phi ^{+}$ kallas en enkel rot (även fundamental rot ) om det inte kan skrivas som summan av två element av $\Phi ^{+}$ . (Mängden enkla rötter hänvisas också till som en bas för $\Phi$ .) Mängden $\Delta$ av enkla rötter är en bas för $E$ med följande extra specialitet egenskaper:

• Varje rot $\alpha \in \Phi$ är en linjär kombination av element i $\Delta$ med heltalskoefficienter .
• För varje ${\displaystyle \alpha \in \Phi } ,$ är koefficienterna i föregående punkt antingen alla icke-negativa eller alla icke-positiva.

För varje rotsystem $\Phi$ finns det många olika val av uppsättningen positiva rötter – eller, på motsvarande sätt, av de enkla rötter – men vilka två uppsättningar positiva rötter som helst skiljer sig åt genom verkan av Weyl-gruppen.

Dubbla rotsystem, rotor och integrerade element

Se även: Langlands dubbelgrupp

Det dubbla rotsystemet

Om Φ är ett rotsystem i E definieras koroten α ∨ av en rot α ^av

$$\alpha ^{\vee }={2 \over (\alpha ,\alpha )}\,\alpha .$$

Uppsättningen av rotor bildar också ett rotsystem Φ ^∨ i E , som kallas det dubbla rotsystemet (eller ibland omvänt rotsystem ). Per definition är α ^{∨ ∨} = α, så att Φ är det dubbla rotsystemet för Φ ^∨ . Gittret i E som spänner över av Φ ^∨ kallas för korotsgittret . Både Φ och Φ ^∨ har samma Weyl-grupp W och, för s i W ,

$$(s\alpha )^{\vee }=s(\alpha ^{\vee }).$$

Om Δ är en uppsättning enkla rötter för Φ, så är Δ ^∨ en uppsättning enkla rötter för Φ ^∨ .

I klassificeringen som beskrivs nedan, rotsystemen av typ $A_{n}$ och $D_{n}$ tillsammans med de exceptionella rotsystemen $E_{6},E_{7},E_{8},F_{4},G_{2}$ är alla självduala, vilket betyder att det dubbla rotsystemet är isomorft till det ursprungliga rotsystemet. Däremot $B_{n}$ och $C_{n}$ dubbla till varandra, men inte isomorfa (förutom när $n=2$ ) .

Integrerade element

Se även: Vikt (representationsteori) § Vikter i representationsteorin för semisimple Lie-algebror

En vektor $\lambda$ i E kallas integral om dess inre produkt med varje korot är ett heltal:

$$2{\frac {(\lambda ,\alpha )}{(\alpha ,\alpha )}}\in \mathbb {Z} ,\quad \alpha \in \Phi .$$

Eftersom mängden $\alpha ^{\vee }$ med $\alpha \in \Delta$ bildar en bas för det dubbla rotsystemet, för att verifiera att $\lambda$ är integral, räcker det att kontrollera ovanstående villkor för $\alpha \in \Delta$ .

Uppsättningen av integrerade element kallas viktgittret som är associerat med det givna rotsystemet. Denna term kommer från representationsteorin för semisimpla Lie-algebras , där integralelementen bildar möjliga vikter av finita dimensionella representationer.

Definitionen av ett rotsystem garanterar att själva rötterna är integrerade element. Således är varje heltals linjär kombination av rötter också integral. I de flesta fall kommer det dock att finnas integralelement som inte är heltalskombinationer av rötter. Det vill säga i allmänhet sammanfaller inte viktgittret med rotgittret.

Klassificering av rotsystem med Dynkin-diagram

Se även: Dynkin-diagram

Bilder på alla anslutna Dynkin-diagram

Ett rotsystem är irreducerbart om det inte kan delas in i föreningen av två korrekta delmängder ${\displaystyle \Phi =\Phi _{1}\cup \Phi _{2}} ,$ så att $(\alpha ,\beta )=0$ för alla $\alpha \in \Phi _{1}$ och $\beta \in \ Phi _{2}$ .

Irreducerbara rotsystem motsvarar vissa grafer , Dynkin-diagrammen uppkallade efter Eugene Dynkin . Klassificeringen av dessa grafer är en enkel fråga om kombinatorik och inducerar en klassificering av irreducerbara rotsystem.

Konstruera Dynkin-diagrammet

Med tanke på ett rotsystem, välj en uppsättning Δ av enkla rötter som i föregående avsnitt. Hörnen i det tillhörande Dynkin-diagrammet motsvarar rötterna i Δ. Kanter ritas mellan hörn enligt följande, enligt vinklarna. (Observera att vinkeln mellan enkla rötter alltid är minst 90 grader.)

• Ingen kant om vektorerna är ortogonala,
• En oriktad enkelkant om de bildar en vinkel på 120 grader,
• En riktad dubbelkant om de gör en vinkel på 135 grader, och
• En riktad trippelkant om de gör en vinkel på 150 grader.

Termen "riktad kant" betyder att dubbla och trippelkanter är markerade med en pil som pekar mot den kortare vektorn. (Att tänka på pilen som ett "större än"-tecken gör det tydligt åt vilket håll pilen är tänkt att peka.)

Observera att av de elementära egenskaperna hos rötter som noterats ovan kan reglerna för att skapa Dynkin-diagrammet också beskrivas enligt följande. Ingen kant om rötterna är ortogonala; för icke-ortogonala rötter, en enkel-, dubbel- eller trippelkant beroende på om längdförhållandet mellan den längre och kortare är 1, ${\sqrt {2}}$ , ${\sqrt {3}}$ . I fallet med $G_{2}$ till exempel, finns det två enkla rötter i en vinkel på 150 grader (med ett längdförhållande på ${\sqrt {3}}$ ) . Således har Dynkin-diagrammet två hörn sammanfogade av en trippelkant, med en pil som pekar från vertexet som är associerat med den längre roten till den andra vertexen. (I det här fallet är pilen lite överflödig, eftersom diagrammet är likvärdigt var pilen än går.)

Klassificering av rotsystem

Även om ett givet rotsystem har mer än en möjlig uppsättning enkla rötter, agerar Weyl-gruppen transitivt på sådana val. Följaktligen är Dynkin-diagrammet oberoende av valet av enkla rötter; det bestäms av själva rotsystemet. Omvänt, givet två rotsystem med samma Dynkin-diagram, kan man matcha rötter, börja med rötterna i basen, och visa att systemen i själva verket är desamma.

Således minskar problemet med att klassificera rotsystem till problemet med att klassificera möjliga Dynkin-diagram. Ett rotsystem är irreducerbart om och endast om dess Dynkin-diagram är anslutna. De möjliga anslutna diagrammen är som visas i figuren. De nedsänkta anger antalet hörn i diagrammet (och därav rankningen av motsvarande irreducerbara rotsystem).

Om ${\displaystyle \Phi } är ett rotsystem,$ erhålls Dynkin-diagrammet för det dubbla rotsystemet ${\displaystyle \Phi ^{\vee }} från Dynkin-diagrammet för$$\Phi$ genom att behålla alla samma hörn och kanter, men omvända riktningarna för alla pilar. Således kan vi se från deras Dynkin-diagram att $B_{n}$ och $C_{n}$ är dubbla till varandra.

Weyl-kammare och Weyl-gruppen

Se även: Coxeter-grupp § Affine Coxeter-grupper

Det skuggade området är den grundläggande Weyl-kammaren för basen $\{\alpha _{1},\alpha _{2}\}$

Om $\Phi \subset E$ är ett rotsystem, kan vi betrakta hyperplanet vinkelrätt mot varje rot $\alpha$ . Kom ihåg att $\sigma _{\alpha }$ betecknar reflektionen kring hyperplanet och att Weyl-gruppen är gruppen av transformationer av $E$ som genereras av alla $\sigma _ {\alpha }$ s. Komplementet av uppsättningen hyperplan kopplas bort, och varje ansluten komponent kallas en Weyl-kammare . Om vi ​​har fixerat en viss uppsättning Δ av enkla rötter, kan vi definiera den $( \alpha ,v)>0$ Weyl-kammaren som är associerad med Δ som uppsättningen av punkter $v\in E$ så att för alla $\alpha \in \Delta$ .

Eftersom reflektionerna $\sigma _{\alpha },\,\alpha \in \Phi$ bevarar $\Phi$ , bevarar de också uppsättningen av hyperplan vinkelräta mot rötterna. Således permuterar varje Weyl-gruppelement Weyl-kamrarna.

Figuren illustrerar fallet med $A_{2}$ rotsystem. "Hyperplanen" (i detta fall endimensionella) ortogonala mot rötterna indikeras med streckade linjer. De sex 60-graderssektorerna är Weyl-kamrarna och den skuggade regionen är den grundläggande Weyl-kammaren som är associerad med den angivna basen.

En grundläggande allmän sats om Weyl-kammare är detta:

Sats : Weyl-gruppen verkar fritt och transitivt på Weyl-kamrarna. Således är ordningen för Weyl-gruppen lika med antalet Weyl-kammare.

I fallet $A_{2}$ , till exempel, har Weyl-gruppen sex element och det finns sex Weyl-kammare.

Ett relaterat resultat är detta:

Sats : Fixa en Weyl-kammare $C$ . Sedan för alla ${\displaystyle v\in E} innehåller$ Weyl-banan för $v$ exakt en punkt i stängningen ${\bar {C}}$ av ${\ displaystil C}$ .

Rotsystem och lögnteori

Irreducerbara rotsystem klassificerar ett antal relaterade objekt i Lie-teorin, särskilt följande:

• enkla komplexa Lie-algebror (se diskussionen ovan om rotsystem som härrör från halvenkla Lie-algebror),
• enkelt sammankopplade komplexa Lie-grupper som är enkla modulocentra, och
• enkelt sammankopplade kompakta Lie-grupper som är enkla modulocenter.

I varje fall är rötterna vikter som inte är noll för den adjoint representationen .

Vi ger nu en kort indikation på hur irreducibla rotsystem klassificerar enkla Lie-algebror över ${\displaystyle \mathbb {C} } ,$ efter argumenten i Humphreys. Ett preliminärt resultat säger att en semisenkel Lie-algebra är enkel om och endast om det associerade rotsystemet är irreducerbart. Vi begränsar därför uppmärksamheten till irreducerbara rotsystem och enkla Lie-algebror.

• Först måste vi fastställa att för varje enkel algebra ${\mathfrak {g}}$ finns det bara ett rotsystem. Detta påstående följer av resultatet att Cartan-subalgebra av ${\mathfrak {g}}$ är unik upp till automorfism, av vilket det följer att två godtyckliga Cartan-subalgebra ger isomorfa rotsystem.
• Därefter måste vi visa att för varje irreducerbart rotsystem kan det finnas högst en Lie-algebra, det vill säga att rotsystemet bestämmer Lie-algebra upp till isomorfism.
• Slutligen måste vi visa att det för varje irreducerbart rotsystem finns en associerad enkel Lie-algebra. Detta påstående är uppenbart för rotsystemen av typ A, B, C och D, för vilka de associerade Lie-algebrorna är de klassiska Lie-algebrorna . Det är sedan möjligt att analysera de exceptionella algebrorna från fall till fall. Alternativt kan man utveckla en systematisk procedur för att bygga en Lie-algebra från ett rotsystem, med hjälp av Serres relationer .

För kopplingar mellan de exceptionella rotsystemen och deras Lie-grupper och Lie-algebror, se E ₈ , E ₇ , E ₆ , F ₄ , och G ₂ .

Egenskaper hos de irreducerbara rotsystemen

$\Phi$	$|\Phi |$	$|\Phi ^{<}|$	jag	D	$|W|$
A n ( n ≥ 1)	n ( n + 1)			n + 1	( n + 1)!
B n ( n ≥ 2)	2 n 2	2 n	2	2	2 n n !
C n ( n ≥ 3)	2 n 2	2 n ( n − 1)	2 n −1	2	2 n n !
D n ( n ≥ 4)	2 n ( n − 1)			4	2 n −1 n !
E 6	72			3	51840
E 7	126			2	2903040
E 8	240			1	696729600
F 4	48	24	4	1	1152
G 2	12	6	3	1	12

Irreducerbara rotsystem namnges enligt deras motsvarande anslutna Dynkin-diagram. Det finns fyra oändliga familjer (A _n , B _n , C _n och D _n , kallade de klassiska rotsystemen ) och fem undantagsfall (de exceptionella rotsystemen ). Subskriptet anger rotsystemets rangordning.

I ett oreducerbart rotsystem kan det finnas högst två värden för längden ( α , α ) ^1/2 , motsvarande korta och långa rötter. Om alla rötter har samma längd anses de vara långa per definition och rotsystemet sägs vara helt enkelt spetsat ; detta inträffar i fallen A, D och E. Alla två rötter av samma längd ligger i samma omloppsbana av Weyl-gruppen. I de icke-enkelt spetsade fallen B, C, G och F spänns rotgittret av de korta rötterna och de långa rötterna spänner över ett subgitter, invariant under Weyl-gruppen, lika med r 2 /2 gånger corootgittret ^, där r är längden på en lång rot.

I tabellen intill, |Φ ^< | betecknar antalet korta rötter, I betecknar indexet i undergittrets rotgitter genererat av långa rötter, D betecknar determinanten för Cartan-matrisen och | W | betecknar ordningen för Weyl-gruppen .

Explicit konstruktion av de irreducerbara rotsystemen

A _n

Modell av $A_{3}$ rotsystem i Zometool-systemet

Enkla rötter i A ₃

	e 1	e 2	e 3	e 4
α 1	1	−1	0	0
α 2	0	1	−1	0
α 3	0	0	1	−1

Låt E vara delrummet av R ^{n +1} för vilket koordinaterna summerar till 0, och låt Φ vara mängden vektorer i E med längden √ 2 och som är heltalsvektorer, dvs har heltalskoordinater i R ^{n +1} . En sådan vektor måste ha alla utom två koordinater lika med 0, en koordinat lika med 1 och en lika med −1, så det finns n ² + n rötter i alla. Ett val av enkla rötter uttryckta i standardbasen är α i ₌ e i ₋ e i _{+1 för} 1 ≤ i ≤ n .

Reflexionen σ _i genom hyperplanet vinkelrätt mot α _i är samma som permutation av de intilliggande i: te och ( i + 1): e koordinaterna . Sådana transponeringar genererar hela permutationsgruppen . För intilliggande enkla rötter, σ _i ( α _{i +1} ) = α _{i +1} + α _i = σ _{i +1} ( α _i ) = α _i + α _{i +1} , det vill säga reflektion är ekvivalent med att addera en multipel av 1; men reflektion av en enkel rot vinkelrät mot en icke intilliggande enkel rot lämnar den oförändrad och skiljer sig med en multipel av 0.

An - rotgittret – det vill säga gittret som genereras av A _{n -} rötterna – beskrivs enklast som uppsättningen heltalsvektorer i Rn ^{. +1} vars komponenter summeras till noll

A ₂ rotgittret är vertexarrangemanget för den triangulära plattsättningen .

A ₃ rotgittret är känt för kristallografer som det ansiktscentrerade kubiska (eller kubiskt tätt packade) gittret . Det är vertexarrangemanget för den tetraedriska-oktaedriska honungskakan .

A _3- rotsystemet (liksom de andra rotsystemen i ranking-tre) kan modelleras i Zometool Construction-set .

I allmänhet är A _n rotgittret vertexarrangemanget för den n -dimensionella simplectic honeycomb .

B _n

Enkla rötter i B ₄

	e 1	e 2	e 3	e 4
α 1	1	−1	0	0
α 2	0	1	−1	0
α 3	0	0	1	−1
α 4	0	0	0	1

Låt E = R ⁿ , och låt Φ bestå av alla heltalsvektorer i E med längden 1 eller √ 2 . Det totala antalet rötter är 2 n ² . Ett val av enkla rötter är α _i = e _i – e _{i +1} för 1 ≤ i ≤ n – 1 (ovanstående val av enkla rötter för A _{n −1} ), och den kortare roten α _n = e _n .

Reflexionen σ _n genom hyperplanet vinkelrätt mot den korta roten α _n är naturligtvis helt enkelt negation av den n :te koordinaten. För den långa enkla roten α _{n −1} , σ _{n −1} ( α _n ) = α _n + α _{n −1} , men för reflektion vinkelrätt mot den korta roten, σ _n ( α _{n −1} ) = α _{n −1} + 2 α _n , en skillnad med en multipel av 2 istället för 1.

B n rotgittret - det vill säga gittret som genereras av B _{n rötterna - består av} alla heltalsvektorer.

B ₁ är isomorf till A ₁ via skalning med √ 2 , och är därför inte ett distinkt rotsystem.

C _n

Rotsystem B ₃ , C ₃ , och A ₃ = D ₃ som punkter inom en kub och oktaeder

Enkla rötter i C ₄

	e 1	e 2	e 3	e 4
α 1	1	−1	0	0
α 2	0	1	−1	0
α 3	0	0	1	−1
α 4	0	0	0	2

Låt E = R ⁿ , och låt Φ bestå av alla heltalsvektorer i E med längden √ 2 tillsammans med alla vektorer av formen 2 λ , där λ är en heltalsvektor med längden 1. Det totala antalet rötter är 2 n ² . Ett val av enkla rötter är: α _i = e _i − e _{i +1} , för 1 ≤ i ≤ n − 1 (ovanstående val av enkla rötter för A _{n −1} ), och den längre roten α _n = 2 e _n . Reflexionen σ _n ( α _{n −1} ) = α _{n −1} + α _n , men σ _{n −1} ( α _n ) = α _n + 2 α _{n −1} .

C _n rotgittret – det vill säga gittret som genereras av C _n rötterna – består av alla heltalsvektorer vars komponenter summeras till ett jämnt heltal .

C ₂ är isomorf till B ₂ via skalning med √ 2 och en 45 graders rotation, och är därför inte ett distinkt rotsystem.

D _n

Enkla rötter i D ₄

	e 1	e 2	e 3	e 4
α 1	1	−1	0	0
α 2	0	1	−1	0
α 3	0	0	1	−1
α 4	0	0	1	1

Låt E = R ⁿ , och låt Φ bestå av alla heltalsvektorer i E med längden √ 2 . Det totala antalet rötter är 2 n ( n − 1) . Ett val av enkla rötter är α _i = e _i − e _{i +1} för 1 ≤ i ≤ n − 1 (ovanstående val av enkla rötter för A _{n −1} ) tillsammans med α _n = e _{n −1} + e _n .

Reflektion genom hyperplanet vinkelrätt mot α _n är detsamma som att transponera och negera de intilliggande n -:e och ( n - 1) - koordinaterna. Varje enkel rot och dess reflektion vinkelrätt mot en annan enkel rot skiljer sig med en multipel av 0 eller 1 av den andra roten, inte med någon större multipel.

D _n rotgittret – det vill säga gittret som genereras av D _n rötterna – består av alla heltalsvektorer vars komponenter summeras till ett jämnt heltal . Detta är samma som C _n rotgittret.

D n rötterna uttrycks som hörn av ett rätat n - ortoplex , Coxeter –Dynkin diagram _: ... . De 2 n ( n − 1) hörnen finns i mitten av kanterna på n -ortoplexet.

D ₃ sammanfaller med A ₃ , och är därför inte ett distinkt rotsystem. De tolv D ₃ rotvektorerna uttrycks som hörn av , en lägre symmetrikonstruktion av kuboktaedern .

D ₄ har ytterligare symmetri som kallas trialitet . De tjugofyra D ₄ rotvektorerna uttrycks som hörn av , en lägre symmetrikonstruktion av 24-cellen .

E6 , E7 , E8 _{_ _ _}

72 hörn av 1 22 representerar rotvektorerna för E 6 (Gröna noder dubbleras i denna E6 Coxeter-planprojektion)	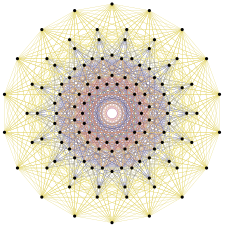126 hörn av 2 31 representerar rotvektorerna för E 7	240 hörn av 4 21 representerar rotvektorerna för E 8

• E ₈ rotsystemet är vilken uppsättning vektorer som helst i R ⁸ som är kongruenta med följande uppsättning:
  $$D_{8}\cup \left\{{\frac {1}{2}}\left(\sum _{i=1}^{8}\varepsilon _{i}\mathbf {e} _ {i}\right):\varepsilon _{i}=\pm 1,\,\varepsilon _{1}\cdots \varepsilon _{8}=+1\right\}.$$

Rotsystemet har 240 rötter. Uppsättningen som just listats är uppsättningen vektorer med längden √ 2 i E8-rotgittret, även känt som E8-gittret eller Γ ₈ . Detta är uppsättningen av punkter i R ⁸ så att:

1. alla koordinater är heltal eller alla koordinater är halvheltal (en blandning av heltal och halvheltal är inte tillåten), och
2. summan av de åtta koordinaterna är ett jämnt heltal .

Således,

$$E_{8}=\left\{\alpha \in \mathbb {Z} ^{8}\cup \left(\mathbb {Z} +{\tfrac {1}{2}}\right) ^{8}:|\alpha |^{2}=\summa \alpha _{i}^{2}=2,\,\summa \alpha _{i}\i 2\mathbb {Z} .\right \}$$

• Rotsystemet E ₇ är uppsättningen vektorer i E ₈ som är vinkelräta mot en fixerad rot i E ₈ . Rotsystemet E ₇ har 126 rötter.
• Rotsystemet E ₆ är inte uppsättningen av vektorer i E ₇ som är vinkelräta mot en fixerad rot i E ₇ , faktiskt, man får D ₆ på det sättet. Emellertid E ₆ delsystemet av E ₈ vinkelrätt mot två lämpligt valda rötter av E ₈ . Rotsystemet E ₆ har 72 rötter.

Enkla rötter i E ₈ : jämna koordinater

1	−1	0	0	0	0	0	0
0	1	−1	0	0	0	0	0
0	0	1	−1	0	0	0	0
0	0	0	1	−1	0	0	0
0	0	0	0	1	−1	0	0
0	0	0	0	0	1	−1	0
0	0	0	0	0	1	1	0
−1/2	−1/2	−1/2	−1/2	−1/2	−1/2	−1/2	−1/2

En alternativ beskrivning av E ₈ -gittret som ibland är praktiskt är som mängden Γ' ₈ av alla punkter i R ⁸ så att

• alla koordinater är heltal och summan av koordinaterna är jämn, eller
• alla koordinaterna är halvheltal och summan av koordinaterna är udda.

Gittren _Γ8 och Γ'8 är isomorfa _; man kan gå från den ena till den andra genom att ändra tecknen på vilket udda antal koordinater som helst. Gittret Γ ₈ kallas ibland det jämna koordinatsystemet för E ₈ medan gittret Γ' ₈ kallas det udda koordinatsystemet .

Ett val av enkla rötter för E ₈ i det jämna koordinatsystemet med rader ordnade efter nodordning i de alternativa (icke-kanoniska) Dynkin-diagrammen (ovan) är:

α _i = e _i − e _{i +1} , för 1 ≤ i ≤ 6, och

α ₇ = e ₇ + e ₆

(ovanstående val av enkla rötter för D ₇ ) tillsammans med

$$\mathbf {\alpha } _{8}=\mathbf {\beta } _{0}=-{\frac {1}{2}}\left(\sum _{i=1}^{8 }e_{i}\right)=(-1/2,-1/2,-1/2,-1/2,-1/2,-1/2,-1/2,-1/2) .$$

Enkla rötter i E ₈ : udda koordinater

1	−1	0	0	0	0	0	0
0	1	−1	0	0	0	0	0
0	0	1	−1	0	0	0	0
0	0	0	1	−1	0	0	0
0	0	0	0	1	−1	0	0
0	0	0	0	0	1	−1	0
0	0	0	0	0	0	1	−1
−1/2	−1/2	−1/2	−1/2	−1/2	1/2	1/2	1/2

Ett val av enkla rötter för E ₈ i det udda koordinatsystemet med rader ordnade efter nodordning i alternativa (icke-kanoniska) Dynkin-diagram (ovan) är

α _i = e _i − e _{i +1} , för 1 ≤ i ≤ 7

(ovan val av enkla rötter för A ₇ ) tillsammans med

α ₈ = β ₅ , där

β _j = ${\textstyle {\frac {1}{2}}\left(-\sum _{i=1}^{j}e_{i}+\summa _{i=j+1}^{8}e_{ i}\right).}$

(Att använda β ₃ skulle ge ett isomorft resultat. Att använda β _1,7 eller β _2,6 skulle helt enkelt ge A ₈ eller D ₈ . När det gäller β ₄ , summeras dess koordinater till 0, och detsamma gäller för α _{1.. .7} , så de spänner bara över det 7-dimensionella underrummet för vilket koordinaterna summerar till 0; i själva verket har −2 β ₄ koordinater (1,2,3,4,3,2,1) i basen ( α _i ) .)

Eftersom vinkelräthet mot α ₁ betyder att de två första koordinaterna är lika, är E ₇ då delmängden av E ₈ där de två första koordinaterna är lika, och på samma sätt är E ₆ delmängden av E ₈ där de första tre koordinaterna är lika. Detta underlättar explicita definitioner av E ₇ och E ₆ som

E ₇ = { α ∈ Z ⁷ ∪ ( Z +1/2) ⁷ : Σ α _i ² + α ₁ ² = 2, Σ α _i + α ₁ ∈ 2 Z },

E ₆ = { α ∈ Z ⁶ ∪ ( Z +1/2) ⁶ : Σ αi ² + 2 _α 1 ₂ ⁼ 2, Σ α _i + 2 _α 1 ∈ 2 Z }

Observera att radering av α ₁ och sedan α ₂ ger uppsättningar av enkla rötter för E ₇ och E ₆ . Dessa uppsättningar av enkla rötter finns emellertid i andra E ₇ och E ₆ underrum av E ₈ än de som skrivs ovan, eftersom de inte är ortogonala mot α ₁ eller α ₂ .

F ₄

Enkla rötter i F ₄

	e 1	e 2	e 3	e 4
α 1	1	−1	0	0
α 2	0	1	−1	0
α 3	0	0	1	0
α 4	−1/2	−1/2	−1/2	−1/2

48-rotsvektorer av F4, definierade av hörn av 24-cellen och dess dubbla, sett i Coxeter-planet

För F ₄ , låt E = R ⁴ och låt Φ beteckna uppsättningen av vektorer α med längden 1 eller √ 2 så att koordinaterna för 2α är heltal och är antingen alla jämna eller udda. Det finns 48 rötter i detta system. Ett val av enkla rötter är: valet av enkla rötter som ges ovan för B ₃ , plus ${\textstyle {\boldsymbol {\alpha }}_{4}=-{ \frac {1}{2}}\sum _{i=1}^{4}e_{i}}$ .

F ₄ rotgittret - det vill säga gittret som genereras av F ₄ rotsystemet - är uppsättningen av punkter i R 4 ^så att antingen alla koordinater är heltal eller alla koordinater är halvheltal (en blandning av heltal och hälften -heltal är inte tillåtna). Detta gitter är isomorft mot gittret av Hurwitz quaternions .

G ₂

Enkla rötter i G ₂

	e 1	e 2	e 3
α 1	1	−1	0
β	−1	2	−1

Rotsystemet G ₂ har 12 rötter, som bildar hörnen på ett hexagram . Se bilden ovan .

Ett val av enkla rötter är ( α ₁ , β = α ₂ − α ₁ ) där α _i = e _i − e _{i +1} för i = 1, 2 är ovanstående val av enkla rötter för A ₂ .

G ₂ rotgittret – det vill säga gittret som genereras av G ₂ rötterna – är detsamma som A 2 _rotgittret .

Rotposetten

Hasse-diagram av E6 rotposet med kantetiketter som identifierar tillagd enkel rotposition

Mängden positiva rötter ordnas naturligt genom att säga att $\alpha \leq \beta$ om och endast om $\beta -\alpha$ är en icke-negativ linjär kombination av enkla rötter. Denna poset är graderad av ${\textstyle \deg \left(\sum _{\alpha \in \Delta }\lambda _{\alpha }\ alpha \right)=\sum _{\alpha \in \Delta }\lambda _{\alpha }} ,$ och har många anmärkningsvärda kombinatoriska egenskaper, en av dem är att man kan bestämma graderna av de fundamentala invarianterna för motsvarande Weyl grupp från denna post. Hasse-grafen är en visualisering av ordningen av rotposet.

Se även

• ADE-klassificering
• Affint rotsystem
• Coxeter–Dynkin diagram
• Coxeter grupp
• Coxeter matris
• Dynkin diagram
• rotdatum
• Semienkel Lie-algebra
• Vikter i representationsteorin för semisimpla Lie-algebror
• Rotsystem av en semi-enkel Lie-algebra
• Weyl-gruppen

Anteckningar

•   Adams, JF (1983), föreläsningar om lögngrupper , University of Chicago Press, ISBN 0-226-00530-5
•   Bourbaki, Nicolas (2002), Lie groups and Lie algebras, Kapitel 4–6 (översatt från 1968 års franska original av Andrew Pressley), Elements of Mathematics, Springer-Verlag, ISBN 3-540-42650-7 . Den klassiska referensen för rotsystem.
•   Bourbaki, Nicolas (1998). Element i matematikens historia . Springer. ISBN 3540647678 .
• Coleman, AJ (sommaren 1989), "The greatest matematical paper of all time", The Mathematical Intelligencer , 11 (3): 29–38, doi : 10.1007/bf03025189
•   Hall, Brian C. (2015), Lie groups, Lie algebras, and representations: An elementary introduction , Graduate Texts in Mathematics, vol. 222 (andra upplagan), Springer, ISBN 978-3319134666
•   Humphreys, James (1972). Introduktion till Liealgebror och representationsteori . Springer. ISBN 0387900535 .
•   Humphreys, James (1992). Reflektionsgrupper och Coxetergrupper . Cambridge University Press. ISBN 0521436133 .
•   Killing, Wilhelm (juni 1888). "Die Zusammensetzung der stetigen endlichen Transformationsgruppen" . Matematiska Annalen . 31 (2): 252–290. doi : 10.1007/BF01211904 . S2CID 120501356 . Arkiverad från originalet 2016-03-05.
  • — (mars 1888). "Del 2" . Matematik. Ann . 33 (1): 1–48. doi : 10.1007/BF01444109 .
  • — (mars 1889). "Del 3" . Matematik. Ann . 34 (1): 57–122. doi : 10.1007/BF01446792 . Arkiverad från originalet 2015-02-21.
  • — (Juni 1890). "Del 4" . Matematik. Ann . 36 (2): 161–189. doi : 10.1007/BF01207837 .
•   Kac, Victor G. (1990). Infinite-Dimensional Lie Algebras (3:e upplagan). Cambridge University Press. ISBN 978-0-521-46693-6 .
•   Springer, TA (1998). Linjära algebraiska grupper (2:a upplagan). Birkhäuser. ISBN 0817640215 .

Vidare läsning

•   Dynkin, EB (1947). "Strukturen av semi-enkla algebror" . Uspekhi Mat. Nauk . 2 (på ryska). 4 (20): 59–127. MR 0027752 .