Geodetisk polyeder
|
||||
|
||||
En geodetisk polyeder är en konvex polyeder gjord av trianglar. De har vanligtvis icosahedral symmetri , så att de har 6 trianglar vid en vertex, förutom 12 hörn som har 5 trianglar. De är dualen av motsvarande Goldberg-polyedrar med mestadels sexkantiga ytor.
Geodetiska polyedrar är en bra approximation till en sfär för många ändamål, och förekommer i många olika sammanhang. De mest kända kan vara de geodetiska kupolerna designade av Buckminster Fuller , vilka geodetiska polyedrar är uppkallade efter. Geodetiska rutnät som används i geodesi har också geometrin för geodetiska polyedrar. Kapsiderna hos vissa virus har formen av geodetiska polyedrar, och fullerenmolekyler har formen av Goldberg- polyedrar . Geodesiska polyedrar är tillgängliga som geometriska primitiver i Blender 3D-modelleringsmjukvarupaketet, som kallar dem icospheres : de är ett alternativ till UV-sfären , med en mer regelbunden fördelning av hörn än UV-sfären. Goldberg -Coxeter-konstruktionen är en utökning av begreppen bakom geodetiska polyedrar.
Geodesisk notation
I Magnus Wenningers sfäriska modeller ges polyedrar geodetisk notation i formen {3, q +} b , c , där {3, q } är Schläfli-symbolen för den regelbundna polyedern med triangulära ytor och q- valenshörn . Symbolen + indikerar valensen av de hörn som ökas. b , c representerar en underavdelningsbeskrivning, där 1,0 representerar basformen. Det finns 3 symmetriklasser av former: {3,3+} 1,0 för en tetraeder , {3,4+} 1,0 för en oktaeder och {3,5+} 1,0 för en ikosaeder .
Den dubbla notationen för Goldberg-polyedrar är { q +,3} b , c , med valens-3 hörn, med q -gonala och hexagonala ytor. Det finns 3 symmetriklasser av former: {3+,3} 1,0 för en tetraeder , {4+,3} 1,0 för en kub och {5+,3} 1,0 för en dodekaeder .
Värden för b , c är indelade i tre klasser:
- Klass I (b=0 eller c=0): {3, q +} b ,0 eller {3, q +} 0, b representerar en enkel division där originalkanterna är uppdelade i b underkanter.
- Klass II (b=c): {3, q +} b , b är lättare att se från den dubbla polyedern { q ,3} med q -gonala ytor först uppdelade i trianglar med en central punkt, och sedan delas alla kanter i b underkanter.
- Klass III : {3, q +} b , c har ojämna värden som inte är noll för b , c , och existerar i kirala par. För b > c kan vi definiera det som en högerhänt form, och c > b är en vänsterhänt form.
Underavdelningar i klass III här stämmer inte helt överens med originalkanterna. Undernäten kan extraheras genom att titta på en triangulär plattsättning , placera en stor triangel ovanpå rutnätets hörn och gångvägar från en vertex b steg i en riktning, och en sväng, antingen medurs eller moturs, och sedan en annan c steg till nästa primära vertex.
Till exempel är ikosaedern {3,5+} 1,0 , och pentakis dodecahedron , {3,5+} 1,1 ses som en vanlig dodekaeder med femkantiga ytor uppdelade i 5 trianglar.
Den primära ytan av underavdelningen kallas en huvudsaklig polyedrisk triangel (PPT) eller nedbrytningsstrukturen . Genom att beräkna en enda PPT kan hela figuren skapas.
Frekvensen för en geodetisk polyeder definieras av summan av ν = b + c . En överton är en underfrekvens och kan vara vilken hel divisor som helst av ν . Klass II har alltid en överton på 2, eftersom ν = 2 b .
Trianguleringstalet är T = b 2 + bc + c 2 . _ Detta antal gånger antalet ursprungliga ansikten uttrycker hur många trianglar den nya polyedern kommer att ha.

|
Element
Antalet element anges av trianguleringstalet . Två olika geodetiska polyedrar kan ha samma antal element, till exempel {3,5+} 5,3 och {3,5+} 7,0 har båda T=49.
| Symmetri | Icosahedral | Octaedral | Tetraedrisk |
|---|---|---|---|
| Bas |
Icosahedron {3,5} = {3,5+} 1,0 |
Oktaeder {3,4} = {3,4+} 1,0 |
Tetraeder {3,3} = {3,3+} 1,0 |
| Bild |

|

|

|
| Symbol | {3,5+} b , c | {3,4+} b , c | {3,3+} b , c |
| Vertices | |||
| Ansikten | |||
| Kanter |
Konstruktion
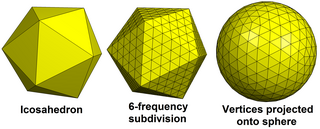
Geodetiska polyedrar är konstruerade genom att dela upp ytor av enklare polyedrar och sedan projicera de nya hörnen på ytan av en sfär. En geodetisk polyeder har raka kanter och plana ytor som närmar sig en sfär, men den kan också göras som en sfärisk polyeder (en tessellation på en sfär ) med äkta geodetiska böjda kanter på ytan av en sfär och sfäriska triangelytor .
| Conway | u 3 I = (kt)I | (k)tI | ktI | |
|---|---|---|---|---|
| Bild |  |
 |
 |
|
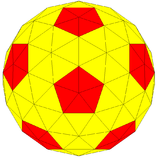
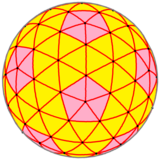
| Form |
3-frekvens uppdelad icosahedron |
Kis stympad icosahedron | Geodesisk polyeder (3,0) | Sfärisk polyeder |
I detta fall, {3,5+} 3,0 , med frekvensen och trianguleringstalet , har var och en av de fyra versionerna av polygonen 92 hörn (80 där sex kanter förenas och 12 där fem sammanfogas), 270 kanter och 180 ytor.
Relation till Goldberg polyhedra
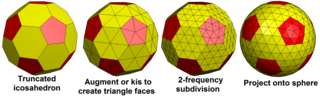
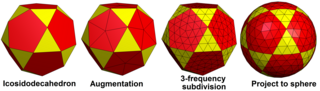
Geodesiska polyedrar är dualerna av Goldberg-polyedrar. Goldberg-polyedrar är också besläktade genom att applicering av en kis-operator (dela yttrianglar med en mittpunkt) skapar nya geodetiska polyedrar, och trunkering av hörn på en geodetisk polyeder skapar en ny Goldberg-polyeder. Till exempel, Goldberg G(2,1) kised , blir {3,5+} 4,1 , och trunkering som blir G(6,3). Och på samma sätt blir {3,5+} 2,1 trunkerad G(4,1), och den kised blir {3,5+} 6,3 .
Exempel
Klass I
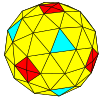
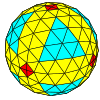
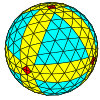
| Frekvens | (1,0) | (2,0) | (3,0) | (4,0) | (5,0) | (6,0) | (7,0) | (8,0) | ( m ,0) |
|---|---|---|---|---|---|---|---|---|---|
| T | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | m 2 |
|
Ansiktstriangel _ |
 |
 |
 |
 |
 |
 |
 |
 |
... |
| Icosahedral |

|

|

|

|

|

|

|

|
Mer |
| Octaedral |

|

|

|
|

|
|

|
|
Mer |
| Tetraedrisk |

|

|

|

|

|
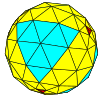
|
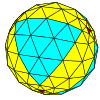
|

|
Mer |
Klass II
| Frekvens | (1,1) | (2,2) | (3,3) | (4,4) | (5,5) | (6,6) | (7,7) | (8,8) | ( m , m ) |
|---|---|---|---|---|---|---|---|---|---|
| T | 3 | 12 | 27 | 48 | 75 | 108 | 147 | 192 | 3 m 2 |
|
Ansiktstriangel _ |
 |
 |
 |
 |
 |
 |
 |
 |
... |
| Icosahedral |

|

|

|
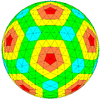
|

|
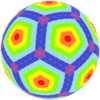
|

|

|
Mer |
| Octaedral |

|

|
Mer | ||||||
| Tetraedrisk |

|
Mer |
Klass III
| Frekvens | (2,1) | (3,1) | (3,2) | (4,1) | (4,2) | (4,3) | (5,1) | (5,2) | ( m , n ) |
|---|---|---|---|---|---|---|---|---|---|
| T | 7 | 13 | 19 | 21 | 28 | 37 | 31 | 39 | m 2 + mn + n 2 |
|
Ansiktstriangel _ |
 |
 |
 |
 |
 |
 |
 |
 |
... |
| Icosahedral |

|

|

|

|

|
Mer | |||
| Octaedral |

|
Mer | |||||||
| Tetraedrisk |

|
Mer |
Sfäriska modeller
Magnus Wenningers bok Spherical Models utforskar dessa underavdelningar i att bygga polyedermodeller . Efter att ha förklarat konstruktionen av dessa modeller förklarade han sin användning av triangulära rutnät för att markera mönster, med trianglar färgade eller uteslutna i modellerna.
 En konstnärlig modell skapad av fader Magnus Wenninger kallad Order in Chaos , som representerar en kiral delmängd av trianglar av en 16-frekvent ikosaedrisk geodesisk sfär , {3,5+} 16,0 |
 En virtuell kopia som visar stora cirklar med icosahedrisk symmetri . Den 6-faldiga rotationssymmetrin är illusionär och existerar inte på själva ikosaedern. |
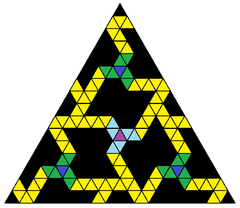 En enda ikosaedrisk triangel med en 16-frekvens underavdelning |
Se även
- Robert Williams The Geometrical Foundation of Natural Structure: A source book of Design , 1979, s. 142–144, figur 4-49,50,51 Custers of 12 spheres, 42 spheres, 92 spheres
- Antony Pugh, Polyhedra: a visual approach , 1976, kapitel 6. The Geodesic Polyhedra of R. Buckminster Fuller and Related Polyhedra
- Wenninger, Magnus (1979), Spherical Models , Cambridge University Press , ISBN 978-0-521-29432-4 , MR 0552023 , arkiverad från originalet den 4 juli 2008 Återtryckt av Dover 1999 ISBN 978-40-916- 4
- Edward S. Popko, Divided spheres: Geodesics & the Orderly Subdivision of the Sphere (2012) Kapitel 8 Subdivision schemas, 8.1 Geodesic Notation, 8.2 Triangulation number 8.3 Frequency and Harmonics 8.4 Grid Symmetry 8.5 Class I: Alternates the5 and for. Huvudtriangel 8.5.2 Kantreferenspunkter