Kantellation (geometri)

En kantellerad kub - Röda ansikten reduceras. Kanterna är fasade och bildar nya gula fyrkantiga ytor. Vertices är trunkerade och bildar nya blå triangelytor.

En kantellerad kubisk honungskaka - Lila kuber är kantellerade. Kanterna är fasade och bildar nya blå kubiska celler. Vertices trunkeras och bildar nya röda rätade kubceller .

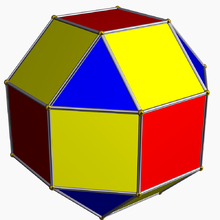
Inom geometri är en kantellation en trunkering av andra ordningen i valfri dimension som avfasar en vanlig polytop vid dess kanter och vid dess hörn , vilket skapar en ny facett i stället för varje kant och varje vertex. Kantellering gäller även för vanliga plattsättningar och vaxkakor . Att kantellera en polyeder är också att korrigera dess likriktning .

Kantellation (för polyedrar och plattsättningar) kallas även expansion av Alicia Boole Stott : det motsvarar att flytta den vanliga formens ytor bort från mitten och fylla i en ny yta i springan för varje öppnad kant och för varje öppnad vertex.

Notation

En kantellerad polytop representeras av en utökad Schläfli-symbol t _0,2 { p , q ,...} eller r ${\begin{Bmatrix}p\\q\\...\end{Bmatrix}}$ eller rr { p , q ,...}.

För polyeder erbjuder en kantellation en direkt sekvens från en vanlig polyeder till dess dubbla .

Exempel: kantellationssekvens mellan kub och oktaeder:

Exempel: en kuboktaeder är en kantellerad tetraeder .

För högredimensionella polytoper erbjuder en kantellation en direkt sekvens från en vanlig polytop till dess dubbelräktade form.

Exempel: kantellerande polyedrar, plattsättningar

Vanliga polyedrar, vanliga plattsättningar

Form	Polyedra			Kakelplattor
Coxeter	rTT	rCO	befria	rQQ	rHA
Conway notation	eT	eC = eO	eI = eD	eQ	eH = eA
Polyedrar som ska expanderas	Tetraeder	Kub eller oktaeder	Ikosaeder eller dodekaeder	Fyrkantig kakel	Sexkantigt kakel Triangulärt kakel
Bildanimering
_

Uniforma polyedrar eller deras dualer

Coxeter	rrt{2,3}	rrs{2,6}	rrCO	rrID
Conway notation	eP3	eA4	eaO = eaC	eaI = eaD
Polyedrar som ska expanderas	Triangulärt prisma eller triangulärt bipyramid	Fyrkantig antiprisma eller tetragonal trapezhedron	Cuboctahedron eller rombisk dodekaeder	Icosidodecahedron eller rombisk triacontahedron
Bildanimering
_

Se även

• Uniform polyeder
• Uniform 4-polytop
• Fasning (geometri)

•   Coxeter, HSM Regular Polytopes , (3:e upplagan, 1973), Dover-upplagan, ISBN 0-486-61480-8 (s.145-154 Kapitel 8: Truncation, s 210 Expansion)
• Norman Johnson Uniform Polytopes , Manuscript (1991)
  • NW Johnson : Theory of Uniform Polytopes and Honeycombs , Ph.D. Avhandling, University of Toronto, 1966

externa länkar

• Weisstein, Eric W. "Expansion" . MathWorld .