Alternering (geometri)

Växling av en kub skapar en tetraeder .

Alternering av en trunkerad kuboktaeder skapar en ojämn kub .

Inom geometri är en alternering eller partiell trunkering en operation på en polygon , polyeder , plattsättning eller högre dimensionell polytop som tar bort alternativa hörn.

Coxeter betecknar en växling med ett prefixet h , vilket står för halva eller halva . Eftersom växling reducerar alla polygonytor till hälften så många sidor, kan den endast tillämpas på polytoper med alla jämna sidor. En alternerad fyrkantig yta blir en digon , och är degenererad, reduceras vanligtvis till en enda kant.

Mer generellt kan vilken vinkelformig polyeder eller kakel som helst med en vertexkonfiguration som består av alla element med jämna nummer alterneras . Till exempel är växlingen av en vertexfigur med 2a.2b.2c a.3.b.3.c.3 där de tre är antalet element i denna vertexfigur. Ett specialfall är fyrkantiga ansikten vars ordning delar sig på mitten i degenererade digoner . Så till exempel, kuben 4.4.4 alterneras som 2.3.2.3.2.3 som reduceras till 3.3.3, som är tetraedern , och alla 6 kanter på tetraedrarna kan också ses som de degenererade ytorna på den ursprungliga kuben.

Nonchalera

Ytterligare information: Snub (geometri)

En snub (i Coxeters terminologi ) kan ses som en växling av en trunkerad regelbunden eller trunkerad kvasiregelbunden polyeder. I allmänhet kan en polyeder avstannas om dess trunkering endast har jämna ytor. Alla stympade räta polyedrar kan snubbas, inte bara från vanliga polyedrar.

Antiprismat för snubkant är ett exempel på en allmän snubbning och kan representeras av ss{2,4}, med kvadratiskt antiprisma s{2,4}.

Alternerade polytoper

Denna växlingsoperation gäller även för högredimensionella polytoper och bikakor, men i allmänhet kommer de flesta resultaten av denna operation inte att vara enhetliga. De tomrum som skapas av de borttagna hörnen kommer i allmänhet inte att skapa enhetliga aspekter, och det finns vanligtvis inte tillräckligt med frihetsgrader för att tillåta en lämplig omskalning av de nya kanterna. Undantag finns dock, såsom härledningen av snub 24-cellen från den trunkerade 24-cellen .

Exempel:

• Honeycombs
  1. En alternerad kubisk honeycomb är den tetraedriska-oktaedriska bikakan .
  2. En alternerad hexagonal prismatisk honeycomb är den roterande alternerade kubiska bikakan .
• 4-polytop
  1. En alternerad trunkerad 24-cell är snub 24-cell .
• 4-celliga honeycomb:
  1. En alternerad trunkerad 24-cells honeycomb är den snubbade 24-cells honeycomb .
• En hyperkub kan alltid alterneras till en enhetlig demihyperkub .
  1. Kub → Tetraeder (vanlig)
     • →
  2. Tesseract ( 8-celler ) → 16-celler (vanliga)
     • →
  3. Penteract → demipenteract (halvregelbunden)
  4. Hexeract → demihexeract (uniform)
  5. ...

Förändrade polyedrar

Coxeter använde också operatorn a , som innehåller båda halvorna, så att den ursprungliga symmetrin behålls. För regelbundna polyedrar med jämna sidor representerar a{2p,q} en sammansatt polyeder med två motsatta kopior av h{2p,q}. För udda sidor, större än 3, blir vanliga polyedrar a{p,q} en stjärnpolyeder .

Norman Johnson utökade användningen av den ändrade operatorn a {p,q}, b {p,q} för blandad , och c {p,q} för konverterad , som , , och respektive.

Den sammansatta polyedern känd som den stellerade oktaedern kan representeras av en {4,3} (en förändrad kub ), och , .

Stjärnpolyedern känd som den lilla ditrigonala icosidodecahedronen kan representeras av en{5,3} (en förändrad dodekaeder ), och , . Här har alla femhörningar alternerats till pentagram, och trianglar har infogats för att ta upp de resulterande fria kanterna.

Stjärnpolyedern känd som den stora ditrigonala icosidodecahedronen kan representeras av en{5/2,3} (en förändrad stor stellerad dodekaeder ), och , . Här har alla pentagram alternerats tillbaka till femhörningar, och trianglar har infogats för att ta upp de resulterande fria kanterna.

Alternativa trunkationer

En liknande operation kan trunkera alternativa hörn, snarare än att bara ta bort dem. Nedan finns en uppsättning polyedrar som kan genereras från katalanska fasta ämnen . Dessa har två typer av hörn som omväxlande kan trunkeras. Trunkering av "högre ordningens" hörn och båda vertextyperna ger dessa former:

namn	Original	Alternerad trunkering	Avkortning	Trunkerat namn
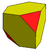
Kub Dual av rätad tetraeder				Alternativ stympad kub
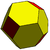
Rombisk dodekaeder Dubbel av kuboktaeder				Stympad rombisk dodekaeder
Rombisk triacontahedron Dual av icosidodecahedron				Stympad rombisk triakontaeder
Triakis tetraeder Dubbel av trunkerad tetraeder				Stympad triakistetraeder
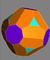
Triakis oktaeder Dubbel av trunkerad kub				Stympad triakis oktaeder
Triakis icosahedron Dubbel av trunkerad dodekaeder				Stympad triakis icosahedron

Se även

• Conway polyedrisk notation
• Wythoff konstruktion

•   Coxeter, HSM Regular Polytopes , (3:e upplagan, 1973), Dover-upplagan, ISBN 0-486-61480-8
• Norman Johnson Uniform Polytopes , Manuscript (1991)
  • NW Johnson : Theory of Uniform Polytopes and Honeycombs , Ph.D. Avhandling, University of Toronto, 1966
• Weisstein, Eric W. "Snubification" . MathWorld .
• Richard Klitzing, Snubs, alternated facetings, and Stott-Coxeter-Dynkin diagrams , Symmetry: Culture and Science, Vol. 21, No.4, 329-344, (2010) [1]

externa länkar

• Olshevsky, George. "Alternativ" . Ordlista för Hyperspace . Arkiverad från originalet den 4 februari 2007.
• Polyedernamn, snubb

Polyederoperatörer

Utsäde	Avkortning	Rättelse	Bitrunkation	Dubbel	Expansion	Omnitruncation	Växlingar
0 t { p , q } { p , q }	t 01 { p , q } t { p , q }	t 1 { p , q } r { p , q }	t 12 { p , q } 2t { p , q }	t 2 { p , q } 2r { p , q }	t 02 { p , q } rr { p , q }	t 012 { p , q } tr { p , q }	0 ht { p , q } h { q , p }	ht 12 { p , q } s { q , p }	ht 012 { p , q } sr { p , q }