Lista över enhetliga polyedrar av Schwarz triangel

Coxeters listning av degenererade Wythoffian likformiga polyedrar, som ger Wythoff-symboler, vertexfigurer och beskrivningar med Schläfli-symboler . Alla de likformiga polyedrarna och alla degenererade Wythoffian likformiga polyedrarna listas i den här artikeln.

Det finns många släktskap mellan de enhetliga polyedrarna . Wythoff -konstruktionen kan konstruera nästan alla de enhetliga polyedrarna från de spetsiga och trubbiga Schwarz-trianglarna . Siffrorna som kan användas för sidorna av en icke- dihedrisk akut eller trubbig Schwarz-triangel som inte nödvändigtvis leder till endast degenererade enhetliga polyedrar är 2, 3, 3/2, 4, 4/3, 5, 5/2, 5/3 och 5/4 (men siffror med täljare 4 och de med täljare 5 får inte förekomma tillsammans). (4/2 kan också användas, men leder bara till degenererade enhetliga polyedrar då 4 och 2 har en gemensam faktor.) Det finns 44 sådana Schwarz-trianglar (5 med tetraedrisk symmetri , 7 med oktaedrisk symmetri och 32 med icosaedrisk symmetri ), som , tillsammans med den oändliga familjen av dihedriska Schwarz-trianglar, kan bilda nästan alla de icke- degenererade enhetliga polyedrarna. Många degenererade enhetliga polyedrar, med helt sammanfallande hörn, kanter eller ytor, kan också genereras av Wythoff-konstruktionen, och de som uppstår från Schwarz-trianglar som inte använder 4/2 anges också i tabellerna nedan tillsammans med deras icke-degenererade motsvarigheter . Reflex Schwarz trianglar har inte inkluderats, eftersom de helt enkelt skapar dubbletter eller degenererar; dock nämns några få utanför tabellerna på grund av deras tillämpning på tre av de snubbade polyedrarna .

Det finns några icke-wythoffska enhetliga polyedrar, som inga Schwarz-trianglar kan generera; de flesta av dem kan dock genereras med Wythoff-konstruktionen som dubbla höljen (den icke-Wythoffska polyedern täcks två gånger istället för en gång) eller med flera ytterligare sammanfallande ytor som måste kasseras för att inte lämna mer än två ytor vid varje kant (se Omnitruncated polyhedron#Andra jämnsidiga icke-konvexa polyedrar ). Sådana polyedrar är markerade med en asterisk i denna lista. De enda enhetliga polyedrarna som fortfarande misslyckas med att genereras av Wythoff-konstruktionen är den stora dirhombicosidodecahedronen och den stora disnub dirhombidodecahedronen .

Varje sida av Schwarz-trianglar på en sfär kan täcka sfären bara en gång, eller så kan den istället slingra sig runt sfären ett helt antal gånger och korsa sig själv i processen. Antalet gånger som plattsättningen slingrar sig runt sfären är plattsättningens densitet och betecknas μ.

Jonathan Bowers korta namn för polyedrarna, kända som Bowers akronymer, används istället för de fullständiga namnen för polyedrarna för att spara utrymme. Maeder-indexet ges också. Förutom de dihedriska Schwarz-trianglarna är Schwarz-trianglarna ordnade efter sin täthet.

De analoga fallen av euklidiska plattsättningar är också listade, och de av hyperboliska plattsättningar diskuteras kort och ofullständigt.

Möbius och Schwarz trianglar

Det finns fyra sfäriska trianglar med vinklarna π/p, π/q, π/r, där (pqr) är heltal: ( Coxeter , "Uniform polyhedra", 1954)

1. (2 2 r) - Dihedral
2. (2 3 3) - Tetraedrisk
3. (2 3 4) - Octahedral
4. (2 3 5) - Icosahedral

Dessa kallas för Möbius-trianglar.

Dessutom överväger Schwarz-trianglar (pqr) som är rationella tal. Var och en av dessa kan klassificeras i en av de 4 uppsättningarna ovan.

Densitet (μ)	Dihedral	Tetraedrisk	Octaedral	Icosahedral
d	(2 2 n / d )
1		(2 3 3)	(2 3 4)	(2 3 5)
2		(3/2 3 3)	(3/2 4 4)	(3/2 5 5), (5/2 3 3)
3		(2 3/2 3)		(2 5/2 5)
4			(3 4/3 4)	(3 5/3 5)
5		(2 3/2 3/2)	(2 3/2 4)
6		(3/2 3/2 3/2)		(5/2 5/2 5/2), (3/2 3 5), (5/4 5 5)
7			(2 3 4/3)	(2 3 5/2)
8				(3/2 5/2 5)
9				(2 5/3 5)
10				(3 5/3 5/2), (3 5/4 5)
11			(2 3/2 4/3)	(2 3/2 5)
13				(2 3 5/3)
14			(3/2 4/3 4/3)	(3/2 5/2 5/2), (3 3 5/4)
16				(3 5/4 5/2)
17				(2 3/2 5/2)
18				(3/2 3 5/3), (5/3 5/3 5/2)
19				(2 3 5/4)
21				(2 5/4 5/2)
22				(3/2 3/2 5/2)
23				(2 3/2 5/3)
26				(3/2 5/3 5/3)
27				(2 5/4 5/3)
29				(2 3/2 5/4)
32				(3/2 5/4 5/3)
34				(3/2 3/2 5/4)
38				(3/2 5/4 5/4)
42				(5/4 5/4 5/4)

Även om en polyeder vanligtvis har samma densitet som Schwarz-triangeln den genereras från, är detta inte alltid fallet. För det första har polyedrar som har ansikten som passerar genom mitten av modellen (inklusive hemipolyedrarna, stora dirhombicosidodecahedron och stora disnub dirhombidodecahedron) inte en väldefinierad densitet. För det andra kan den distorsion som är nödvändig för att återställa likformighet vid byte av en sfärisk polyeder till dess plana motsvarighet trycka ytor genom mitten av polyedern och tillbaka ut på andra sidan, vilket ändrar densiteten. Detta händer i följande fall:

• Den stora stympade kuboktaedern , 2 3 4/3 |. Medan Schwarz-triangeln (2 3 4/3) har densitet 7, trycker återhämtande likformighet de åtta hexagonerna genom mitten, vilket ger densitet |7 − 8| = 1, samma som för den kolunära Schwarz-triangeln (2 3 4) som delar samma storcirklar.
• Den stympade dodecadodecahedron , 2 5/3 5 |. Medan Schwarz-triangeln (2 5/3 5) har densitet 9, trycker återhämtande enhetlighet de tolv dekagonerna genom mitten, vilket ger densitet |9 − 12| = 3, samma som för den kolunära Schwarz-triangeln (2 5/2 5) som delar samma storcirklar.
• Tre snubbiga polyedrar: den stora ikosaedern | 2 3/2 3/2, den lilla retrosnubben icosicosidodecahedron | 3/2 3/2 5/2, och den stora retrosnubben icosidodecahedron | 2 3/2 5/3. Här har vertexfigurerna förvrängts till pentagram eller hexagram snarare än pentagoner eller hexagoner, vilket skjuter alla snubbiga trianglar genom mitten och ger tätheter på |5 − 12| = 7, |22 − 60| = 38, och |23 − 60| = 37 respektive. Dessa tätheter är desamma som för kolarreflexvinklade Schwarz -trianglar som inte ingår ovan. Sålunda kan den stora icosahedronen anses komma från (2/3 3 3) eller (2 3 3/4), den lilla retrosnub icosicosidodecahedron från (3 3 5/8) eller (3 3/4 5/3), och den stora retrosnubben icosidodecahedron från (2/3 3 5/2), (2 3/4 5/3), eller (2 3 5/7). (Coxeter, "Uniform polyhedra", 1954)

Översiktstabell

De åtta formerna för Wythoff-konstruktionerna från en allmän triangel (pqr). Partiella snubbar kan också skapas (visas inte i den här artikeln).

De nio reflexibla formerna för Wythoff-konstruktionerna från en allmän fyrhörning (pqrs).

Det finns sju generatorpunkter med varje uppsättning p,q,r (och några speciella former):

Allmän				Rätt triangel (r=2)
Beskrivning	Wythoff symbol	Vertex- konfiguration	Coxeter diagram	Wythoff symbol	Vertex- konfiguration	Schläfli symbol	Coxeter diagram
regelbunden och kvasiregelbunden	q | pr	(pr) q		q | p 2	p q	{p,q}
	p | qr	(qr) sid		p | q 2	q sid	{q,p}
	r | pq	(qp) r		2 | pq	(qp) 2	t 1 {p,q}
trunkerade och utvidgade	qr | sid	q.2p.r.2p		q 2 | sid	q.2p.2p	t 0,1 {p,q}
	pr | q	p.2q.r.2q		p 2 | q	sid. 2q.2q	t 0,1 {q,p}
	pq | r	2r.q.2r.p		pq | 2	4.q.4.p	t 0,2 {p,q}
jämnt ansikte	pqr |	2r.2q.2p		pq 2 |	4.2q.2p	t 0,1,2 {p,q}
	pq r s |	2p.2q.-2p.-2q	-	p 2 r s |	2p.4.-2p. 4/3 _ _		-
nonchalera	| pqr	3.r.3.q.3.p		| pq 2	3.3.q.3.p	sr{p,q}
	| pqrs	(4.p.4.q.4.r.4.s)/2	-	-	-		-

Det finns fyra specialfall:

• pq
  ^r _s | – Det här är en blandning av pqr | och pqs | . Båda symbolerna pqr | och pqs | generera en gemensam baspolyeder med några extra ytor. Notationen pq
  ^r _s | representerar då baspolyedern, som består av de ytor som är gemensamma för båda pqr | och pqs | .
• | pqr – Snub-former (omväxlande) ges denna annars oanvända symbol.
• | pqrs – En unik snubbform för U75 som inte är Wythoff-konstruerbar med hjälp av triangulära fundamentala domäner. Fyra tal ingår i denna Wythoff-symbol eftersom denna polyeder har en tetragonal sfärisk fundamental domän.
• | (p) q (r) s – En unik snubbform för Skillings figur som inte är Wythoff-konstruerbar.

Denna omvandlingstabell från Wythoff-symbol till vertexkonfiguration misslyckas för de exceptionella fem polyedrarna som anges ovan vars densiteter inte matchar densiteterna för deras genererande Schwarz-triangel-tesselationer. I dessa fall är vertexfiguren kraftigt förvrängd för att uppnå enhetlighet med plana ytor: i de första två fallen är det en trubbig triangel istället för en spetsig triangel, och i de sista tre är det ett pentagram eller hexagram istället för en femkant eller hexagon, slingrande runt mitten två gånger. Detta resulterar i att vissa ytor skjuts rakt igenom polyedern jämfört med de topologiskt ekvivalenta formerna utan att vertexfiguren förvrängs och kommer ut retrograd på andra sidan.

I tabellerna nedan markerar röda bakgrunder degenererade polyedrar. Gröna bakgrunder markerar de konvexa enhetliga polyedrarna.

Dihedral (prismatisk)

I dihedriska Schwarz-trianglar är två av talen 2, och det tredje kan vara vilket rationellt tal som helst som är strikt större än 1.

1. (2 2 n / d ) – degenerera om gcd( n , d ) > 1.

Många av polyedrarna med dihedrisk symmetri har digon- ansikter som gör dem till degenererade polyedrar (t.ex. dihedra och hosohedra ). Tabellens kolumner som endast ger degenererade enhetliga polyedrar ingår inte: speciella degenererade fall (endast i (2 2 2) Schwarz-triangeln) är markerade med ett stort kors. Enhetliga korsade antiprismor med en bas { p } där p < 3/2 inte kan existera eftersom deras vertexfigurer skulle bryta mot den triangulära olikheten ; dessa är också markerade med ett stort kors. Den 3/2-korsade antiprisman (trirp) är degenererad, är platt i det euklidiska rymden och är också markerad med ett stort kors. Schwarz-trianglarna (2 2 n / d ) listas här endast när gcd( n , d ) = 1, eftersom de annars endast resulterar i degenererade likformiga polyedrar.

Listan nedan visar alla möjliga fall där n ≤ 6.

(p q r)	qr | p q.2p.r.2p	pr | q sid. 2q.r.2q	pqr | 2r.2q.2p	| pqr 3.r.3.q.3.p
(2 2 2) (μ=1)	X	X	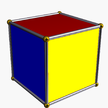4.4.4 kub 4-p	3.3.3 tet 2-ap
(2 2 3) (μ=1)	4.3.4 resa 3-s	4.3.4 resa 3-s	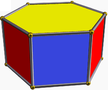6.4.4 höft 6-p	3.3.3.3 okt 3-ap
(2 2 3/2) (μ=2)	4.3.4 resa 3-s	4.3.4 resa 3-s	6/2.4.4 2trip 6/2-p	X
(2 2 4) (μ=1)	4.4.4 kub 4-p	4.4.4 kub 4-p	8.4.4 op 8-s	3.4.3.3 squap 4-ap
(2 2 4/3) (μ=3)	4.4.4 kub 4-p	4.4.4 kub 4-p	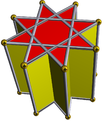8/3.4.4 stopp 8/3-p	X
(2 2 5) (μ=1)	4.5.4 pip 5-p	4.5.4 pip 5-p	10.4.4 dip 10-p	3.5.3.3 pap 5-ap
(2 2 5/2) (μ=2)	4,5/2,4 stip 5/2-p	4,5/2,4 stip 5/2-p	10/2.4.4 2pip 10/2-p	3.5/2.3.3 stap 5/2-ap
(2 2 5/3) (μ=3)	4,5/2,4 stip 5/2-p	4,5/2,4 stip 5/2-p	10/3.4.4 stiddip 10/3-p	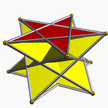3.5/3.3.3 stjärna 5/3-ap
(2 2 5/4) (μ=4)	4.5.4 pip 5-p	4.5.4 pip 5-p	10/4.4.4 2stip 10/4-p	X
(2 2 6) (μ=1)	4.6.4 höft 6-p	4.6.4 höft 6-p	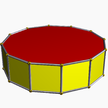12.4.4 twip 12-p	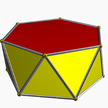3.6.3.3 hap 6-ap
(2 2 6/5) (μ=5)	4.6.4 höft 6-p	4.6.4 höft 6-p	12/5.4.4 stwip 12/5-p	X
(2 2 n ) (μ=1)	4. n .4 n -p	4. n .4 n -p	2 n .4.4 2 n -p	3. n .3.3 n -ap
(2 2 n / d ) (μ= d )	4. n / d .4 n / d -p	4. n / d .4 n / d -p	2 n / d .4.4 2 n / d -p	3. n / d .3.3 n / d -ap

Tetraedrisk

I tetraedriska Schwarz-trianglar är den högsta tillåtna täljaren 3.

#	(p q r)	q | pr (pr) q	p | qr (qr) sid	r | pq (qp) r	qr | p q.2p.r.2p	pr | q sid. 2q.r.2q	pq | r 2r.q.2r.p	pqr | 2r.2q.2p	| pqr 3.r.3.q.3.p
1	(3 3 2) (μ=1)	3.3.3 tet U1	3.3.3 tet U1	3.3.3.3 okt U5	3.6.6 tut U2	3.6.6 tut U2	4.3.4.3 co U7	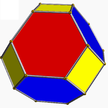4.6.6 toe U8	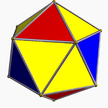3.3.3.3.3 som U22
2	(3 3 3/2) (μ=2)	(3.3.3.3.3.3)/2 2tet –	(3.3.3.3.3.3)/2 2tet –	(3.3.3.3.3.3)/2 2tet –	3.6.3/2.6 oho U3	3.6.3/2.6 oho U3	2(6/2.3.6/2.3) 2okt –	2(6/2.6.6) 2tut –	2(3.3/2.3.3.3.3) 2okt+8{3} –
3	(3 2 3/2) (μ=3)	3.3.3.3 okt U5	3.3.3 tet U1	3.3.3 tet U1	3.6.6 tut U2	2(3/2.4.3.4) 2thah U4*	3(3,6/2,6/2) 3tet –	2(6/2.4.6) cho+4{6/2} U15*	3(3.3.3) 3tet –
4	(2 3/2 3/2) (μ=5)	3.3.3 tet U1	3.3.3.3 okt U5	3.3.3 tet U1	3.4.3.4 co U7	3(6/2.3.6/2) 3tet –	3(6/2.3.6/2) 3tet –	4(6/2.6/2.4) 2okt+6{4} –	(3.3.3.3.3)/2 gike U53
5	(3/2 3/2 3/2) (μ=6)	(3.3.3.3.3.3)/2 2tet –	(3.3.3.3.3.3)/2 2tet –	(3.3.3.3.3.3)/2 2tet –	2(6/2.3.6/2.3) 2okt –	2(6/2.3.6/2.3) 2okt –	2(6/2.3.6/2.3) 2okt –	6(6/2.6/2.6/2) 6tet –	?

Octaedral

I oktaedriska Schwarz-trianglar är den maximala tillåtna täljaren 4. Det finns också oktaedriska Schwarz-trianglar som använder 4/2 som tal, men dessa leder bara till degenererade enhetliga polyedrar eftersom 4 och 2 har en gemensam faktor .

#	(p q r)	q | pr (pr) q	p | qr (qr) sid	r | pq (qp) r	qr | p q.2p.r.2p	pr | q sid. 2q.r.2q	pq | r 2r.q.2r.p	pqr | 2r.2q.2p	| pqr 3.r.3.q.3.p
1	(4 3 2) (μ=1)	4.4.4 kub U6	3.3.3.3 okt U5	3.4.3.4 co U7	3.8.8 tic U9	4.6.6 toe U8	4.3.4.4 sirco U10	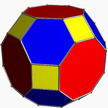4.6.8 girco U11	3.3.3.3.4 snic U12
2	(4 4 3/2) (μ=2)	(3/2.4) 4 okt+6{4} –	(3/2.4) 4 okt+6{4} –	(4.4.4.4.4.4)/2 2 kub –	3/2.8.4.8 socco U13	3/2.8.4.8 socco U13	2(6/2.4.6/2.4) 2co –	2(6/2.8.8) 2tic –	?
3	(4 3 4/3) (μ=4)	(4.4.4.4.4.4)/2 2 kub –	(3/2.4) 4 okt+6{4} –	(3/2.4) 4 okt+6{4} –	3/2.8.4.8 socco U13	2(4/3.6.4.6) 2cho U15*	3,8/3,4,8/3 gocco U14	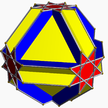6.8.8/3 cotco U16	?
4	(4 2 3/2) (μ=5)	3.4.3.4 co U7	3.3.3.3 okt U5	4.4.4 kub U6	3.8.8 tic U9	4.4.3/2.4 querco U17	4(4.6/2.6/2) 2okt+6{4} –	2(4,6/2,8) sroh+8{6/2} U18*	?
5	(3 2 4/3) (μ=7)	3.4.3.4 co U7	4.4.4 kub U6	3.3.3.3 okt U5	4.6.6 toe U8	4.4.3/2.4 querco U17	3,8/3,8/3 slutade U19	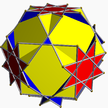4,6/5,8/3 quitco U20	?
6	(2 3/2 4/3) (μ=11)	4.4.4 kub U6	3.4.3.4 co U7	3.3.3.3 okt U5	4.3.4.4 sirco U10	4(4.6/2.6/2) 2okt+6{4} –	3,8/3,8/3 slutade U19	2(4,6/2,8/3) groh+8{6/2} U21*	?
7	(3/2 4/3 4/3) (μ=14)	(3/2.4) 4 = (3.4) 4 /3 okt+6{4} –	(4.4.4.4.4.4)/2 2 kub –	(3/2.4) 4 = (3.4) 4 /3 okt+6{4} –	2(6/2.4.6/2.4) 2co –	3,8/3,4,8/3 gocco U14	3,8/3,4,8/3 gocco U14	2(6/2,8/3,8/3) 2quith –	?

Icosahedral

I icosaedriska Schwarz-trianglar är den maximala tillåtna täljaren 5. Dessutom kan täljaren 4 inte användas alls i icosahedriska Schwarz-trianglar, även om täljare 2 och 3 är tillåtna. (Om 4 och 5 kunde förekomma tillsammans i någon Schwarz-triangel, skulle de också behöva göra det i någon Möbius-triangel, men detta är omöjligt eftersom (2 4 5) är en hyperbolisk triangel, inte en sfärisk.)

#	(p q r)	q | pr (pr) q	p | qr (qr) sid	r | pq (qp) r	qr | p q.2p.r.2p	pr | q sid. 2q.r.2q	pq | r 2r.q.2r.p	pqr | 2r.2q.2p	| pqr 3.r.3.q.3.p
1	(5 3 2) (μ=1)	5.5.5 doe U23	3.3.3.3.3 som U22	3.5.3.5 id U24	3.10.10 tid U26	5.6.6 ti U25	4.3.4.5 srid U27	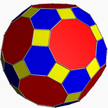4.6.10 rutnät U28	3.3.3.3.5 snid U29
2	(3 3 5/2) (μ=2)	3,5/2,3,5/2,3,5/2 sidtid U30	3,5/2,3,5/2,3,5/2 sidtid U30	(3 10 )/2 2like –	3.6.5/2.6 siid U31	3.6.5/2.6 siid U31	2(10/2.3.10/2.3) 2id –	2(10/2.6.6) 2ti –	3.5/2.3.3.3.3 seside U32
3	(5 5 3/2) (μ=2)	(5.3/2) 5 cid –	(5.3/2) 5 cid –	(5.5.5.5.5.5)/2 2doe –	5.10.3/2.10 trist U33	5.10.3/2.10 trist U33	2(6/2.5.6/2.5) 2id –	2(6/2.10.10) 2tid –	2(3.3/2.3.5.3.5) 2id+40{3} –
4	(5 5/2 2) (μ=3)	(5.5.5.5.5)/2 gad U35	5/2,5/2,5/2,5/2,5/2 sissid U34	5/2,5,5/2,5 gjorde U36	5/2.10.10 tigid U37	5.10/2.10/2 3doe –	4,5/2,4,5 radad U38	2(4.10/2.10) sird+12{10/2} U39*	3.3.5/2.3.5 siddid U40
5	(5 3 5/3) (μ=4)	5,5/3,5,5/3,5,5/3 ditdid U41	(3,5/3) 5 gacid –	(3,5 ) 5/3 cid –	3.10.5/3.10 sidditdid U43	5.6.5/3.6 id U44	10/3.3.10/3.5 gidditdid U42	10/3.6.10 idtid U45	3.5/3.3.3.3.5 sidig U46
6	(5/2 5/2 5/2) (μ=6)	(5/2) 10 /2 2sissid –	(5/2) 10 /2 2sissid –	(5/2) 10 /2 2sissid –	2(5/2.10/2) 2 2 gjorde –	2(5/2.10/2) 2 2 gjorde –	2(5/2.10/2) 2 2 gjorde –	6(10/2.10/2.10/2) 6doe –	3(3.5/2.3.5/2.3.5/2) 3sidtid –
7	(5 3 3/2) (μ=6)	(3.5.3.5.3.5)/2 gidtid U47	(3 10 )/4 2 gike –	(3.5.3.5.3.5)/2 gidtid U47	2(3.10.3/2.10) 2seihid U49*	5.6.3/2.6 giid U48	5(6/2.3.6/2.5) 3ike+gad –	2(6.6/2.10) siddy+20{6/2} U50*	5(3.3.3.3.3.5)/2 5ike+gad –
8	(5 5 5/4) (μ=6)	(5 10 )/4 2gad –	(5 10 )/4 2gad –	(5 10 )/4 2gad –	2(5.10.5/4.10) 2sidhid U51*	2(5.10.5/4.10) 2sidhid U51*	10/4.5.10/4.5 2did –	2(10/4.10.10) 2tigid –	3(3.5.3.5.3.5) 3cid –
9	(3 5/2 2) (μ=7)	(3.3.3.3.3)/2 gike U53	5/2,5/2,5/2 gissid U52	5/2.3.5/2.3 gid U54	5/2.6.6 tiggy U55	3.10/2.10/2 2gad+ike –	3(4.5/2.4.3) sicdatrid –	4.10/2.6 ri+12{10/2} U56*	3.3.5/2.3.3 gosid U57
10	(5 5/2 3/2) (μ=8)	(5.3/2) 5 cid –	(5/3.3) 5 gacid –	5,5/3,5,5/3,5,5/3 ditdid U41	5/3.10.3.10 sidditdid U43	5(5.10/2.3.10/2) ike+3gad –	3(6/2,5/2,6/2,5) sidtid+gidtid –	4(6/2.10/2.10) id+seihid+sidhid –	? (3|3 5/2) + (3/2|3 5)
11	(5 2 5/3) (μ=9)	5,5/2,5,5/2 gjorde U36	5/2,5/2,5/2,5/2,5/2 sissid U34	(5.5.5.5.5)/2 gad U35	5/2.10.10 tigid U37	3(5.4.5/3.4) cadditradid –	10/3.5.5 sluta sissid U58	10/3.4.10/9 slutade U59	3.5/3.3.3.5 isdid U60
12	(3 5/2 5/3) (μ=10)	(3,5/3) 5 gacid –	(5/2 ) 6/2 2gissid –	(5/2.3 ) 5/3 gacid –	2(5/2.6.5/3.6) 2sidhei U62*	3(3.10/2.5/3.10/2) ditdid+gidtid –	10/3,5/2,10/3,3 gaddid U61	10/3.10/2.6 snurrig+12{10/2} U63*	3.5/3.3.5/2.3.3 gisdid U64
13	(5 3 5/4) (μ=10)	(5.5.5.5.5.5)/2 2doe –	(3/2,5) 5 cid –	(3,5 ) 5/3 cid –	3/2.10.5.10 trist U33	2(5.6.5/4.6) 2gidhei U65*	3(10/4.3.10/4.5) sidtid+ditdid –	2(10/4.6.10) siddy+12{10/4} U50*	?
14	(5 2 3/2) (μ=11)	5.3.5.3 id U24	3.3.3.3.3 som U22	5.5.5 doe U23	3.10.10 tid U26	3(5/4.4.3/2.4) gicdatrid –	5(5,6/2,6/2) 2ike+gad –	2(6/2.4.10) sird+20{6/2} U39*	5(3.3.3.5.3)/2 4ike+gad –
15	(3 2 5/3) (μ=13)	3,5/2,3,5/2 gid U54	5/2,5/2,5/2 gissid U52	(3.3.3.3.3)/2 gike U53	5/2.6.6 tiggy U55	3.4.5/3.4 qrid U67	10/3.10/3.3 slutar gissid U66	10/3.4.6 gaquatid U68	3.5/3.3.3.3 gisid U69
16	(5/2 5/2 3/2) (μ=14)	(5/3.3) 5 gacid –	(5/3.3) 5 gacid –	(5/2 ) 6/2 2gissid –	3(5/3.10/2.3.10/2) ditdid+gidtid –	3(5/3.10/2.3.10/2) ditdid+gidtid –	2(6/2.5/2.6/2.5/2) 2gid –	10(6/2.10/2.10/2) 2ike+4gad –	?
17	(3 3 5/4) (μ=14)	(3.5.3.5.3.5)/2 gidtid U47	(3.5.3.5.3.5)/2 gidtid U47	(3) 10 /4 2gike –	3/2.6.5.6 giid U48	3/2.6.5.6 giid U48	2(10/4.3.10/4.3) 2gid –	2(10/4.6.6) 2tiggy –	?
18	(3 5/2 5/4) (μ=16)	(3/2,5) 5 cid –	5/3.5.5/3.5.5/3.5 ditdid U41	(5/2.3 ) 5/3 gacid –	5/3.6.5.6 ided U44	5(3/2.10/2.5.10/2) ike+3gad –	5(10/4.5/2.10/4.3) 3sissid+gike –	4(10/4.10/2.6) did+sidhei+gidhei –	?
19	(5/2 2 3/2) (μ=17)	3,5/2,3,5/2 gid U54	(3.3.3.3.3)/2 gike U53	5/2,5/2,5/2 gissid U52	5(10/2.3.10/2) 2gad+ike –	5/3.4.3.4 qrid U67	5(6/2.6/2.5/2) 2gike+sissid –	6(6/2.4.10/2) 2gidtid+rhom –	?
20	(5/2 5/3 5/3) (μ=18)	(5/2) 10 /2 2sissid –	(5/2) 10 /2 2sissid –	(5/2) 10 /2 2sissid –	2(5/2.10/2) 2 2 gjorde –	2(5/2.10/3.5/3.10/3) 2gidhid U70*	2(5/2.10/3.5/3.10/3) 2gidhid U70*	2(10/3.10/3.10/2) 2quitsissid –	?
21	(3 5/3 3/2) (μ=18)	(3 10 )/2 2like –	5/2.3.5/2.3.5/2.3 sidtid U30	5/2.3.5/2.3.5/2.3 sidtid U30	5/2.6.3.6 siid U31	2(3.10/3.3/2.10/3) 2geihid U71*	5(6/2.5/3.6/2.3) sissid+3gike –	2(6/2.10/3.6) snurrig+20{6/2} U63*	?
22	(3 2 5/4) (μ=19)	3.5.3.5 id U24	5.5.5 doe U23	3.3.3.3.3 som U22	5.6.6 ti U25	3(3/2.4.5/4.4) gicdatrid –	5(10/4.10/4.3) 2sissid+gike –	2(10/4.4.6) ri+12{10/4} U56*	?
23	(5/2 2 5/4) (μ=21)	5/2,5,5/2,5 gjorde U36	(5.5.5.5.5)/2 gad U35	5/2,5/2,5/2,5/2,5/2 sissid U34	3(10/2.5.10/2) 3doe –	3(5/3.4.5.4) cadditradid –	3(10/4.5/2.10/4) 3gissid –	6(10/4.4.10/2) 2ditdid+rhom –	?
24	(5/2 3/2 3/2) (μ=22)	5/2.3.5/2.3.5/2.3 sidtid U30	(3 10 )/2 2like –	5/2.3.5/2.3.5/2.3 sidtid U30	2(3.10/2.3.10/2) 2id –	5(5/3.6/2.3.6/2) sissid+3gike –	5(5/3.6/2.3.6/2) sissid+3gike –	10(6/2.6/2.10/2) 4ike+2gad –	(3.3.3.3.3.5/2)/2 sirsid U72
25	(2 5/3 3/2) (μ=23)	(3.3.3.3.3)/2 gike U53	5/2.3.5/2.3 gid U54	5/2,5/2,5/2 gissid U52	3(5/2.4.3.4) sicdatrid –	10/3.3.10/3 slutar gissid U66	5(6/2.5/2.6/2) 2gike+sissid –	2(6/2.10/3.4) band+20{6/2} U73*	(3.3.3.5/2.3)/2 girsid U74
26	(5/3 5/3 3/2) (μ=26)	(5/2.3 ) 5/3 gacid –	(5/2.3 ) 5/3 gacid –	(5/2 ) 6/2 2gissid –	5/2.10/3.3.10/3 gaddid U61	5/2.10/3.3.10/3 gaddid U61	2(6/2.5/2.6/2.5/2) 2gid –	2(6/2.10/3.10/3) 2quitgissid –	?
27	(2 5/3 5/4) (μ=27)	(5.5.5.5.5)/2 gad U35	5/2,5,5/2,5 gjorde U36	5/2,5/2,5/2,5/2,5/2 sissid U34	5/2.4.5.4 radad U38	10/3.5.10/3 slutade sissid U58	3(10/4.5/2.10/4) 3gissid –	2(10/4.10/3.4) band+12{10/4} U73*	?
28	(2 3/2 5/4) (μ=29)	5.5.5 doe U23	3.5.3.5 id U24	3.3.3.3.3 som U22	3.4.5.4 srid U27	2(6/2.5.6/2) 2ike+gad –	5(10/4.3.10/4) 2sissid+gike –	6(10/4.6/2.4/3) 2sidtid+rhom –	?
29	(5/3 3/2 5/4) (μ=32)	5/3.5.5/3.5.5/3.5 ditdid U41	(3,5 ) 5/3 cid –	(3,5/2 ) 5/3 gacid –	3.10/3.5.10/3 gidditdid U42	3(5/2.6/2.5.6/2) sidtid+gidtid –	5(10/4.3.10/4.5/2) 3sissid+gike –	4(10/4.6/2.10/3) gid+geihid+gidhid –	?
30	(3/2 3/2 5/4) (μ=34)	(3.5.3.5.3.5)/2 gidtid U47	(3.5.3.5.3.5)/2 gidtid U47	(3) 10 /4 2gike –	5(3.6/2.5.6/2) 3ike+gad –	5(3.6/2.5.6/2) 3ike+gad –	2(10/4.3.10/4.3) 2gid –	10(10/4.6/2.6/2) 2sissid+4gike –	?
31	(3/2 5/4 5/4) (μ=38)	(3,5 ) 5/3 cid –	(5.5.5.5.5.5)/2 2doe –	(3,5 ) 5/3 cid –	2(5.6/2.5.6/2) 2id –	3(3.10/4.5/4.10/4) sidtid+ditdid –	3(3.10/4.5/4.10/4) sidtid+ditdid –	10(10/4.10/4.6/2) 4sissid+2gike –	5(3.3.3.5/4.3.5/4) 4ike+2gad –
32	(5/4 5/4 5/4) (μ=42)	(5) 10 /4 2gad –	(5) 10 /4 2gad –	(5) 10 /4 2gad –	2(5.10/4.5.10/4) 2did –	2(5.10/4.5.10/4) 2did –	2(5.10/4.5.10/4) 2did –	6(10/4.10/4.10/4) 2gissid –	3(3/2.5.3/2.5.3/2.5) 3cid –

Icke-Wythoffian

Hemi former

Bortsett från oktahemioktaedern genereras hemipolyedrarna som dubbla beläggningar av Wythoff- konstruktionen .

3/2.4.3.4 thah U4 hemi(3 3/2 | 2)	4/3.6.4.6 cho U15 hemi(4 4/3 | 3)	5/4.10.5.10 sidhid U51 hemi(5 5/4 | 5)	5/2.6.5/3.6 sidhei U62 hemi(5/2 5/3 | 3)	5/2.10/3.5/3.10/3 gidhid U70 hemi(5/2 5/3 | 5/3)
	3/2.6.3.6 oho U3 hemi(?)	3/2.10.3.10 seihid U49 hemi(3 3/2 | 5)	5.6.5/4.6 gidhei U65 hemi(5 5/4 | 3)	3.10/3.3/2.10/3 geihid U71 hemi(3 3/2 | 5/3)

Reducerade former

Dessa polyedrar genereras med extra ytor av Wythoff-konstruktionen.

Wythoff	Polyeder	Extra ansikten		Wythoff	Polyeder	Extra ansikten		Wythoff	Polyeder	Extra ansikten
3 2 3/2 |	4.6.4/3.6 cho U15	4{6/2}		4 2 3/2 |	4.8.4/3.8/7 sroh U18	8{6/2}		2 3/2 4/3 |	4,8/3,4/3,8/5 groh U21	8{6/2}
5 5/2 2 |	4.10.4/3.10/9 sird U39	12{10/2}		5 3 3/2 |	10.6.10/9.6/5 siddy U50	20{6/2}		3 5/2 2 |	6.4.6/5.4/3 ri U56	12{10/2}
5 5/2 3/2 |	3/2.10.3.10 seihid U49	id + sidhid		5 5/2 3/2 |	5/4.10.5.10 sidhid U51	id + seihid		5 3 5/4 |	10.6.10/9.6/5 siddy U50	12{10/4}
3 5/2 5/3 |	6.10/3.6/5.10/7 snurrig U63	12{10/2}		5 2 3/2 |	4.10/3.4/3.10/9 sird U39	20{6/2}		3 5/2 5/4 |	5.6.5/4.6 gidhei U65	gjorde + sidhei
3 5/2 5/4 |	5/2.6.5/3.6 sidhei U62	gjorde + gidhei		3 5/3 3/2 |	6.10/3.6/5.10/7 snurrig U63	20{6/2}		3 2 5/4 |	6.4.6/5.4/3 ri U56	12{10/4}
2 5/3 3/2 |	4,10/3,4/3,10/7 gjord U73	20{6/2}		5/3 3/2 5/4 |	3.10/3.3/2.10/3 geihid U71	gid + gidhid		5/3 3/2 5/4 |	5/2.10/3.5/3.10/3 gidhid U70	gid + geihid
2 5/3 5/4 |	4,10/3,4/3,10/7 gjord U73	12{10/4}

Tetrahemihexaedern (thah, U4) är också en reducerad version av {3/2}- kupolen (retrograd triangulär kupol, ratricu ) med {6/2}. Som sådan kan den också kallas den korsade triangulära kuploiden .

Många fall ovan härrör från degenererade omnitrunkerade polyedrar pqr |. I dessa fall, två distinkta degenererade fall pqr | och pqs | kan genereras från samma p och q; resultatet har ansikten {2p}, {2q} och sammanfallande {2r} respektive {2s}. Dessa båda ger samma icke degenererade enhetliga polyedrar när de sammanfallande ytorna kasseras, vilket Coxeter symboliserade pq
^r _s |. Dessa fall listas nedan:

4.6.4/3.6 cho U15 2 3 3/2 3/2 |	4.8.4/3.8/7 sroh U18 2 3 3/2 4/2 |	4.10.4/3.10/9 sird U39 2 3 3/2 5/2 |	6.10/3.6/5.10/7 snurrig U63 3 5/3 3/2 5/2 |
6.4.6/5.4/3 ri U56 2 3 5/4 5/2 |	4,8/3,4/3,8/5 groh U21 2 4/3 3/2 4/2 |	4.10/3.4/3.10/7 gjord U73 2 5/3 3/2 5/4 |	10.6.10/9.6/5 siddy U50 3 5 3/2 5/4 |

I den lilla och stora rhombihexaedran används fraktionen 4/2 trots att den inte är i lägsta termer. Medan 2 4 2 | och 2 4/3 2 | representerar ett enda åttkantigt respektive åttagrammiskt prisma, 2 4 4/2 | och 2 4/3 4/2 | representerar tre sådana prismor, som delar några av sina fyrkantiga ytor (exakt de som är dubblerade för att producera {8/2}). Dessa {8/2} visas med fyrfaldig och inte tvåfaldig rotationssymmetri, vilket motiverar användningen av 4/2 istället för 2.

Andra former

Dessa två enhetliga polyedrar kan inte genereras alls av Wythoff-konstruktionen. Detta är uppsättningen av enhetliga polyedrar som vanligtvis beskrivs som "icke-Wythoffians". Istället för de triangulära fundamentala domänerna i Wythoffs enhetliga polyedrar har dessa två polyedrar tetragonala fundamentala domäner.

Skillings figur ges inget index i Maeders lista på grund av att det är en exotisk enhetlig polyeder, med åsar (kanter i 3D-fallet) helt sammanfallande. Detta är också sant för en del av de degenererade polyedern som ingår i listan ovan, såsom den lilla komplexa icosidodecahedron . Denna tolkning av att kanter är sammanfallande tillåter att dessa figurer har två ytor per kant: att inte dubbla kanterna skulle ge dem 4, 6, 8, 10 eller 12 ytor som möts vid en kant, figurer som vanligtvis utesluts som enhetliga polyedrar. Skillings figur har 4 ansikten som möts vid vissa kanter.

(pqrs)	| pqrs (4.p. 4.q.4.r.4.s)/2	| (p) q (r) s (p 3 .4.q.4.r 3 .4.s.4)/2
(3/2 5/3 3 5/2)	(4.3/2.4.5/3.4.3.4.5/2)/2 gidrid U75	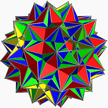(3/2 3 .4.5/3.4.3 3 .4.5/2.4)/2 gidisdrid Skilling

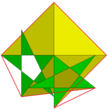Vertex figur av | 3 5/3 5/2	Stor snubbig dodecicosidodecahedron	Stor dirhombicosidodecahedron	Vertex figur av | 3/2 5/3 3 5/2
Stor disnub dirhombidodecahedron	Sammansättning av tjugo oktaedrar	Förening av tjugo tetrahemihexaedrar	Hörnet av |(3/2) 5/3 (3) 5/2

Båda dessa speciella polyedrar kan härledas från den stora snubben dodecicosidodecahedron , | 3 5/3 5/2 (U64). Detta är en kiral snubbpolyeder, men dess pentagram visas i par i samma plan. Genom att kombinera en kopia av denna polyeder med dess enantiomorf, sammanfaller pentagrammen och kan tas bort. Eftersom kanterna på denna polyeders vertexfigur inkluderar tre sidor av en kvadrat, där den fjärde sidan bidrar med sin enantiomorf, ser vi att den resulterande polyedern i själva verket är sammansättningen av tjugo oktaedrar . Var och en av dessa oktaedrar innehåller ett par parallella ytor som härrör från en helt symmetrisk triangel av | 3 5/3 5/2, medan de andra tre kommer från originalet | 3 5/3 5/2:s snubbiga trianglar. Dessutom kan varje oktaeder ersättas av tetrahemihexaedern med samma kanter och hörn. Om man tar de helt symmetriska trianglarna i oktaedrarna, de ursprungliga sammanfallande pentagrammen i den stora snubben dodecicosidodecahedra, och de ekvatoriala kvadraterna på tetrahemihexaedran tillsammans ger den stora dirhombicosidodecahedronen (Millers monster). Genom att ta oktaedrarnas snubbiga trianglar istället får man den stora disnub dirhombidodecahedronen (Skillings figur).

Euklidiska plattsättningar

De enda plana trianglarna som plattar planet en gång över är (3 3 3), (4 2 4) och (3 2 6): de är den liksidiga triangeln, den 45-45-90 rätt likbenta triangeln och 30 -60-90 rät triangel. Därav följer att alla plan triangel som lägger plattor på planet flera gånger måste byggas upp från flera kopior av en av dessa. Den enda möjligheten är att den 30-30-120 trubbiga likbenta triangeln (3/2 6 6) = (6 2 3) + (2 6 3) lägger planet två gånger. Varje triangel räknas två gånger med motsatt orientering, med en förgreningspunkt vid 120° hörn.

Kakelsättningen {∞,2} gjord av två apeirogoner accepteras inte, eftersom dess ytor möts vid mer än en kant. Här betecknar ∞' den retrograda motsvarigheten till ∞.

De degenererade namngivna formerna är:

• chatit: sammansättning av 3 hexagonala plattsättningar + triangulär plattsättning
• chata: sammansättning av 3 hexagonala plattsättningar + triangulär plattsättning + dubbla omslag av apeirogoner längs alla kantsekvenser
• cha: sammansättning av 3 hexagonala plattor + dubbla omslag av apeirogoner längs alla kantsekvenser
• cosa: kvadratisk plattsättning + dubbla omslag av apeirogoner längs alla kantsekvenser

(p q r)	q | pr (pr) q	p | qr (qr) sid	r | pq (qp) r	qr | p q.2p.r.2p	pr | q p.2q.r.2q	pq | r 2r.q.2r.p	pqr | 2r.2q.2p	| pqr 3.r.3.q.3.p
(6 3 2)	6.6.6 hexat	3.3.3.3.3.3 trat	3.6.3.6 att	3.12.12 toxat	6.6.6 hexat	4.3.4.6 srotat	4.6.12 grothat	3.3.3.3.6 snathat
(4 4 2)	4.4.4.4 knäböj	4.4.4.4 knäböj	4.4.4.4 knäböj	4.8.8 tosquat	4.8.8 tosquat	4.4.4.4 knäböj	4.8.8 tosquat	3.3.4.3.4 snask
(3 3 3)	3.3.3.3.3.3 trat	3.3.3.3.3.3 trat	3.3.3.3.3.3 trat	3.6.3.6 att	3.6.3.6 att	3.6.3.6 att	6.6.6 hexat	3.3.3.3.3.3 trat
(∞ 2 2)	—	—	—	—	4.4.∞ azip	4.4.∞ azip	4.4.∞ azip	3.3.3.∞ azap
(3/2 3/2 3)	3.3.3.3.3.3 trat	3.3.3.3.3.3 trat	3.3.3.3.3.3 trat	∞-täckt {3}	∞-täckt {3}	3.6.3.6 att	[degenererad]	?
(4 4/3 2)	4.4.4.4 knäböj	4.4.4.4 knäböj	4.4.4.4 knäböj	4.8.8 tosquat	4,8/5,8/5 quitsquat	∞-täckt {4}	4,8/3,8/7 qrasquit	?
(4/3 4/3 2)	4.4.4.4 knäböj	4.4.4.4 knäböj	4.4.4.4 knäböj	4,8/5,8/5 quitsquat	4,8/5,8/5 quitsquat	4.4.4.4 knäböj	4,8/5,8/5 quitsquat	3.3.4/3.3.4/3 rasisquat
(3/2 6 2)	3.3.3.3.3.3 trat	6.6.6 hexat	3.6.3.6 att	[degenererad]	3.12.12 toxat	3/2.4.6/5.4 qrothat	[degenererad]	?
(3 6/5 2)	3.3.3.3.3.3 trat	6.6.6 hexat	3.6.3.6 att	6.6.6 hexat	3/2.12/5.12/5 kvot	3/2.4.6/5.4 qrothat	4,6/5,12/5 slut	?
(3/2 6/5 2)	3.3.3.3.3.3 trat	6.6.6 hexat	3.6.3.6 att	[degenererad]	3/2.12/5.12/5 kvot	3.4.6.4 srotat	[degenererad]	?
(3/2 6 6)	(3/2.6) 6 chatit	(6.6.6.6.6.6)/2 2 hexat	(3/2.6) 6 chatit	[degenererad]	3/2.12.6.12 sköt att	3/2.12.6.12 sköt att	[degenererad]	?
(3 6 6/5)	(3/2.6) 6 chatit	(6.6.6.6.6.6)/2 2 hexat	(3/2.6) 6 chatit	∞-täckt {6}	3/2.12.6.12 sköt att	3.12/5.6/5.12/5 ghothat	6.12/5.12/11 thotithit	?
(3/2 6/5 6/5)	(3/2.6) 6 chatit	(6.6.6.6.6.6)/2 2 hexat	(3/2.6) 6 chatit	[degenererad]	3.12/5.6/5.12/5 ghothat	3.12/5.6/5.12/5 ghothat	[degenererad]	?
(3 3/2 ∞)	(3.∞) 3 /2 = (3/2.∞) 3 ditatha	(3.∞) 3 /2 = (3/2.∞) 3 ditatha	—	6.3/2.6.∞ chata	[degenererad]	3.∞.3/2.∞ tha	[degenererad]	?
(3 3 ∞')	(3.∞) 3 /2 = (3/2.∞) 3 ditatha	(3.∞) 3 /2 = (3/2.∞) 3 ditatha	—	6.3/2.6.∞ chata	6.3/2.6.∞ chata	[degenererad]	[degenererad]	?
(3/2 3/2 ∞')	(3.∞) 3 /2 = (3/2.∞) 3 ditatha	(3.∞) 3 /2 = (3/2.∞) 3 ditatha	—	[degenererad]	[degenererad]	[degenererad]	[degenererad]	?
(4 4/3 ∞)	(4.∞) 4 /3 cosa	(4.∞) 4 /3 cosa	—	8.4/3.8.∞ gossa	8/3.4.8/3.∞ sossa	4.∞.4/3.∞ sha	8.8/3.∞ satsa	3.4.3.4/3.3.∞ snassa
(4 4 ∞')	(4.∞) 4 /3 cosa	(4.∞) 4 /3 cosa	—	8.4/3.8.∞ gossa	8.4/3.8.∞ gossa	[degenererad]	[degenererad]	?
(4/3 4/3 ∞')	(4.∞) 4 /3 cosa	(4.∞) 4 /3 cosa	—	8/3.4.8/3.∞ sossa	8/3.4.8/3.∞ sossa	[degenererad]	[degenererad]	?
(6 6/5 ∞)	(6.∞) 6 /5 kap	(6.∞) 6 /5 kap	—	6/5.12.∞.12 ghaha	6.12/5.∞.12/5 shaha	6.∞.6/5.∞ 2hoha	12.12/5.∞ hatha	?
(6 6 ∞')	(6.∞) 6 /5 kap	(6.∞) 6 /5 kap	—	6/5.12.∞.12 ghaha	6/5.12.∞.12 ghaha	[degenererad]	[degenererad]	?
(6/5 6/5 ∞')	(6.∞) 6 /5 kap	(6.∞) 6 /5 kap	—	6.12/5.∞.12/5 shaha	6.12/5.∞.12/5 shaha	[degenererad]	[degenererad]	?

Kakelsättningen 6 6/5 | ∞ genereras som ett dubbelt hölje av Wythoffs konstruktion:

6.∞.6/5.∞ hoha hemi(6 6/5 | ∞)

Det finns också några plattsättningar med den blandade symbolen pq
^r _s |:

4.12.4/3.12/11 sraht 2 6 3/2 3 |

4.12/5.4/3.12/7 graht 2 6/5 3/2 3 |

8/3.8.8/5.8/7 sost 4/3 4 2 ∞ |

12/5.12.12/7.12/11 huht 6/5 6 3 ∞ |

Det finns också några icke-wythoffska kakelplattor:

3.3.3.4.4 etrat

3.3.3.4/3.4/3 retat

Uppsättningen av enhetliga plattsättningar av planet har inte visat sig vara komplett, till skillnad från uppsättningen av enhetliga polyedrar. Kakelsättningarna ovan representerar alla som hittats av Coxeter, Longuet-Higgins och Miller i deras 1954 papper om enhetliga polyedrar. De förmodade att listorna var fullständiga: detta bevisades av Sopov 1970 för de enhetliga polyedrarna, men har inte bevisats för de enhetliga plattsättningarna. Branko Grünbaum , JCP Miller och GC Shephard listar faktiskt femton fler icke-Wythoffian uniformer i Uniform Tilings with Hollow Tiles (1981):

4.8.8/3.4/3.∞ rorisassa	4.8/3.8.4/3.∞ rosassa	4.8.4/3.8.4/3.∞ rarsisresa (2 former)	4.8/3.4.8/3.4/3.∞ rassersa (2 former)
3/2.∞.3/2.∞.3/2.4.4	3/2.∞.3/2.∞.3/2.4/3.4/3
3/2.∞.3/2.∞.3/2.12/5.6.12/5	3/2.∞.3/2.∞.3/2.12/7.6/5.12/7	3/2.∞.3/2.∞.3/2.12.6/5.12	3/2.∞.3/2.∞.3/2.12/11.6/5.12/11	3/2.∞.3/2.4/3.4/3.3/2.4/3.4/3	3/2.∞.3/2.4.4.3/2.4.4
3/2.∞.3/2.4.4.3/2.4/3.4/3

Det finns två plattsättningar vardera för vertexfigurerna 4.8.4/3.8.4/3.∞ och 4.8/3.4.8/3.4/3.∞; de använder samma uppsättningar av hörn och kanter, men har en annan uppsättning kvadrater. Det finns också en tredje sida för var och en av dessa två vertexfigurer som bara är pseudo-uniform (alla hörn ser likadana ut, men de kommer i två symmetriomlopp). Därför, för euklidiska plattsättningar, bestämmer inte vertexkonfigurationen unikt plattsättningen. På bilderna nedan är de medföljande rutorna med horisontella och vertikala kanter markerade med en mittpunkt. En enskild ruta har kanter markerade.

• 

  Uniform ( tapetgrupp p4m)

• 

  Uniform (bakgrundsgrupp p4g)

• 

  Pseudo-uniform

Grünbaum, Miller och Shephard listar också 33 enhetliga plattsättningar som använder sicksack (skeva apeirogoner) som ansikten, varav tio är familjer som har en fri parameter (vinkeln på sicksacken). I åtta fall är denna parameter kontinuerlig; i två är det diskret.

Hyperboliska plattor

Uppsättningen av trianglar som täcker det hyperboliska planet är oändlig. Dessutom i hyperboliskt rymden behöver inte den fundamentala domänen vara en simplex. Följaktligen kan en fullständig lista över de likformiga plattsättningarna i det hyperboliska planet inte ges.

Även när det är begränsat till konvexa brickor, är det möjligt att hitta flera plattsättningar med samma vertexkonfiguration: se till exempel Snub order-6 square tiling#Relaterade polyedrar och tiling .

Några små konvexa fall (som inte involverar idealiska ansikten eller hörn) har angetts nedan:

(p q r)	q | pr (pr) q	p | qr (qr) sid	r | pq (qp) r	qr | p q.2p.r.2p	pr | q p.2q.r.2q	pq | r 2r.q.2r.p	pqr | 2r.2q.2p	| pqr 3.r.3.q.3.p
(7 3 2)	7.7.7 värme	3.3.3.3.3.3.3 hetrat	3.7.3.7 thet	3.14.14 theat	6.6.7 thetrat	4.3.4.7 srothet	4.6.14 grothet	3.3.3.3.7 snathet
(8 3 2)	8.8.8 okat	3.3.3.3.3.3.3.3 otrat	3.8.3.8 toct	3.16.16 tocat	6.6.8 totrat	4.3.4.8 srotoct	4.6.16 grotoct	3.3.3.3.8 snatokt
(5 4 2)	5.5.5.5 torv	4.4.4.4.4 pesquat	4.5.4.5 tepet	4.10.10 topeat	5.8.8 topesquat	4.4.4.5 srotepet	4.8.10 grotepet	3.3.4.3.5 steg
(6 4 2)	6.6.6.6 shexat	4.4.4.4.4.4 hisquat	4.6.4.6 det	4.12.12 toshexat	6.8.8 dettaquat	4.4.4.6 srotehat	4.8.12 grotehat	3.3.4.3.6 snatehat
(5 5 2)	5.5.5.5.5 pepat	5.5.5.5.5 pepat	5.5.5.5 torv	5.10.10 topepat	5.10.10 topepat	4.5.4.5 tepet	4.10.10 topeat	3.3.5.3.5 speat
(6 6 2)	6.6.6.6.6.6 hihat	6.6.6.6.6.6 hihat	6.6.6.6 shexat	6.12.12 detta	6.12.12 detta	4.6.4.6 det	4.12.12 toshexat	3.3.6.3.6 shihat
(4 3 3)	3.4.3.4.3.4 dittitecat	3.3.3.3.3.3.3.3 otrat	3.4.3.4.3.4 dittitecat	3.8.3.8 toct	6.3.6.4 sittitetrat	6.3.6.4 sittitetrat	6.6.8 totrat	3.3.3.3.3.4 staditet
(4 4 3)	3.4.3.4.3.4.3.4 ditetetrat	3.4.3.4.3.4.3.4 ditetetrat	4.4.4.4.4.4 hisquat	4.8.3.8 sittiteteat	4.8.3.8 sittiteteat	6.4.6.4 det	6.8.8 dettaquat	3.3.3.4.3.4 statset
(4 4 4)	4.4.4.4.4.4.4.4 osquat	4.4.4.4.4.4.4.4 osquat	4.4.4.4.4.4 osquat	4.8.4.8 teokt	4.8.4.8 teokt	4.8.4.8 teokt	8.8.8 okat	3.4.3.4.3.4 dittitecat

•      Coxeter, Harold Scott MacDonald ; Longuet-Higgins, MS; Miller, JCP (1954). "Uniform polyedra". Philosophical Transactions of the Royal Society of London. Serie A. Matematiska och fysiska vetenskaper . Royal Society. 246 (916): 401–450. doi : 10.1098/rsta.1954.0003 . ISSN 0080-4614 . JSTOR 91532 . MR 0062446 . S2CID 202575183 . [1]
•    Skilling, J. (1974). "Den kompletta uppsättningen av enhetliga polyedrar". Philosophical Transactions of the Royal Society of London. Serie A. Matematiska och fysiska vetenskaper . Royal Society. 278 (1278): 111–135. doi : 10.1098/rsta.1975.0022 . ISSN 1364-503X . S2CID 122634260 . [2]

Richard Klitzing: Polyhedra av

• punkt-grupp symmetri
• komplexitet
• Schwarz trianglar del 1 , del 2
• Euklidiska tesselleringar och honungskakor
• Hyperboliska tesseller och bikakor

Tabellerna är baserade på de som presenteras av Klitzing på hans sida.

externa länkar

Jim McNeill:

• Tesselleringar av planet

Zvi Har'El:

• Uniform lösning för Uniform Polyhedra

Hironori Sakamoto:

• Uniform Tessellations på Euklidplanet