Snub (geometri)

De två snubbade arkimedeiska fasta ämnen
Snub kub eller Snub cuboctahedron	Snub dodecahedron eller Snub icosidodecahedron

Två kirala kopior av snubbkuben, som alternerade (röda eller gröna) hörn av den trunkerade kuboktaedern.

En snubbkub kan konstrueras från en rombikuboktaeder genom att rotera de 6 blå fyrkantiga ytorna tills de 12 vita fyrkantiga ytorna blir par av liksidiga triangelytor.

Inom geometri är en snub en operation som appliceras på en polyeder . Termen härstammar från Keplers namn på två arkimediska fasta ämnen , för kuben ( cubus simus ) och snubben dodekaeder ( dodecaedron simum) . I allmänhet har snubbar kiral symmetri med två former: medurs eller moturs orientering. Med Keplers namn kan en snubb ses som en expansion av en vanlig polyeder : flytta ansikten isär, vrida dem runt deras centra, lägga till nya polygoner centrerade på de ursprungliga hörnen och lägga till par av trianglar som passar mellan de ursprungliga kanterna.

Terminologin generaliserades av Coxeter , med en något annorlunda definition, för en bredare uppsättning enhetliga polytoper .

Conway snubbar

John Conway utforskade generaliserade polyederoperatorer, och definierade vad som nu kallas Conway polyhedron notation , som kan appliceras på polyedrar och plattsättningar. Conway kallar Coxeters operation för en semi-snub .

I denna notation definieras snub av dubbel- och gyrooperatorerna , som s = dg , och det är ekvivalent med en alternering av en trunkering av en ambo- operator. Conways notation i sig undviker Coxeters alternerande (halva) operation eftersom den bara gäller för polyedrar med endast jämna ytor.

Snubbade vanliga figurer
Formar att snubba	Polyhedra			Euklidiska plattsättningar		Hyperboliska plattor
Namn	Tetraeder	Kub eller oktaeder	Ikosaeder eller dodekaeder	Fyrkantig plattsättning	Sexkantigt kakel eller Triangulärt kakel	Heptagonal plattsättning eller Order-7 triangulär plattsättning
Bilder
Snubbad form Conway- notation	sT	sC = sO	sI = sD	sQ	sH = sΔ	sΔ ₇
Bild

I 4-dimensioner, föreslår Conway att snub 24-cellen bör kallas en semi-snub 24-cell eftersom, till skillnad från 3-dimensionella snub polyedrar är alternerade omnitruncerade former, det är inte en alternerad omnitruncerad 24-cell . Det är istället faktiskt en alternerad trunkerad 24-cell .

Coxeters snubbar, regelbundna och kvasiregelbundna

Snub kub, härledd från kub eller cuboctahedron
namn	Kub	Cuboctahedron Rättad kub	Stympad cuboctahedron Kantitrunkerad kub	Snub cuboctahedron Snub rätad kub
	Utsäde	Rättad r	Trunkerad t	Omväxlande h
Conway notation	C	CO rC	tCO trC eller trO	htCO = sCO htrC = srC
Schläfli symbol	{4,3}	${\begin{Bmatrix}4\\3\end{Bmatrix}}$ eller r{4,3}	$t{\begin{Bmatrix}4\\3\end{Bmatrix}}$ eller tr{4,3}	$ht{\begin{Bmatrix}4\\3\end{Bmatrix}}=s{\begin{Bmatrix}4\\3\end{Bmatrix}}$ htr{4,3} = sr{4,3}
Coxeter diagram		eller	eller	eller
Bild

Coxeters snubterminologi är något annorlunda, vilket betyder en omväxlande trunkering , som härleder snubkuben som en snub cuboctahedron och snub dodecahedron som en snub icosidodecahedron . Den här definitionen används i namngivningen av två Johnson-fasta ämnen : den snubbade disfenoiden och den snubbade kvadratiska antiprisman , och av högre dimensionella polytoper, såsom den 4-dimensionella snubben 24-cellen , med utökad Schläfli-symbol s{3,4,3} och Coxeter-diagram .

En vanlig polyeder (eller plattsättning), med Schläfli-symbolen ${\begin{Bmatrix}p,q\end{Bmatrix}}$ och Coxeter-diagram , har trunkering definierad som ${\displaystyle t{\begin{Bmatrix}p,q\end{Bmatrix}}} ,$ och , och har snub definierad som en alternerad trunkering $ht{ \begin{Bmatrix}p,q\end{Bmatrix}}=s{\begin{Bmatrix}p,q\end{Bmatrix}}$ och . Denna alternerade konstruktion kräver q är jämnt.

En kvasiregulär polyeder , med Schläfli-symbolen ${\begin{Bmatrix}p\\q\end{Bmatrix}}$ eller r { p , q }, och Coxeter-diagram eller , har kvasiregulär trunkering definierad som $t{\begin{Bmatrix}p\\q\end{Bmatrix}}$ eller tr { p , q } och eller , och har kvasiregular snub definierad som en alternerad trunkerad likriktning $ht{\begin{Bmatrix}p\\q\end{Bmatrix}}=s{\begin{Bmatrix}p\\q\end{Bmatrix}}$ eller htr { p , q } = sr { p , q } och eller .

kommer Keplers snubkub från den kvasiregelbundna kuboktaedern , med en vertikal Schläfli-symbol ${\begin{Bmatrix}4\\3\end{Bmatrix}}$ och Coxeter-diagrammet , och så är mer uttryckligen kallad en snub cuboctahedron , uttryckt av en vertikal Schläfli-symbol $s{\begin{Bmatrix}4\\3\end{Bmatrix}}$ och Coxeter-diagram . Den snubbade kuboktaedern är växlingen av den trunkerade kuboktaedern , ${\displaystyle t{\begin{Bmatrix}4\\3\end{Bmatrix}}} ,$ och .

Reguljära polyedrar med jämn ordningshörn kan också snubbas som alternerade trunkationer, som den snubbade oktaedern , eftersom ${\displaystyle s{\begin{Bmatrix}3,4\end{Bmatrix}}} ,$ , är växlingen av den trunkerade oktaedern , ${\displaystyle t{\begin{Bmatrix}3,4\end{Bmatrix}}} ,$ och . Den snubbade oktaedern representerar pseudoikosaedern , en vanlig ikosaeder med pyritoedrisk symmetri .

Den snubbade tetratetraedern , som ${\displaystyle s{\begin{Bmatrix}3\\3\end{Bmatrix}}} ,$ och , är växlingen av den trunkerade tetraedriska symmetriformen, $t{\begin{Bmatrix}3\\3\end{Bmatrix}}$ och .

namn	Oktaeder	Stympad oktaeder	Snub oktaeder
	Utsäde	Trunkerad t	Omväxlande h
Conway notation	O	till	htO eller sO
Schläfli symbol	{3,4}	t{3,4}	ht{3,4} = s{3,4}
Coxeter diagram
Bild

Coxeters snubboperation tillåter också att n- antiprismor definieras som $s{\begin{Bmatrix}2\\n\end{Bmatrix}}$ eller $s {\begin{Bmatrix}2,2n\end{Bmatrix}}$ , baserat på n-prismor $t{\begin{Bmatrix}2\\n\end{Bmatrix}}$ eller ${\displaystyle t{\begin{Bmatrix}2,2n\end{Bmatrix}}} ,$ medan ${\begin{Bmatrix}2,n\end{Bmatrix} }$ är en vanlig n- hosohedron , en degenererad polyeder, men en giltig plattsättning på sfären med digon- eller luneformade ytor.

Snub hosohedra , {2,2p}
Bild
Coxeter diagram							... ...
Schläfli symboler	s{2,4}	s{2,6}	s{2,8}	s{2,10}	s{2,12}	s{2,14}	s{2,16} ...	s{2,∞}
Schläfli symboler	sr{2,2} $s{\begin{Bmatrix}2\\2\end{Bmatrix}}$	sr{2,3} $s{\begin{Bmatrix}2\\3\end{Bmatrix}}$	sr{2,4} $s{\begin{Bmatrix}2\\4\end{Bmatrix}}$	sr{2,5} $s{\begin{Bmatrix}2\\5\end{Bmatrix}}$	sr{2,6} $s{\begin{Bmatrix}2\\6\end{Bmatrix}}$	sr{2,7} $s{\begin{Bmatrix}2\\7\end{Bmatrix}}$	sr{2,8}... $s{\begin{Bmatrix}2\\8\end{Bmatrix}}$ ...	sr{2,∞} $s{\begin{Bmatrix}2\\\infty \end{Bmatrix}}$
Conway notation	A2 = T	A3 = O	A4	A5	A6	A7	A8...	A∞

Samma process gäller för kakelplattor:

Triangulär plattsättning Δ	Trunkerad triangulär plattsättning tΔ	Snub triangulär plattsättning htΔ = sΔ
{3,6}	t{3,6}	ht{3,6} = s{3,6}

Exempel

Snubs baserat på {s,4}
Plats	Sfärisk		euklidisk	Hyperbolisk
Bild
Coxeter diagram								...
Schläfli symbol	s{2,4}	s{3,4}	s{4,4}	s{5,4}	s{6,4}	s{7,4}	s{8,4}	... s{∞,4}

Kvasiregelbundna snubbar baserade på r{p,3}
Conway notation	Sfärisk				euklidisk	Hyperbolisk
Bild
Coxeter diagram								...
Schläfli symbol	sr{2,3}	sr{3,3}	sr{4,3}	sr{5,3}	sr{6,3}	sr{7,3}	sr{8,3}	... sr{∞,3}
Schläfli symbol	$s{\begin{Bmatrix}2\\3\end{Bmatrix}}$	$s{\begin{Bmatrix}3\\3\end{Bmatrix}}$	$s{\begin{Bmatrix}4\\3\end{Bmatrix}}$	$s{\begin{Bmatrix}5\\3\end{Bmatrix}}$	$s{\begin{Bmatrix}6\\3\end{Bmatrix}}$	$s{\begin{Bmatrix}7\\3\end{Bmatrix}}$	$s{\begin{Bmatrix}8\\3\end{Bmatrix}}$	$s{\begin{Bmatrix}\infty \\3\end{Bmatrix}}$
Conway notation	A3	sT	sC eller sO	sD eller SI	sΗ eller sΔ

Kvasiregelbundna snubbar baserade på r{p,4}
Plats	Sfärisk		euklidisk	Hyperbolisk
Bild
Coxeter diagram								...
Schläfli symbol	sr{2,4}	sr{3,4}	sr{4,4}	sr{5,4}	sr{6,4}	sr{7,4}	sr{8,4}	... sr{∞,4}
Schläfli symbol	$s{\begin{Bmatrix}2\\4\end{Bmatrix}}$	$s{\begin{Bmatrix}3\\4\end{Bmatrix}}$	$s{\begin{Bmatrix}4\\4\end{Bmatrix}}$	$s{\begin{Bmatrix}5\\4\end{Bmatrix}}$	$s{\begin{Bmatrix}6\\4\end{Bmatrix}}$	$s{\begin{Bmatrix}7\\4\end{Bmatrix}}$	$s{\begin{Bmatrix}8\\4\end{Bmatrix}}$	$s{\begin{Bmatrix}\infty \\4\end{Bmatrix}}$
Conway notation	A4	sC eller sO	sQ

Olikformiga snubbiga polyedrar

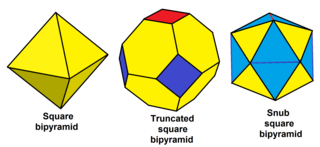
Olikformiga polyedrar med alla jämn valans hörn kan avstängas, inklusive några oändliga uppsättningar; till exempel:

Snub bipyramids sdt{2,p}
Snub fyrkantig bipyramid


Snub hexagonal bipyramid

Snub rätade bipyramider srdt{2,p}

Snub antiprismor s{2,2p}
Bild				...
Schläfli symboler	ss{2,4}	ss{2,6}	ss{2,8}	ss{2,10}...
Schläfli symboler	ssr{2,2} $ss{\begin{Bmatrix}2\\2\end{Bmatrix}}$	ssr{2,3} $ss{\begin{Bmatrix}2\\3\end{Bmatrix}}$	ssr{2,4} $ss{\begin{Bmatrix}2\\4\end{Bmatrix}}$	ssr{2,5}... $ss{\begin{Bmatrix}2\\5\end{Bmatrix}}$

Coxeters enhetliga stjärn-polyhedra

Snub star-polyhedra är konstruerade av deras Schwarz triangel (pqr), med rationellt ordnade spegelvinklar, och alla speglar aktiva och alternerade.

Snubbade enhetliga stjärnpolyeder
s{3/2,3/2}	s{(3,3,5/2)}	sr{5,5/2}	s{(3,5,5/3)}	sr{5/2,3}
sr{5/3,5}	s{(5/2,5/3,3)}	sr{5/3,3}	s{(3/2,3/2,5/2)}	s{3/2,5/3}

Coxeters högredimensionella avstängda polytoper och honungskakor

I allmänhet har en vanlig polykoron med Schläfli-symbol ${\displaystyle {\begin{Bmatrix}p,q,r\end{Bmatrix}}} ,$ och Coxeter-diagram , en snubb med utökad Schläfli-symbol $s{\begin{Bmatrix}p,q,r\end{Bmatrix}}$ och .

En likriktad polykoron ${\begin{Bmatrix}p\\q,r\end{Bmatrix}}$ = r{p,q,r} och har snubbsymbol $s{\begin{Bmatrix}p\\q,r\end{Bmatrix}}$ = sr{p,q,r} och .

Exempel

Ortogonal projektion av snub 24-cell

Det finns bara en enhetlig konvex snubb i 4-dimensioner, snubben 24-cell . Den vanliga 24-cellen har Schläfli-symbolen , ${\begin{Bmatrix}3,4,3\end{Bmatrix}}$ och Coxeter-diagram , och 24-cellens snäva representeras av $s{\begin{Bmatrix}3,4,3\end{Bmatrix}}$ , Coxeter-diagram . Den har också ett index med 6 lägre symmetrikonstruktioner som $s\left\{{\begin{array}{l}3\\3\\3\end{array}}\right\}$ eller s{3 ^1,1,1 } och , och en index 3 subsymmetri som $s{\begin{Bmatrix}3\\3,4\end{Bmatrix}}$ eller sr{3,3,4} och eller .

Den relaterade snubben 24-cells honeycomb kan ses som en $s{\begin{Bmatrix}3,4,3,3\end{Bmatrix}}$ eller s{3 ,4,3,3} och , och lägre symmetri $s{\begin{Bmatrix}3\\3,4,3\end{Bmatrix}}$ eller sr{ 3,3,4,3} och eller , och lägsta symmetriform som $s\left\{{\begin{array}{l}3\\3\\3\\3 \end{array}}\right\}$ eller s{3 ^1,1,1,1 } och .

En euklidisk honeycomb är en alternerad hexagonal platta honeycomb , s{2,6,3} och eller sr{2,3,6} och eller sr{2,3 ^[3] }, och .

En annan euklidisk (skaliform) bikaka är en bikaka med omväxlande kvadratisk skiva , s{2,4,4} och eller sr{2,4 ^1,1 } och :

Den enda likformiga, likformiga, hyperboliska likformiga bikakan är den hexagonala bikakan med hexagonal kakel , som s{3,6,3} och , som också kan konstrueras som en alternerad hexagonal kakelbikaka , h{6,3,3}, . Den är också konstruerad som s{3 ^[3,3] } och .

En annan hyperbolisk (skaliform) bikaka är en oktaedrisk bikakekaka av 4-gradig ordning, s{3,4,4} och .

Se även

Snub polyeder

Polyederoperatörer
Utsäde	Avkortning	Rättelse	Bitrunkation	Dubbel	Expansion	Omnitruncation	Växlingar


$0 t {p, q} {p, q}$	$t 01 {p, q} t {p, q}$	$t 1 {p, q} r {p, q}$	$t 12 {p, q} 2t {p, q}$	$t 2 {p, q} 2r {p, q}$	$t 02 {p, q} rr {p, q}$	$t 012 {p, q} tr {p, q}$	$0 ht {p, q} h {q, p}$	$ht 12 {p, q} s {q, p}$	$ht 012 {p, q} sr {p, q}$

Coxeter, Harold Scott MacDonald ; Longuet-Higgins, MS; Miller, JCP (1954). "Uniform polyedra". Philosophical Transactions of the Royal Society of London. Serie A. Matematiska och fysiska vetenskaper . Royal Society. 246 (916): 401–450. Bibcode : 1954RSPTA.246..401C . doi : 10.1098/rsta.1954.0003 . ISSN 0080-4614 . JSTOR 91532 . MR 0062446 . S2CID 202575183 .
Coxeter, HSM Regular Polytopes , (3:e upplagan, 1973), Dover-upplagan, ISBN 0-486-61480-8 (s. 154–156 8.6 Partiell trunkering, eller alternering)
Kaleidoscopes: Selected Writings of HSM Coxeter , redigerad av F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1] , Googlebooks [ 2]
- (Paper 17) Coxeter , The Evolution of Coxeter–Dynkin diagrams , [Nieuw Archief voor Wiskunde 9 (1991) 233–248]
- (Papper 22) HSM Coxeter, Regular and Semi Regular Polytopes I , [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- (Papper 23) HSM Coxeter, Regular and Semi-Regular Polytopes II , [Math. Zeit. 188 (1985) 559–591]
- (Papper 24) HSM Coxeter, Regular and Semi-Regular Polytopes III , [Math. Zeit. 200 (1988) 3–45]
Coxeter , The Beauty of Geometry: Twelve Essays , Dover Publications, 1999, ISBN 978-0-486-40919-1 (Kapitel 3: Wythoff's Construction for Uniform Polytopes)
Norman Johnson Uniform Polytopes , Manuscript (1991)
- NW Johnson : Theory of Uniform Polytopes and Honeycombs , Ph.D. Avhandling, University of Toronto, 1966
John H. Conway , Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5
Weisstein, Eric W. "Snubification" . MathWorld .
Richard Klitzing, Snubs, alternated facetings, and Stott-Coxeter-Dynkin diagrams , Symmetry: Culture and Science, Vol. 21, No.4, 329–344, (2010) [3]