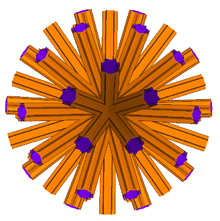
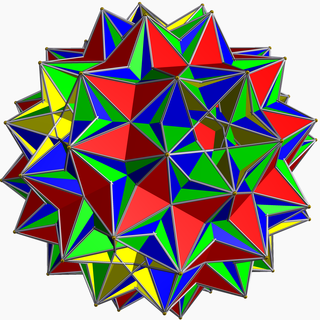
Stor disnub dirhombidodecahedron

Stor disnub dirhombidodecahedron

Typ	Uniform stjärnpolyeder
Element	F = 204, E = 360 V = 60 (χ = -96)
Ansikten vid sida	120{3}+60{4}+24{5/2}
Coxeter diagram	{{{Skilling-Coxeter}}}
Wythoff symbol	\| (3/2) 5/3 (3) 5/2
Symmetrigrupp	I _h , [5,3], *532
Indexreferenser	U _- , C _- , W _-
Dubbel polyeder	Bra disnub dirhombidodecacron
Vertex figur	(5/2.4.3.3.3.4. 5/3.4.3/2.3/2.3/2.4)/ ₂
Bowers förkortning	Gidisdrid

3D-modell av en stor disnub dirhombidodecahedron

Inom geometri är den stora disnub dirhombidodecahedronen , även kallad Skillings figur , en degenererad enhetlig stjärnpolyeder .

Det bevisades 1970 att det bara finns 75 enhetliga polyedrar förutom de oändliga familjerna av prismor och antiprismor . John Skilling upptäckte ett annat degenererat exempel, den stora disnub dirhombidodecahedron, genom att slappna av villkoret att kanterna måste vara enkla. Närmare bestämt tillät han en jämn mängd ansikten att mötas vid varje kant, så länge som uppsättningen ansikten inte kunde separeras i två sammankopplade uppsättningar (Skilling, 1975). På grund av att dess geometriska realisering har några dubbla kanter där 4 ytor möts, anses den vara en degenererad enhetlig polyeder men inte strikt en enhetlig polyeder.

Antalet kanter är tvetydigt, eftersom den underliggande abstrakta polyedern har 360 kanter, men 120 par av dessa har samma bild i den geometriska realiseringen, så att den geometriska realiseringen har 120 enkelkanter och 120 dubbelkanter där 4 ytor möts, för en totalt 240 kanter. Eulerkarakteristiken för den abstrakta polyedern är -96. Om paren av sammanfallande kanter i den geometriska realiseringen anses vara enkelkanter, så har den bara 240 kanter och Euler-karaktäristik 24.

Topfiguren har 4 fyrkantiga ytor som går genom modellens mitt .

Den kan konstrueras som den exklusiva eller (blandning) av den stora dirhombicosidodecahedronen och sammansättningen av tjugo oktaedrar .

Besläktade polyedrar

Den delar samma kantarrangemang som den stora dirhombicosidodecahedronen , men har en annan uppsättning triangulära ytor. Topparna och kanterna delas också med de enhetliga föreningarna av tjugo oktaedrar eller tjugo tetrahemihexaedrar . 180 av kanterna delas med den stora snubben dodecicosidodecahedron .

Konvext skrov	Stor snubbig dodecicosidodecahedron	Stor dirhombicosidodecahedron
Stor disnub dirhombidodecahedron	Sammansättning av tjugo oktaedrar	Förening av tjugo tetrahemihexaedrar

Dubbel polyeder

Den stora disnub dirhombidodecacron

Dualen av den stora disnub dirhombidodecahedronen kallas den stora disnub dirhombidodecacron . Det är en icke-konvex oändlig isoedrisk polyeder .

Liksom det visuellt identiska stora dirhombicosidodecacronet i Magnus Wenningers Dual Models , är det representerat med korsande oändliga prismor som passerar genom modellens centrum, avskurna vid en viss punkt som är bekväm för tillverkaren. Wenninger föreslog att dessa figurer är medlemmar i en ny klass av stellation polyedra, kallad stellation to infinity . Men han erkände också att de strängt taget inte är polyedrar eftersom deras konstruktion inte överensstämmer med de vanliga definitionerna.

Galleri

Traditionell fyllning	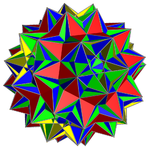Modulo-2 fyllning

Se även

Lista över enhetliga polyedrar

Skilling, John (1975), "The complete set of uniform polyhedra", Philosophical Transactions of the Royal Society A , 278 (1278): 111–135, doi : 10.1098/rsta.1975.0022 .
Weisstein, Eric W. "Stora dirhombicosidodecahedron" . MathWorld .
http://www.software3d.com/MillersMonster.php

externa länkar