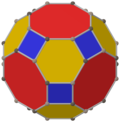
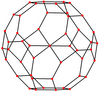
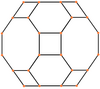
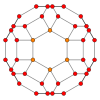
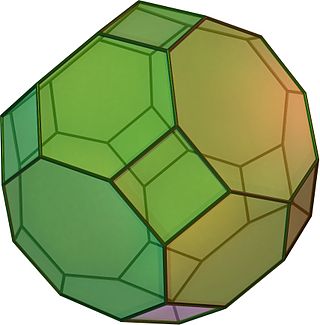
Stympad cuboctahedron
| Trunkerad cuboctahedron | |
|---|---|
 (Klicka här för roterande modell) |
|
| Typ |
Arkimedesk solid Uniform polyeder |
| Element | F = 26, E = 72, V = 48 (χ = 2) |
| Ansikten vid sida | 12{4}+8{6}+6{8} |
| Conway notation | bC eller taC |
| Schläfli symboler | tr{4,3} eller |
| t 0,1,2 {4,3} | |
| Wythoff symbol | 2 3 4 | |
| Coxeter diagram |
|
| Symmetrigrupp | O h , B 3 , [4,3], (*432), ordning 48 |
| Rotationsgrupp | O , [4,3] + , (432), ordning 24 |
| Dihedral vinkel |
4-6: arccos(− √6 / 3 ) = 144°44′08″ 4-8: arccos(− 1 / √2 ) = 135° 6-8: arccos(− √3 / 3 ) = 125°15 "51" |
| Referenser | U11 , C23 , W15 _ _ _ |
| Egenskaper | Halvregelbunden konvex zonohedron |
 Färgade ansikten |
 4.6.8 ( Vertex figur ) |
 Disdyakis dodecahedron ( dubbel polyeder ) |
 Netto |
Inom geometrin är den trunkerade kuboktaedern en arkimedisk fast substans , namngiven av Kepler som en trunkering av en kuboktaeder . Den har 12 fyrkantiga ytor, 8 regelbundna sexkantiga ytor, 6 regelbundna åttakantiga ytor, 48 hörn och 72 kanter. Sedan var och en av dess vänder mot har peka symmetri (motsvarande 180° rotationssymmetri ), är den trunkerade kuboktaedern en 9 - zonohedron . Den stympade kuboktaedern kan tessellates med det åttakantiga prismat .
Namn
|
Namnet trunkerad cuboctahedron , som ursprungligen gavs av Johannes Kepler , är missvisande: en faktisk trunkering av en cuboctahedron har rektanglar istället för kvadrater ; emellertid är denna olikformiga polyeder topologiskt ekvivalent med den arkimediska fasta kroppskroppen som oriktigt benämnts trunkerade cuboctahedron. Alternativa utbytbara namn är:
|
Det finns en icke-konvex enhetlig polyeder med ett liknande namn: den icke-konvexa stora rhombicuboctahedronen .
kartesiska koordinater
De kartesiska koordinaterna för hörn av en stympad kuboktaeder med kantlängd 2 och centrerad vid origo är alla permutationer av :
- (±1, ±(1 + √ 2 ), ± (1 + 2 √ 2 )).
Yta och volym
Arean A och volymen V för den trunkerade kuboktaedern med kantlängd a är:
Dissektion
Den trunkerade kuboktaedern är det konvexa skrovet av en rhombicuboctahedron med kuber ovanför dess 12 rutor på 2-faldiga symmetriaxlar. Resten av dess utrymme kan dissekeras i 6 kvadratiska kupoler under oktagonerna och 8 triangulära kupoler under sexkanterna.
En dissekerad stympad kuboktaeder kan skapa ett släkte 5, 7 eller 11 Stewart toroid genom att ta bort den centrala rhombicuboctahedron, och antingen de 6 kvadratiska kupolerna, de 8 triangulära kupolerna respektive de 12 kuberna. Många andra toroider med lägre symmetri kan också konstrueras genom att ta bort den centrala rhombicuboctahedronen och en delmängd av de andra dissektionskomponenterna. Till exempel, att ta bort 4 av de triangulära kupolerna skapar en släkte 3 toroid; om dessa kupoler väljs på lämpligt sätt, har denna toroid tetraedrisk symmetri.
| Stewart toroider | |||
|---|---|---|---|
| Genus 3 | Genus 5 | Genus 7 | Genus 11 |

|

|

|

|
Enhetliga färger
Det finns bara en enhetlig färgning av ansiktena på denna polyeder, en färg för varje ansiktstyp.
En 2-likformig färgning, med tetraedrisk symmetri , finns med växelvis färgade hexagoner.
Ortogonala projektioner
Den trunkerade kuboktaedern har två speciella ortogonala projektioner i A 2 och B 2 Coxeter-planen med [6] och [8] projektiv symmetri, och många [2] symmetrier kan konstrueras från olika projicerade plan i förhållande till polyederelementen.
Sfärisk plattsättning
Den stympade kuboktaedern kan också representeras som en sfärisk plattsättning och projiceras på planet via en stereografisk projektion . Denna projektion är konform och bevarar vinklar men inte ytor eller längder. Raka linjer på sfären projiceras som cirkelbågar på planet.

|

|

|

|
| Ortogonal projektion | kvadratiskt centrerad | hexagon -centrerad | oktagoncentrerad _ |
|---|---|---|---|
| Stereografiska projektioner | |||
Hel oktaedrisk grupp
Liksom många andra fasta ämnen har den trunkerade oktaedern full oktaedrisk symmetri - men dess förhållande till den fullständiga oktaedriska gruppen är närmare än så: Dess 48 hörn motsvarar elementen i gruppen, och varje sida av dess dual är en grundläggande domän för gruppen.
Bilden till höger visar de 48 permutationerna i gruppen som tillämpas på ett exempelobjekt (nämligen den lätta JF-föreningen till vänster). De 24 ljusa elementen är rotationer och de mörka är deras reflektioner.
Kanterna på det fasta materialet motsvarar de 9 reflektionerna i gruppen:
- De mellan oktagoner och kvadrater motsvarar de 3 reflektionerna mellan motsatta oktagoner.
- Hexagonkanter motsvarar de 6 reflektionerna mellan motsatta kvadrater.
- (Det finns inga reflektioner mellan motsatta hexagoner.)
Undergrupperna motsvarar fasta ämnen som delar respektive hörn av den trunkerade oktaedern. T.ex. motsvarar de 3 undergrupperna med 24 element en olikformig kub med kiral oktaedrisk symmetri, en olikformig rhombicuboctahedron med pyritohedrisk symmetri (den cantic snub oktaedern ) och en olikformig trunkerad oktaeder med full tetraedrisk symmetri . Den unika undergruppen med 12 element är den alternerande gruppen A 4 . Det motsvarar en olikformig ikosaeder med kiral tetraedrisk symmetri .
| Undergrupper och motsvarande fasta ämnen | ||||
|---|---|---|---|---|
|
Stympad cuboctahedron tr{4,3} |
Snub kub sr{4,3} |
Rhombicuboctahedron s 2 {3,4} |
Trunkerad oktaeder h 1,2 {4,3} |
Icosahedron |
|
[4,3] Hel oktaedrisk |
[4,3] + Kiral oktaedral |
[4,3 + ] Pyritohedral |
[1 + ,4,3] = [3,3] Full tetraedrisk |
[1 + ,4,3 + ] = [3,3] + Kiral tetraedrisk |

|

|

|

|

|
| alla 48 hörn | 24 hörn | 12 hörn | ||
Besläktade polyedrar

|

|
| Bowtie tetraeder och kub innehåller två trapetsformade ytor i stället för varje kvadrat. | |
Den trunkerade kuboktaedern är en av en familj av enhetliga polyedrar som är relaterade till kuben och den vanliga oktaedern.
| Uniforma oktaedriska polyedrar | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Symmetri : [4,3], (*432) |
[4,3] + (432) |
[1 + ,4,3] = [3,3] (*332) |
[3 + ,4] (3*2) |
|||||||
| {4,3} | t{4,3} |
r{4,3} r{3 1,1 } |
t{3,4} t{3 1,1 } |
{3,4} {3 1,1 } |
rr{4,3} s 2 {3,4} |
tr{4,3} | sr{4,3} |
h{4,3} {3,3} |
h 2 {4,3} t{3,3} |
s{3,4} s{3 1,1 } |
|
|
|
|
|
|
|
|
|
|
||
|
= |
= |
= |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
| Dual till enhetliga polyedrar | ||||||||||
| V4 3 | V3.8 2 | V(3.4) 2 | V4.6 2 | V3 4 | V3.4 3 | V4.6.8 | V3 4 .4 | V3 3 | V3.6 2 | V3 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
![]()
![]()
![]()
![]()
![]() Denna polyeder kan betraktas som en medlem av en sekvens av enhetliga mönster med vertexkonfiguration (4.6.2 p ) och Coxeter-Dynkin-diagram . För p < 6 är medlemmarna i sekvensen omnitrunkerade polyedrar ( zonohedron ), som visas nedan som sfäriska plattsättningar. För p < 6 är de plattsättningar av det hyperboliska planet, som börjar med den trunkerade triheptagonala plattsättningen .
Denna polyeder kan betraktas som en medlem av en sekvens av enhetliga mönster med vertexkonfiguration (4.6.2 p ) och Coxeter-Dynkin-diagram . För p < 6 är medlemmarna i sekvensen omnitrunkerade polyedrar ( zonohedron ), som visas nedan som sfäriska plattsättningar. För p < 6 är de plattsättningar av det hyperboliska planet, som börjar med den trunkerade triheptagonala plattsättningen .
| * n 32 symmetrimutation av omnitrunkerade plattsättningar: 4.6.2n | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Sym. * n 32 [ n ,3] |
Sfärisk | Euklid. | Kompakt hyperb. | Paraco. | Icke-kompakt hyperbolisk | |||||||
|
*232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3] |
*∞32 [∞,3] |
[12i,3] |
[9i,3] |
[6i,3] |
[3i,3] |
|
| Siffror |
|

|

|

|

|

|

|

|

|

|

|

|
| Konfig. | 4.6.4 | 4.6.6 | 4.6.8 | 4.6.10 | 4.6.12 | 4.6.14 | 4.6.16 | 4.6.∞ | 4.6.24i | 4.6.18i | 4.6.12i | 4.6.6i |
| Dualer |

|

|

|

|

|

|

|

|

|

|

|

|
| Konfig. | V4.6.4 | V4.6.6 | V4.6.8 | V4.6.10 | V4.6.12 | V4.6.14 | V4.6.16 | V4.6.∞ | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
| * n 42 symmetrimutation av omnitrunkerade plattsättningar: 4.8.2n | ||||||||
|---|---|---|---|---|---|---|---|---|
|
Symmetri * n 42 [n,4] |
Sfärisk | euklidisk | Kompakt hyperbolisk | Paracomp. | ||||
|
*242 [2,4] |
*342 [3,4] |
*442 [4,4] |
*542 [5,4] |
*642 [6,4] |
*742 [7,4] |
*842 [8,4]... |
*∞42 [∞,4] |
|
|
Omnitruncerad figur |
 4.8.4 |
 4.8.6 |
 4.8.8 |
 4.8.10 |
 4.8.12 |
 4.8.14 |
 4.8.16 |
 4.8.∞ |
|
Omnitruncerade dualer |
 V4.8.4 |
 V4.8.6 |
 V4.8.8 |
 V4.8.10 |
 V4.8.12 |
 V4.8.14 |
 V4.8.16 |
 V4.8.∞ |
| * n 32 symmetrimutation av omnitrunkerade plattsättningar: 6.8.2n | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Sym. * n 43 [( n ,4,3)] |
Sfärisk | Kompakt hyperbolisk | Paraco. | |||||||||
|
*243 [4,3] |
*343 [(3,4,3)] |
*443 [(4,4,3)] |
*543 [(5,4,3)] |
*643 [(6,4,3)] |
*743 [(7,4,3)] |
*843 [(8,4,3)] |
*∞43 [(∞,4,3)] |
|||||
| Siffror |

|

|

|

|

|

|

|

|
||||
| Konfig. | 4.8.6 | 6.8.6 | 8.8.6 | 10.8.6 | 12.8.6 | 14.8.6 | 16.8.6 | ∞.8.6 | ||||
| Dualer |

|

|

|

|

|

|

|

|
||||
| Konfig. | V4.8.6 | V6.8.6 | V8.8.6 | V10.8.6 | V12.8.6 | V14.8.6 | V16.8.6 | V6.8.∞ | ||||
Det är först i en serie av cantitruncerade hyperkuber:
 
|
 
|
 
|
 
|
 
|
 
|
| Stympad cuboctahedron | Cantitruncated tesseract | Cantitruncerad 5-kub | Cantitruncerad 6-kub | Cantitruncerad 7-kub | Cantitruncerad 8-kub |
|
|
|
|
|
|
|
Trunkerad cuboctaedral graf
| Trunkerad cuboctaedral graf | |
|---|---|
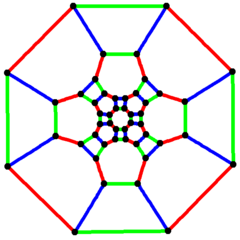 4-faldig symmetri
| |
| Vertices | 48 |
| Kanter | 72 |
| Automorfismer | 48 |
| Kromatiskt nummer | 2 |
| Egenskaper | Kubisk , Hamiltonsk , regelbunden , nollsymmetrisk |
| Tabell över grafer och parametrar | |
Inom det matematiska fältet av grafteorin är en trunkerad kuboktaedrisk graf (eller stor rhombcuboctahedral graf ) grafen över hörn och kanter av den trunkerade kuboktaedern, en av arkimedeiska fasta ämnen . Den har 48 hörn och 72 kanter och är en nollsymmetrisk och kubisk arkimedeansk graf .
Se även
- Kub
- Cuboctahedron
- Oktaeder
- Stympad icosidodecahedron
- Trunkerad oktaeder – trunkerad tetratetraeder
- Snub kub
- Cromwell, P. (1997). Polyeder . Storbritannien: Cambridge. s. 79–86 Arkimedeiska fasta ämnen . ISBN 0-521-55432-2 .
externa länkar
- Eric W. Weisstein , Great rhombicuboctahedron ( Arkimedean solid) på MathWorld .
- Klitzing, Richard. "3D konvexa likformiga polyedrar x3x4x - girco" .
- Redigerbart utskrivbart nät av en trunkerad kuboktaeder med interaktiv 3D-vy
- Den enhetliga polyedern
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- Stor rhombicuboctahedron: pappersremsor för flätning