Kvasiregelbunden polyeder

Kvasiregelbundna figurer Rätt triangeldomäner (pq 2), = r{p,q} r{4,3} r{5,3} r{6,3} r{7,3} ... r{∞,3} (3.4) 2 (3.5) 2 (3.6) 2 (3.7) 2 (3.∞) 2 Likbenta triangeldomäner (s. 3), = = h{6,p} h{6,4} h{6,5} h{6,6} h{6,7}... h{6,∞} = = = = = (4.3) 4 (5.3) 5 (6.3) 6 (7.3) 7 (∞.3) ∞ Likbenta triangeldomäner (s. 4), = = h{8,p} h{8,3} h{8,5} h{8,6} h{8,7}... h{8,∞} = = = = = (4.3) 3 (4.5) 5 (4.6) 6 (4.7) 7 (4.∞) ∞ Skalen triangeldomän (5 4 3), (3.5) 4 (4.5) 3 (3.4) 5 En kvasiregelbunden polyeder eller plattsättning har exakt två typer av regelbundna ansikten, som alternerar runt varje vertex. Deras vertexfigurer är isogonala polygoner .

Regelbundna och kvasiregelbundna figurer Rätt triangeldomäner (s. 2), = = r{p,p} = {p,4} 1 ⁄ 2 {3,4} 1 ⁄ 2 r{3,3} {4,4} 1 ⁄ 2 r{4,4} 1⁄2 } { 5,4} r{5,5 1⁄2 ... { 6,4} r{6,6} {∞,4} 1 ⁄ 2 r{∞,∞} = = = = = (3.3) 2 (4.4) 2 (5.5) 2 (6.6) 2 (∞.∞) 2 Likbenta triangeldomäner (s. 3), = = {p,6} 1 ⁄ 2 {3,6} 1 ⁄ 2 } 1⁄2 { 4,6 {5,6} 1 ⁄ 2 1⁄2 ... { 6,6 } {∞,6} 1 ⁄ 2 = = = = = (3.3) 3 (4.4) 3 (5.5) 3 (6.6) 3 (∞.∞) 3 Likbenta triangeldomäner (s. 4), = = {p,8} 1 ⁄ 2 } 1⁄2 { 3,8 } 1⁄2 { 4,8 } 1⁄2 { 5,8 } 1⁄2 { 6,8 ... {∞,8} 1⁄2 = = = = = (3.3) 4 (4.4) 4 (5.5) 4 (6.6) 4 (∞.∞) 4 En vanlig polyeder eller plattsättning kan betraktas som kvasiregelbunden om den har ett jämnt antal ytor runt varje vertex (och därmed kan ha växelvis färgade ytor).

Inom geometrin är en kvasiregelbunden polyeder en enhetlig polyeder som har exakt två sorters regelbundna ytor, som alternerar runt varje vertex . De är vertextransitiva och kanttransitiva , därav ett steg närmare vanliga polyedrar än de semiregular , som bara är vertextransitiva.

Deras dubbla figurer är ansiktstransitiv och kanttransitiv; de har exakt två sorters regelbundna vertexfigurer , som alternerar runt varje ansikte . De anses ibland också vara kvasiregelbundna.

Det finns bara två konvexa kvasiregulära polyedrar: cuboctahedron och icosidodecahedron . Deras namn, givna av Kepler , kommer från att inse att deras ansikten är alla ansikten (vända på olika sätt) av dubbelparkuben och oktaedern , i det första fallet, och av dubbelparets ikosaeder och dodekaeder , i det andra fallet.

Dessa former som representerar ett par av en vanlig figur och dess dual kan ges en vertikal Schläfli-symbol ${\begin{Bmatrix}p\\q\end{Bmatrix}}$ eller r{p,q} , för att representera att deras ansikten är alla ansikten (vända på olika sätt) av både den vanliga {p,q} och den dubbla regelbundna {q,p} . En kvasiregelbunden polyeder med denna symbol kommer att ha en vertexkonfiguration p.qpq (eller (pq) ² ).

Mer allmänt kan en kvasireguljär figur ha en vertexkonfiguration (pq) ^r , som representerar r (2 eller fler) sekvenser av ytorna runt vertexen.

Plattläggning av planet kan också vara kvasiregelbunden, närmare bestämt den trihexagonala plattsättningen , med vertexkonfiguration (3.6) ² . Andra kvasiregelbundna plattor finns på det hyperboliska planet, som den triheptagonala plattsättningen, (3.7) ² . Eller mer allmänt: (pq) ² , med 1/p + 1/q < 1/2 .

Regelbundna polyedrar och plattsättningar med ett jämnt antal ytor vid varje vertex kan också betraktas som kvasiregelbundna genom att skilja mellan ytor av samma ordning, genom att representera dem olika, som att färga dem omväxlande (utan att definiera någon ytorientering). En vanlig figur med Schläfli-symbolen {p,q} kan betraktas som kvasiregelbunden, med vertexkonfiguration (pp) ^q/2 , om q är jämnt.

Exempel:

Den reguljära oktaedern , med Schläfli-symbolen {3,4} och 4 är jämna, kan betraktas som kvasireguljär som en tetrahedron (2 uppsättningar av 4 trianglar av tetraedern ), med vertexkonfiguration (3.3) ^4/2 = (3 _a .3) _b ) ² , omväxlande två färger av triangulära ytor.

Den fyrkantiga plattsättningen , med vertexkonfiguration 4 ⁴ och 4 är jämn, kan betraktas som kvasiregelbunden, med vertexkonfiguration (4.4) ^4/2 = (4 _a .4 _b ) ² , färgad som en schackbräde .

Den triangulära plattsättningen , med vertexkonfiguration 3 ⁶ och 6 är jämn, kan betraktas som kvasiregelbunden, med vertexkonfiguration (3.3) ^6/2 = (3 _a .3 _b ) ³ , alternerande två färger av triangulära ytor.

Wythoff konstruktion

Reguljära ( p | 2 q ) och kvasiregulära polyedrar ( 2 | pq ) skapas från en Wythoff-konstruktion med generatorpunkten i ett av 3 hörn av den fundamentala domänen. Detta definierar en enda kant inom den grundläggande domänen.

Kvasiregelbundna polyedrar genereras från alla 3 hörnen av den fundamentala domänen för Schwarz-trianglar som inte har några räta vinklar: q | 2 p , p | 2 q , 2 | pq

Coxeter definierar en kvasiregelbunden polyeder som en som har en Wythoff-symbol i formen p | qr , och det är regelbundet om q=2 eller q=r.

Coxeter -Dynkin-diagrammet är en annan symbolisk representation som visar den kvasireguljära relationen mellan de två dubbel-reguljära formerna:

Schläfli symbol		Coxeter diagram	Wythoff symbol
${\begin{Bmatrix}p,q\end{Bmatrix}}$	{p,q}		q | 2 sid
${\begin{Bmatrix}q,p\end{Bmatrix}}$	{q,p}		p | 2 q
${\begin{Bmatrix}p\\q\end{Bmatrix}}$	r{p,q}	eller	2 | pq

De konvexa kvasiregelbundna polyedrarna

Ytterligare information: Rättning (geometri)

Det finns två enhetliga konvexa kvasiregelbundna polyedrar:

1. Kuboktaedern ${\begin{Bmatrix}3\\4\end{Bmatrix}}$ , vertexkonfiguration (3.4) ² , Coxeter-Dynkin - diagram
2. Icosidodecahedron ${\begin{Bmatrix}3\\5\end{Bmatrix}}$ , vertexkonfiguration (3.5) ² , Coxeter-Dynkin-diagram

Dessutom kan oktaedern , som också är regelbunden , ${\displaystyle {\begin{Bmatrix}3\\3\end{Bmatrix}}} ,$ vertexkonfiguration (3.3) ² , betraktas som kvasiregelbunden om sidorna växlar ges olika färger. I denna form är det ibland känt som tetratetraedern . De återstående konvexa reguljära polyedrarna har ett udda antal ytor vid varje vertex, så de kan inte färgas på ett sätt som bevarar kanttransitiviteten. Den har ett Coxeter-Dynkin-diagram

Var och en av dessa bildar den gemensamma kärnan av ett dubbelt par av vanliga polyedrar . Namnen på två av dessa ger ledtrådar till det associerade dubbla paret: respektive kub $\cap$ octahedron , respektive icosahedron $\cap$ dodecahedron . Oktaedern är den gemensamma kärnan av ett dubbelt par av tetraedrar (en förening som är känd som stella octangula ) ; när den härleds på detta sätt kallas oktaedern ibland tetratetraedern , som tetraeder $\cap$ tetraeder .

Regelbunden	Dubbel ordinarie	Kvasiregelbunden gemensam kärna	Vertex figur
Tetraeder {3,3} 3 | 2 3	Tetraeder {3,3} 3 | 2 3	Tetratetraeder r{3,3} 2 | 3 3	3.3.3.3
Kub {4,3} 3 | 2 4	Oktaeder {3,4} 4 | 2 3	Cuboctahedron r{3,4} 2 | 3 4	3.4.3.4
Dodekaeder {5,3} 3 | 2 5	Icosahedron {3,5} 5 | 2 3	Icosidodecahedron r{3,5} 2 | 3 5	3.5.3.5

Var och en av dessa kvasireguljära polyedrar kan konstrueras genom en korrigeringsoperation på endera av de vanliga föräldern, trunkering av topparna helt, tills varje originalkant reduceras till sin mittpunkt.

Kvasiregelbundna plattor

Denna sekvens fortsätter som den trehexagonala plattsättningen , vertexfigur (3.6) ² - en kvasiregelbunden plattsättning baserad på den triangulära plattsättningen och den sexkantiga plattsättningen .

Regelbunden	Dubbel ordinarie	Kvasiregelbunden kombination	Vertex figur
Hexagonal plattsättning {6,3} 6 | 2 3	Triangulär plattsättning {3,6} 3 | 2 6	Trihexagonal plattsättning r{6,3} 2 | 3 6	(3.6) 2

Schackbrädesmönstret är en kvasiregelbunden färgning av den kvadratiska plattsättningen , vertexfigur (4.4 ² ) :

Regelbunden	Dubbel ordinarie	Kvasiregelbunden kombination	Vertex figur
{4,4} 4 | 2 4	{4,4} 4 | 2 4	r{4,4} 2 | 4 4	(4.4) 2

Den triangulära plattsättningen kan också betraktas som kvasiregelbunden, med tre uppsättningar alternerande trianglar vid varje vertex, (3.3) ³ :

h{6,3} 3 | 3 3 =

I det hyperboliska planet fortsätter denna sekvens ytterligare, till exempel den triheptagonala plattsättningen , vertexfigur (3.7) ² - en kvasiregelbunden plattsättning baserad på ordningen-7 triangulär plattsättning och heptagonal plattsättning .

Regelbunden	Dubbel ordinarie	Kvasiregelbunden kombination	Vertex figur
Heptagonal plattsättning {7,3} 7 | 2 3	Triangulär plattsättning {3,7} 3 | 2 7	Triheptagonal plattsättning r{3,7} 2 | 3 7	(3.7) 2

Icke-konvexa exempel

Coxeter, HSM et al. (1954) klassificerar också vissa stjärnpolyedrar , som har samma egenskaper, som kvasiregelbundna.

Två är baserade på dubbla par av vanliga Kepler-Poinsot fasta ämnen , på samma sätt som för de konvexa exemplen:

den stora icosidodecahedron ${\begin{Bmatrix}3\\5/2\end{Bmatrix}}$ och dodecadodecahedron ${\begin{Bmatrix} 5\\5/2\end{Bmatrix}}$ :

Regelbunden	Dubbel ordinarie	Kvasiregelbunden gemensam kärna	Vertex figur
Stor stjärnformad dodekaeder { 5 / 2 ,3} 3 | 2 5/2	Stor ikosaeder {3, 5 / 2 } 5/2 | 2 3	Stor icosidodecahedron r{3, 5 / 2 } 2 | 3 5/2	3. 5 / 2 .3. 5/2 _ _
Liten stjärnformad dodekaeder { 5 / 2 ,5} 5 | 2 5/2	Stor dodekaeder {5, 5 / 2 } 5/2 | 2 5	Dodecadodecahedron r{5, 5 / 2 } 2 | 5 5/2	5. 5 / 2 .5. 5/2 _ _

Nio till är hemipolyedrarna , som är fasetterade former av de ovannämnda kvasireguljära polyedrarna som härrör från rektifiering av vanliga polyedrar. Dessa inkluderar ekvatoriska ytor som passerar genom mitten av polyedrarna:

Kvasireguljär (korrigerad)	Tetratetraeder	Cuboctahedron	Icosidodecahedron	Stor icosidodecahedron	Dodecadodecahedron
Kvasiregelbunden (hemipolyedra)	Tetrahemihexahedron 3 / 2 3 | 2	Octahemioctahedron 3 / 2 3 | 3	Liten icosihemidodecahedron 3 / 2 3 | 5	Great icosihemidodecahedron 3 / 2 3 | 5/3 _ _	Liten dodecahemicosahedron 5 / 3 5 / 2 | 3
Vertex figur	3.4. 3/2 .4 _ _	3.6. 3/2 .6 _ _	3.10. 3/2 .10 _ _	3. 10/3 . _ _ 3/2 . _ _ 10/3 _ _	5/2 .6 . _ 5/3 .6 _ _
Kvasiregelbunden (hemipolyedra)		Kubohemioctahedron 4 / 3 4 | 3	Liten dodekahemidodekaeder 5 / 4 5 | 5	Stor dodecahemidodecahedron 5 / 3 5 / 2 | 5/3 _ _	Great dodecahemicosahedron 5 / 4 5 | 3
Vertex figur		4.6. 4/3 .6 _ _	5.10. 5/4 .10 _ _	5/2 . _ _ 10/3 . _ _ 5/3 . _ _ 10/3 _ _	5.6. 5/4 .6 _ _

Slutligen finns det tre ditrigonala former, alla fasetteringar av den vanliga dodekaedern, vars vertexfigurer innehåller tre alternationer av de två ansiktstyperna:

Bild	Facetterad form Wythoff symbol Coxeter diagram	Vertex figur
	Ditrigonal dodecadodecahedron 3 | 5/3 5 eller	(5,5/3) 3
	Liten ditrigonal icosidodecahedron 3 | 5/2 3 eller	(3,5/2) 3
	Stor ditrigonal icosidodecahedron 3/2 | 3 5 eller	((3.5) 3 )/2

I det euklidiska planet fortsätter sekvensen av hemipolyedrar med följande fyra stjärnplattor, där apeirogoner visas som de tidigare nämnda ekvatorialpolygonerna:

Original rättad plattsättning	Kantdiagram _	Fast	Vertex Config	Wythoff	Symmetrigrupp
Fyrkantig plattsättning			4.∞.4/3.∞ 4.∞.-4.∞	4/3 4 | ∞	p4m
Triangulär kakel			(3.∞.3.∞.3.∞)/2	3/2 | 3 ∞	p6m
Tresexkantigt kakel			6.∞.6/5.∞ 6.∞.-6.∞	6/5 6 | ∞
			∞.3.∞.3/2 ∞.3.∞.-3	3/2 3 | ∞

Kvasireguljära dualer

Vissa myndigheter hävdar att eftersom dualerna av de kvasiregulära soliderna delar samma symmetri, bör dessa dualer också kallas kvasiregulära. Men alla använder inte denna terminologi. Dessa dualer är transitiva på sina kanter och ytor (men inte på sina hörn); de är kanttransitiva katalanska fasta ämnen . De konvexa är, i motsvarande ordning som ovan:

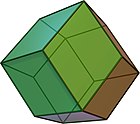
1. Den rombiska dodekaedern , med två typer av alternerande hörn, 8 med tre rombiska ansikten och 6 med fyra rombiska ansikten.
2. Den rombiska triakontaedern , med två typer av alternerande hörn, 20 med tre rombiska ansikten och 12 med fem rombiska ansikten.

Dessutom, genom dualitet med oktaedern, kan kuben , som vanligtvis är regelbunden , göras kvasiregelbunden om alternativa hörn ges olika färg.

Deras ansiktskonfigurationer är av formen V3.n.3.n och Coxeter-Dynkin-diagrammet

Kub V(3.3) 2	Rombisk dodekaeder V(3.4) 2	Rombisk triakontaeder V(3.5) 2	Rhombille plattsättning V(3.6) 2	V(3,7) 2	V(3,8) 2

Dessa tre kvasiregelbundna dualer kännetecknas också av att de har rombiska ansikten.

Detta rhombic-faced mönster fortsätter som V(3.6) ² , rhombille plattsättningen .

Kvasiregelbundna polytoper och bikakor

I högre dimensioner definierade Coxeter en kvasiregelbunden polytop eller honeycomb för att ha regelbundna fasetter och kvasiregelbundna vertexfigurer. Av detta följer att alla vertexfigurer är kongruenta och att det finns två sorters fasetter, som alternerar.

- rum kan den vanliga 16-cellen också ses som kvasireguljär som en alternerad tesserakt , h{4,3,3}, Coxeter-diagram : = , sammansatt av alternerande tetraeder- och tetraederceller . Dess vertexfigur är den kvasiregelbundna tetratetraedern (en oktaeder med tetraedrisk symmetri), .

Den enda kvasireguljära bikakan i euklidisk 3-rymden är den alternerade kubiska bikakan , h{4,3,4}, Coxeter-diagram: = , sammansatt av alternerande tetraedriska och oktaedriska celler . Dess vertexfigur är den kvasiregelbundna kuboktaedern , .

I hyperboliskt 3-rum är en kvasiregelbunden bikaka den alternerade ordningen-5 kubiska bikakan , h{4,3,5}, Coxeter-diagram: = , sammansatt av alternerande tetraedriska och icosaedriska celler . Dess vertexfigur är den kvasiregelbundna icosidodecahedronen , . En relaterad parakompakt alternerad ordning-6 kubisk honeycomb , h{4,3,6} har alternerande tetraedriska och hexagonala kakelceller med vertexfigur är en kvasiregelbunden trihexagonal plattsättning , .

Kvasiregelbunden polychora och honeycombs: h{4,p,q}
Plats	Ändlig	Affine	Kompakt	Paracompact
Schläfli symbol	h{4,3,3}	h{4,3,4}	h{4,3,5}	h{4,3,6}	h{4,4,3}	h{4,4,4}
	$\left\{3,{3 \atop 3}\right\}$	$\left\{3,{4 \atop 3}\right\}$	$\left\{3,{5 \atop 3}\right\}$	$\left\{3,{6 \atop 3}\right\}$	$\left\{4,{4 \atop 3}\right\}$	$\left\{4,{4 \atop 4}\right\}$
Coxeter diagram	↔	↔	↔	↔	↔	↔
	↔					↔
Bild
Vertex figur r{p,3}

Vanliga polychora eller honungskakor av formen {p,3,4} eller kan ha sin symmetri halverad som i kvasiregelbunden form , vilket skapar växelvis färgade {p,3} celler. Dessa fall inkluderar den euklidiska kubiska bikakan {4,3,4} med kubiska celler, och kompakt hyperbolisk {5,3,4} med dodekaedriska celler, och parakompakt {6,3,4} med oändliga hexagonala kakelceller . De har fyra celler runt varje kant, omväxlande i 2 färger. Deras vertexfigurer är kvasiregelbundna tetratetraedrar, = .

Vanlig vertexfigur är den kvasiregelbundna tetratetraedern, , samma som vanlig oktaeder

Regelbundna och kvasiregelbundna bikakor: {p,3,4} och {p,3 1,1 }
Plats	Euklidiskt 4-utrymme	Euklidiskt 3-utrymme	Hyperboliskt 3-mellanslag
namn	{3,3,4} {3,3 1,1 } = $\left\{3,{3 \atop 3}\right\}$	{4,3,4} {4,3 1,1 } = $\left\{4,{3 \atop 3}\right\}$	{5,3,4} {5,3 1,1 } = $\left\{5,{3 \atop 3}\right\}$	{6,3,4} {6,3 1,1 } = $\left\{6,{3 \atop 3}\right\}$
Coxeter diagram	=	=	=	=
Bildceller {s
, 3}

Liknande regelbundna hyperboliska bikakor av formen {p,3,6} eller kan ha sin symmetri halverad som i kvasiregelbunden form , vilket skapar växelvis färgade {p,3} celler. De har sex celler runt varje kant, omväxlande i två färger. Deras vertexfigurer är kvasiregelbundna triangulära plattor , .

Den gemensamma vertexfiguren är en kvasiregelbunden triangulär plattsättning , =

Hyperboliska enhetliga bikakor : {p,3,6} och {p,3 ^[3] }

Form	Paracompact				Icke-kompakt
namn	{3,3,6} {3,3 [3] }	{4,3,6} {4,3 [3] }	{5,3,6} {5,3 [3] }	{6,3,6} {6,3 [3] }	{7,3,6} {7,3 [3] }	{8,3,6} {8,3 [3] }	... {∞,3,6} {∞,3 [3] }
Bild
Celler	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

Se även

• Kiral polytop
• Rättning (geometri)

Anteckningar

• Cromwell, P. Polyhedra , Cambridge University Press (1977).
•   Coxeter , Regular Polytopes , (3:e upplagan, 1973), Dover-upplagan, ISBN 0-486-61480-8 , 2.3 Quasi-Regular Polyhedra. (s. 17), Quasi-regular honeycombs s.69

externa länkar

• Weisstein, Eric W. "Quasiregular polyhedron" . MathWorld .
• Weisstein, Eric W. "Uniform polyhedron" . MathWorld . Kvasireguljära polyedrar: (pq) ^r
• George Hart, kvasiregulära polyedrar