Rhombicosidodecahedron
| Rhombicosidodecahedron | |
|---|---|
 (Klicka här för roterande modell) |
|
| Typ |
Arkimedesk solid Uniform polyeder |
| Element | F = 62, E = 120, V = 60 (χ = 2) |
| Ansikten vid sida | 20{3}+30{4}+12{5} |
| Conway notation | eD eller aaD |
| Schläfli symboler | rr{5,3} eller |
| t 0,2 {5,3} | |
| Wythoff symbol | 3 5 | 2 |
| Coxeter diagram |
|
| Symmetrigrupp | Ih , , H3 , [5,3] (*532), ordning 120 |
| Rotationsgrupp | I , [5,3] + , (532), order 60 |
| Dihedral vinkel |
3-4: 159°05′41″ (159,09°) 4-5: 148°16′57″ (148,28°) |
| Referenser | U27 , C30 , W14 _ _ _ |
| Egenskaper | Halvregelbunden konvex |
 Färgade ansikten |
 3.4.5.4 ( Vertex figur ) |
 Deltoidal hexecontahedron ( dubbel polyeder ) |
 Netto |
Inom geometrin är rhombicosidodecahedron , eller Rectified Rhombic Triacontahedron , en arkimedisk fast substans , en av tretton konvexa isogonala ickeprismatiska solider konstruerade av två eller flera typer av regelbundna polygonytor .
Den har 20 vanliga triangulära ytor, 30 fyrkantiga ytor, 12 vanliga femkantiga ytor, 60 hörn och 120 kanter .
Namn
Johannes Kepler i Harmonices Mundi (1618) kallade denna polyeder en rhombicosidodecahedron , vilket är en förkortning för trunkerad icosidodecahedral rhombus , med icosidodecahedral rhombus som hans namn för en rhombic triacontahedron . Det finns olika avkortningar av en rombisk triacontahedron till en topologisk rombicosidodekaeder: Framträdande dess rätning (vänster), den som skapar det enhetliga fasta ämnet (mitten) och rätningen av den dubbla icosidodekaedern (höger), som är kärnan i den dubbla föreningen .
Det kan också kallas en expanderad eller kantellerad dodekaeder eller icosahedron, från trunkeringsoperationer på antingen enhetlig polyeder .
Mått
För en rhombicosidodecahedron med kantlängd a är dess yta och volym:
Geometriska relationer
Om du expanderar en ikosaeder genom att flytta ansikten bort från ursprunget i rätt mängd, utan att ändra orienteringen eller storleken på ansikten, eller gör samma sak med dess dubbla dodekaeder och lappar de fyrkantiga hålen i resultatet, får du en rhombicosidodecahedron. Därför har den samma antal trianglar som en ikosaeder och samma antal femhörningar som en dodekaeder, med en kvadrat för varje kant av båda.
Alternativt, om du expanderar var och en av fem kuber genom att flytta ytorna bort från origo rätt mycket och rotera var och en av de fem 72° runt så att de är lika långt från varandra, utan att ändra orienteringen eller storleken på ytorna, och lappa femkantiga och triangulära hål i resultatet får du en rhombicosidodecahedron. Därför har den samma antal rutor som fem kuber.
Två klungor av ansikten av bilunabirotunda , lunorna (varje lune har två trianglar intill motsatta sidor av en kvadrat), kan riktas in med en kongruent fläck av ansikten på rhombicosidodecahedron . Om två bilunabirotundae är inriktade på detta sätt på motsatta sidor av rhombicosidodecahedron, kan en kub placeras mellan bilunabirotundae i mitten av rhombicosidodecahedron.
Den rhombicosidodecahedron delar vertexarrangemanget med den lilla stjärnformade trunkerade dodekaedern och med de enhetliga sammansättningarna av sex eller tolv pentagrammiska prismor .
Zometool - satserna för att göra geodetiska kupoler och andra polyedrar använder slitsade kulor som kopplingar. Kulorna är "expanderade" rhombicosidodecahedra, med rutorna ersatta av rektanglar. Expansionen är vald så att de resulterande rektanglarna är gyllene rektanglar .
Tolv av de 92 Johnson-fastämnena härleds från rhombicosidodecahedron, fyra av dem genom rotation av en eller flera femkantiga kupoler : gyrat- , parabigyrat- , metabigyrat- och trigyratrhombicosidodecahedron . Åtta till kan konstrueras genom att ta bort upp till tre kupoler, ibland också rotera en eller flera av de andra kupolerna.
kartesiska koordinater
Kartesiska koordinater för hörn av en rhombicosidodecahedron med en kantlängd på 2 centrerad vid origo är alla jämna permutationer av:
- (±1, ±1, ± φ 3 ),
- (± φ 2 , ± φ , ±2 φ ),
- (±(2+ φ ), 0, ± φ 2 ),
där φ = 1 + 5/2 är gyllene . √ det snittet Därför är omkretsradien för denna rhombicosidodecahedron det gemensamma avståndet för dessa punkter från origo, nämligen √ φ 6 +2 = √ 8φ+7 för kantlängd 2. För enhetskantlängd måste R halveras, vilket ger
- R = √ 8 φ +7 / 2 = √ 11+4 √ 5 / 2 ≈ 2,233.
Ortogonala projektioner
Den rhombicosidodecahedron har sex speciella ortogonala projektioner , centrerade, på en vertex, på två typer av kanter och tre typer av ytor: trianglar, kvadrater och femhörningar. De två sista motsvarar A 2 - och H 2 Coxeter - planen .
| Centrerad av | Vertex |
Kant 3-4 |
Kant 5-4 |
Face Square |
Ansiktstriangel _ |
Ansikte Pentagon |
|---|---|---|---|---|---|---|
| Solid |

|

|

|
|||
| trådram |

|

|

|

|

|

|
|
Projektiv symmetri |
[2] | [2] | [2] | [2] | [6] | [10] |
|
Dubbel bild |

|

|

|

|

|

|
Sfärisk plattsättning
Den rhombicosidodecahedron kan också representeras som en sfärisk plattsättning och projiceras på planet via en stereografisk projektion . Denna projektion är konform och bevarar vinklar men inte ytor eller längder. Raka linjer på sfären projiceras som cirkelbågar på planet.

|
 Pentagon -centrerad |
 Triangelcentrerad _ |
 Fyrkantigt centrerad |
| Ortografisk projektion | Stereografiska projektioner | ||
|---|---|---|---|
Besläktade polyedrar
| Familj av enhetliga icosaedriska polyedrar | |||||||
|---|---|---|---|---|---|---|---|
| Symmetri : [5,3] , (*532) | [5,3] + , (532) | ||||||

|

|

|

|

|

|

|

|
|
|
|
|
|
|
|
|
|
| {5,3} | t{5,3} | r{5,3} | t{3,5} | {3,5} | rr{5,3} | tr{5,3} | sr{5,3} |
| Dual till enhetliga polyedrar | |||||||
|
|

|

|

|
|
|

|

|
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
Symmetrimutationer
Denna polyeder är topologiskt relaterad som en del av en sekvens av kantellerade polyedrar med vertexfigur (3.4.n.4), som fortsätter som plattsättningar av det hyperboliska planet . Dessa vertextransitiva figurer har (*n32) reflektionssymmetri .
| * n 32 symmetrimutation av expanderade plattsättningar: 3.4. n .4 | ||||||||
|---|---|---|---|---|---|---|---|---|
|
Symmetri * n 32 [n,3] |
Sfärisk | Euklid. | Kompakt hyperb. | Paracomp. | ||||
|
*232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] |
|
| Figur |
|

|

|

|

|

|

|

|
| Konfig. | 3.4.2.4 | 3.4.3.4 | 3.4.4.4 | 3.4.5.4 | 3.4.6.4 | 3.4.7.4 | 3.4.8.4 | 3.4.∞.4 |
Johnson fasta ämnen
Det finns 12 relaterade Johnson-fastämnen , 5 genom förminskning och 8 inklusive gyrationer:
J5
|
76
|
80
|
81
|
83
|
72
|
73
|
74
|
75
|
77
|
78
|
79
|
82
|
Vertex arrangemang
Den rhombicosidodecahedron delar sitt vertexarrangemang med tre icke-konvexa enhetliga polyedrar : den lilla stjärnformade trunkerade dodecahedronen , den lilla dodecicosidodecahedronen (som har de triangulära och femkantiga ytorna gemensamt) och den lilla rhombidodecahedronen (som har de fyrkantiga ytorna gemensamt).
Den delar också sitt vertexarrangemang med de enhetliga sammansättningarna av sex eller tolv pentagrammiska prismor .
Rhombicosidodecahedral graf
| Rhombicosidodecahedral graf | |
|---|---|
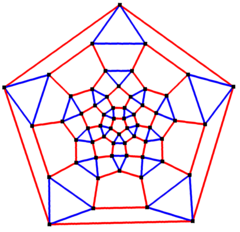 Pentagon centrerad Schlegel-diagram
| |
| Vertices | 60 |
| Kanter | 120 |
| Automorfismer | 120 |
| Egenskaper | Kvartisk graf , Hamiltonian , regelbunden |
| Tabell över grafer och parametrar | |
Inom det matematiska området för grafteorin är en rhombicosidodecahedral graf grafen över hörn och kanter av rhombicosidodecahedron, en av arkimediska fasta ämnen . Den har 60 hörn och 120 kanter och är en kvartsgraf Arkimedeansk graf .

Se även
Anteckningar
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design . Dover Publications, Inc. ISBN 0-486-23729-X . (Avsnitt 3-9)
- Cromwell, P. (1997). Polyeder . Storbritannien: Cambridge. s. 79–86 Arkimedeiska fasta ämnen . ISBN 0-521-55432-2 .
- The Big Bang Theory Series 8 Episod 2 - The Junior Professor Solution : innehåller denna solida lösning som svaret på ett improviserat vetenskapsquiz som de fyra huvudkaraktärerna har i Leonards och Sheldons lägenhet, och illustreras även i Chuck Lorres Vanity Card #461 på slutet av det avsnittet.
externa länkar
- Eric W. Weisstein , Small Rhombicosidodecahedron ( Arkimedean solid) på MathWorld .
- Klitzing, Richard. "3D konvexa likformiga polyedrar x3o5x - srid" .
- Redigerbart utskrivbart nät av en Rhombicosidodecahedron med interaktiv 3D-vy
- Den enhetliga polyedern
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra







































































