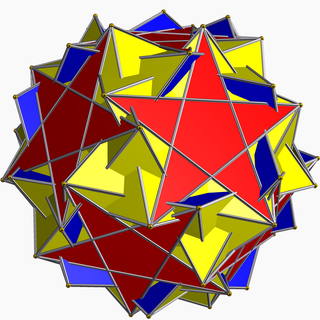
Inverterad snub dodecadodecahedron

Inverterad snub dodecadodecahedron

Typ	Uniform stjärnpolyeder
Element	F = 84, E = 150 V = 60 (χ = -6)
Ansikten vid sida	60{3}+12{5}+12{5/2}
Coxeter diagram
Wythoff symbol	\| 5/3 2 5
Symmetrigrupp	I, [5,3] ⁺ , 532
Indexreferenser	U ₆₀ , C ₇₆ , W ₁₁₄
Dubbel polyeder	Medial inverterad femkantig hexecontahedron
Vertex figur	3.3.5.3.5/3
Bowers förkortning	Isdid

3D-modell av en inverterad snub dodecadodecahedron

Inom geometri är den inverterade snubben dodecadodecahedron (eller vertisnub dodecadodecahedron ) en icke-konvex enhetlig polyhedron, indexerad som U ₆₀ . Den får en Schläfli-symbol sr{5/3,5}.

kartesiska koordinater

Kartesiska koordinater för hörn av en inverterad snub dodecadodecahedron är alla jämna permutationer av

(±2α, ±2, ±2β),

(±(α+β/τ+τ), ±(-ατ+β+1/τ), ±(α/τ+βτ-1)), (±

( -α/τ+βτ+1), ±(-α+β/τ-τ), ±(ατ+β-1/τ)), (±(-α/

τ+βτ-1), ±(α -β/τ-τ), ±(ατ+β+1/τ)) och

(±(α+β/τ-τ), ±(ατ-β+1/τ), ±(α/τ+βτ +1)),

med ett jämnt antal plustecken, där

β = (α ² /τ+τ)/(ατ−1/τ),

där τ = (1+ √ 5 )/2 är det gyllene medelvärdet och α är den negativa reella roten av τα ⁴ −α ³ +2α ² −α−1/τ, eller ungefär −0,3352090. Att ta de udda permutationerna av ovanstående koordinater med ett udda antal plustecken ger en annan form, enantiomorfen av den andra.

Besläktade polyedrar

Medial inverterad femkantig hexecontahedron

Medial inverterad femkantig hexecontahedron

Typ	Stjärnpolyeder
Ansikte
Element	F = 60, E = 150 V = 84 (χ = -6)
Symmetrigrupp	I, [5,3] ⁺ , 532
Indexreferenser	DU ₆₀
dubbel polyeder	Inverterad snub dodecadodecahedron

3D-modell av en medial inverterad femkantig hexecontahedron

Den mediala inverterade femkantiga hexecontahedronen (eller midly petaloid ditriacontahedron ) är en nonconvex isohedral polyhedron . Det är dual av den enhetliga inverterade snubbade dodecadodekaedern. Dess ansikten är oregelbundna icke-konvexa femhörningar, med en mycket spetsig vinkel.

Proportioner

Beteckna det gyllene snittet med $\phi$ , och låt $\xi \approx -0,236\,993\,843\,45$ vara den största (minst negativa) reella nollan av polynomet $P=8x^{4}-12x^{3}+5x+1$ . Sedan har varje yta tre lika stora vinklar av ${\displaystyle \arccos(\xi )\approx 103.709\,182\,219\,53^{\circ }arccos,$ $\arccos(\phi ^{2}\xi +\phi )\approx 3.990\,130\,423\,41^{\circ }$ av och en av $360^{\circ }\-\arccos(\xi ^{-2} {-1})\approx 224.882\,322\,917\,99^{\circ }$ . Varje ansikte har en medellång kant, två korta och två långa. Om medellängden är $2$ så har kortkanterna längd

1-{\sqrt {(1-\xi)/(\phi ^{3}-\xi )}}\approx 0,474\,126\,460\,54

,

och långkanterna har längd

1+{\sqrt {(1-\xi)/(-\phi ^{-3}-\xi ) }}\approx 37.551\,879\,448\,54

.

Den dihedriska vinkeln är lika med $\arccos(\xi /(\xi +1))\approx 108.095\^,5219,\ {\circ }$ . Den andra reella nollan i polynomet $P$ spelar en liknande roll för den mediala femkantiga hexekontaedern .

Se även

Wenninger, Magnus (1983), Dual Models , Cambridge University Press , ISBN 978-0-521-54325-5 , MR 0730208 sid. 124

externa länkar